library(ggplot2)
library(forecast)
library(fpp2)
library(plotly)Tema III: Técnicas de suavizamiento exponencial
Curso: Análisis de series temporales
1 librerías
2 Suavizamiento exponencial simple
2.1 Serie mensual de defunciones de Costa Rica de los años 2001 y 2002.
defunciones<-read.csv("defunciones.csv",sep=",")
y<-ts(defunciones$defunciones,start=c(2001,1),frequency=12)
autoplot(y) 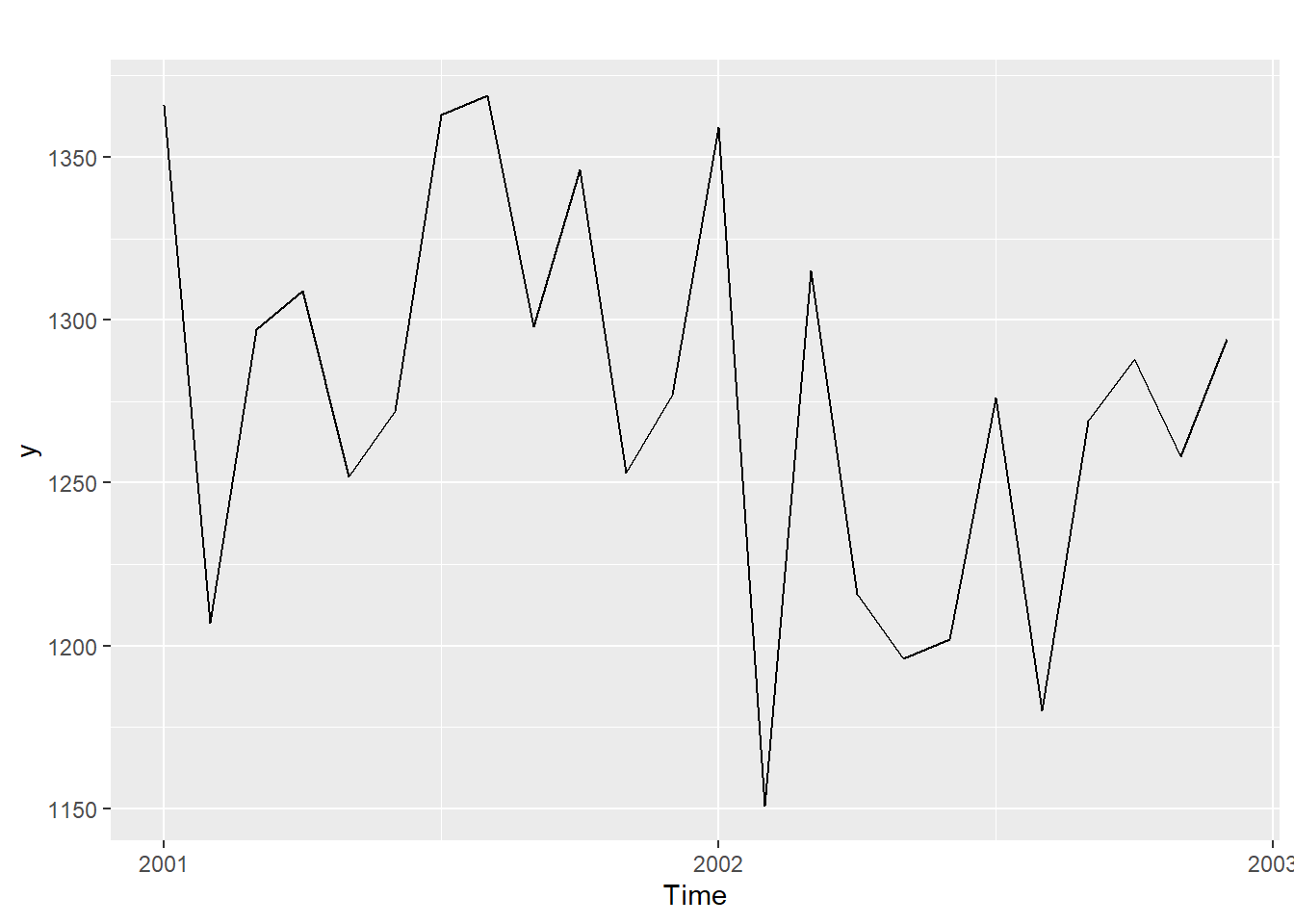
ses1 <- ses(y,alpha=0.3,initial="simple")
names(ses1) [1] "model" "mean" "level" "x" "upper" "lower"
[7] "fitted" "residuals" "method" "series" ses1$modelSimple exponential smoothing
Call:
ses(y = y, initial = "simple", alpha = 0.3)
Smoothing parameters:
alpha = 0.3
Initial states:
l = 1366
sigma: 65.314ses1$fitted #valores ajustados Jan Feb Mar Apr May Jun Jul Aug
2001 1366.000 1366.000 1318.300 1311.910 1311.037 1293.326 1286.928 1309.750
2002 1296.395 1315.176 1265.924 1280.646 1261.253 1241.677 1229.774 1243.642
Sep Oct Nov Dec
2001 1327.525 1318.667 1326.867 1304.707
2002 1224.549 1237.884 1252.919 1254.443ses1$residuals #residuos Jan Feb Mar Apr May Jun
2001 0.000000 -159.000000 -21.300000 -2.910000 -59.037000 -21.325900
2002 62.605099 -164.176430 49.076499 -64.646451 -65.252516 -39.676761
Jul Aug Sep Oct Nov Dec
2001 76.071870 59.250309 -29.524784 27.332651 -73.867144 -27.707001
2002 46.226267 -63.641613 44.450871 50.115610 5.080927 39.5566492.2 Estimación de alpha
alpha<-seq(0,1,0.01)
rmse<-as.numeric()
for(i in 1:length(alpha)){
ses1 <- ses(y,alpha=alpha[i],initial="simple")
rmse[i]<-accuracy(ses1)[2]
}
rmse [1] 108.60153 100.87503 94.51549 89.28806 84.99476 81.46960 78.57438
[8] 76.19476 74.23668 72.62315 71.29144 70.19051 69.27899 68.52330
[15] 67.89624 67.37573 66.94384 66.58597 66.29023 66.04692 65.84810
[22] 65.68727 65.55907 65.45913 65.38382 65.33017 65.29571 65.27840
[29] 65.27656 65.28880 65.31395 65.35105 65.39931 65.45805 65.52670
[36] 65.60482 65.69199 65.78788 65.89222 66.00475 66.12528 66.25362
[43] 66.38962 66.53312 66.68402 66.84221 67.00757 67.18002 67.35948
[50] 67.54586 67.73909 67.93911 68.14584 68.35923 68.57921 68.80573
[57] 69.03874 69.27817 69.52398 69.77612 70.03454 70.29920 70.57006
[64] 70.84707 71.13019 71.41939 71.71463 72.01588 72.32310 72.63627
[71] 72.95535 73.28033 73.61117 73.94786 74.29037 74.63869 74.99280
[78] 75.35269 75.71835 76.08977 76.46693 76.84985 77.23852 77.63294
[85] 78.03310 78.43903 78.85073 79.26821 79.69148 80.12057 80.55550
[92] 80.99628 81.44296 81.89555 82.35410 82.81865 83.28924 83.76592
[99] 84.24873 84.73774 85.23301plot(alpha,rmse,type = "l")
alpha[rmse==min(rmse)][1] 0.28abline(v=alpha[rmse==min(rmse)])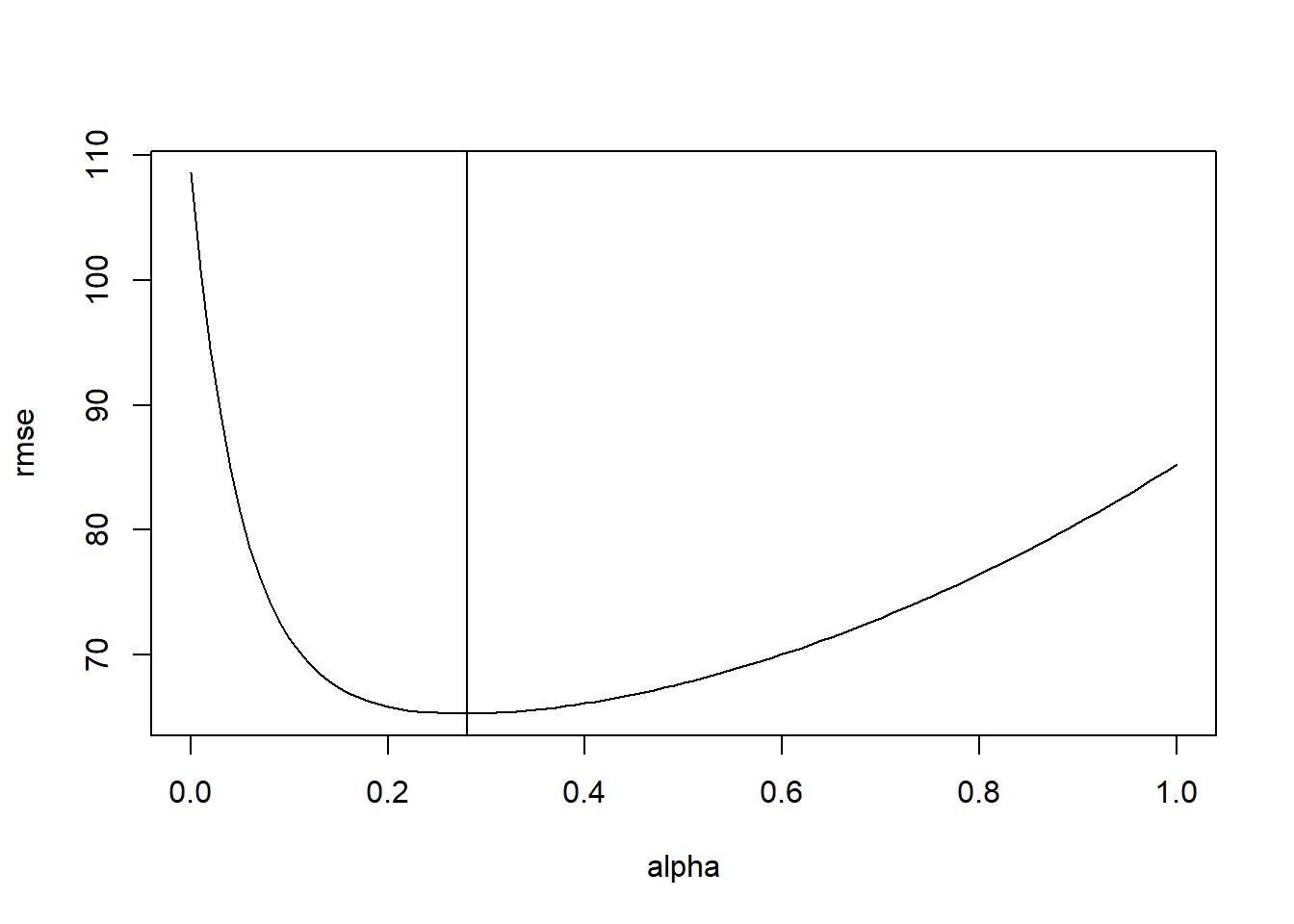
ses2 <- ses(y,h=12,initial="simple")
names(ses2) [1] "model" "mean" "level" "x" "upper" "lower"
[7] "fitted" "residuals" "method" "series" ses2$modelSimple exponential smoothing
Call:
ses(y = y, h = 12, initial = "simple")
Smoothing parameters:
alpha = 0.2762
Initial states:
l = 1366
sigma: 65.2755ses2 Point Forecast Lo 80 Hi 80 Lo 95 Hi 95
Jan 2003 1264.946 1181.292 1348.600 1137.008 1392.884
Feb 2003 1264.946 1178.159 1351.733 1132.217 1397.675
Mar 2003 1264.946 1175.136 1354.756 1127.594 1402.298
Apr 2003 1264.946 1172.211 1357.681 1123.120 1406.772
May 2003 1264.946 1169.376 1360.516 1118.784 1411.108
Jun 2003 1264.946 1166.622 1363.270 1114.573 1415.319
Jul 2003 1264.946 1163.944 1365.948 1110.476 1419.416
Aug 2003 1264.946 1161.334 1368.558 1106.485 1423.407
Sep 2003 1264.946 1158.789 1371.103 1102.593 1427.299
Oct 2003 1264.946 1156.303 1373.589 1098.791 1431.101
Nov 2003 1264.946 1153.873 1376.019 1095.075 1434.817
Dec 2003 1264.946 1151.495 1378.397 1091.438 1438.454autoplot(ses2)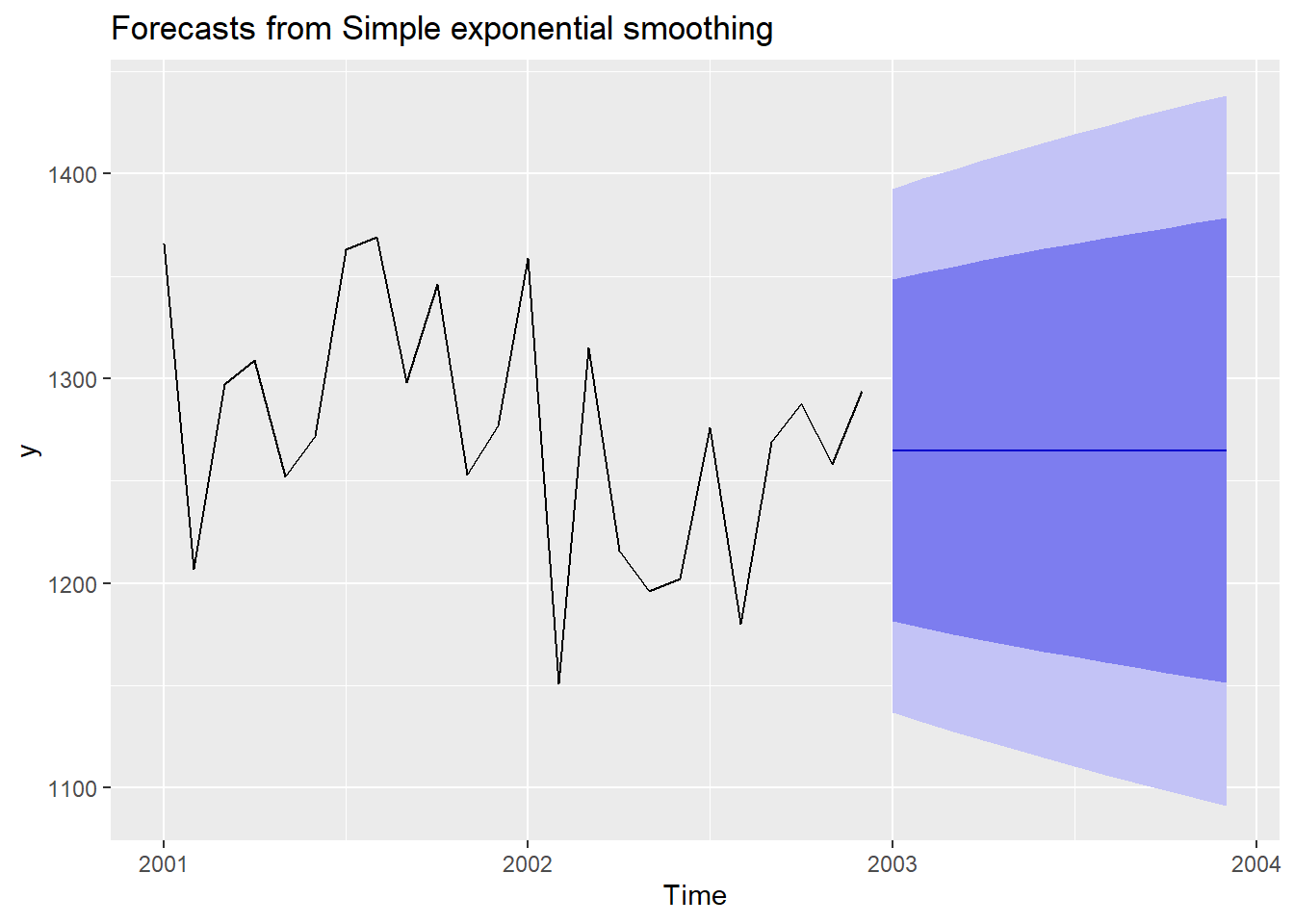
autoplot(ses2) +
autolayer(fitted(ses2), series="ajustado") +
ylab("defunciones") + xlab("mes")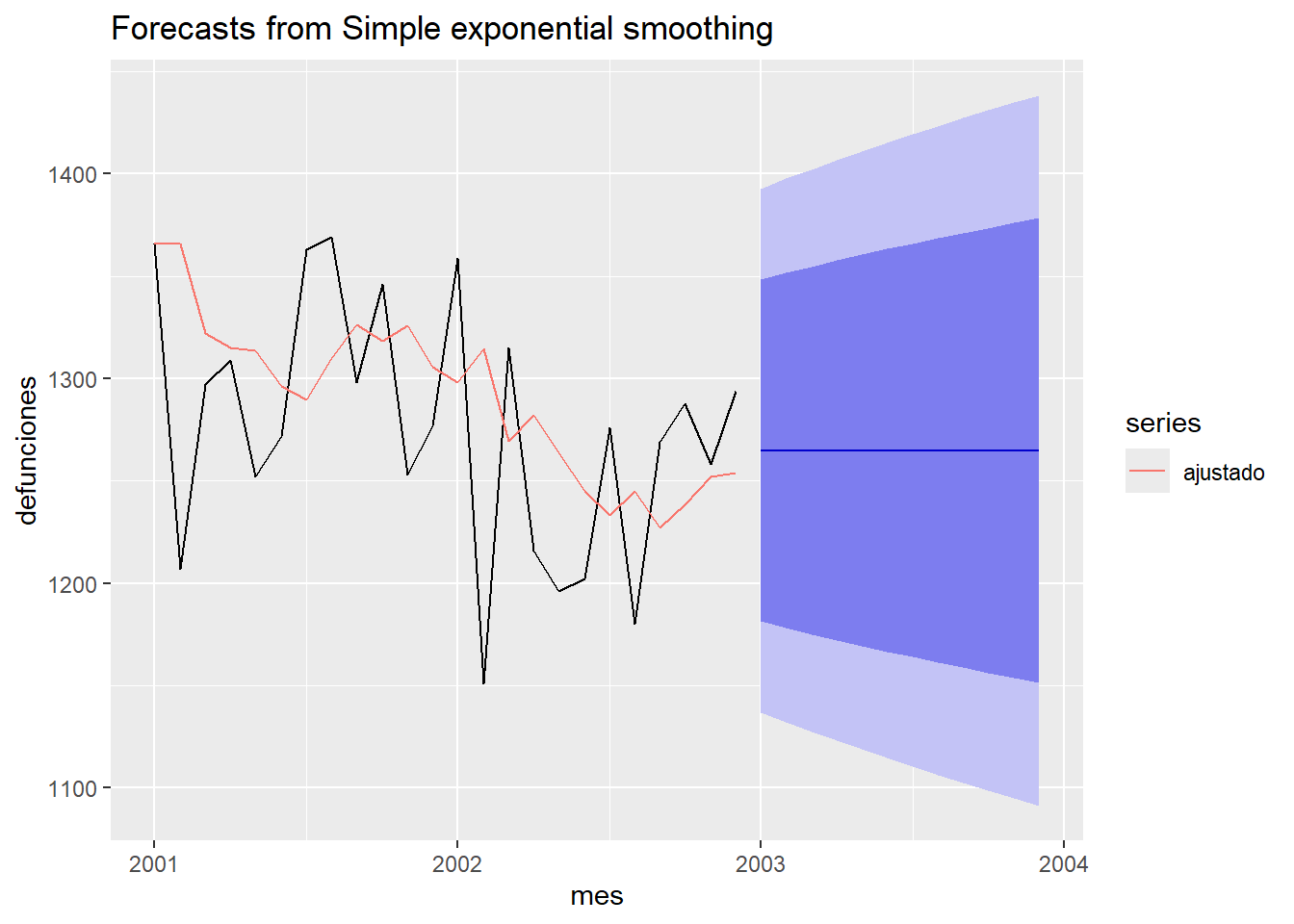
3 Método de Holt
3.1 Serie de graduados del ITCR de 1975-2002.
itcrgrad<-read.csv("ITCR.csv",sep=",")
y<-ts(itcrgrad$graduados,start=1975)
autoplot(y) 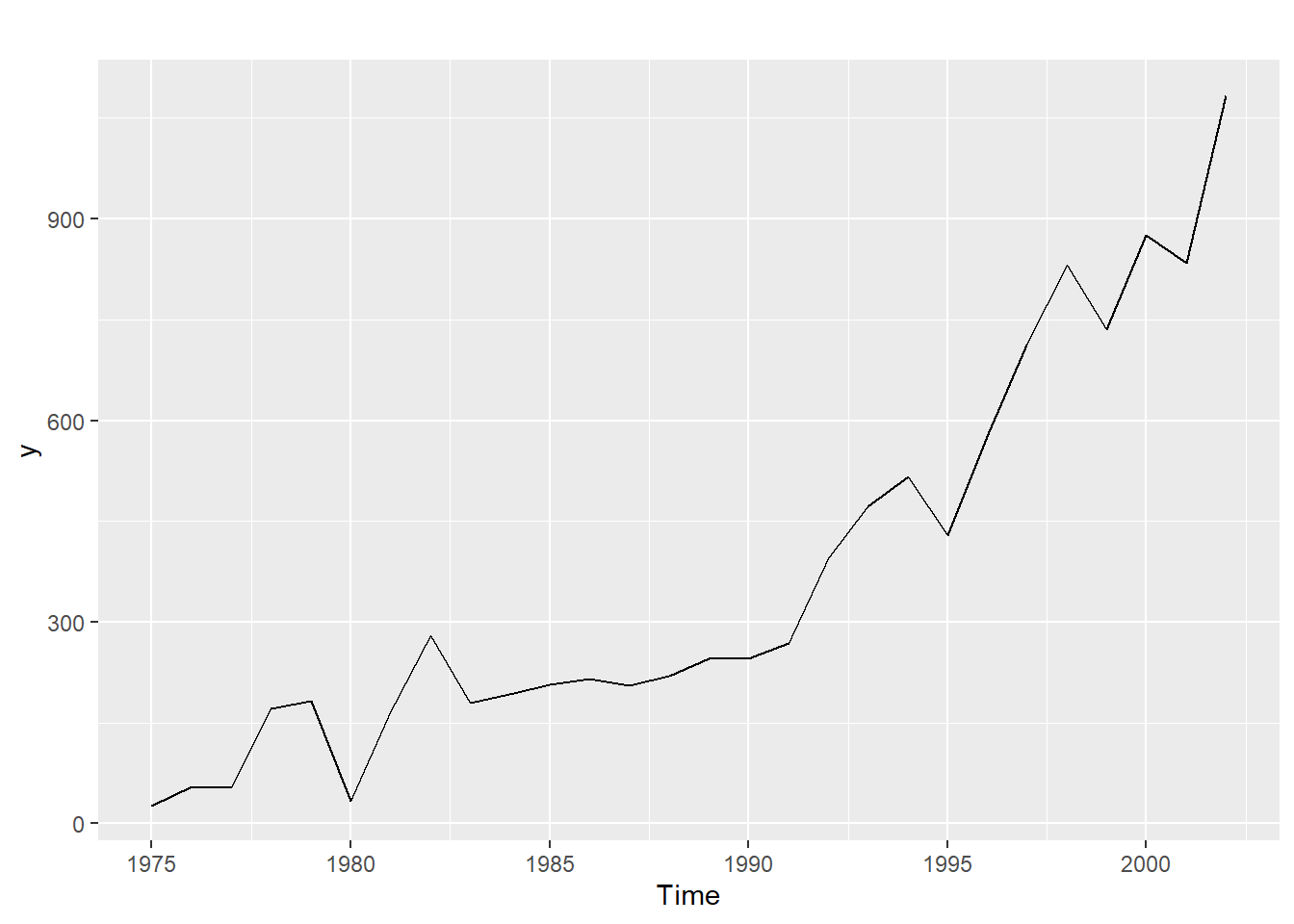
holt1 <- holt(y,alpha=0.3 ,beta=0.64 , h=5, initial="simple")
holt1 Point Forecast Lo 80 Hi 80 Lo 95 Hi 95
2003 1070.326 969.4715 1171.180 916.0824 1224.569
2004 1139.327 1000.9103 1277.744 927.6368 1351.018
2005 1208.329 997.2560 1419.401 885.5209 1531.136
2006 1277.330 969.6265 1585.033 806.7382 1747.922
2007 1346.331 924.5718 1768.091 701.3058 1991.357names(holt1) [1] "model" "mean" "level" "x" "upper" "lower"
[7] "fitted" "residuals" "method" "series" holt1$modelHolt's method
Call:
holt(y = y, h = 5, initial = "simple", alpha = 0.3, beta = 0.64)
Smoothing parameters:
alpha = 0.3
beta = 0.64
Initial states:
l = 27
b = 28
sigma: 78.6971holt1$mean # pronóstico con 5 pasos para adelante.Time Series:
Start = 2003
End = 2007
Frequency = 1
[1] 1070.326 1139.327 1208.329 1277.330 1346.331holt1$x # serie originalTime Series:
Start = 1975
End = 2002
Frequency = 1
[1] 27 55 54 171 182 34 165 280 179 192 207 216 205 220 245
[16] 245 269 394 472 516 429 576 713 832 735 876 834 1084holt1$fitted # valores ajustadosTime Series:
Start = 1975
End = 2002
Frequency = 1
[1] 55.00000 69.22400 84.84979 89.56469 143.60069 192.09856 151.29215
[8] 164.65957 230.66212 236.64478 236.16085 234.72321 232.82201 222.84934
[15] 219.82140 230.03613 240.05951 259.83245 336.93367 440.23727 540.29623
[22] 562.86862 625.29053 726.92608 853.94515 890.92104 956.23932 965.89217holt2 <- holt(y , h=5, initial="simple")
holt2 Point Forecast Lo 80 Hi 80 Lo 95 Hi 95
2003 1032.582 924.7634 1140.401 867.6875 1197.477
2004 1060.582 933.8395 1187.325 866.7459 1254.419
2005 1088.582 945.3952 1231.770 869.5964 1307.568
2006 1116.582 958.6539 1274.511 875.0516 1358.113
2007 1144.582 973.1758 1315.989 882.4386 1406.726names(holt2) [1] "model" "mean" "level" "x" "upper" "lower"
[7] "fitted" "residuals" "method" "series" holt2$modelHolt's method
Call:
holt(y = y, h = 5, initial = "simple")
Smoothing parameters:
alpha = 0.6179
beta = 0
Initial states:
l = 27
b = 28
sigma: 84.1316cbind(y,holt2$fitted)Time Series:
Start = 1975
End = 2002
Frequency = 1
y holt2$fitted
1975 27 55.00000
1976 55 65.69798
1977 54 87.08739
1978 171 94.64173
1979 182 169.82573
1980 34 205.34857
1981 165 127.46729
1982 280 178.65985
1983 179 269.28088
1984 192 241.49369
1985 207 238.91010
1986 216 247.19192
1987 205 255.91752
1988 220 252.45410
1989 245 260.39977
1990 245 278.88380
1991 269 285.94601
1992 394 303.47458
1993 472 387.41287
1994 516 467.68172
1995 429 525.53899
1996 576 493.88474
1997 713 572.62615
1998 832 687.36724
1999 735 804.74004
2000 876 789.64564
2001 834 871.00651
2002 1084 876.13911autoplot(holt2) +
autolayer(fitted(holt2), series="ajustado") +
ylab("defunciones") + xlab("mes")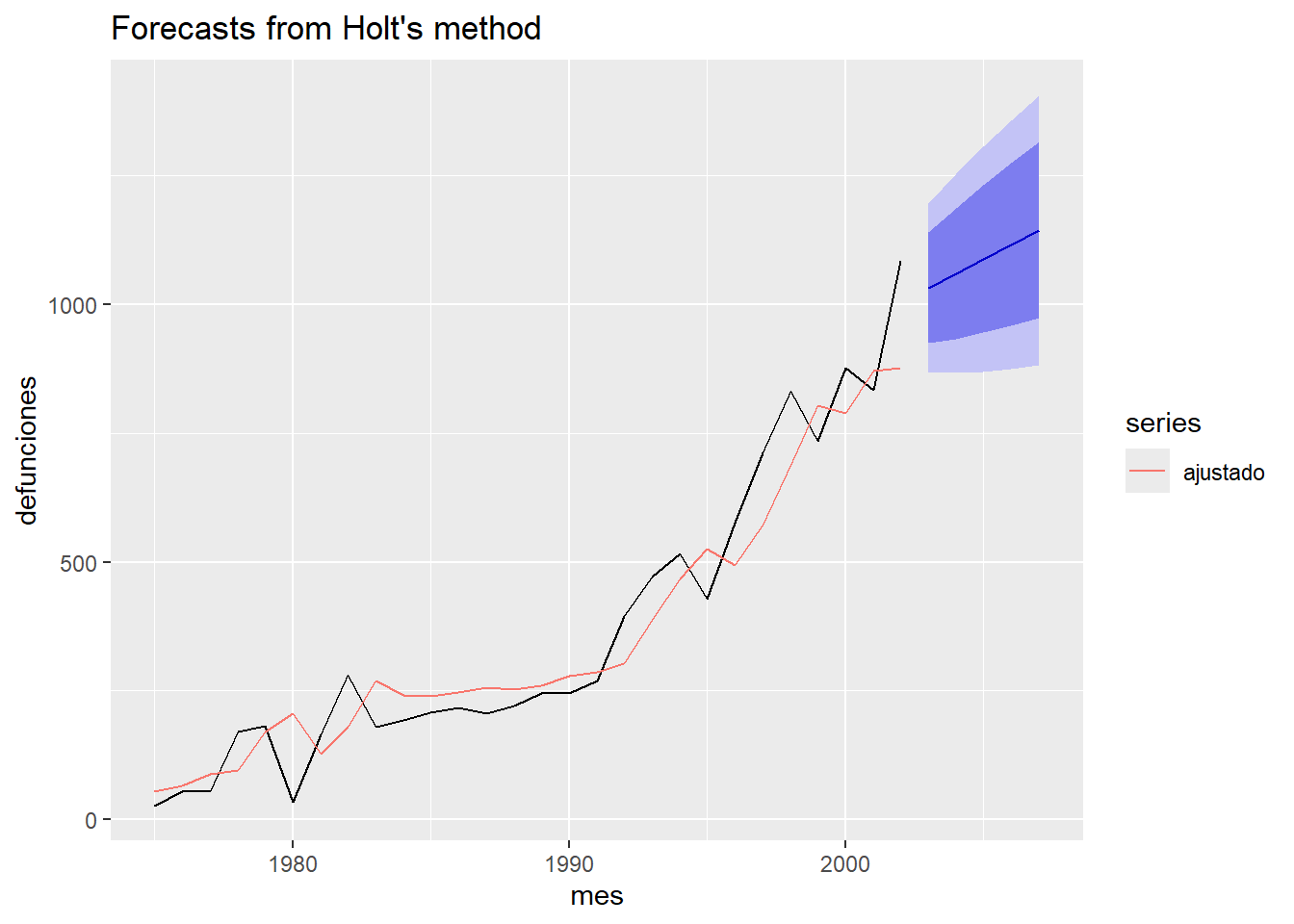
3.2 Estimación de alpha y beta
alpha<-seq(0,1,0.01)
beta<-seq(0,1,0.01)
rmse<-matrix(NA,nrow=length(alpha),ncol=length(beta))
for(i in 1:length(alpha)){
for(j in 1:length(beta)){
ses1 <- holt(y,alpha=alpha[i],beta=beta[j],initial="simple")
rmse[i,j]<-accuracy(ses1)[2]
}
}
dim(rmse)[1] 101 101rmse[1:5,1:5] [,1] [,2] [,3] [,4] [,5]
[1,] 133.8735 133.8735 133.8735 133.8735 133.8735
[2,] 131.1321 131.3002 131.4766 131.6611 131.8534
[3,] 129.1470 129.5896 130.0545 130.5402 131.0453
[4,] 127.5945 128.3396 129.1167 129.9222 130.7523
[5,] 126.2633 127.2943 128.3593 129.4516 130.5652rownames(rmse)<-alpha
colnames(rmse)<-betap <- plot_ly(z = rmse,x=alpha,y=beta, type = "surface")
p %>% layout(scene = list(xaxis = list(title = 'alpha'),
yaxis = list(title = 'beta'),
zaxis = list(title = 'rmse')))par.min<-which(rmse==min(rmse),arr.ind=TRUE)
(alpha.min<-alpha[par.min[1]])[1] 0.27(beta.min<-beta[par.min[2]])[1] 0.69holt1<-holt(y,alpha=alpha.min,beta=beta.min , initial="simple")
holt1$modelHolt's method
Call:
holt(y = y, initial = "simple", alpha = alpha.min, beta = beta.min)
Smoothing parameters:
alpha = 0.27
beta = 0.69
Initial states:
l = 27
b = 28
sigma: 78.568accuracy(holt1) ME RMSE MAE MPE MAPE MASE ACF1
Training set 7.604673 78.56802 63.09934 -19.06109 37.73638 0.8388391 0.04764716holt2<-holt(y , initial="simple")
holt2$modelHolt's method
Call:
holt(y = y, initial = "simple")
Smoothing parameters:
alpha = 0.6179
beta = 0
Initial states:
l = 27
b = 28
sigma: 84.1316accuracy(holt2) #minimo local ME RMSE MAE MPE MAPE MASE
Training set 11.18843 84.13162 68.25252 -23.42833 40.63583 0.9073452
ACF1
Training set -0.01075344holt3<-holt(y , initial="optimal")
holt3$modelHolt's method
Call:
holt(y = y, initial = "optimal")
Smoothing parameters:
alpha = 0.2151
beta = 0.2149
Initial states:
l = -12.771
b = 40.3513
sigma: 83.865
AIC AICc BIC
347.0211 349.7484 353.6822 accuracy(holt3) ME RMSE MAE MPE MAPE MASE ACF1
Training set 3.588846 77.64386 58.89307 -19.83468 35.3691 0.7829212 0.052352773.3 Comparación Holt - Holt amortiguado
fc <- holt(y, h=15)
fc2 <- holt(y, damped=TRUE, h=15)
fc2$modelDamped Holt's method
Call:
holt(y = y, h = 15, damped = TRUE)
Smoothing parameters:
alpha = 0.2235
beta = 0.2235
phi = 0.9633
Initial states:
l = 23.4845
b = 21.8493
sigma: 86.4831
AIC AICc BIC
349.5510 353.5510 357.5442 ggplot2::autoplot(y) +
autolayer(fc, series="Holt", PI=FALSE) +
autolayer(fc2, series="Holt amortiguado", PI=FALSE) +
ggtitle('Pronóstico usando método Holt-Holt amortiguado') + xlab("Año") +
ylab("Graduados del ITCR (1975-2002)") +
guides(colour=guide_legend(title="Pronóstico"))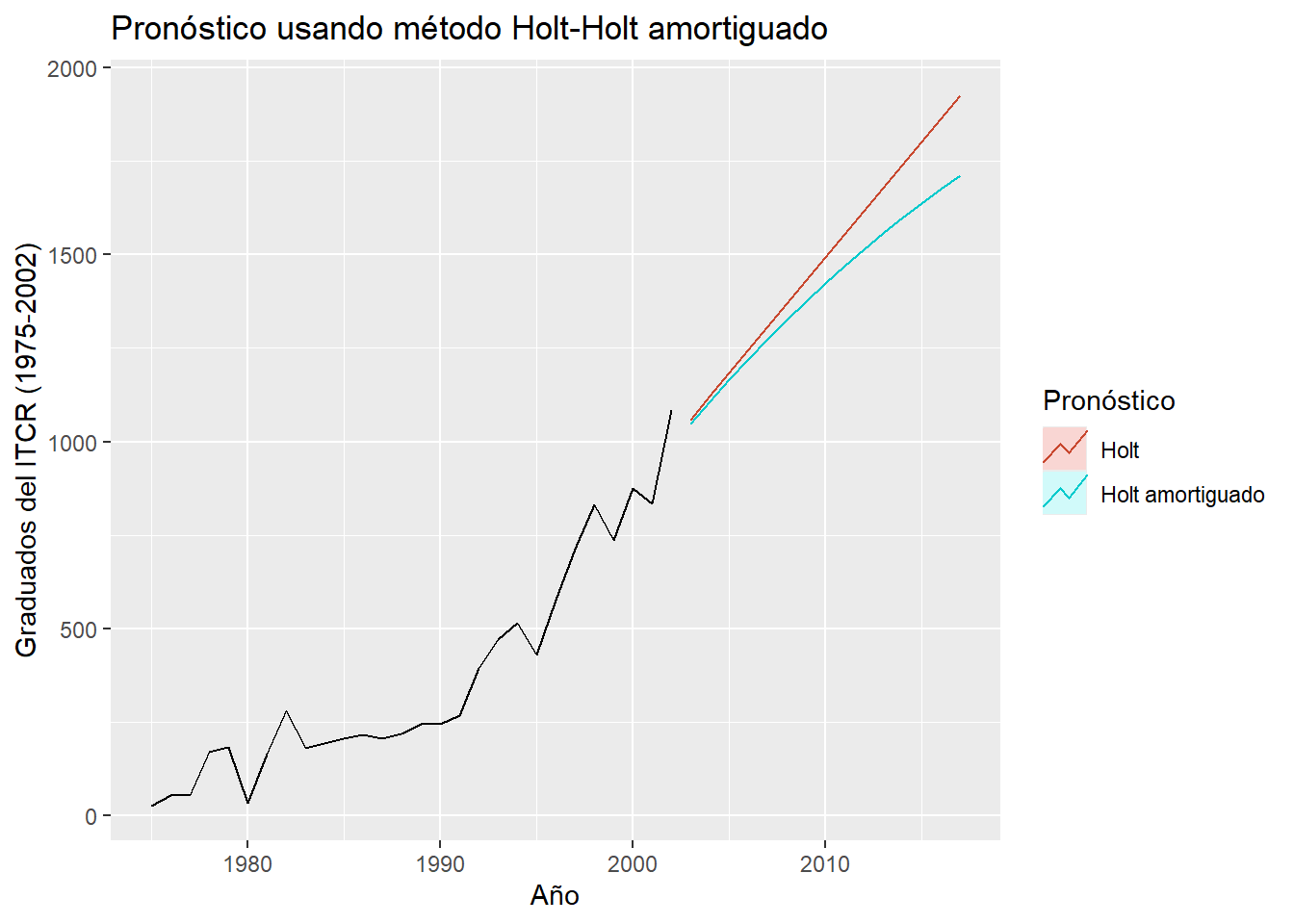
4 Método multiplicativo de Holt-Winters
turistas<-read.csv("turistas.csv",sep=";")
y<-ts(turistas$turistas,start=c(1991,1),frequency=12)
ts.plot(y)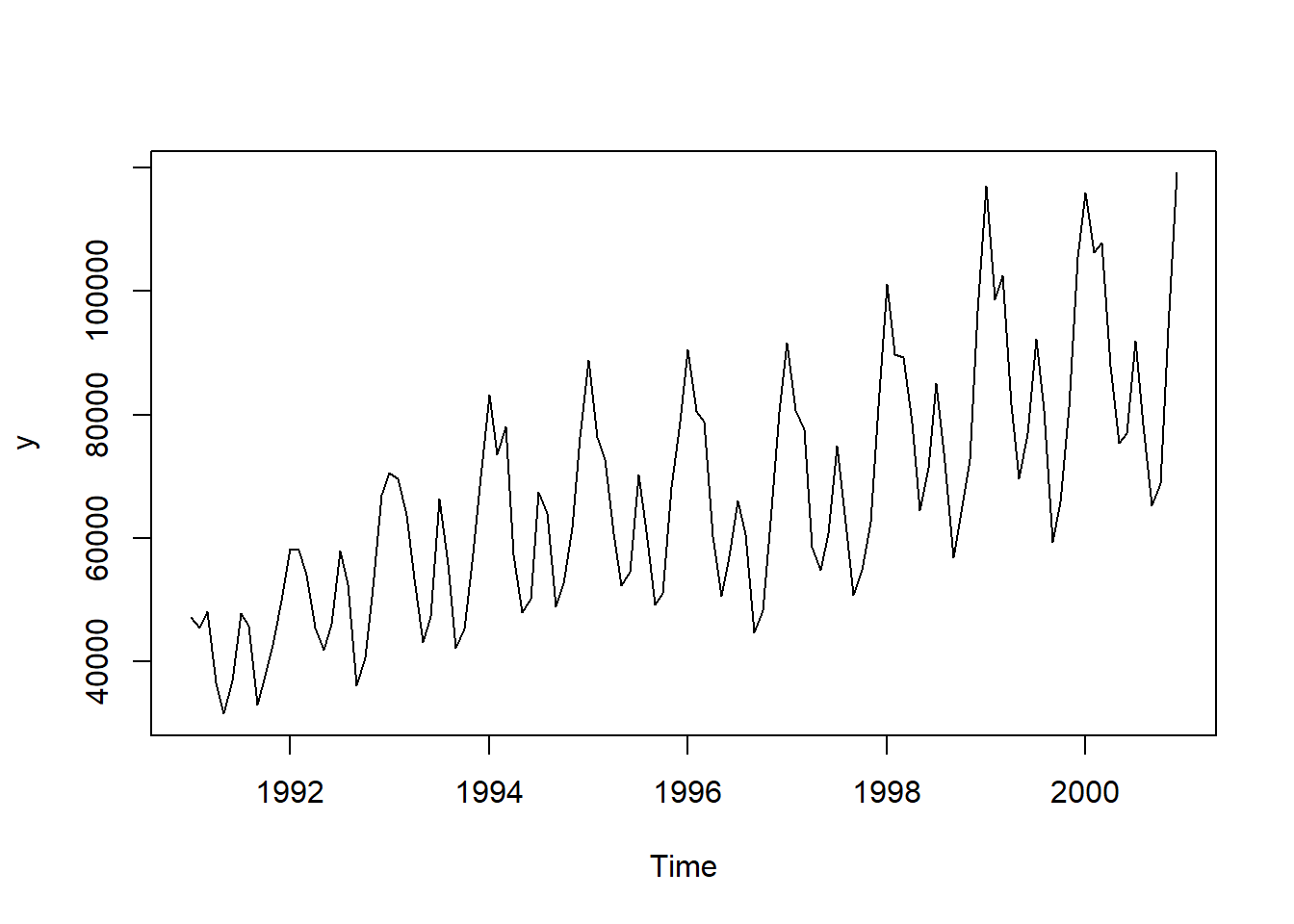
ht1 <- hw(y,seasonal="multiplicative")
names(ht1) [1] "model" "mean" "level" "x" "upper" "lower"
[7] "fitted" "method" "series" "residuals"ht1$modelHolt-Winters' multiplicative method
Call:
hw(y = y, seasonal = "multiplicative")
Smoothing parameters:
alpha = 0.645
beta = 0.0152
gamma = 1e-04
Initial states:
l = 40683.2372
b = 789.1426
s = 1.185 0.9434 0.7671 0.7137 0.935 1.0741
0.8724 0.8106 0.9515 1.1889 1.2062 1.3522
sigma: 0.053
AIC AICc BIC
2542.932 2548.932 2590.319 ht2 <- hw(y,seasonal="additive")
ht3 <- hw(y, damped=TRUE, seasonal="multiplicative")
ht3$modelDamped Holt-Winters' multiplicative method
Call:
hw(y = y, seasonal = "multiplicative", damped = TRUE)
Smoothing parameters:
alpha = 0.66
beta = 0.024
gamma = 1e-04
phi = 0.9684
Initial states:
l = 37734.1221
b = 789.7191
s = 1.1839 0.9441 0.7666 0.7176 0.939 1.0778
0.8739 0.8108 0.9503 1.1853 1.2078 1.3431
sigma: 0.0525
AIC AICc BIC
2539.896 2546.668 2590.071 autoplot(y) +
autolayer(ht1, series="HW multiplicativo", PI=FALSE, size = 1.2) +
autolayer(ht2, series="HW aditivo", PI=FALSE, size = 1.2) +
autolayer(ht3, series="HW M. amortiguado", PI=FALSE, size = 1.2) +
xlab("fecha") +
ylab("turistas") +
ggtitle("Turistas que ingresaron a CR") +
guides(colour=guide_legend(title="pronóstico"))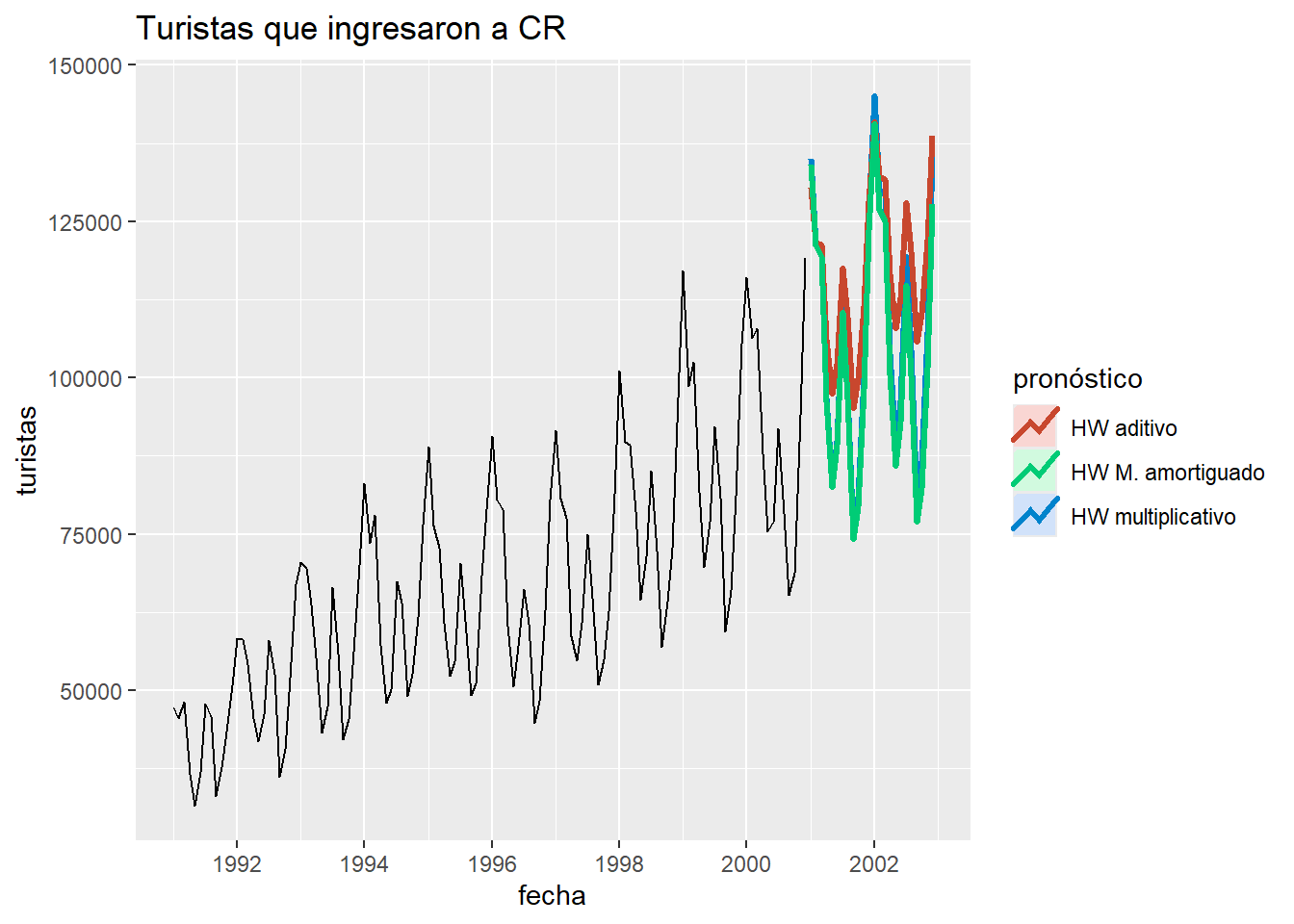
accuracy(ht1) ME RMSE MAE MPE MAPE MASE
Training set -114.3084 3239.923 2580.033 -0.3986991 3.995136 0.4245259
ACF1
Training set 0.008128625accuracy(ht2) ME RMSE MAE MPE MAPE MASE
Training set -394.643 4297.824 3312.546 -0.7003905 5.216058 0.5450557
ACF1
Training set -0.003603756accuracy(ht3) ME RMSE MAE MPE MAPE MASE
Training set 309.2038 3213.097 2587.598 0.2712205 3.958626 0.4257708
ACF1
Training set -0.019307395 ETS como modelo Espacio de Estados
hw_ad<-ets(y,model="AAA",damped = FALSE)
hw_ad_a<-ets(y,model="AAA",damped = TRUE)
hw_mul<-ets(y,model="MAM",damped = FALSE)
hw_mul_a<-ets(y,model="MAM",damped = TRUE)
hw_auto<-ets(y,model="ZZZ") #selecciona el mejor modelo usando AIC.
accuracy(hw_ad) ME RMSE MAE MPE MAPE MASE
Training set -394.6563 4297.824 3312.536 -0.7004108 5.216048 0.5450541
ACF1
Training set -0.003568228accuracy(hw_ad_a) ME RMSE MAE MPE MAPE MASE ACF1
Training set 260.7423 4254.83 3302.818 0.2544367 5.10127 0.543455 0.00139745accuracy(hw_mul) ME RMSE MAE MPE MAPE MASE
Training set -296.167 3301.525 2602.353 -0.7057268 3.976193 0.4281986
ACF1
Training set 0.07227753accuracy(hw_mul_a) ME RMSE MAE MPE MAPE MASE ACF1
Training set 372.8259 3283.797 2633.531 0.3366449 3.939674 0.4333287 0.07885943accuracy(hw_auto) ME RMSE MAE MPE MAPE MASE ACF1
Training set 372.8259 3283.797 2633.531 0.3366449 3.939674 0.4333287 0.07885943hw_auto <- ets(y)
summary(hw_auto)ETS(M,Ad,M)
Call:
ets(y = y)
Smoothing parameters:
alpha = 0.5798
beta = 1e-04
gamma = 1e-04
phi = 0.9774
Initial states:
l = 37996.857
b = 809.5089
s = 1.1769 0.9461 0.7722 0.7183 0.955 1.0858
0.8657 0.8016 0.9472 1.1851 1.2074 1.3387
sigma: 0.0516
AIC AICc BIC
2535.688 2542.460 2585.863
Training set error measures:
ME RMSE MAE MPE MAPE MASE ACF1
Training set 372.8259 3283.797 2633.531 0.3366449 3.939674 0.4333287 0.07885943autoplot(hw_auto)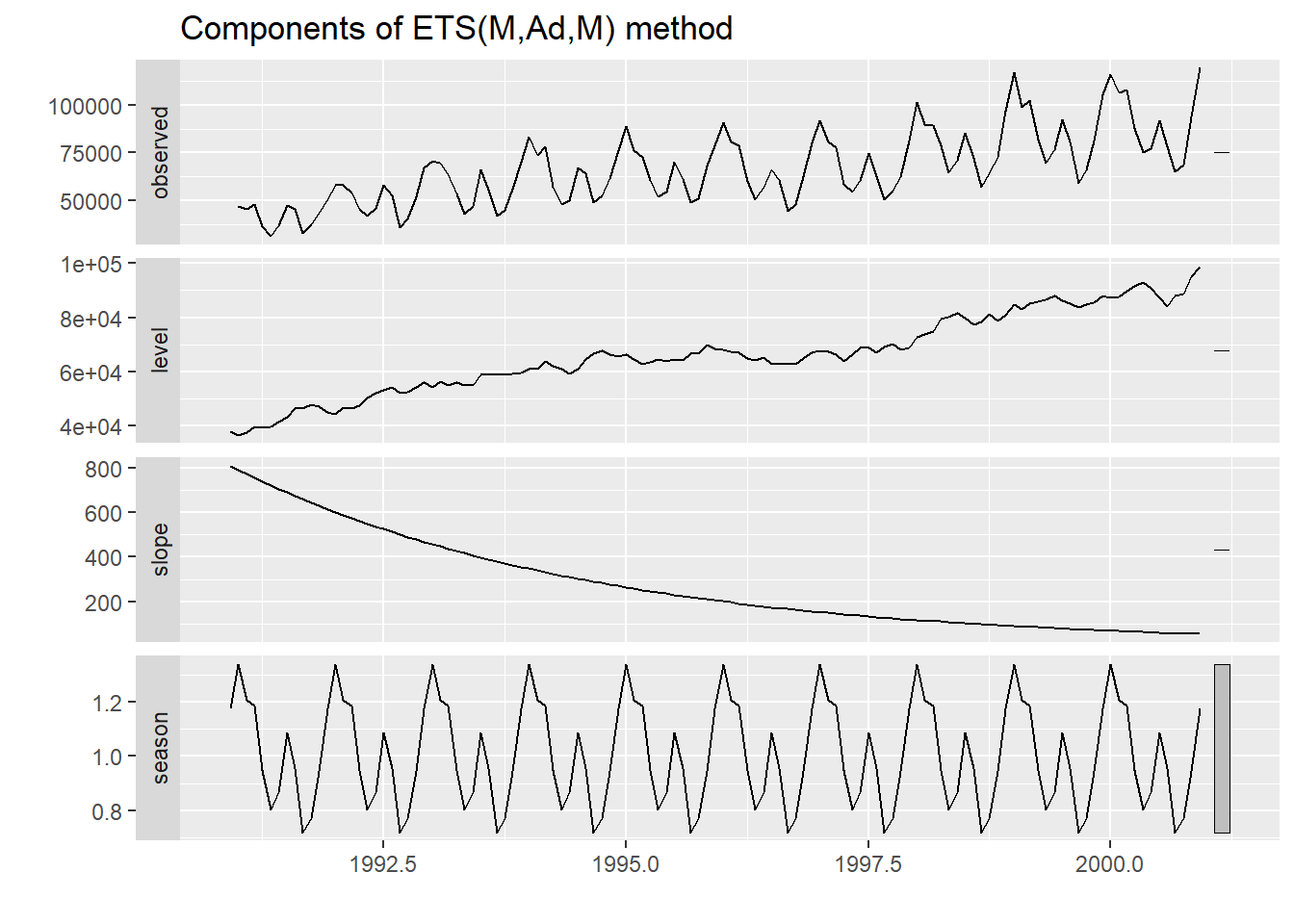
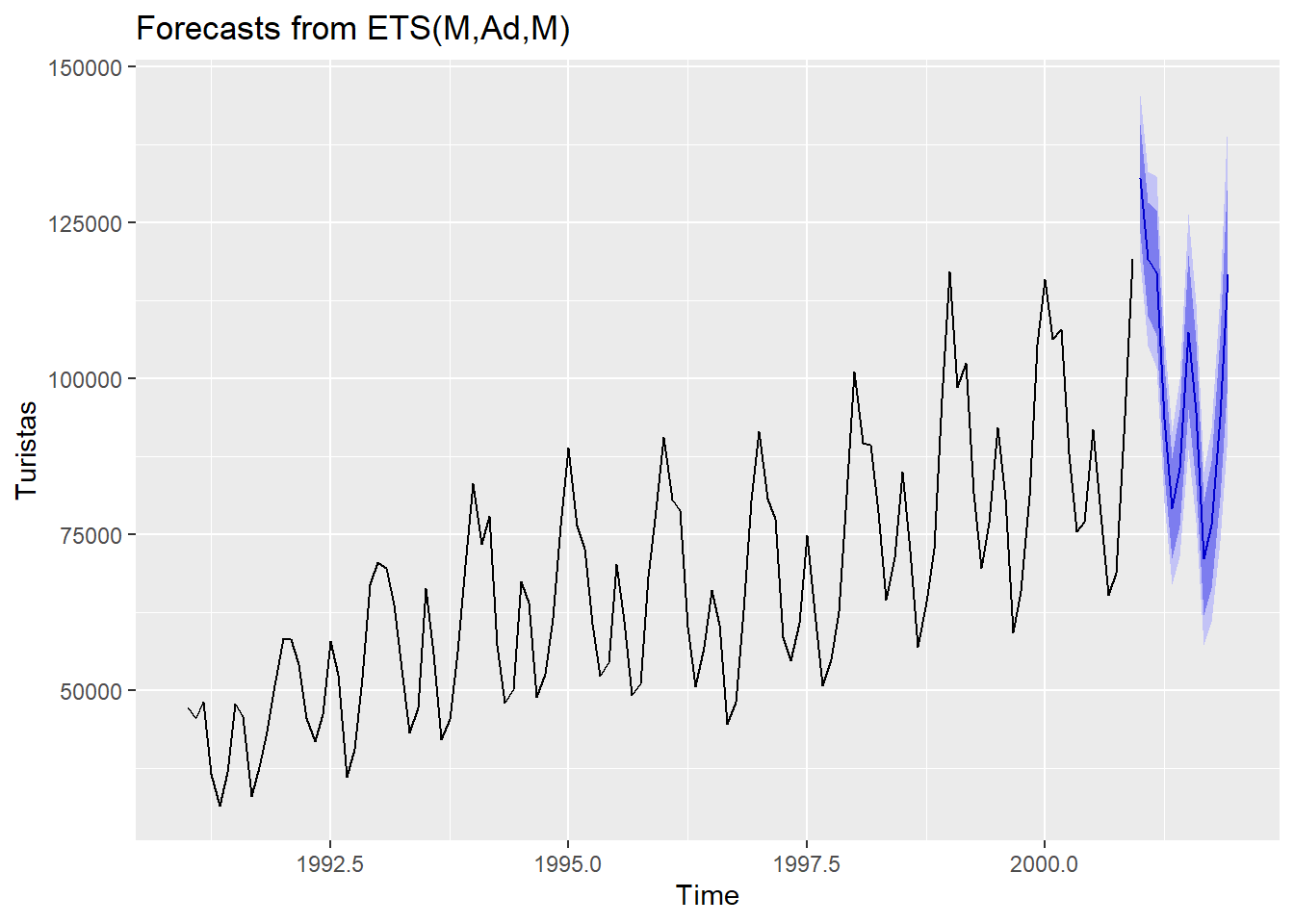
plot(forecast(hw_auto))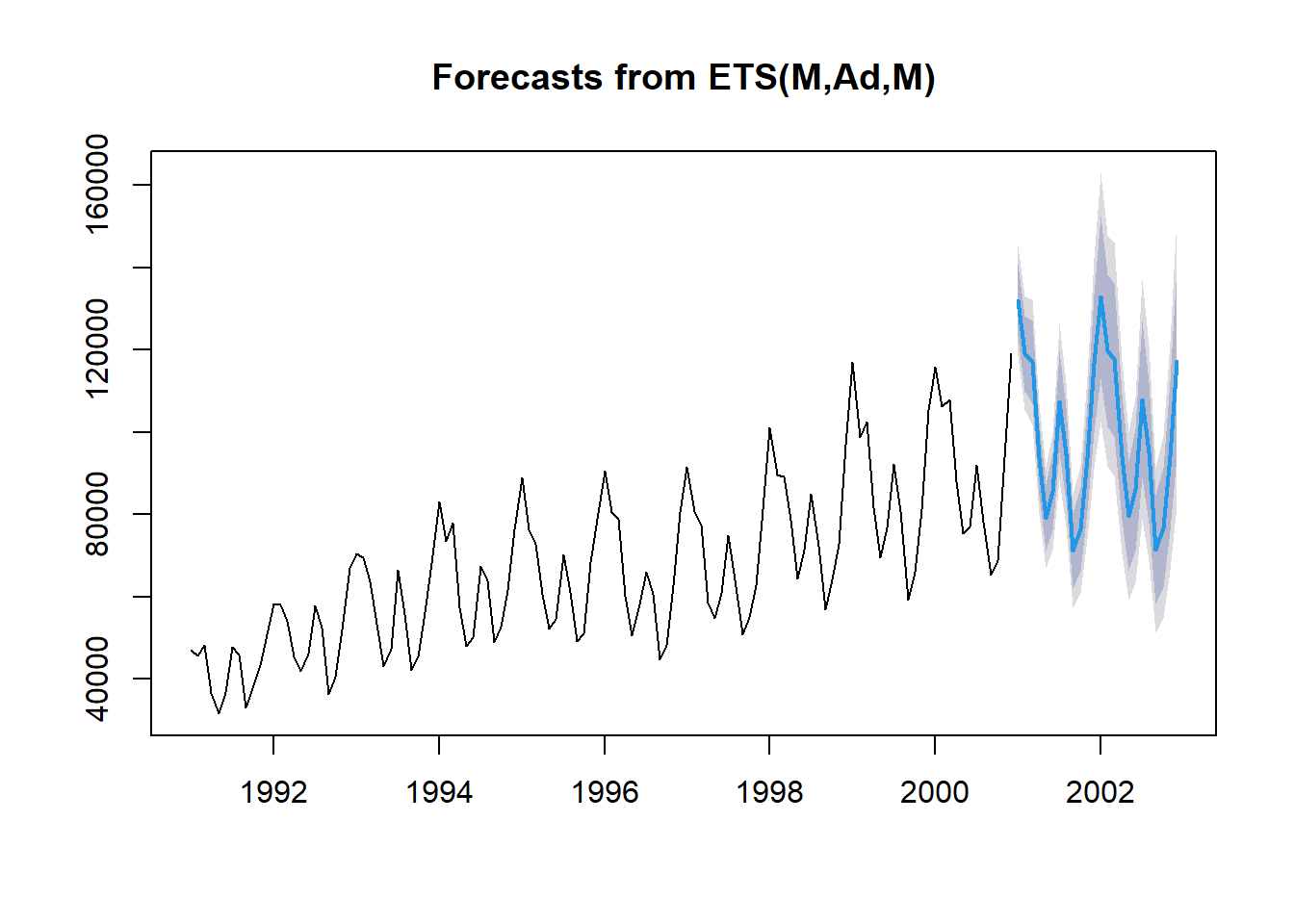
hw_auto %>% forecast(h=12) %>%
autoplot() +
ylab("Turistas")