Tema 1: Análisis espectral de series temporales⁽⁴⁾

Curso: Tópicos Avanzados de Series Temporales

Shu Wei Chou Chen

shuwei.chou@ucr.ac.cr

Escuela de Estadística, Universidad de Costa Rica

Estimación espectral no paramétrica

Contenido

Estimación espectral no paramétrica
Estimación espectral no paramétrica (extensión)
Estimación espectral paramétrica

Estimación espectral no paramétrica

Para introducir la estimación espectral no paramétrica, es necesario definir el concepto de una banda en el dominio de frecuencia \(\mathcal{B}\), de \(L \ll T\) contiguas frecuencias fundamentales, que estén centrado alrededor de la frecuencia de interés \(\omega_j=\frac{j}{T}\) (cercano a \(\omega\) de interés).
Para frecuencias de la forma \(\omega^*=w_j+\frac{k}{T}\), sea

\[\mathcal{B} = \left\lbrace \omega^*: \omega_j-\frac{m}{T} \leq \omega^* \leq \omega_j+\frac{m}{T}\right\rbrace,\] donde \(L=2m+1\) (número impar), selecionado de tal forma que el valor espectral en el intervalo \(\mathcal{B}\) \[f\left(\omega_j+\frac{k}{T}\right),~~k=-m,...,0,...,m.\] sea similar a \(f(\omega)\).

Podemos definir el periodograma suavizado (promediado) como:

\[\bar{f}(\omega)=\frac{1}{L}\sum_{k=-m}^{m}I\left(\omega_j+\frac{k}{T}\right).\]

Bajo ciertas condiciones de regularidad, se puede obtener resultados asintóticos similares a propiedades de la distribución del periodograma (no suavizado), i.e. cuando \(T \rightarrow \infty\),

\[\frac{2 L~ \bar{f}(\omega)}{f(\omega)} \rightarrow \chi^2_{2L}.\]

Note que las bandas de frecuencias \(\mathcal{B}\) tienen tamaño \(B=\frac{L}{T}\).
Finalmente, se puede construir un intervalo de confianza de \(100(1-\alpha)\%\), con \[\frac{2L \bar{f}(\omega)}{\chi^2_{2L}(1-\alpha/2)}<f(\omega)<\frac{2L \bar{f}(\omega)}{\chi^2_{2L}(\alpha/2)}.\]

Debido a la asimetría de la distribución del periodograma, se puede utilizar el logarítmo del espectro para facilitar la visualización.
Es decir, se puede construir un intervalo de confianza de \(100(1-\alpha)\%\) con escala logarítmica, usando \[\left[ \log \bar{f}(\omega)+a_L~,~\log \bar{f}(\omega) + b_L \right]\] donde
\(a_L = \log 2L - \log \chi^2_{2L} (1-\alpha/2)\) y
\(b_L = \log 2L - \log \chi^2_{2L} (\alpha/2)\).

Si \(L\) es muy cercano a cero, puede producir problema en la computación. Se utiliza una aproximación reemplazando \(2L\) por \(2Ln/n'\). De esta forma, se define los grados de libertad ajustados como \[df=\frac{2Ln}{n'}\]
Finalmente, el intervalo de confianza de \(100(1-\alpha)\%\) queda: \[\frac{df~ \bar{f}(\omega)}{\chi^2_{df}(1-\alpha/2)}<f(\omega)<\frac{df~ \bar{f}(\omega)}{\chi^2_{df}(\alpha/2)}.\]

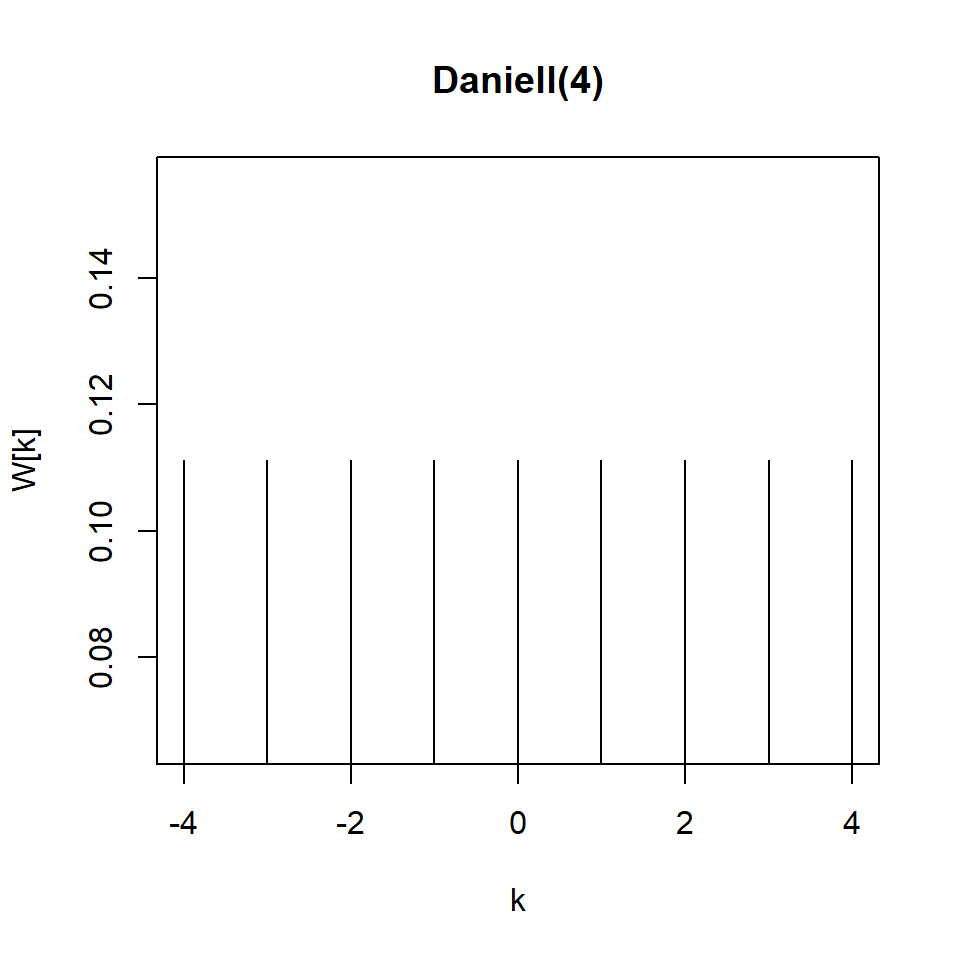
Núcleo de Danniell

Más adelante, veremos que “promediando” las frecuencias de una banda se trata del uso del núcleo de Danniell.
Utilizando \(m=4\) y \(L=2m+1=9\) como ejemplo:

kernel('daniell',4)

Daniell(4) 
coef[-4] = 0.1111
coef[-3] = 0.1111
coef[-2] = 0.1111
coef[-1] = 0.1111
coef[ 0] = 0.1111
coef[ 1] = 0.1111
coef[ 2] = 0.1111
coef[ 3] = 0.1111
coef[ 4] = 0.1111

plot(kernel("daniell", 4))

Ejemplo: SOI y reclutamiento

Espectro

par(mfrow=c(2,1))
soi.ave = mvspec(soi, kernel('daniell',4))

Bandwidth: 0.225 | Degrees of Freedom: 16.99 | split taper: 0%

abline(v = c(.25,1,2,3), lty=2)

soi.rec = mvspec(rec, kernel('daniell',4))

Bandwidth: 0.225 | Degrees of Freedom: 16.99 | split taper: 0%

abline(v=c(.25,1,2,3), lty=2)

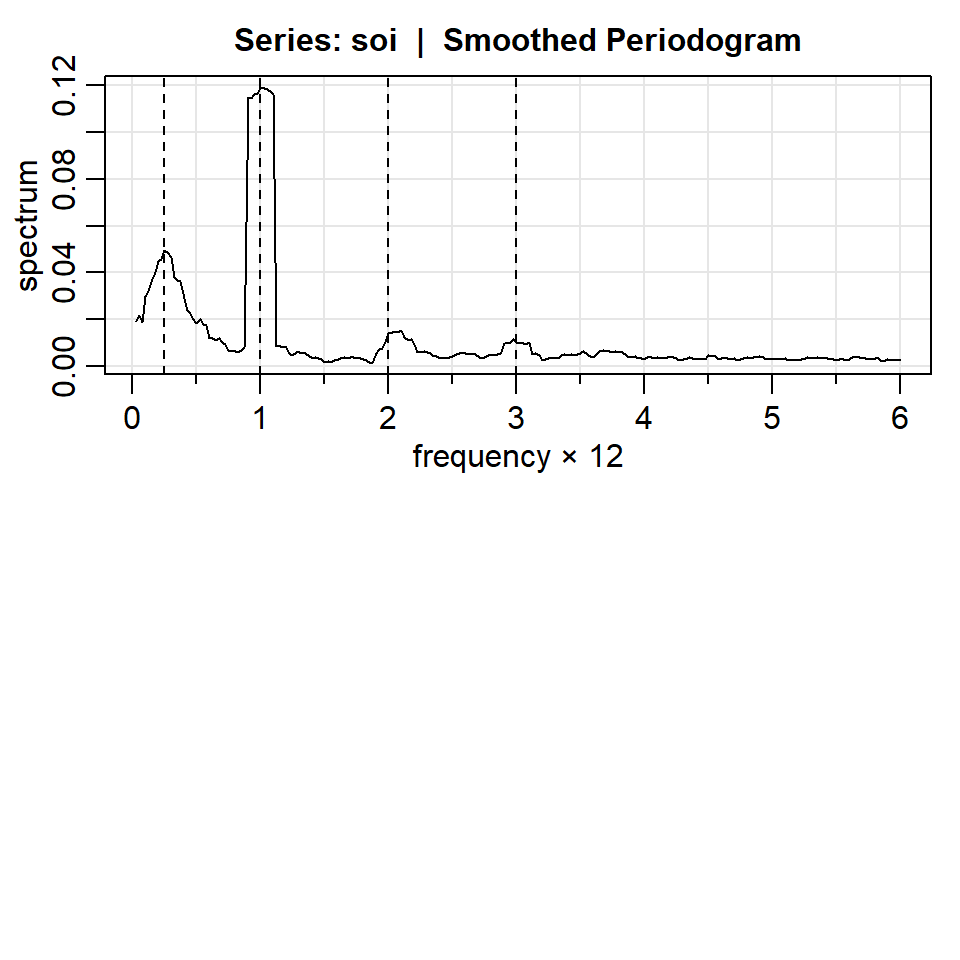
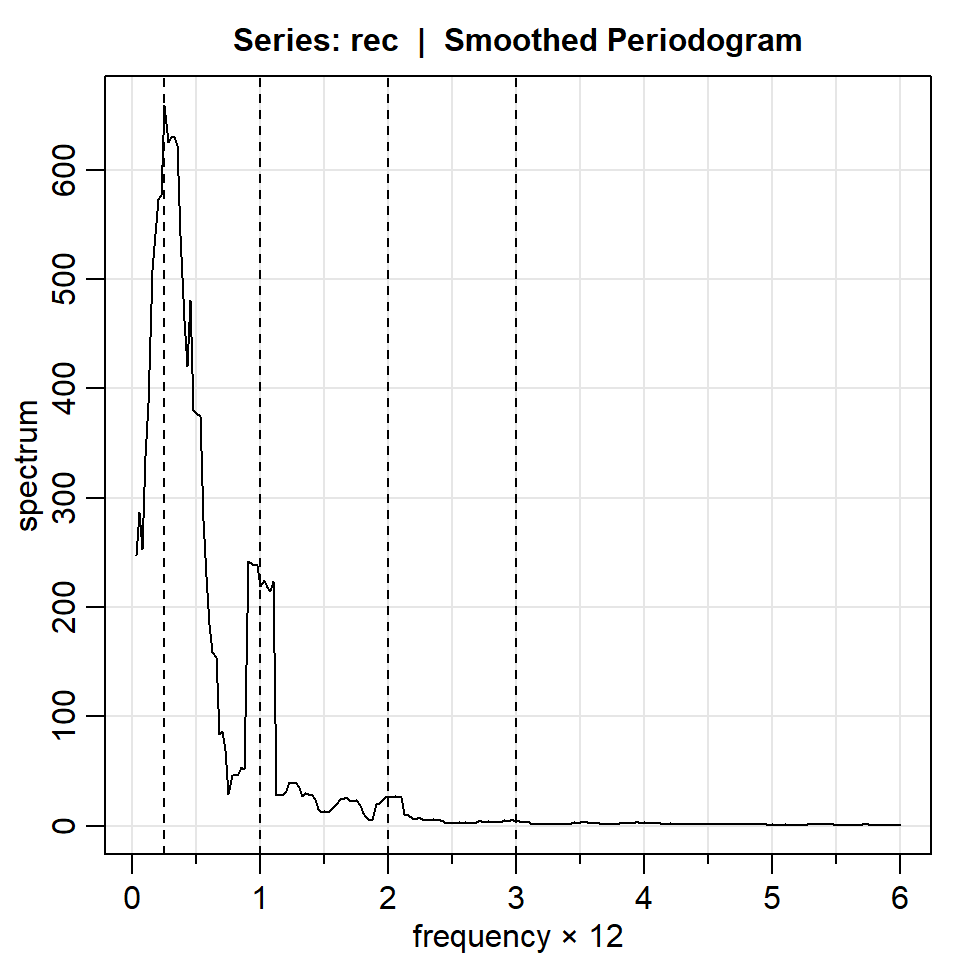
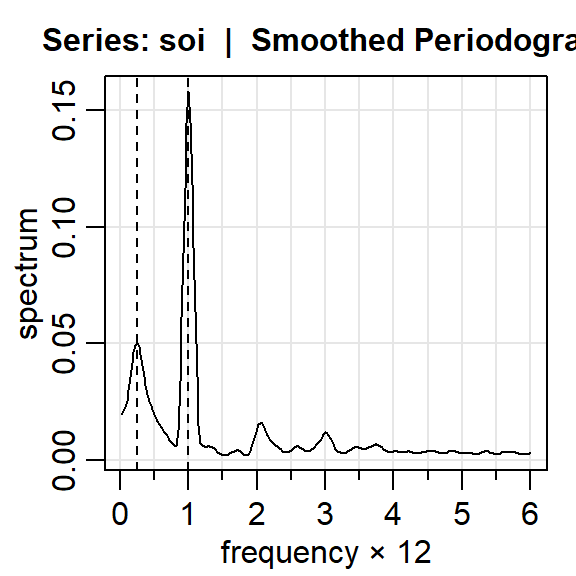
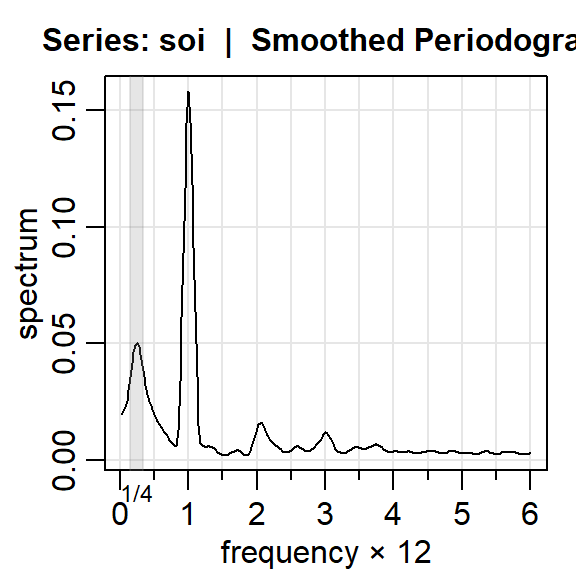
Al igual que el periodograma no suavizado, los picos principales son de las frecuencias:
- \(\omega=1/4\Delta=1/48\) ciclos por mes (4 años), y
- \(\omega=1\Delta=1/12\) ciclos por mes (anual).
Note que hay picos sucesivos en las frecuencias \(k\omega\), \(k=2,3\). Esto es debido a la presencia de componentes periódicos no sinusoidal.
Ejercicio: Interprete el espectro de REC.

El intervalo de confianza se obtiene a continuación:

df  = soi.ave$df     
U   = qchisq(.025, df) 
L   = qchisq(.975, df) 
soi.ave$spec[10]

[1] 0.04952026

soi.ave$spec[40]

[1] 0.11908

# para frecuencia= 1/4
round(c(df*soi.ave$spec[10]/L,df*soi.ave$spec[10]/U),4)

[1] 0.0279 0.1113

# para frecuencia= 1
round(c(df*soi.ave$spec[40]/L,df*soi.ave$spec[40]/U),4)

[1] 0.0670 0.2677

Espectro logarítmico

par(mfrow=c(2,1))
soi.ave = mvspec(soi, kernel('daniell',4),log="yes")

Bandwidth: 0.225 | Degrees of Freedom: 16.99 | split taper: 0%

abline(v = c(.25,1,2,3), lty=2)
soi.ave = mvspec(rec, kernel('daniell',4),log="yes")

Bandwidth: 0.225 | Degrees of Freedom: 16.99 | split taper: 0%

abline(v=c(.25,1,2,3), lty=2)

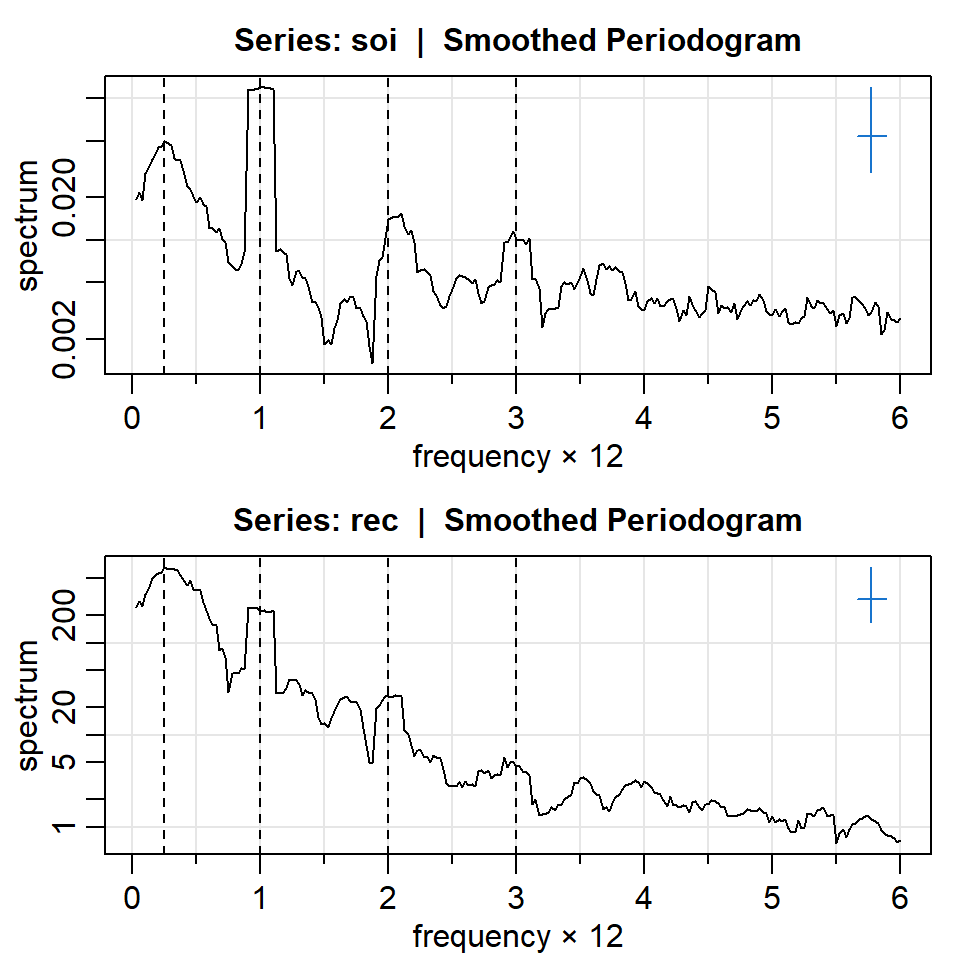
Nota

El ancho de la cruz representa el ancho de la banda y el largo representa el intervalo de confianza.
Se notan picos del periodograma en los múltiplos de \(\Delta\). Esto es debido a que el comportamiento cíclico no es sinusoidal perfecto.

Ejemplo: Armónicos

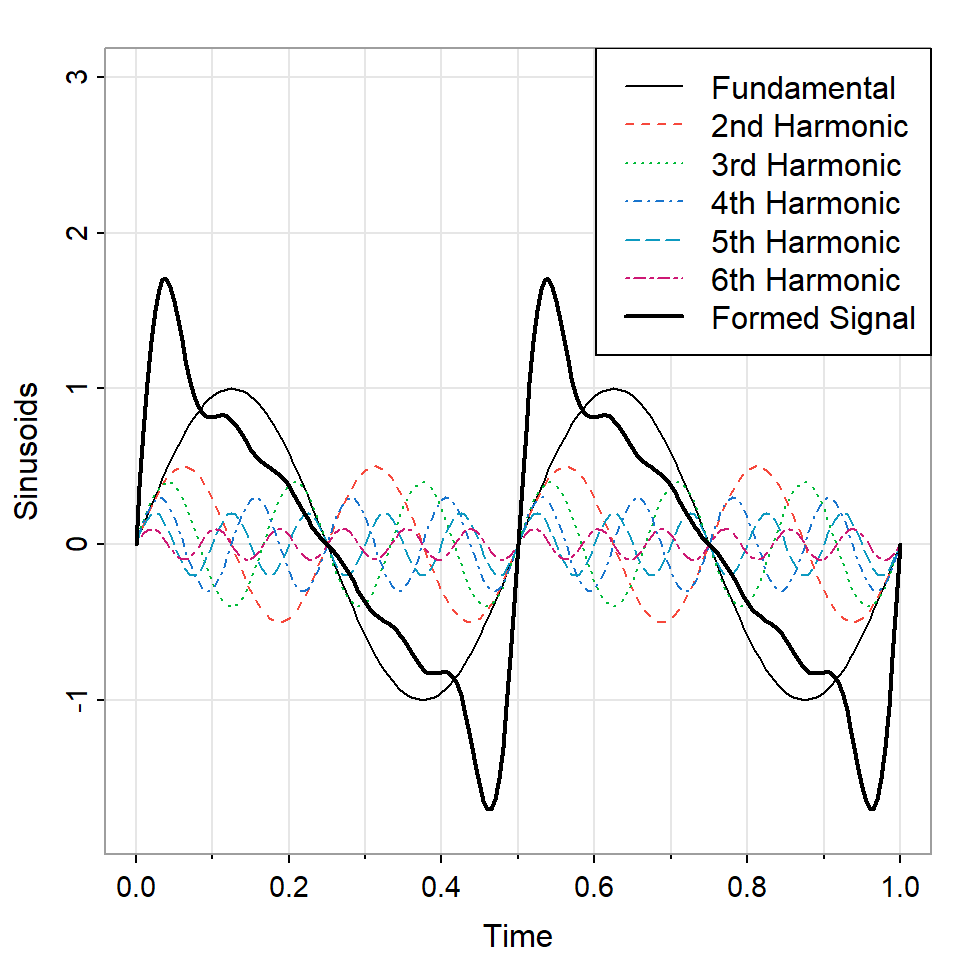
Para ilustrar un comportamiento ciclico que no es sinusoidal, pero se puede formarlo con armónicas fundamentales.
Considere \[x_t=\sin(2\pi2t)+0.5\sin(2\pi4t)\] \[+0.4\sin(2\pi6t)+0.3\sin(2\pi10t)\] \[+0.1\sin(2\pi12t)\]
Esta función es periódica, pero no es sinusoidal.

Estimación espectral no paramétrica (extensión)

Contenido

Estimación espectral no paramétrica
Estimación espectral no paramétrica (extensión)
Estimación espectral paramétrica

Estimación espectral no paramétrica (extensión)

Se puede extender el periodograma suavizado (promediado) con:

\[\hat{f}(\omega)=\sum_{k=-m}^{m} h_k I(\omega_j+k/T)\] donde los pesos \(h_k>0\) y cumple la condición \[\sum_{k=-m}^{m} h_k>0.\]

Es posible obtener resultados asintóticos pero no vamos a entrar en detalles.

Alternativas de núcleos

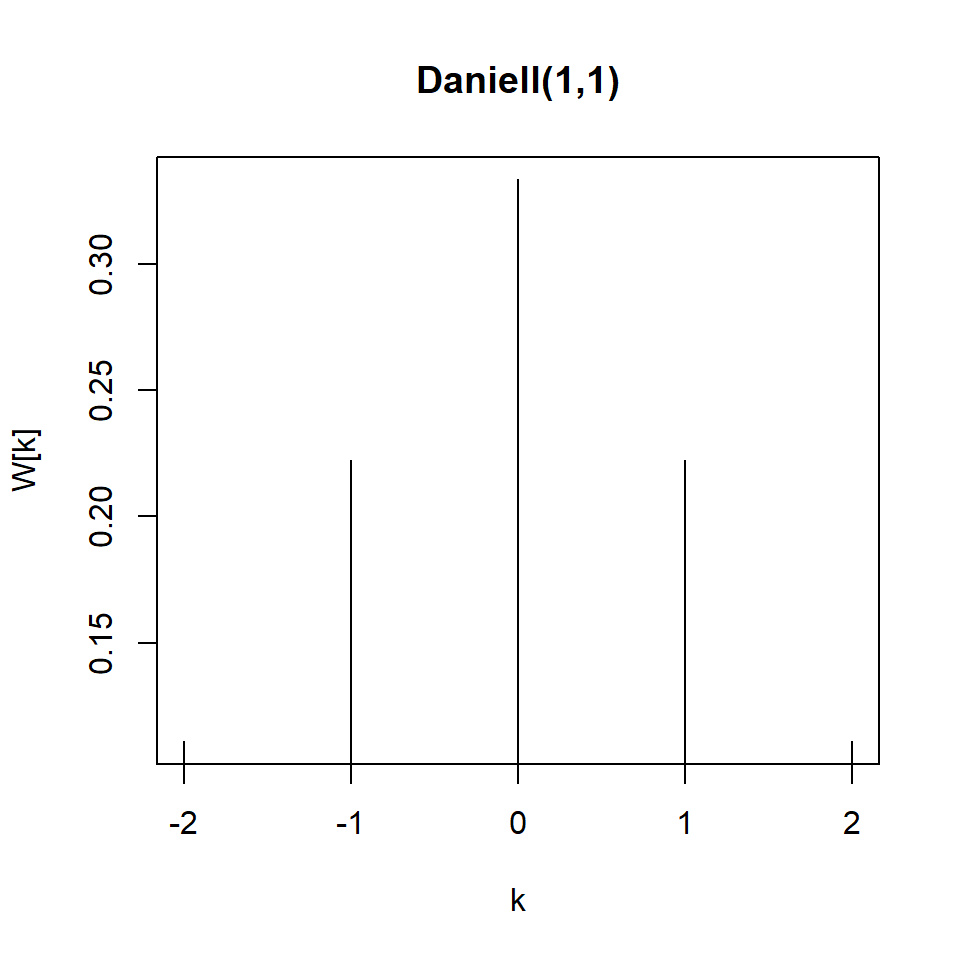
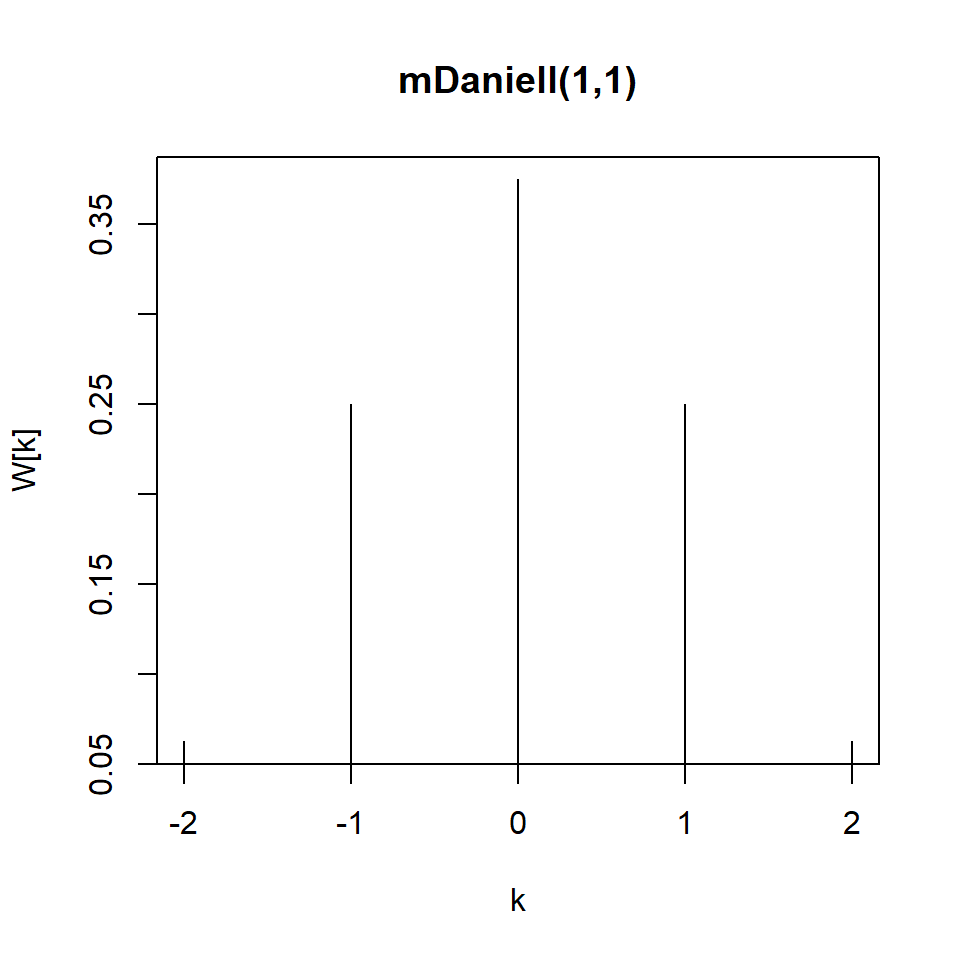
Una forma de crear pesos diferentes es repetir varias veces el núcleo de Daniell.
Considere una secuencia de valores \(u_t\), el núcleo de Daniell con \(m=1\) es: \[\hat{u}_{t}=\frac{1}{3}u_{t-1}+\frac{1}{3}u_{t}+\frac{1}{3}u_{t+1}\]
Aplicamos nuevamente el núcleo de Daniell con \(k=1\):

\[\hat{\hat{u}}_{t}=\frac{1}{3}\hat{u}_{t-1}+\frac{1}{3}\hat{u}_{t}+\frac{1}{3}\hat{u}_{t+1}\]

Se obtiene

\[\hat{\hat{u}}_{t}=\frac{1}{9}u_{t-2}+\frac{2}{9}u_{t-1}+\frac{3}{9}u_{t}+\frac{2}{9}u_{t+1}+\frac{1}{9}u_{t+2}\]

kernel("daniell", c(1))

Daniell(1) 
coef[-1] = 0.3333
coef[ 0] = 0.3333
coef[ 1] = 0.3333

kernel("daniell", c(1,1))

Daniell(1,1) 
coef[-2] = 0.1111
coef[-1] = 0.2222
coef[ 0] = 0.3333
coef[ 1] = 0.2222
coef[ 2] = 0.1111

plot(kernel("daniell", c(1,1)))

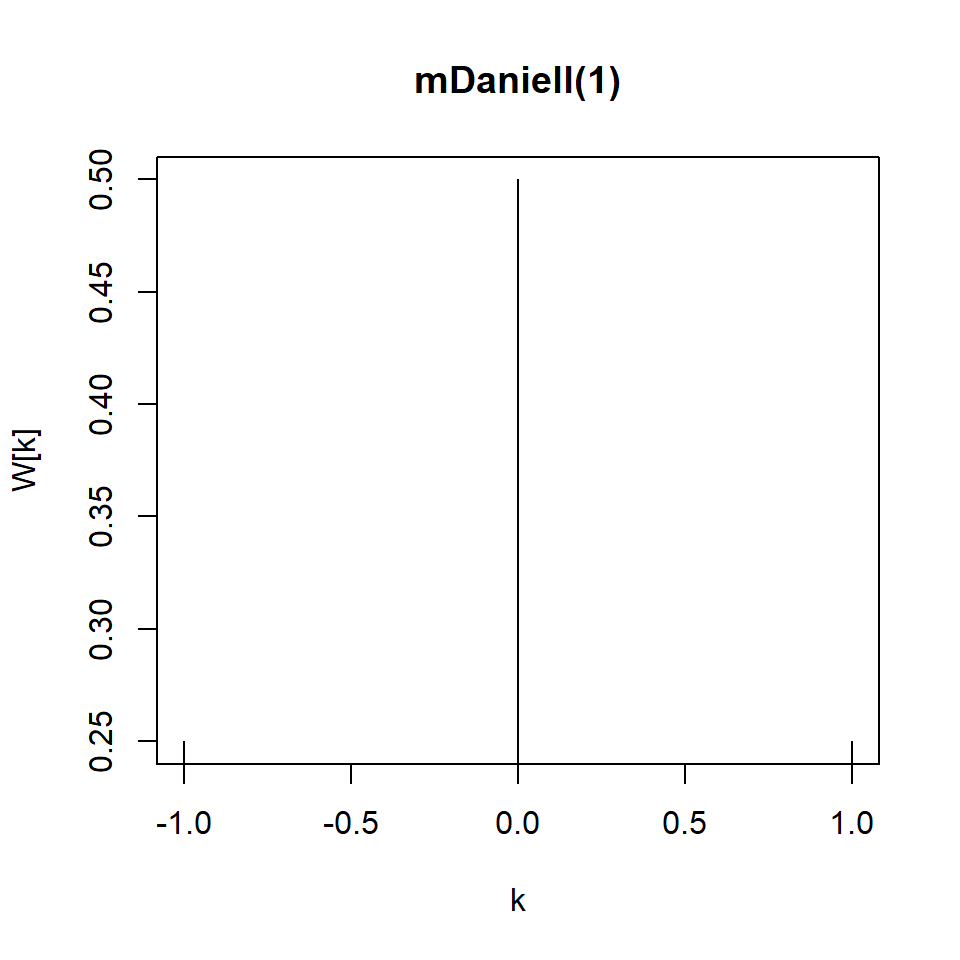
El núcleo (kernel) de Daniell modificado asigna mitad del peso en los extremos.

kernel("modified.daniell", c(1))

mDaniell(1) 
coef[-1] = 0.25
coef[ 0] = 0.50
coef[ 1] = 0.25

plot(kernel("modified.daniell", c(1)))

Considere una secuencia de valores \(u_t\), el núcleo de Daniell modificado con \(m=1\) es: \[\hat{u}_{t}=\frac{1}{4}u_{t-1}+\frac{1}{2}u_{t}+\frac{1}{4}u_{t+1}\]
Aplicamos nuevamente el núcleo de Daniell modificado con \(k=1\), se obtiene

\[\hat{\hat{u}}_{t}=\frac{1}{16}u_{t-2}+\frac{4}{16}u_{t-1}+\frac{6}{16}u_{t}+\frac{4}{16}u_{t+1}+\frac{1}{16}u_{t+2}\]

kernel("modified.daniell", c(1,1))

mDaniell(1,1) 
coef[-2] = 0.0625
coef[-1] = 0.2500
coef[ 0] = 0.3750
coef[ 1] = 0.2500
coef[ 2] = 0.0625

plot(kernel("modified.daniell", c(1,1)))

Ejemplo: SOI y reclutamiento

Aaplicando el núcleo (kernel) de Daniell modificado

k        = kernel("modified.daniell", c(3,3))
soi.smo  = mvspec(soi, kernel=k, taper=0)

Bandwidth: 0.231 | Degrees of Freedom: 17.43 | split taper: 0%

abline(v = c(.25,1), lty=2)

soi.smo$df           # df = 17.42618

[1] 17.42618

soi.smo$bandwidth    # B  = 0.2308103

[1] 0.2308103

# Otra forma de hacer es con el argumento `spans`
soi.smo1 = mvspec(soi, spans=c(7,7), taper=0)  #7=3*2+1

Bandwidth: 0.231 | Degrees of Freedom: 17.43 | split taper: 0%

# El ciclo del Niño
rect(1/7, -1e5, 1/3, 1e5, density=NA, col=gray(.5,.2))
mtext("1/4", side=1, line=0, at=.25, cex=.75)

Estimación espectral paramétrica

Contenido

Estimación espectral no paramétrica
Estimación espectral no paramétrica (extensión)
Estimación espectral paramétrica

Estimación espectral paramétrica

Consiste en construir la función espectral utilizando las estimaciones de un modelo ARIMA(p,q).
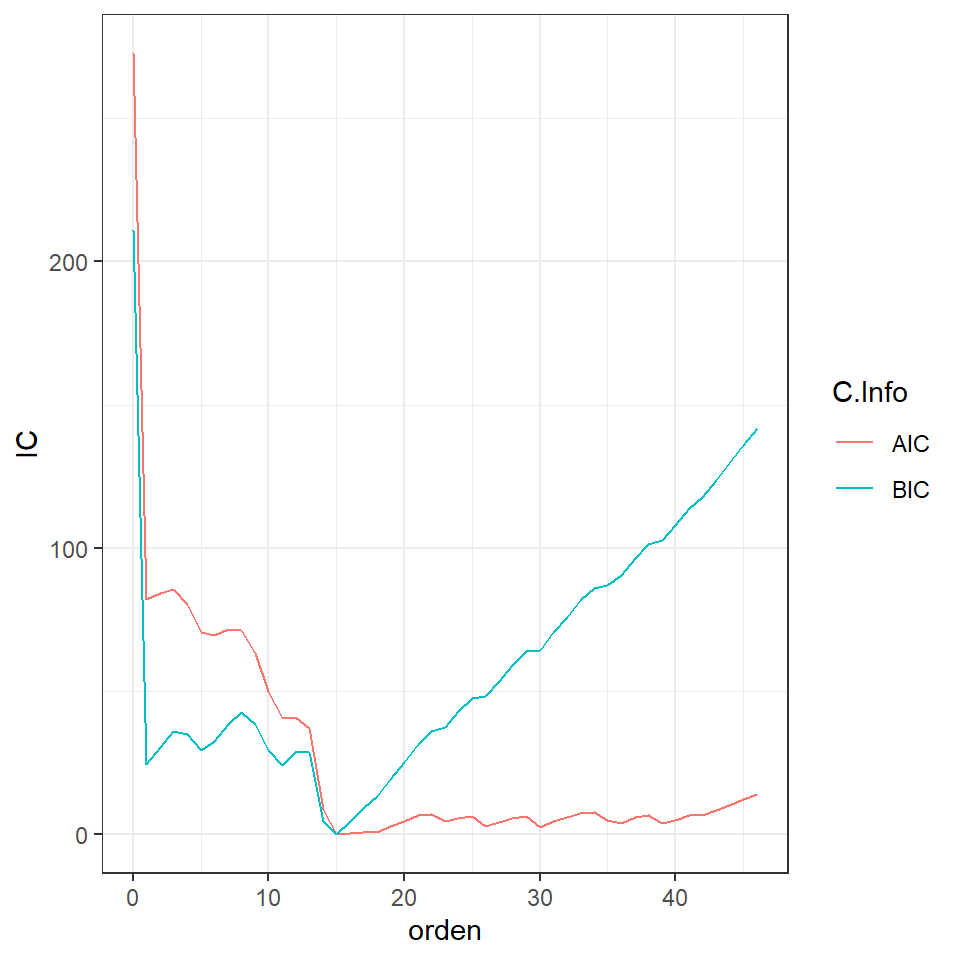
En la práctica, es común utilizar los criterios de información como AIC, AICc y BIC para seleccionar el mejor orden p de AR(p).
A partir de las estimaciones, se calcula la densidad espectral utilizando:

\[\hat{f}_X(\omega)= \frac{\hat{\sigma}_w^2}{|\hat{\phi}(e^{-2 \pi i \omega})|^2}.\] donde \(\hat{\phi}(B)=1-\hat{\phi}_1 B -\hat{\phi}_2 B^2-...-\hat{\phi}_p B^p\).

Bajo condiciones \(p \rightarrow \infty, p^3/T \rightarrow 0\) cuando \(p,T \rightarrow \infty\), el intervalo de confianza de \(100(1-\alpha)\%\) queda: \[\frac{\hat{f}(\omega)}{1+C z_{\alpha/2}}<f_X(\omega)<\frac{\hat{f}(\omega)}{1-Cz_{\alpha/2}},\] donde \(C=\sqrt{2p/T}\) y \(z_{\alpha/2}\) es el percentil \(1-\alpha/2\) de la distribución normal estándar.
¿Por qué con AR(p)? La densidad espectral de cualquier proceso estacionario puede ser aproximado por la densidad espectral de AR(p) (ver Propiedad 4.7 de Shumway & Stoffer).

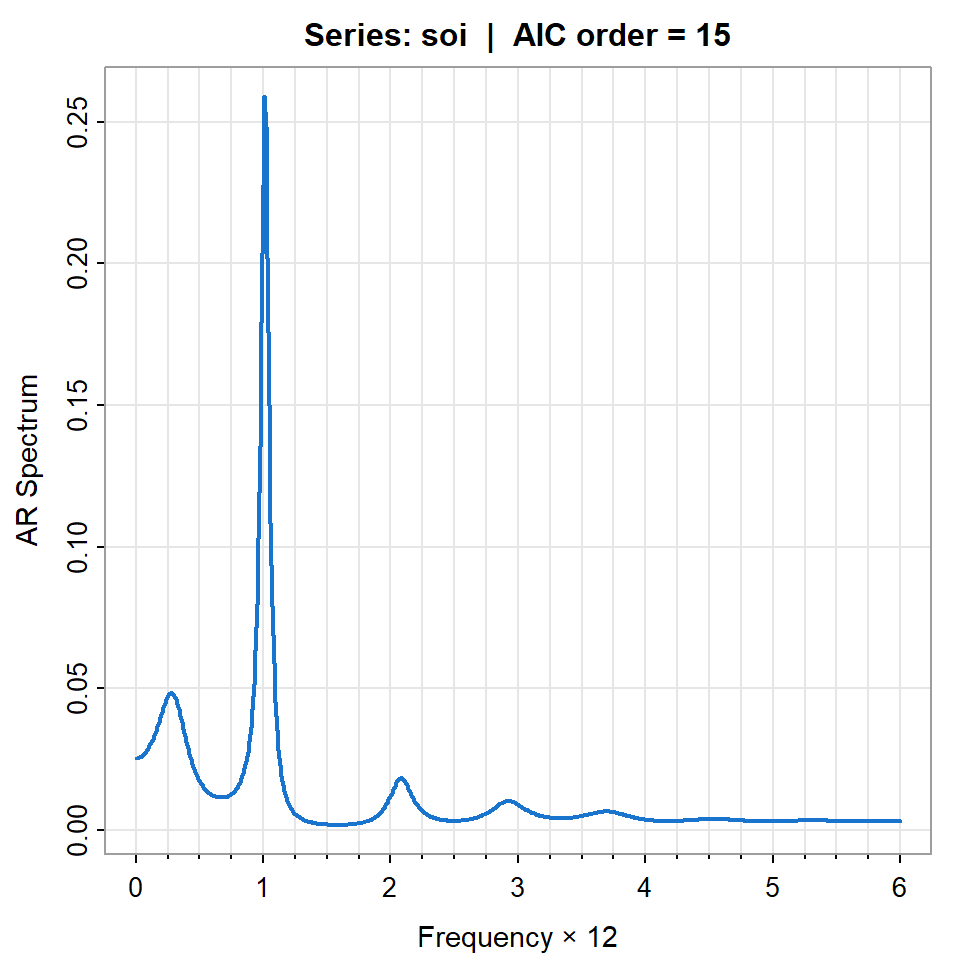
Ejemplo

En R, el comando spec.ic escoge el mejor rezago de acuerdo a AIC.

param.spec <- spec.ic(soi,  detrend=TRUE, col=4, lwd=2, nxm=4)

head(param.spec[[1]]) # AIC y BIC de acuerdo con el orden

     ORDER       AIC       BIC
[1,]     0 272.69370 210.95532
[2,]     1  82.14840  24.52591
[3,]     2  84.14419  30.63759
[4,]     3  85.59263  36.20192
[5,]     4  80.47156  35.19675
[6,]     5  70.78220  29.62328

head(param.spec[[2]]) # El mejor modelo

           freq       spec
[1,] 0.00000000 0.02544881
[2,] 0.01202405 0.02550050
[3,] 0.02404810 0.02565601
[4,] 0.03607214 0.02591669
[5,] 0.04809619 0.02628472
[6,] 0.06012024 0.02676306

Bondad de ajuste de los modelos AR según el orden p basado en AIC y BIC

En R, el comando spec.ic escoge el mejor rezago de acuerdo a AIC.

C.info<-data.frame(param.spec[[1]])
colnames(C.info)<-c("orden","AIC","BIC")
C.info

   orden         AIC        BIC
1      0 272.6937023 210.955320
2      1  82.1484043  24.525915
3      2  84.1441892  30.637592
4      3  85.5926277  36.201922
5      4  80.4715619  35.196749
6      5  70.7822012  29.623280
7      6  69.5898661  32.546837
8      7  71.5718647  38.644728
9      8  71.4320021  42.620757
10     9  63.2815353  38.586183
11    10  49.9872355  29.407775
12    11  40.7220194  24.258451
13    12  41.0928139  28.745138
14    13  37.0833413  28.851557
15    14   8.7779160   4.662024
16    15   0.0000000   0.000000
17    16   0.4321663   4.548058
18    17   0.8834736   9.115258
19    18   0.9605224  13.308199
20    19   2.9348253  19.398394
21    20   4.7475516  25.327012
22    21   6.7012637  31.396616
23    22   7.1553956  35.966641
24    23   4.6428297  37.569967
25    24   5.8610042  42.904033
26    25   6.5000325  47.658954
27    26   2.8918549  48.166668
28    27   4.2581518  53.648857
29    28   5.5960927  59.102690
30    29   6.3765400  63.999030
31    30   2.6978096  64.436191
32    31   4.6243480  70.478622
33    32   5.9246340  75.894800
34    33   7.6085953  81.694654
35    34   7.6354835  85.837434
36    35   4.8817282  87.199571
37    36   3.9962278  90.429962
38    37   5.9223121  96.471939
39    38   6.7647416 101.430260
40    39   3.8167034 102.598114
41    40   4.9371390 107.834442
42    41   6.9361882 113.949383
43    42   6.6242894 117.753377
44    43   8.5812482 123.826228
45    44  10.3970778 129.757949
46    45  12.2889991 135.765763
47    46  14.0998243 141.692480

C.info %>% gather(
  key = "C.Info",
  value = "IC",
  AIC,BIC
) %>% ggplot() +
  geom_line( aes(x = orden, y = IC, group=C.Info,color=C.Info)) + theme_bw()

Paquetes en R

Para replicar los ejemplos de esta presentación, necesitan estos paquetes:

library(ggplot2)
library(forecast)
library(fpp2)
library(astsa)
library(tidyverse)

Tema 1: Análisis espectral de series temporales(4)

Estimación espectral no paramétrica

Estimación espectral no paramétrica

Núcleo de Danniell

Ejemplo: SOI y reclutamiento

Espectro logarítmico

Ejemplo: Armónicos

Estimación espectral no paramétrica (extensión)

Estimación espectral no paramétrica (extensión)

Alternativas de núcleos

Ejemplo: SOI y reclutamiento

Estimación espectral paramétrica

Estimación espectral paramétrica

Ejemplo

Paquetes en R

Tema 1: Análisis espectral de series temporales⁽⁴⁾