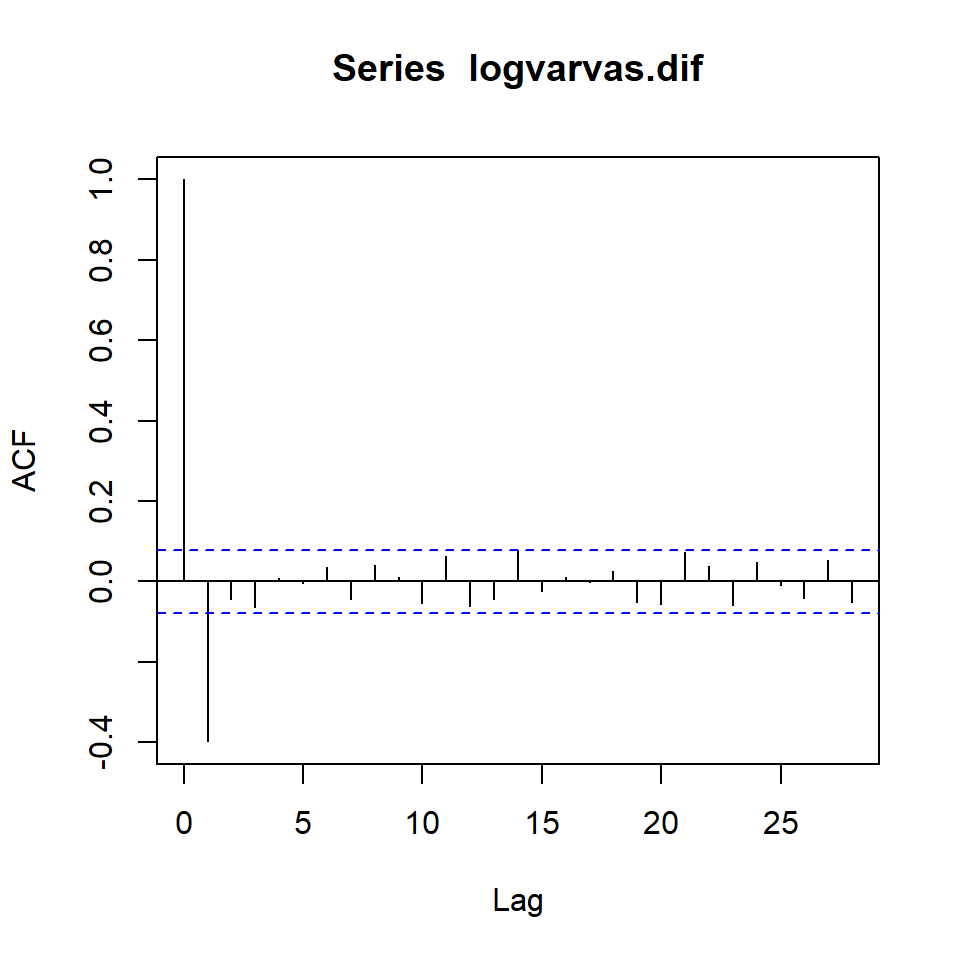Tema 2: Análisis multivariado de series temporales(4)
Procesos integrados
Contenido
Procesos integrados
Serie estacionaria por tendencia y por diferencia
El contraste de raíz unitaria
Ejemplo
Procesos integrados
Considere una serie univariada \(X_t\).
Definición 1 (Proceso integrado) Si \(\nabla^d X_t\) es estacionario, decimos que \(X_t\) es integrado de orden \(d\), y es denotado por \(X_t \sim I(d)\).
Ejemplo 1
Si \(\nabla^d X_t \sim ARMA(p,q)\), decimos que \(X_t\) es ARIMA(p,d,q), o bien \(X_t \sim I(d)\).
Cualquier serie temporal estacionaria es \(I(0)\).
Recuerde la diferenciación estacional \(\nabla_s^D X_t=(1-B^s)^D X_t\)
Definición 2 (Proceso integrado estacionalmente) Si \(\nabla^d \nabla_s^D X_t\) es estacionario, decimos que \(X_t\) es estacionalmente integrado de orden \(d\) y \(D\), y es denotado por \(X_t \sim I(d,D)\).
Ejemplo 2
- Si \(\nabla^d \nabla_s^D X_t \sim ARMA(p,q)\), entonces \(X_t\) es \(SARIMA(p,d,q)(0,D,0)_s\). Decimos que \(X_t \sim I(d,D)\).
Serie estacionaria por tendencia y por diferencia
Contenido
Procesos integrados
Serie estacionaria por tendencia y por diferencia
El contraste de raíz unitaria
Ejemplo
Serie estacionaria por tendencia y por diferencia
Suponga que una serie temporal \(\left\lbrace X_t \right\rbrace\) es una realización de una tendencia determinística y un componente estocástico: \[X_t=CD_t+ \eta_t,\] donde \(CD_t=\beta_0+\beta_1 t\) y \(\eta_t \sim ARMA(p,q)\) que no necesariamente es estacionario e invertible, i.e., tiene su representación \[\phi(B)\eta_t=\theta(B)\epsilon_t\]
Caso 1: Si todas las raíces de \(\phi(B)\) están fuera del circulo unitario, \(\left\lbrace X_t \right\rbrace\) es estacionaria alrededor de una tendencia determinística. Por lo tanto, se puede eliminar la tendencia de la serie original y ajustar un modelo ARMA a los residuales. Este caso se dice que el modelo es estacionario por tendencia (trend-stationary).
Caso 2: si existe una raíz que está exactamente en el círculo unitario y el resto de las raíces están fuera del círculo unitario, i.e. \(\phi(B)=(1-B)\phi^*(B)\), y \(\phi^*(B)\eta_t\) es estacionario, por ende, \(\left\lbrace X_t \right\rbrace\) es estacionaria por diferencia. Por lo tanto, se puede realizar diferenciación para obtener una serie estacionaria. Caso más común es cuando \(d=1\). Este caso se dice que el modelo es estacionario por diferencia (difference-stationary).
Note que el componente del error es \(I(1)\), i.e. ARIMA(p,1,q): \[\phi^*(B)(1-B)\eta_t=\theta(B)\epsilon_t\] Si aplicamos la diferenciación a \[X_t=\beta_0+\beta_1 t+ \eta_t,\] Tenemos que \(\nabla X_t\) es estacionario, pues
\[X_t-X_{t-1}=\beta_0+\beta_1 t+ \eta_t - [\beta_0+\beta_1 (t-1)+ \eta_{t-1}]\] \[=\beta_1 + [\eta_t-\eta_{t-1}]\]
Ejemplo: Tendencia determinística y estocástica
Ajuste con tendencia determinística
Series: austa
Regression with ARIMA(2,0,0) errors
Coefficients:
ar1 ar2 intercept xreg
1.1127 -0.3805 0.4156 0.1710
s.e. 0.1600 0.1585 0.1897 0.0088
sigma^2 = 0.02979: log likelihood = 13.6
AIC=-17.2 AICc=-15.2 BIC=-9.28\[X_t=0.416+0.171t+\eta_t\] \[\eta_t=1.113\eta_{t-1}-0.380 \eta_{t-2}+\epsilon_t\] \[\epsilon_t \overset{iid}{\sim} N(0,0.03)\]
Ajuste con tendencia estocástica
Series: austa
ARIMA(0,1,1) with drift
Coefficients:
ma1 drift
0.3006 0.1735
s.e. 0.1647 0.0390
sigma^2 = 0.03376: log likelihood = 10.62
AIC=-15.24 AICc=-14.46 BIC=-10.57\[X_t-X_{t-1}=0.173+\eta'_t,\] o de otra forma,
\[X_t=X_0+0.173t+\eta_t\] \[\eta_t=\eta_{t-1}+0.301\epsilon_{t-1}+\epsilon_t\] \[\epsilon_t \overset{iid}{\sim} N(0,0.034)\]
fc1 <- forecast::forecast(fit1,
xreg = length(austa) + 1:10)
fc2 <- forecast::forecast(fit2, h=10)
autoplot(austa) +
autolayer(fc2, series="Stochastic trend") +
autolayer(fc1, series="Deterministic trend") +
ggtitle("Forecasts from trend models") +
xlab("Year") + ylab("Visitors to Australia (millions)") +
guides(colour=guide_legend(title="Forecast"))+
theme_bw()+ theme(legend.position="top")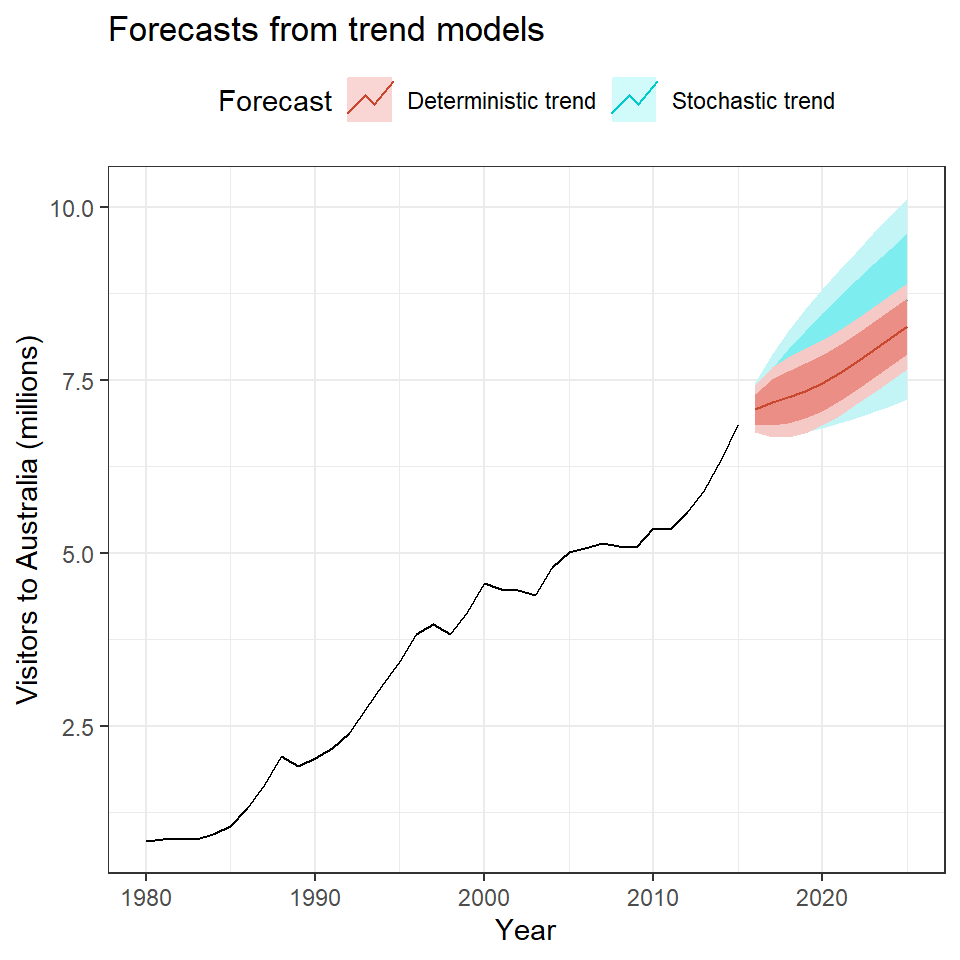
Serie estacionaria por tendencia y por diferencia
- Ejemplo de estos dos tipos de estacionariedad:
Tendencia determinística: \[X_t=X_{t-1}+\mu=X_0+\mu t\] Tendencia estocástica (acumulación de choques aleatorias): \[X_t=X_{t-1}+\epsilon_t=X_0+\sum_{s=1}^t \epsilon_s\] donde \(\mu\) es una constante y \(\epsilon_t\) es ruido blanco.
- En síntesis, una serie temporal \(\left\lbrace X_t \right\rbrace\) está compuesto por una tendencia determinística y un componente estocástico \(\eta_t\) que es modelado por \(ARIMA(p,d,q)\).
- Se puede descomponer \(\eta_t\) en dos componentes: tendencia estocástica (choques aleatorios) y el componente aleatorio “estacionario”.
- Entonces, \(\left\lbrace X_t \right\rbrace\) se puede descomponer en tres componentes:
- tendencia determinística,
- tendencia estocástica, y
- el componente “aleatorio”.
- Un modelo estacionario por tendencia, no tiene la tendencia estocástica, y el componente aleatorio es \(ARMA(p,q)\).
- En el caso de un modelo estacionario por diferencia, el polinomio autoregresivo del componente \(\eta_t\) tiene al menos una raíz unitaria.
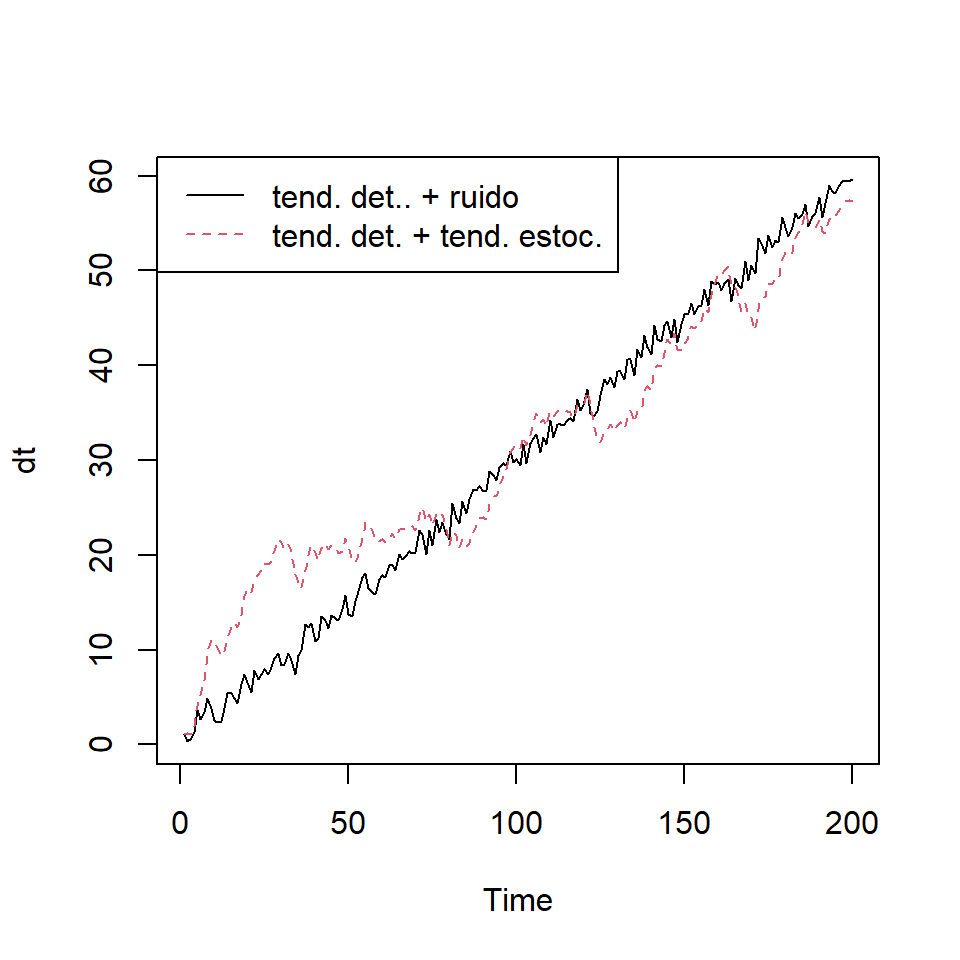
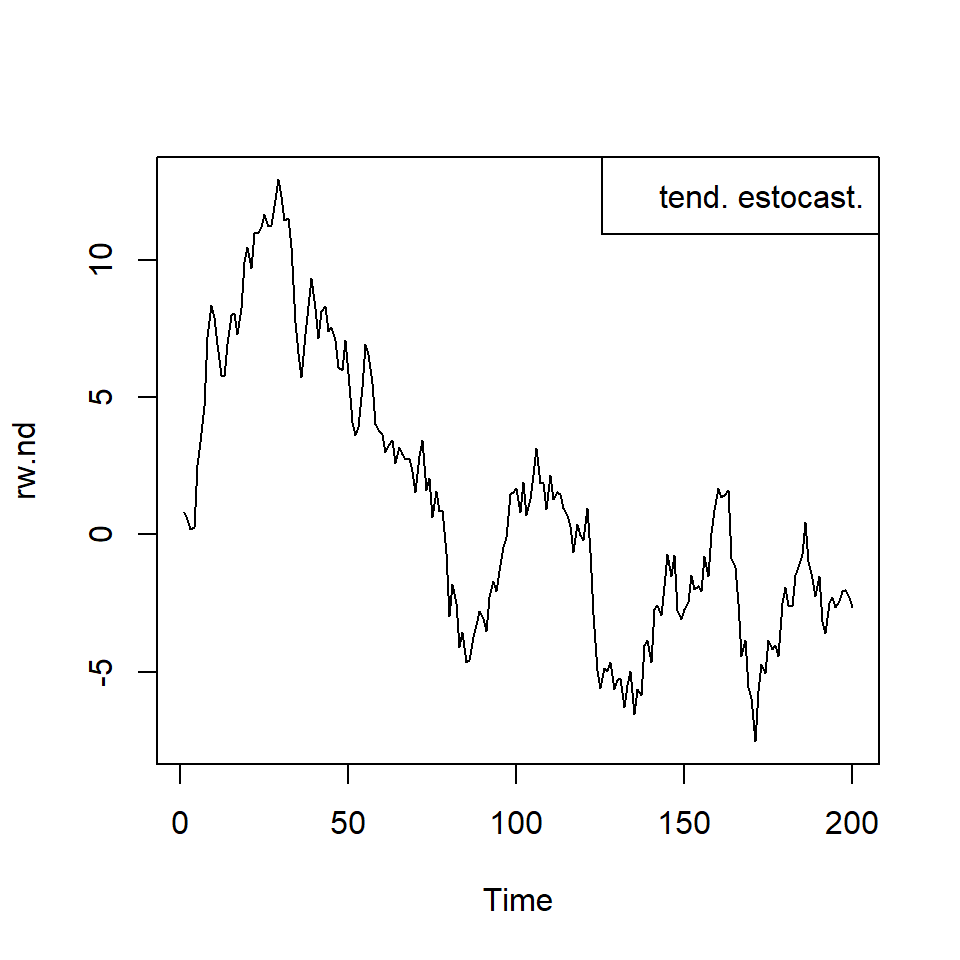
- Vimos que si una serie temporal \(\left\lbrace X_t \right\rbrace\) se puede descomponer en tres componentes: (1) tendencia determinística, (2) tendencia estocástica, y (3) el componente “aleatorio”, i.e., \[ X_t=CD_t+ \eta_t, \] donde \(CD_t=\beta_0+\beta_1 t\) y \(\eta_t \sim ARMA(p,q)\) que no necesariamente es estacionario e invertible, i.e., tiene su representación \[\phi(B)\eta_t=\theta(B)\epsilon_t\]
- Si existe una raíz que está exactamente en el círculo unitario y el resto de las raíces están fuera del círculo unitario, i.e. \(\phi(B)=(1-B)\phi^*(B)\), y \(\phi^*(B)\eta_t\) es estacionario. Por lo tanto, \(\left\lbrace X_t \right\rbrace\) es estacionaria por diferencia. Por lo tanto, se puede realizar diferenciación para obtener una serie estacionaria.
- El modelo se puede representar como \[X_t=CD_t+ \eta_t,\] \[\phi^*(B)(1-B)\eta_t=\theta(B)\epsilon_t\]
El contraste de raíz unitaria
Contenido
Procesos integrados
Serie estacionaria por tendencia y por diferencia
El contraste de raíz unitaria
Ejemplo
El contraste de raíz unitaria
Para investigar si el proceso: \[\eta_t=X_t-CD_t,\] contiene raíz unitaria, Dickey Fuller (1979) propuso la prueba de DF de la siguiente forma:
- Suponiendo que \(\eta_t\) es un AR(1):
\[\eta_t=\phi_1 \eta_{t-1}+a_t\]
- Si se toma una diferencia:
\[\nabla \eta_t=\eta_t-\eta_{t-1}=\phi_1 \eta_{t-1}+a_t-\eta_{t-1}=(\phi_1-1) \eta_{t-1}+a_t=\pi \eta_{t-1}+a_t\]
Se puede obtener el estimador del mínimo cuadrado de \(\hat{\pi}^*\) mediante una regresión ordinaria de \(\nabla \eta_t\) sobre \(\eta_{t-1}\). Por lo tanto, el contraste para la estacionariedad se puede formular mediante las siguientes hipótesis: \[H_0: \phi_1=1 ~~\text{v.s.}~~ H_1: \phi_1<1\]
- De la diapositiva anterior,
\[\nabla \eta_t=\eta_t-\eta_{t-1}=\phi_1 \eta_{t-1}+a_t-\eta_{t-1}=(\phi_1-1) \eta_{t-1}+a_t=\pi \eta_{t-1}+a_t\]
La idea es obtener el estimador del mínimo cuadrado de \(\hat{\pi}\) mediante una regresión ordinaria de \(\nabla \eta_t\) sobre \(\eta_{t-1}\). Por lo tanto, el contraste para la estacionariedad se puede formular mediante las siguientes hipótesis: \[H_0: \phi_1=1 ~~\text{v.s.}~~ H_1: \phi_1<1\] o equivalentemente a: \[H_0: \pi=0 ~~\text{v.s.}~~ H_1: \pi<0\]
- El contraste se puede realizar mediante la estadística \(\hat{\tau}\) de Dickey-Fuller:
\[\hat{\tau}=\frac{\hat{\pi}^*}{e.e.(\hat{\pi}^*)}.\]
- La distribución de \(\hat{\tau}\) no es conocida y se obtiene los percentiles y los valores críticos de la distribución de \(\hat{\tau}\) por medio de simulaciones.
- Si se rechaza la \(H_0\), la serie es estacionaria.
- Si no se rechaza la \(H_0\), la serie es no estacionaria, y se tiene que: \[\eta_t-\eta_{t-1}=a_t,\] la cual es denominada camino aleatorio.
El procedimiento anterior realiza la prueba después de remover el componente de tendencia determinística \(CD_t\), y además, considera un caso simple de AR(1).
Se puede generalizar el procedimiento anterior involucrando la tendencia determinística y el componente aleatorio de AR(p) y es llamado como prueba de Dickey-Fuller aumentado. Considere
\[\nabla X_t= \tau' DR_t + \pi X_{t-1} + \sum_{j=1}^{k} \gamma_j \nabla X_{t-j} +a_t,~~\text{con}~~ k=p-1\] para asegurar que la correlación serial en el error es removido.
- Este procedimiento involucra un valor \(k\) predeterminado.
- Considere el caso de una tendencia lineal: \[\nabla X_t= \beta_0 + \beta_1 t + \pi X_{t-1} + \sum_{j=1}^{k} \gamma_j \nabla X_{t-j} +a_t,~~\text{con}~~ k=p-1\] para asegurar que la correlación serial en el error es removido.
Paso 1: Probar \(H_0: \pi=0\) (con el estadístico \(\tau\))
- Si se rechaza \(H_0\), entonces no hay raíz unitaria.
Paso 2: Si \(\pi = 0\), probar \(H_0: \beta_1=\pi=0\) (con el estadístico \(\Phi_3\)).
- Si no se rechaza \(H_0\), entonces no hay tendencia y tiene raíz unitaria.
- Si se rechaza \(H_0\), hay tendencia y tiene raíz unitaria.
Ejemplo
Contenido
Procesos integrados
Serie estacionaria por tendencia y por diferencia
El contraste de raíz unitaria
Ejemplo
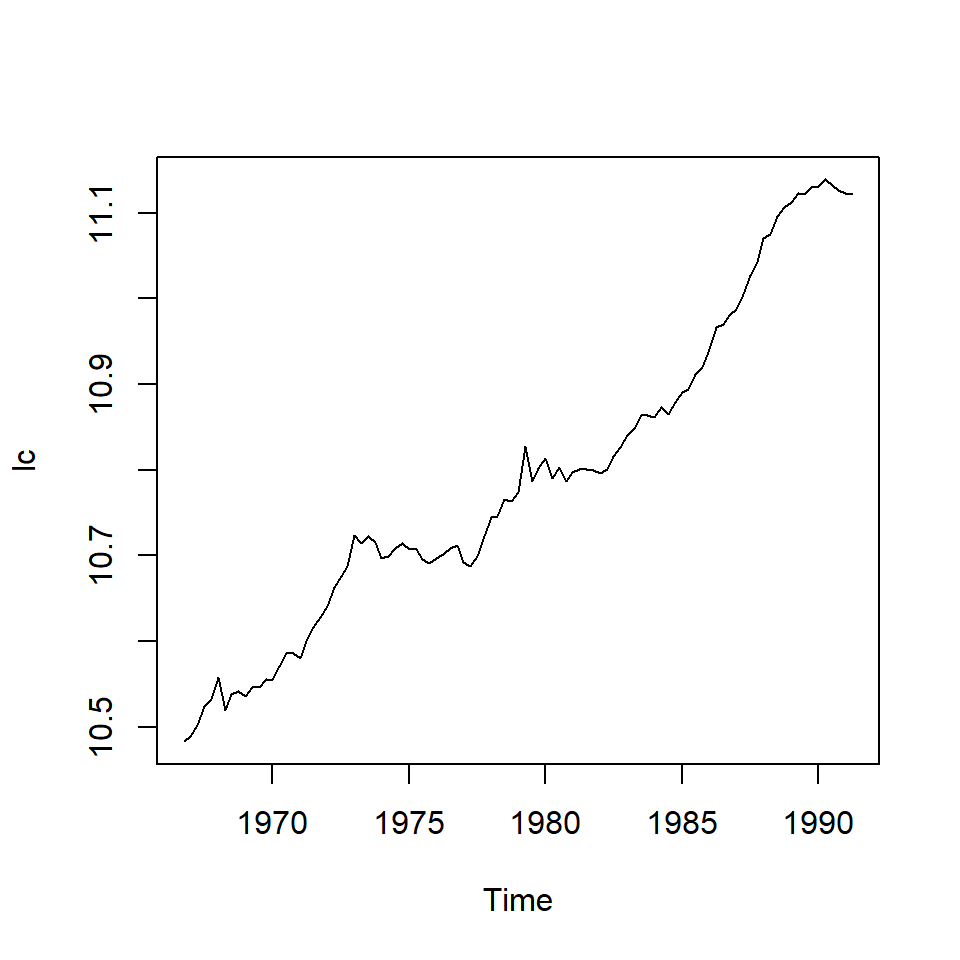
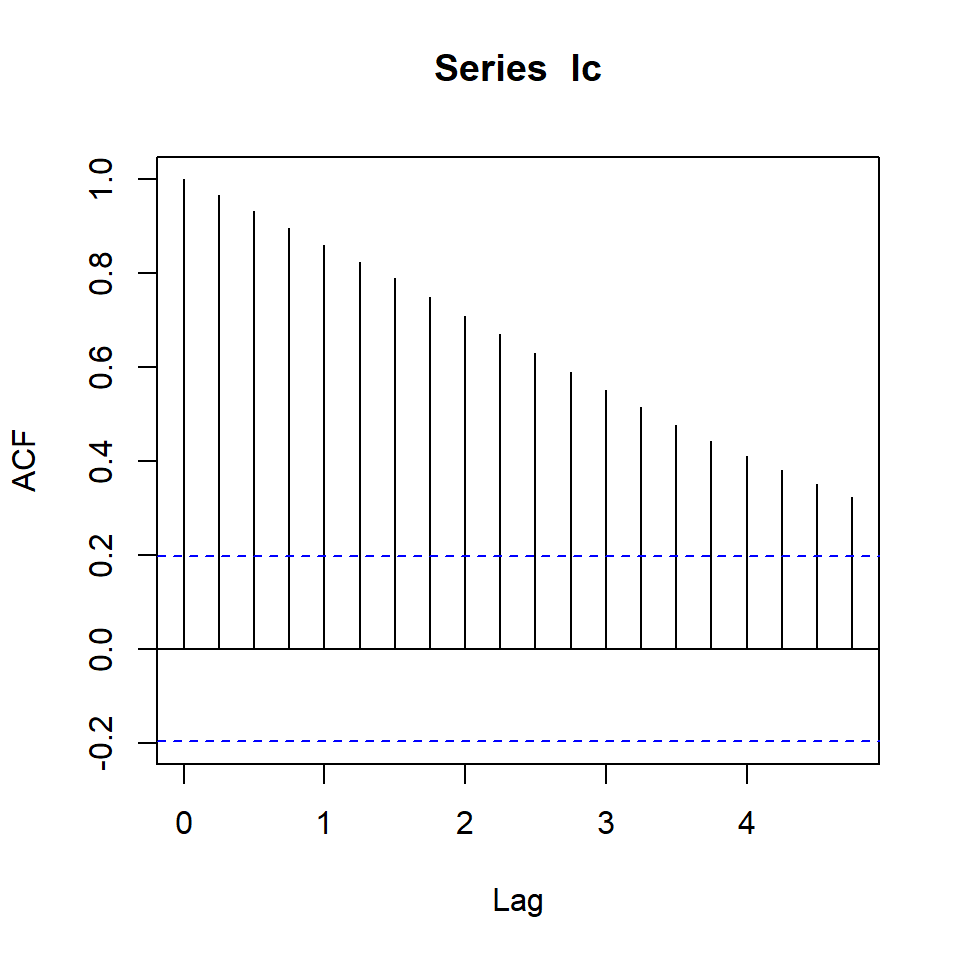
Ejemplo: La serie de consumo
La serie del índice de consumo en Reino Unido del cuarto trimestre, 1966 al segundo trimestre de 1991.
- Contraste de Dickey-Fuller con el paquete
tseries.
###############################################
# Augmented Dickey-Fuller Test Unit Root Test #
###############################################
Test regression trend
Call:
lm(formula = z.diff ~ z.lag.1 + 1 + tt + z.diff.lag)
Residuals:
Min 1Q Median 3Q Max
-0.044714 -0.006525 0.000129 0.006225 0.045353
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 0.7976591 0.3547775 2.248 0.0270 *
z.lag.1 -0.0758706 0.0338880 -2.239 0.0277 *
tt 0.0004915 0.0002159 2.277 0.0252 *
z.diff.lag1 -0.1063957 0.1006744 -1.057 0.2934
z.diff.lag2 0.2011373 0.1012373 1.987 0.0500 .
z.diff.lag3 0.2998586 0.1020548 2.938 0.0042 **
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 0.01307 on 89 degrees of freedom
Multiple R-squared: 0.1472, Adjusted R-squared: 0.09924
F-statistic: 3.071 on 5 and 89 DF, p-value: 0.01325
Value of test-statistic is: -2.2389 3.7382 2.5972
Critical values for test statistics:
1pct 5pct 10pct
tau3 -4.04 -3.45 -3.15
phi2 6.50 4.88 4.16
phi3 8.73 6.49 5.47Paso 1: Probar \(H_0: \pi=0\) (con el estadístico \(\tau\))
- Usando un 5% de significancia, note que el valor crítico es \(-3.45<-2.2389\) el estadístico \(\tau\). Por lo tanto, no se rechaza \(H_0\).
Paso 2: Dado que \(\pi=0\), probamos \(H_0: \beta_1=\pi=0\) (con el estadístico \(\Phi_3\)).
- Note que el estadístico \(F\)= \(2.5972<6.49\) el valor crítico. Por lo tanto, no se rechaza \(H_0\).
- Se concluye que el modelo no tiene tendencia, y con raíz unitaria.
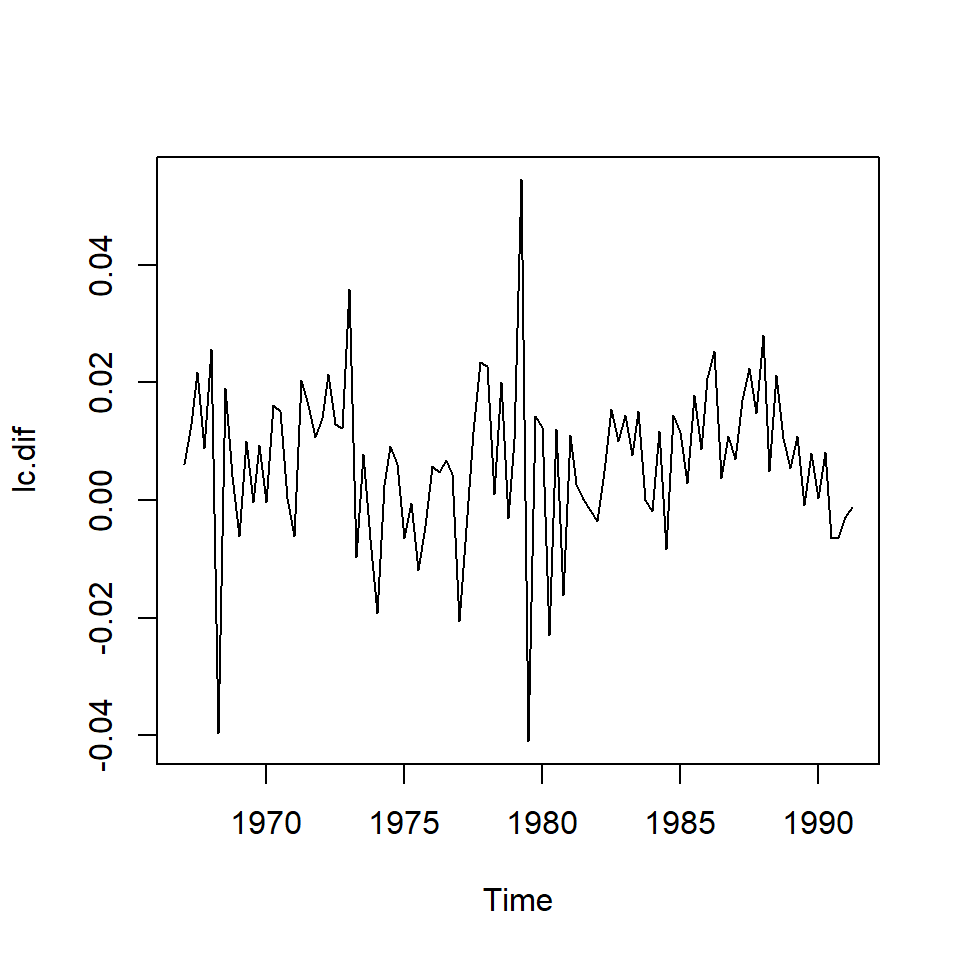
Paso 3: Ya que la serie contiene raíz unitaria, se realiza diferenciación para analizarlo.
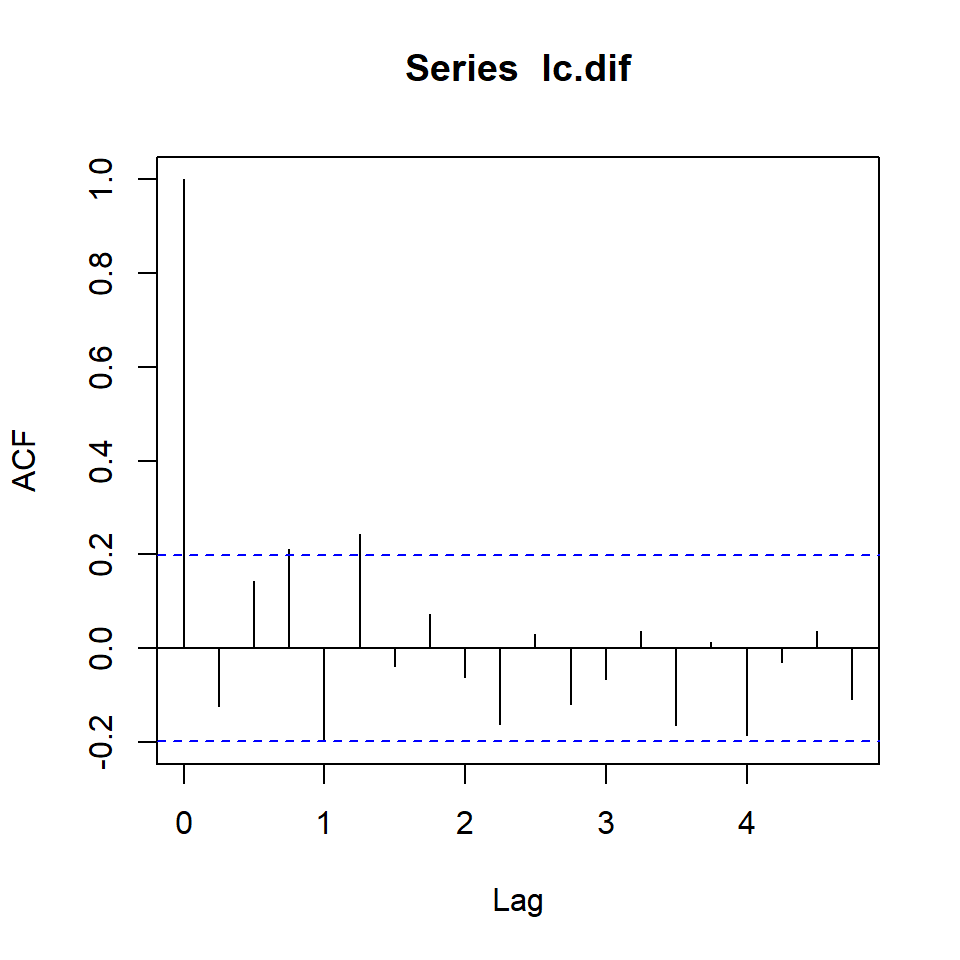
La serie diferenciada:
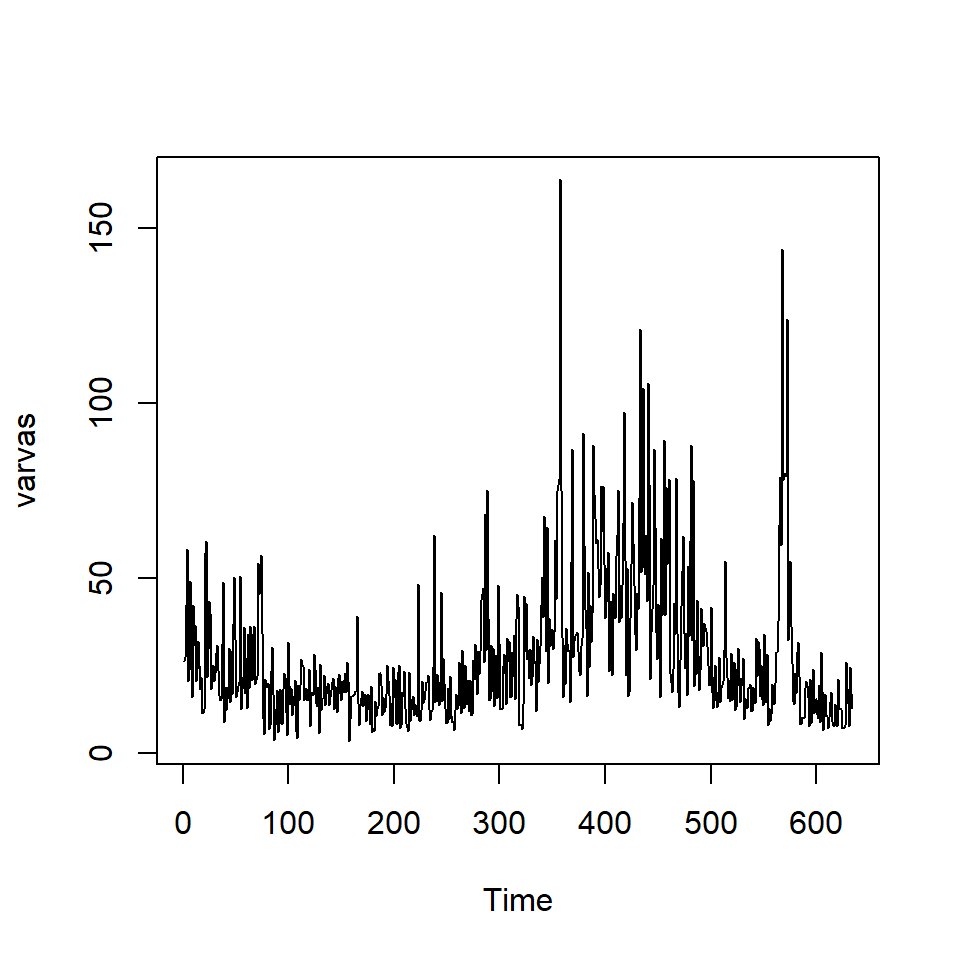
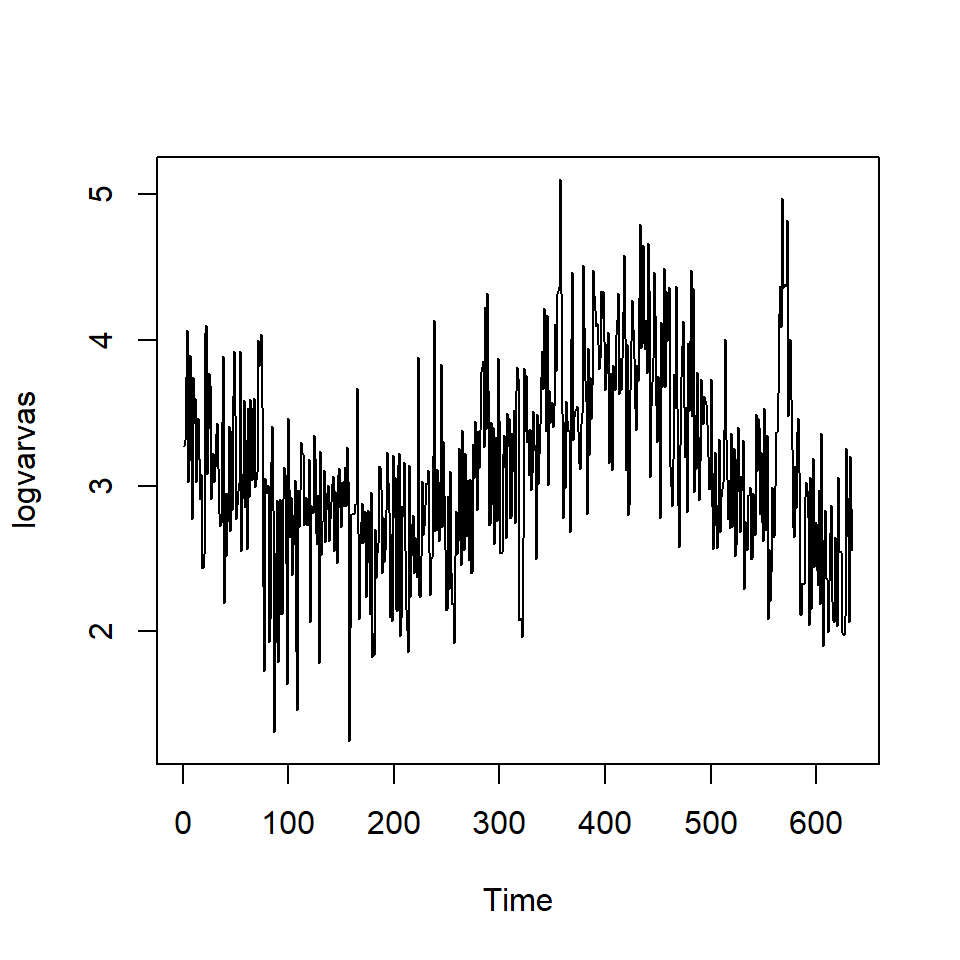
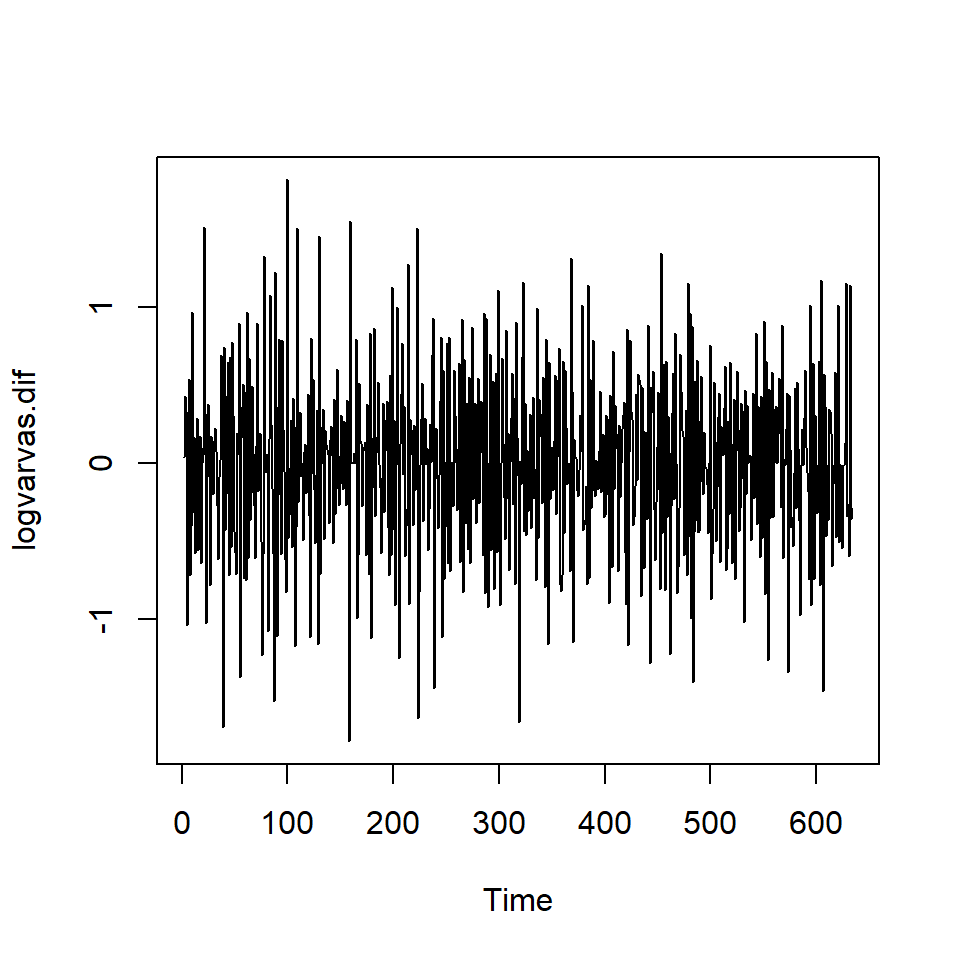
Ejemplo: La serie de varvas
Los glaciares que se derriten depositan capas anuales de arena y limo durante las temporadas de derretimiento de primavera, que pueden reconstruirse anualmente durante un período que va desde el momento en que comenzó la desglaciación en Nueva Inglaterra (hace unos 12.600 años) hasta el momento en que terminó (hace unos 6000 años). Dichos depósitos sedimentarios, llamados varvas, pueden utilizarse como sustitutos de parámetros paleoclimáticos, como la temperatura, porque, en un año cálido, se depositan más arena y limo del glaciar en retroceso.
- Contraste de Dickey-Fuller con el paquete
tseries.
###############################################
# Augmented Dickey-Fuller Test Unit Root Test #
###############################################
Test regression trend
Call:
lm(formula = z.diff ~ z.lag.1 + 1 + tt + z.diff.lag)
Residuals:
Min 1Q Median 3Q Max
-1.81723 -0.33265 0.02373 0.32042 1.35376
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 0.6719323 0.1198531 5.606 3.11e-08 ***
z.lag.1 -0.2296531 0.0383667 -5.986 3.63e-09 ***
tt 0.0001277 0.0001088 1.173 0.241
z.diff.lag1 -0.3866604 0.0466622 -8.286 7.15e-16 ***
z.diff.lag2 -0.2397781 0.0454677 -5.274 1.85e-07 ***
z.diff.lag3 -0.1624700 0.0395751 -4.105 4.57e-05 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 0.4883 on 624 degrees of freedom
Multiple R-squared: 0.2905, Adjusted R-squared: 0.2848
F-statistic: 51.09 on 5 and 624 DF, p-value: < 2.2e-16
Value of test-statistic is: -5.9857 11.9565 17.9168
Critical values for test statistics:
1pct 5pct 10pct
tau3 -3.96 -3.41 -3.12
phi2 6.09 4.68 4.03
phi3 8.27 6.25 5.34Paso 1: Probar \(H_0: \pi=0\) (con el estadístico \(\tau\))
- Usando un 5% de significancia, note que el valor crítico es \(-3.96>-5.9857\) el estadístico \(\tau\). Por lo tanto, se rechaza \(H_0\).
- Si excluimos la tendencia, los resultados son diferentes:
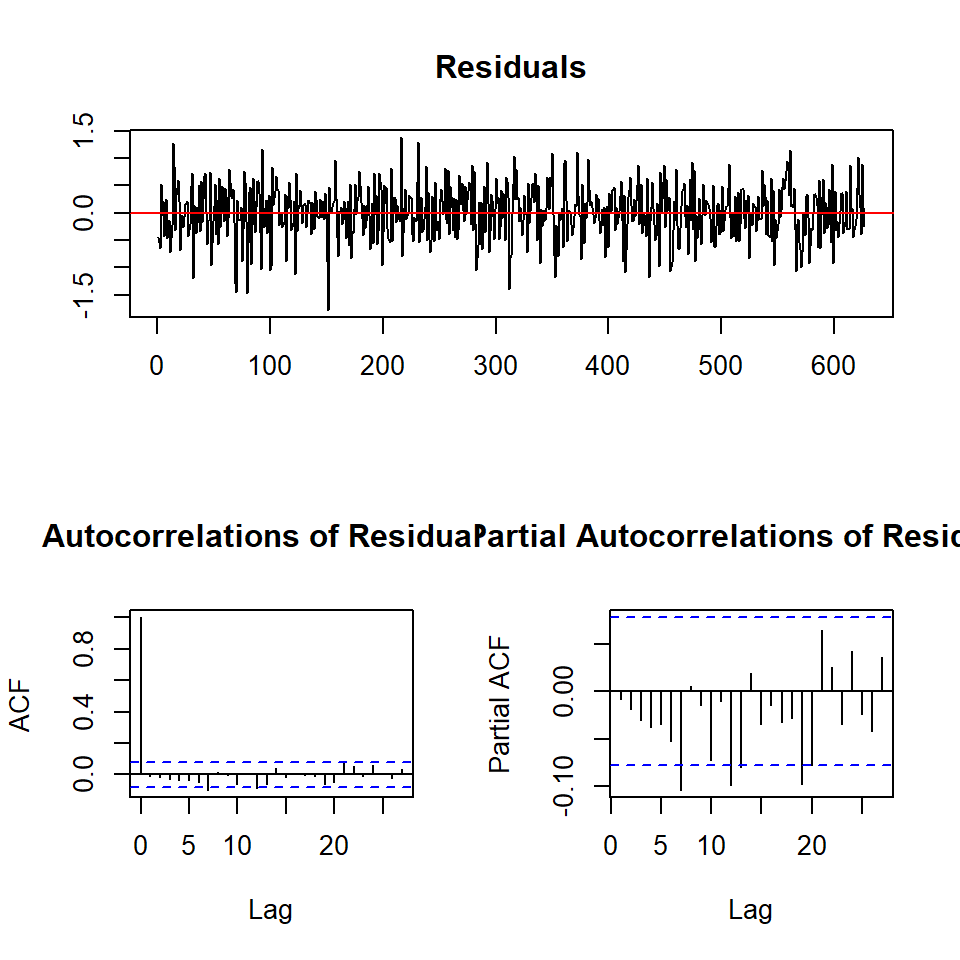
- Si excluimos la tendencia, los resultados son diferentes:
###############################################
# Augmented Dickey-Fuller Test Unit Root Test #
###############################################
Test regression none
Call:
lm(formula = z.diff ~ z.lag.1 - 1 + z.diff.lag)
Residuals:
Min 1Q Median 3Q Max
-1.78375 -0.30973 0.03514 0.32733 1.38755
Coefficients:
Estimate Std. Error t value Pr(>|t|)
z.lag.1 -0.005218 0.006166 -0.846 0.3977
z.diff.lag1 -0.621933 0.040278 -15.441 < 2e-16 ***
z.diff.lag2 -0.477643 0.046705 -10.227 < 2e-16 ***
z.diff.lag3 -0.414364 0.048999 -8.457 < 2e-16 ***
z.diff.lag4 -0.299850 0.048991 -6.120 1.65e-09 ***
z.diff.lag5 -0.197807 0.046575 -4.247 2.50e-05 ***
z.diff.lag6 -0.080740 0.040033 -2.017 0.0441 *
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 0.4873 on 620 degrees of freedom
Multiple R-squared: 0.2928, Adjusted R-squared: 0.2848
F-statistic: 36.68 on 7 and 620 DF, p-value: < 2.2e-16
Value of test-statistic is: -0.8463
Critical values for test statistics:
1pct 5pct 10pct
tau1 -2.58 -1.95 -1.62- Usando un 5% de significancia, note que el valor crítico es \(-2.58>-0.8463\) el estadístico \(\tau\). Por lo tanto, no se rechaza \(H_0\) y se concluye que hay raíz unitaria.
La serie diferenciada:
Otros contrastes de raíz unitaria
- Prueba de Phillips-Perron
- Prueba de Elliott-Rothenberg-Stock
- Prueba de Schmidt-Phillips
- Prueba de Kwiatkowski-Phillips-Schmidt-Shin
Paquetes en R
Para replicar los ejemplos de esta presentación, necesitan estos paquetes: