Tema 3: Modelos de Espacio-Estado⁽²⁾

Curso: Tópicos Avanzados de Series Temporales

Shu Wei Chou Chen

shuwei.chou@ucr.ac.cr

Escuela de Estadística, Universidad de Costa Rica

Introducción

Contenido

Introducción
El paquete dlm: funciones básicas
DLM de primer orden (Modelo de nivel local)
DLM de segundo orden
Ejemplo: AR(1)
Combinación de modelos de espacio de estados

Introducción

Existe una variedad de literatura y paquetes en R para tratar los modelos de espacio de estados.
Paquetes generales que proporciona estimación máxima verosimilitud, filtro de Kalman y estimación Bayesiana para DLM o modelos de espacio de estados lineal Gaussiano:
- astsa
- dlm
- KFAS: Modelo de espacio de estados con familia exponencial.
- mvgam: GAM dinámico y espacio de estados.
- statespacer
- bsts: Modelos estructurales de series temporales Bayesianos.
La dificultad de que cada referencia usa una notación diferente, pero la estructura del modelo es la misma.
Una buena referencia que resume las diferencias y ventajas de algunos paquetes: State Space Models in R

Concentramos en el paquete dlm
- La ecuación de observaciones: \(~~~~y_{t}=F_t \theta_{t} + v_{t},\)
- La ecuación de estados: \(~~~~~~~~~~~~~\theta_{t}=G_t \theta_{t-1} + w_{t},\)

para \(t=1,...,n,\) con la condición inicial \(\theta_0 \sim N_p(m_0,C_0)\).

Las variables de estado \(\theta_t\) son vectores \(p \times 1\) autoregresivos de orden 1, y las observaciones \(y_t\) son vectores \(m \times 1\).
- \(F_t\) y \(G_t\) son matrices \(m\times p\) y \(p\times p\), respectivamente.
- \(v_t\) es ruido \(q\times 1\) tal que \(v_t \overset{iid}{\sim} N_m(0,V_t)\).
- \(w_t\) es un vector \(p\times 1\) tal que \(w_t \overset{iid}{\sim} N_p(0,W_t)\).

En la práctica, el interéses es estimar el valor de \(\theta_t\) dado los datos observados \(y_{1:s}=\left\lbrace y_1,...,y_s \right\rbrace\).
La estimación de \(\theta_t\) se puede clasificar en 3 situaciones:
1. Cuando \(s<t\), el problema es llamado pronóstico o predicción.
2. Cuando \(s=t\), el problema es llamado filtración.
3. Cuando \(s>t\), el problema es llamado suavizamiento.

El paquete `dlm`: funciones básicas

Contenido

Introducción
El paquete dlm: funciones básicas
DLM de primer orden (Modelo de nivel local)
DLM de segundo orden
Ejemplo: AR(1)
Combinación de modelos de espacio de estados

El paquete `dlm`: funciones básicas

La ecuación de observaciones:

\[y_{t}=F_t \theta_{t} + v_{t},~~v_t \overset{iid}{\sim} N_m(0,V_t)\]
La ecuación de estados:

\[\theta_{t}=G_t \theta_{t-1} + w_{t},~~w_t \overset{iid}{\sim} N_p(0,W_t)\]

para \(t=1,...,n,\) con la condición inicial \(\theta_0 \sim N_p(m_0,C_0)\).

Parámetro	Argumento de la función
\(F\)	`FF`
\(V\)	`V`
\(G\)	`GG`
\(W\)	`W`
\(C_0\)	`C0`
\(m_0\)	`m0`

Nota

La escogencia de \(F_t\) y \(G_t\) depende del usuario al observar la naturaleza de las series observadas.
La especificación del modelo requiere la descripción de las variancias \(V_t\) y \(W_t\). En la práctica, es común suponer que son constantes en el tiempo, i.e. \(V_t=V\) y \(W_t=W\).

Funciones	Modelo
`dlm`	DLM genérico
`dlmModARMA`	modelo ARMA
`dlmModPoly`	DLM del polinomio del n-ésimo orden
`dlmReg`	Regresión lineal
`dlmSeas`	factores periódicos, o estacionales
`dlmTrig`	funciones periódicas o trigonométricas

funciones	Método
`dlmFilter`	Filtro de Kalman
`dlmSmooth`	Suavizamiento de Kalman
`dlmForecast`	Predicción
`dlmLL`	Función de verosimilitud
`dlmMLE`	Estimación ML

DLM de primer orden (Modelo de nivel local)

Contenido

Introducción
El paquete dlm: funciones básicas
DLM de primer orden (Modelo de nivel local)
DLM de segundo orden
Ejemplo: AR(1)
Combinación de modelos de espacio de estados

DLM de primer orden (Modelo de nivel local)

El modelo de nivel local tiene la siguiente estructura:

\[\left. \begin{eqnarray} y_t& = & \theta_t +v_t, & ~~~v_t \overset{iid}{\sim}N(0,V_t) \\ \theta_t& = & \theta_{t-1} +w_t, &~~~ w_t \overset{iid}{\sim}N(0,W_t) \\ \end{eqnarray}\right.\]

\(\theta_t\) es escalar y \(F_t=G_t=1\).
La ecuación de estados consiste en una caminata aleatoria y la ecuación de observaciones consiste en la suma del componente de tendencia y un ruido.
Observe que la variancia de las observaciones y de los estados puede variar en el tiempo.

Usualmente definimos \(V_t=V\) y \(W_t=W\), entonces para especificar por ejemplo:

\[\left. \begin{eqnarray} y_t& = & \theta_t +v_t, & v_t \overset{iid}{\sim}N(0,0.8) \\ \theta_t& = & \theta_{t-1} +w_t, & w_t \overset{iid}{\sim}N(0,0.1) \\ \end{eqnarray}\right.\]

Usando la función genérica:

dlm(FF = 1, V = 0.8, GG = 1, W = 0.1, m0 = 0, C0 = 100)

O bien usando la función dlmModPoly

dlmModPoly(order = 1, dV = 0.8, dW = 0.1, C0 = 100)

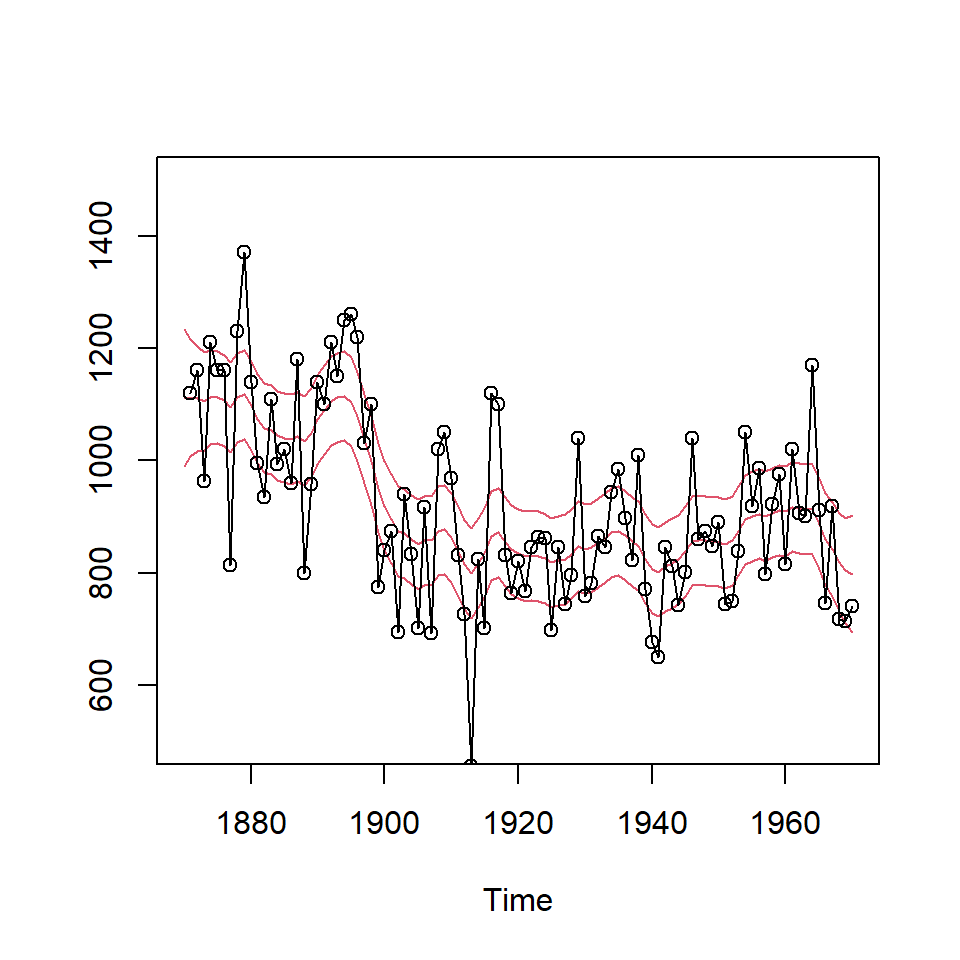
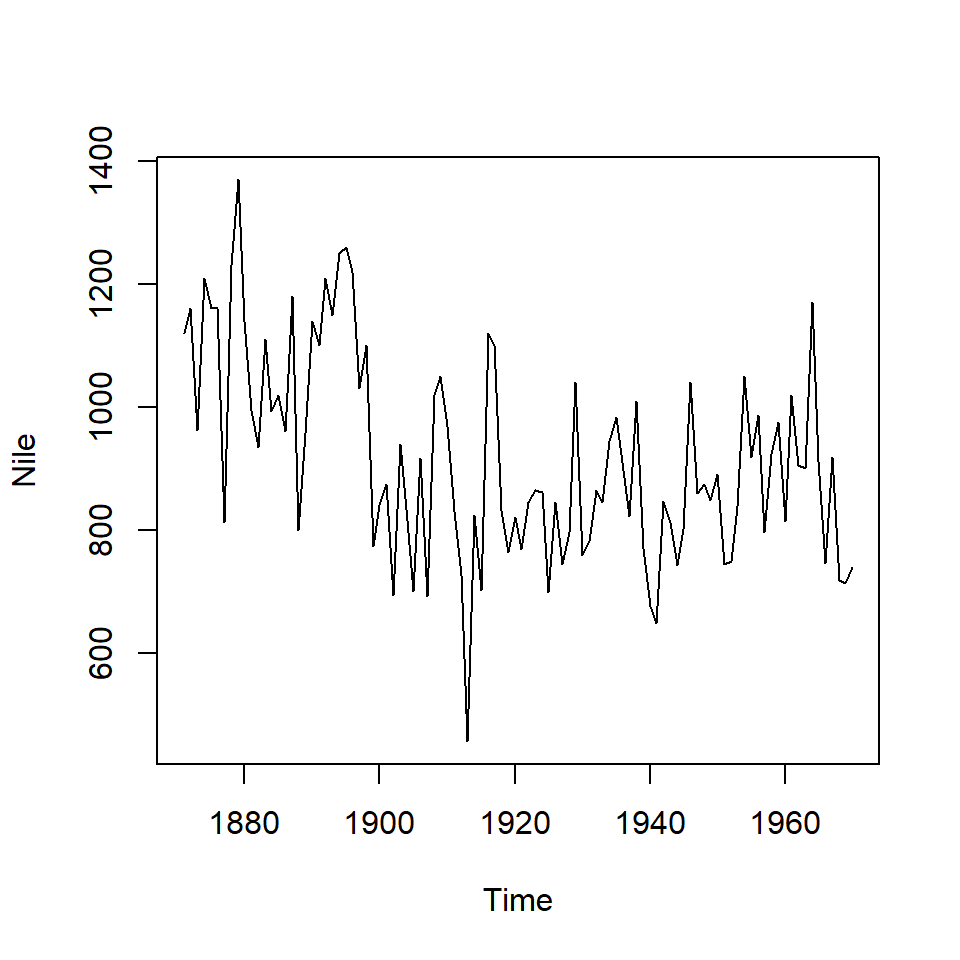
Ejemplo: Caudal anual del Rio Nilo

Mediciones del caudal anual del Nilo en Asuán, Egipto., 1871–1970, en \(10^8 m^3\),

plot(Nile)

dlm.orden1 <- function(theta) {
  dlmModPoly(order = 1, dV = theta[1], dW = theta[2])
}
fit <- dlmMLE(Nile, parm = c(100, 2), dlm.orden1, lower = rep(1e-4, 2))
fit

$par
[1] 15099.787  1468.438

$value
[1] 549.6918

$counts
function gradient 
      32       32 

$convergence
[1] 0

$message
[1] "CONVERGENCE: REL_REDUCTION_OF_F <= FACTR*EPSMCH"

Después de estimar por máxima veroslimitud el modelo de nivel local, se tiene que

\[\hat{V}=15099, \hat{W}=1468\]

modNile <- dlm.orden1(fit$par)
smoothNile <- dlmSmooth(Nile, modNile)

hwidth <- qnorm(0.05, lower = FALSE) *
  sqrt(unlist(dlmSvd2var(smoothNile$U.S, smoothNile$D.S)))
sm <- cbind(smoothNile$s, as.vector(smoothNile$s) + hwidth %o% c(-1, 1))

ts.plot(sm,col=2,ylim=c(500,1500))
lines(Nile, type = 'o')

filterNile <- dlmFilter(Nile, modNile)
plot(residuals(filterNile, sd = FALSE), type = "o",
         ylab = "Standardized prediction error")
abline(h = 0)

tsdiag(filterNile)

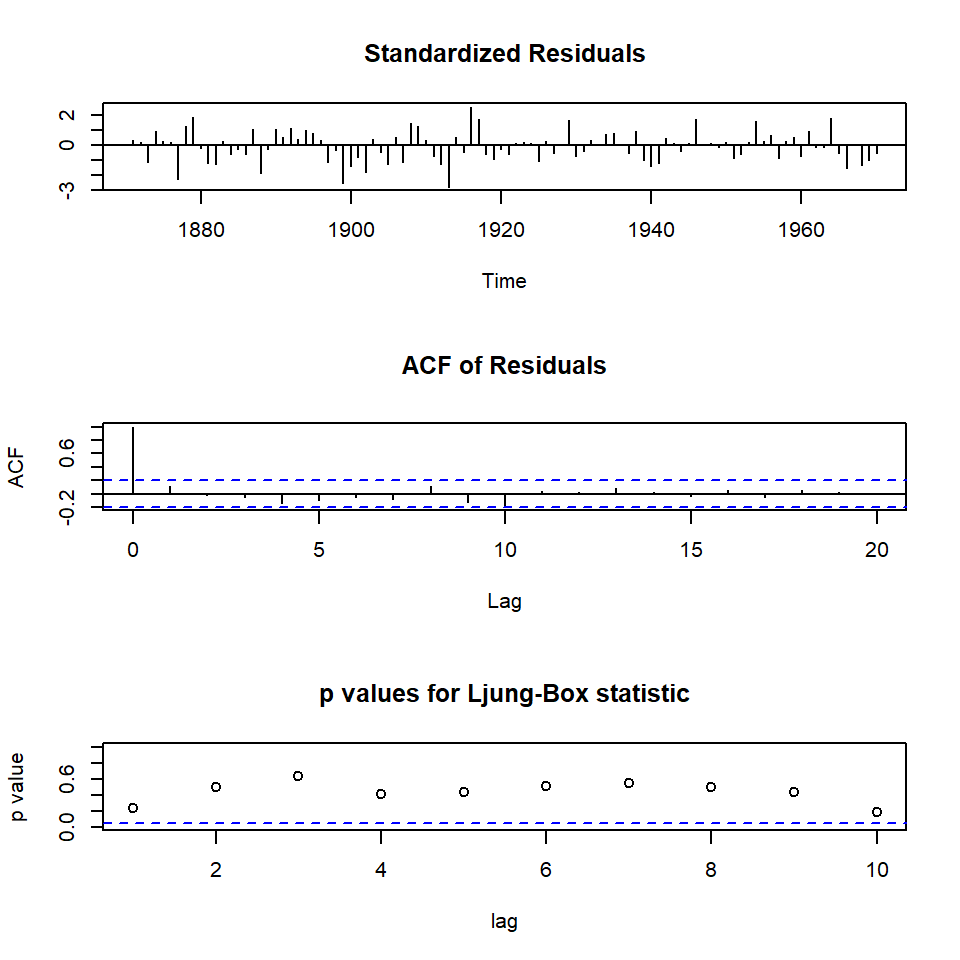
foreNile <- dlmForecast(filterNile, nAhead = 10)
attach(foreNile)
hwidth <- qnorm(0.25, lower = FALSE) * sqrt(unlist(Q))
fore <- cbind(f, as.vector(f) + hwidth %o% c(-1, 1))
rg <- range(c(fore, window(Nile, start = c(1900, 1))))+c(0,300)
plot(fore, type = "o", pch = 16, plot.type = "s", lty = c(1, 3, 3),
         ylab = "Nile level", xlab = "", xlim = c(1900, 1980), ylim = rg)
lines(window(Nile, start = c(1900, 1)), type = 'o')
lines(window(smoothNile$s, start = c(1900,1)), lty = 5)
abline(v = mean(c(time(f)[1], tail(time(Nile), 1))),
           lty = "dashed", col = "darkgrey")
legend("topleft", lty = c(1, 5, 1, 3), pch = c(1, NA, 16, 16), bty = "n",
           legend = c("observed level", "smoothed level", "forecasted level",
                        "50% probability limits"))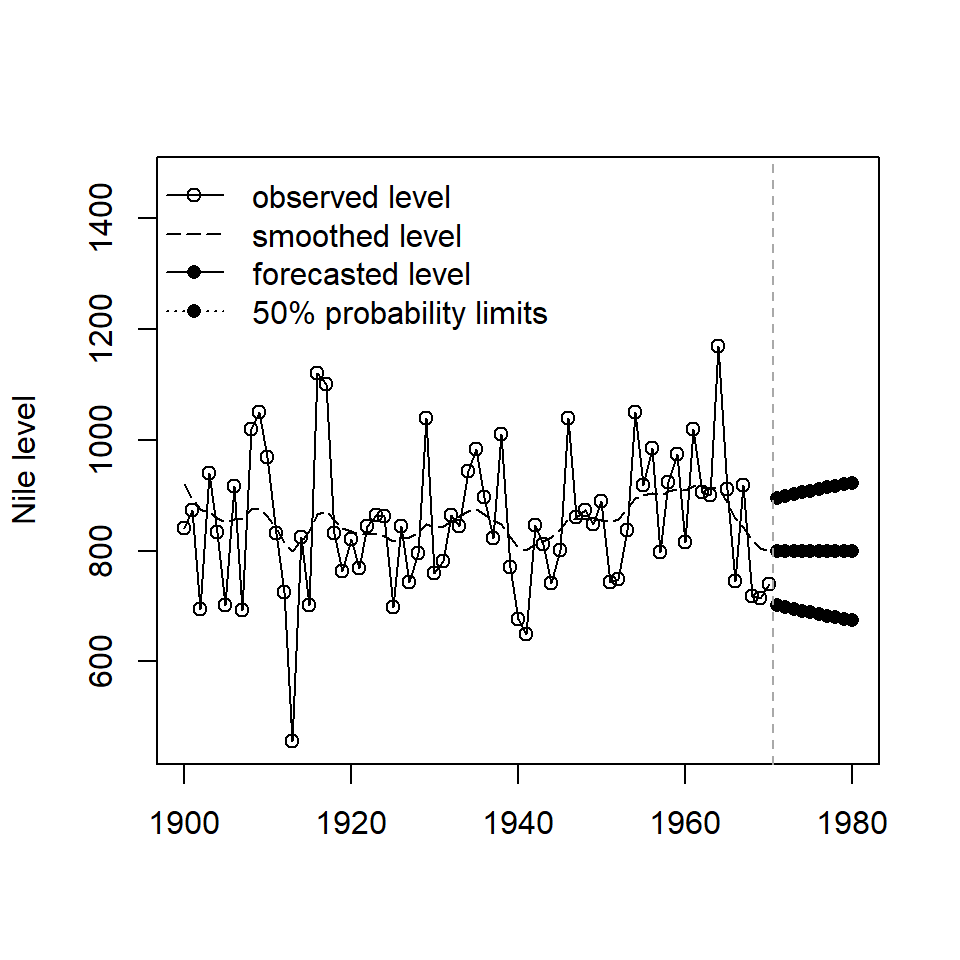

DLM de segundo orden

Contenido

Introducción
El paquete dlm: funciones básicas
DLM de primer orden (Modelo de nivel local)
DLM de segundo orden
Ejemplo: AR(1)
Combinación de modelos de espacio de estados

DLM de segundo orden

El modelo de nivel local tiene la siguiente estructura:

\[\left. \begin{eqnarray} y_t& = & \theta_{1,t} & & +v_t, & &~~~v_t \overset{iid}{\sim}N(0,V_t) \\ \theta_{1,t}& = & \theta_{1,t-1} +&\theta_{2,t-1} & +w_{1,t}, & & \\ \theta_{2,t}& = & & \theta_{2,t-1} & +w_{2,t}, & & ~~~ \\ \end{eqnarray}\right.\]

donde \(w_t=(w_{1,t},w_{2,t})'\overset{iid}{\sim}N(0,W_t)\)

Este modelo se puede escribir con la fórmula general: \[F_t=(1,0),~~~G_t=\begin{bmatrix}1 & 1\\ 0 & 1 \end{bmatrix}\]

Ejemplo: Caudal anual del Rio Nilo

dlm.orden2 <- function(theta) {
  dlmModPoly(order = 2, dV = theta[1], dW = c(theta[2],theta[3]))
}
fit2 <- dlmMLE(Nile, parm = c(1,1,1), dlm.orden2, lower = rep(1e-4,1e-4,1e-4))
fit2

$par
[1]  1.058979e+04  5.639765e+03 -3.464080e-07

$value
[1] 557.4118

$counts
function gradient 
      78       78 

$convergence
[1] 0

$message
[1] "CONVERGENCE: REL_REDUCTION_OF_F <= FACTR*EPSMCH"

modNile2 <- dlm.orden2(fit2$par)
filteredNile <- dlmFilter(Nile, mod = modNile2)
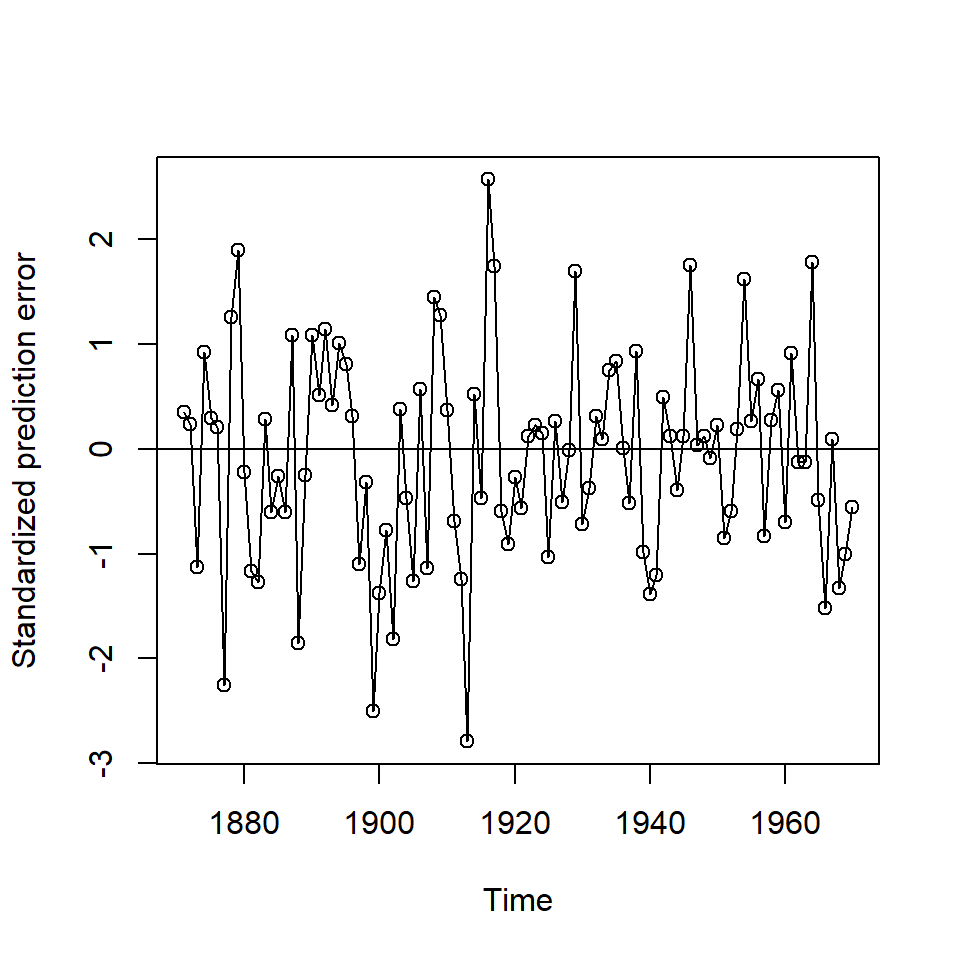
resids <- residuals(filteredNile, sd = FALSE)
smoothNile <- dlmSmooth(Nile, modNile2)

theta1 <- dropFirst(smoothNile$s[, 1])
theta2 <- dropFirst(smoothNile$s[, 2])

par(mfrow = c(3, 1), mar = c(2.2, 2.2, 1, 1), cex = 0.8)
plot.ts(Nile, col = "darkgrey", xlab = "", ylab = "", lwd = 2)
lines(theta1, col = "black")
legend("topright", legend = c("Observación", "Estado"), 
       lwd = c(2, 1), col = c("darkgrey", "black"), bty = "n")

plot.ts(theta2, col = "darkgrey", xlab = "", ylab = "", 
        lwd = 2)
legend("topright", legend = "Pendiente", lwd = 2, col = "darkgrey", 
       bty = "n")
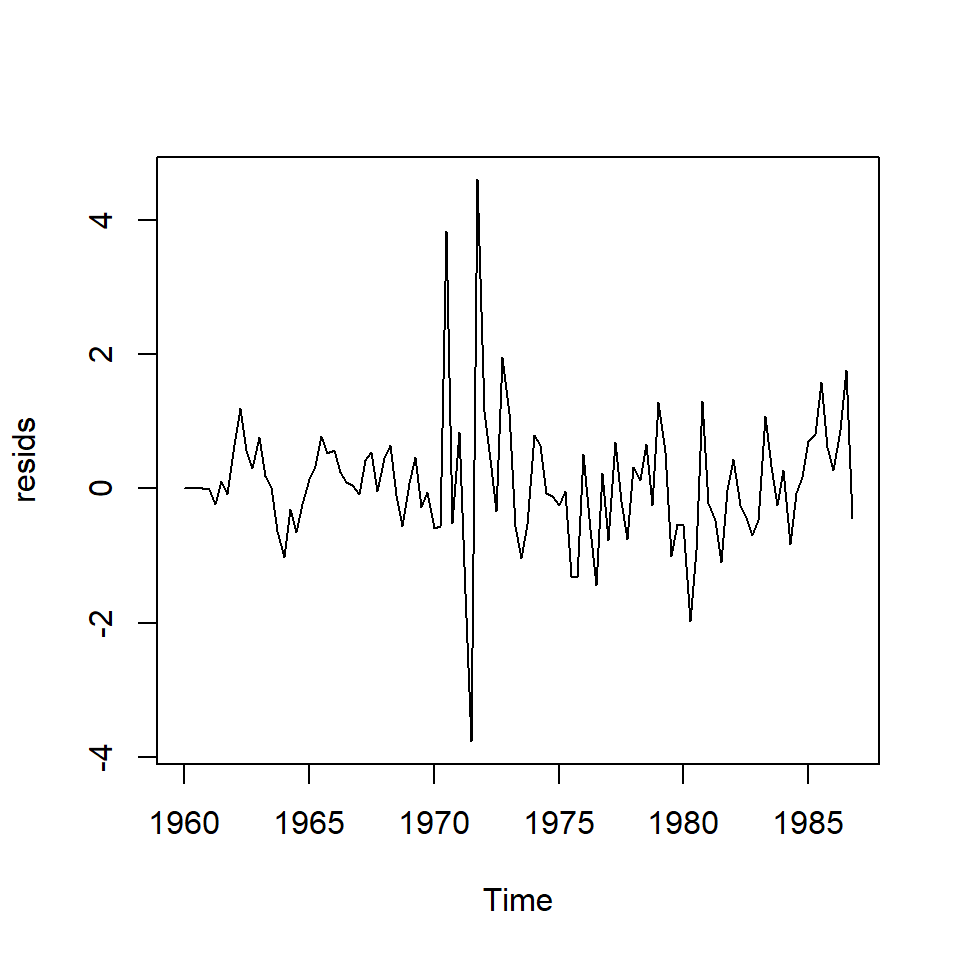
plot.ts(resids, ylab = "", xlab = "", col = "darkgrey", 
        lwd = 2)
abline(h = 0)
legend("topright", legend = "Residuales", lwd = 2, col = "darkgrey", 
       bty = "n")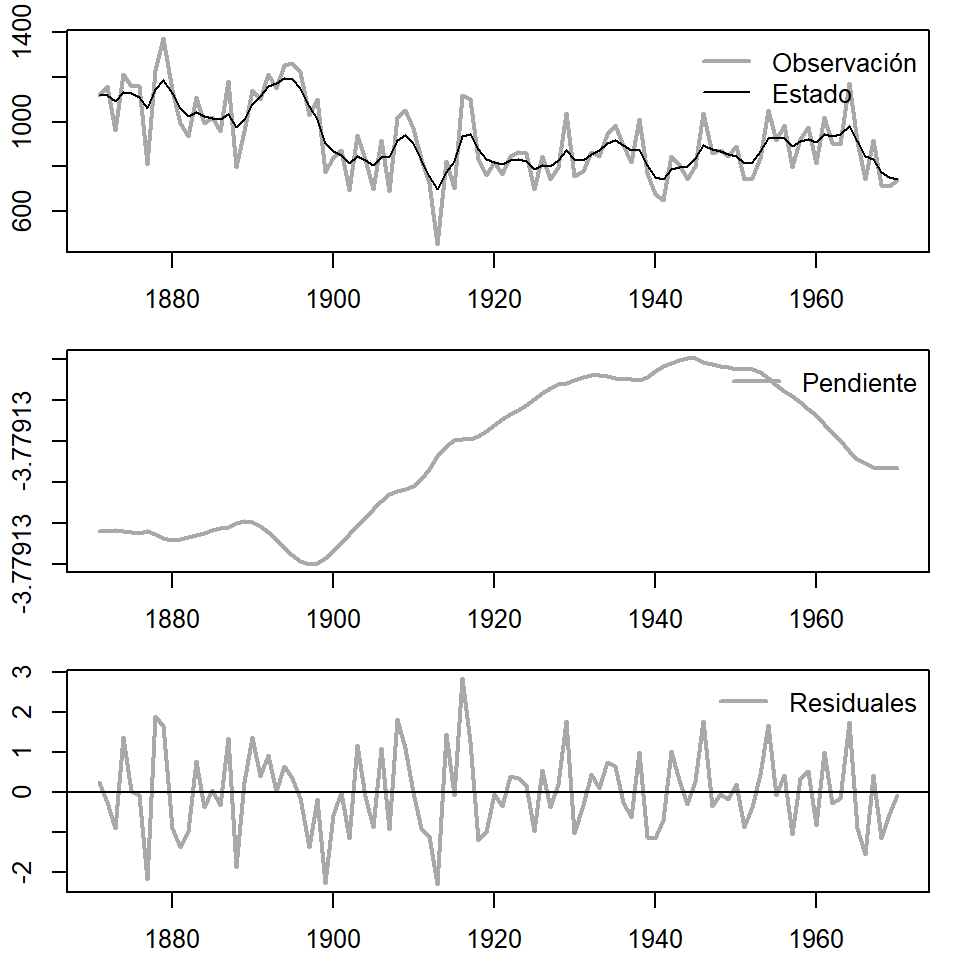

Ejemplo: AR(1)

Contenido

Introducción
El paquete dlm: funciones básicas
DLM de primer orden (Modelo de nivel local)
DLM de segundo orden
Ejemplo: AR(1)
Combinación de modelos de espacio de estados

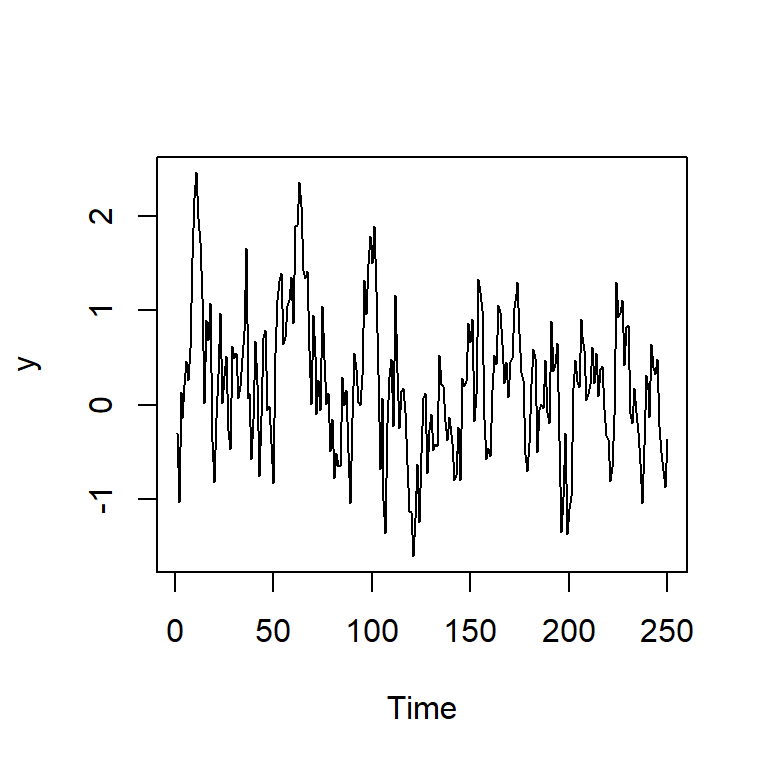
Ejemplo: AR(1)

Considere un AR(1): \[Y_t=\phi Y_{t-1}+a_t, \text{ para } t=1,2,...\]

set.seed(12345)
y = arima.sim(n=250,
              list(ar=0.75,ma=0),sd=0.5)
ts.plot(y)

Estimación usando Arima:

(mod.ar = Arima(y,order=c(1,0,0),
                include.mean=FALSE))

Series: y 
ARIMA(1,0,0) with zero mean 

Coefficients:
         ar1
      0.7384
s.e.  0.0422

sigma^2 = 0.2762:  log likelihood = -193.78
AIC=391.56   AICc=391.61   BIC=398.61

Habíamos visto su representación de espacio de estados:
- la ecuación de observaciones: \(~Y_t=\theta_t\)
- la ecuación de estados: \(~~~~~~~~~~\theta_t=\phi\theta_{t-1}+w_t,\)

donde \[\theta_1=Y_1=\sum_{j=0}^{\infty} \phi_1^j w_{1-j}\]

Del curso pasado, habíamos visto que:

\[E(\theta_t)=E(Y_t)=0 ~\text{, y}~~~\gamma_\theta(h)=\frac{\sigma_w^2 \phi^h}{1-\phi^2}\]

Para las condiciones iniciales, tenemos:
\[E(\theta_0)=0 ~\text{, y}~~~Var(\theta_0)=\gamma_\theta(0)=\frac{\sigma_w^2}{1-\phi^2}.\]
Es decir, \(F=1,, V=0, G=\phi, W=\sigma^2\)

dlm0 = function(parm){
  return(dlm(FF=1,V=0,GG=parm[1],W=parm[2]^2,
             m0=0,C0=solve(1-parm[1]^2)*parm[2]^2))
}

La estimación:

# Estimación
fitAR1 = dlmMLE(y=y,parm=c(0.7,1.0),build=dlm0,hessian=T)
# Estimaciones
(coef = fitAR1$par)

[1] 0.7383927 0.5244622

El error estándar:

var = solve(fitAR1$hessian)
sqrt(diag(var))

[1] 0.04223371 0.02345483

Pronóstico de 80% con dlmForecast:

mod = dlm0(fitAR1$par)
modf = dlmFilter(y,mod)

#pronóstico
pronostico = dlmForecast(modf,nAhead=5,method="plain")
hwidth <- qnorm(0.1, lower = FALSE)*sqrt(unlist(pronostico$Q))
fore <- cbind(pronostico$f, as.vector(pronostico$f) 
              + hwidth %o% c(-1, 1))
colnames(fore) <- c("forecast","li","ls")
fore

Time Series:
Start = 251 
End = 255 
Frequency = 1 
       forecast         li        ls
251 -0.26994808 -0.9420735 0.4021773
252 -0.19932769 -1.0348268 0.6361714
253 -0.14718212 -1.0595147 0.7651505
254 -0.10867820 -1.0602926 0.8429362
255 -0.08024719 -1.0526107 0.8921164

Pronóstico con Arima:

#Comparación con Arima
mod.ar = Arima(y,order=c(1,0,0),
               include.mean=FALSE)
forecast::forecast(mod.ar,h=5)

    Point Forecast      Lo 80     Hi 80     Lo 95     Hi 95
251    -0.26994825 -0.9434199 0.4035234 -1.299934 0.7600378
252    -0.19932795 -1.0365008 0.6378449 -1.479673 1.0810174
253    -0.14718240 -1.0613428 0.7669780 -1.545270 1.2509053
254    -0.10867848 -1.0621995 0.8448426 -1.566963 1.3496061
255    -0.08024745 -1.0545593 0.8940644 -1.570329 1.4098339

Combinación de modelos de espacio de estados

Contenido

Introducción
El paquete dlm: funciones básicas
DLM de primer orden (Modelo de nivel local)
DLM de segundo orden
Ejemplo: AR(1)
Combinación de modelos de espacio de estados

Combinación de modelos de espacio de estados

Suponga que tenemos \(i=1,...,k\) independientes DLMs para observaciones de \(m\) dimensiones.

\[\left. \begin{eqnarray} y_{t}^{(i)}&= & F_t^{(i)} \theta_{t}^{(i)} & + v_{t}^{(i)}, && v_{t}^{(i)}\sim N(0,V^{(i)})\\ \theta_{t}^{(i)}&= & G_t^{(i)} \theta_{t-1}^{(i)} & + w_{t}^{(i)},&& w_{t}^{(i)}\sim N(0,W^{(i)}) \end{eqnarray}\right.\]

para \(t=1,...,n,\) con las condiciones iniciales \(\theta_0^{(i)} \sim N_p(m_0^{(i)},C_0^{(i)})\) para \(i=1,...,k\).

Note que las dimensiones de los estados de cada DLM puede ser diferente. Denote \(p_1,...,p_k\) por las dimensiones de cada DLM.
Se puede especificar varios DLMs (tendencias, ARIMA, estacionalidad, variables exógenas, etc.) y sumarlas de forma independiente para formar un modelo que contempla todas estos componentes.

De esta forma, la observación en el tiempo \(t\) es el resultado de la suma de los modelos: \[y_t=y_t^{(1)}+...+y_t^{(k)}\] y las cantidades del modelo de espacio de estados sean definidas de la siguiente forma:

\[F_t=\left(F_t^{(1)} \mid ... \mid F_t^{(k)} \right),~~~ V_t=\sum_{i=1}^k V_t^{(i)}\] \[G_t=\begin{bmatrix} G_t^{(1)} & & \\ & \ddots & \\ & & G_t^{(k)} \end{bmatrix}~~W_t=\begin{bmatrix} W_t^{(1)} & & \\ & \ddots & \\ & & W_t^{(k)} \end{bmatrix}\] \[m'_t=\left({m_0^{(1)}}' ... {m_0^{(k)}}' \right),~~~ C_t=\begin{bmatrix} C_0^{(1)} & & \\ & \ddots & \\ & & C_0^{(k)} \end{bmatrix}\]

Ejemplo: `dlmModPoly` y `dlmModARMA`

n.obs = 250
yt = 2 + arima.sim(n=n.obs,list(ar=.75,ma=0),sd=.5)
plot(yt)

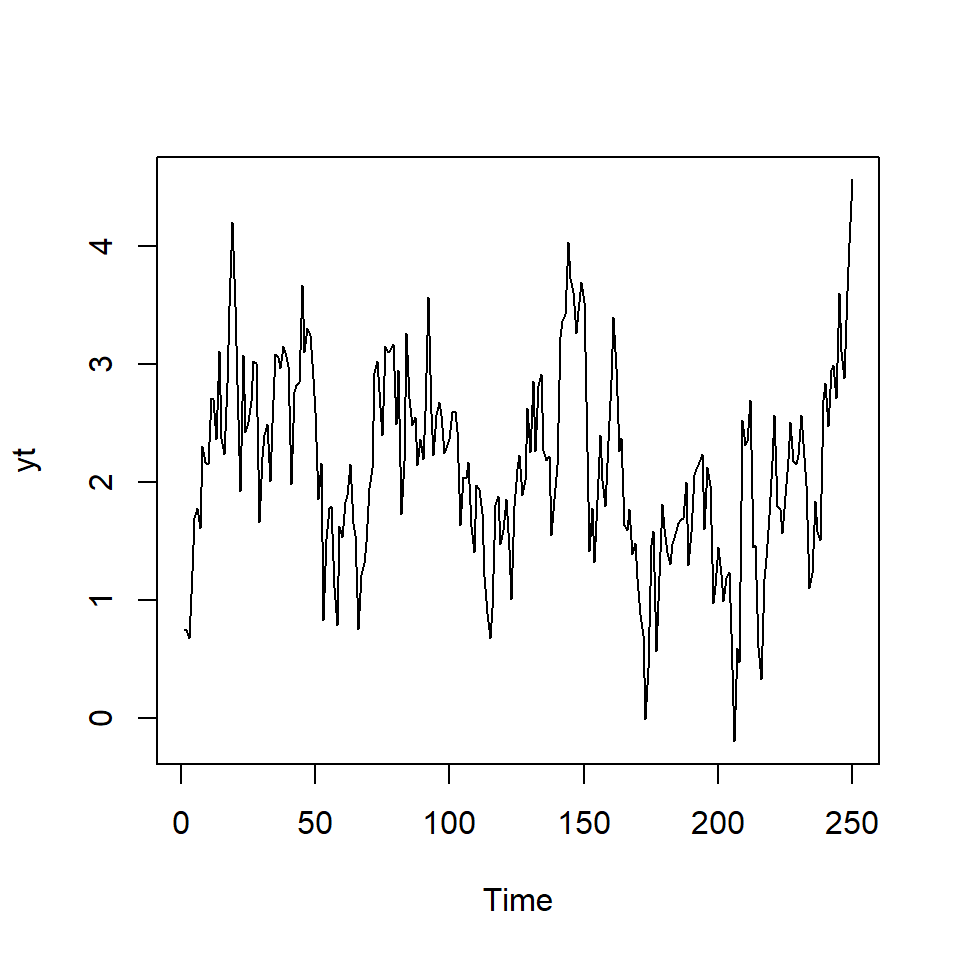
dlm1 = function(parm){
  dlm = dlmModPoly(1,dV=1e-7,dW=c(0)) +
    dlmModARMA(ar=parm[1], ma=NULL, sigma2=parm[2])
  # set initial state distribution
  dlm$C0[2,2] <- solve(1-parm[1]^2)*parm[2]
  return(dlm)
} 

# Estimación
fit1 = dlmMLE(y=yt,parm=c(0,0),build=dlm1,hessian=T)

Error in solve.default(1 - parm[1]^2): Lapack routine dgesv: system is exactly singular: U[1,1] = 0

Solución: restricción de parámetros (estimar el log de la variancia)

parm_rest = function(parm){
  return( c(parm[1],exp(parm[2])) )
}

# Configuración de DLM
dlm1 = function(parm){
  parm = parm_rest(parm)
  dlm = dlmModPoly(1,dV=1e-7,dW=c(0)) +
    dlmModARMA(ar=parm[1], ma=NULL, sigma2=parm[2])
  # set initial state distribution
  dlm$C0[2,2] <- solve(1-parm[1]^2)*parm[2]
  return(dlm)
} 

# Estimación
fit1 = dlmMLE(y=yt,parm=c(0,0),build=dlm1,hessian=T)

Los coeficientes estimados:

# estimación de la parte AR(1)
(coef = parm_rest(fit1$par))

[1] 0.8250812 0.2401968

# Error estándar
var = solve(fit1$hessian)
sqrt(diag(var))

[1] 0.03929948 0.08962646

La obtención de la media del proceso:

mod1 = dlm1(fit1$par)
mod1filt = dlmFilter(yt,mod1)

coef = mod1filt$m[n.obs+1]
covar = dlmSvd2var(mod1filt$U.C[[n.obs+1]],mod1filt$D.C[n.obs+1,])
coef.se = sqrt(covar[1,1])
coef; coef.se

[1] 2.147539

[1] 0.1739537

Factor estacional - dlmModSeas

Para un modelo estacional con periodo \(s\), podemos considerar estados de dimensión \((s-1)\):

\[F_t=(1,0,...,0),~~~ G=\begin{bmatrix} -1 & -1 & \dots & -1 & -1\\ 1 & 0 & \dots & 0 & 0\\ 0 & 1 & \dots & 0 & 0\\ \vdots & \vdots & \ddots & 0 & 0\\ 0 & 0 & \dots & 1 & 0 \end{bmatrix}\]

Variacia de las innovaciones de los estados: \(diag(W,...,0)\)

mod=dlmModSeas(frequency = 4, dV=3.5 ,dW=c(4.2,0,0))
mod$FF

     [,1] [,2] [,3]
[1,]    1    0    0

mod$V

     [,1]
[1,]  3.5

mod$GG

     [,1] [,2] [,3]
[1,]   -1   -1   -1
[2,]    1    0    0
[3,]    0    1    0

mod$W

     [,1] [,2] [,3]
[1,]  4.2    0    0
[2,]  0.0    0    0
[3,]  0.0    0    0

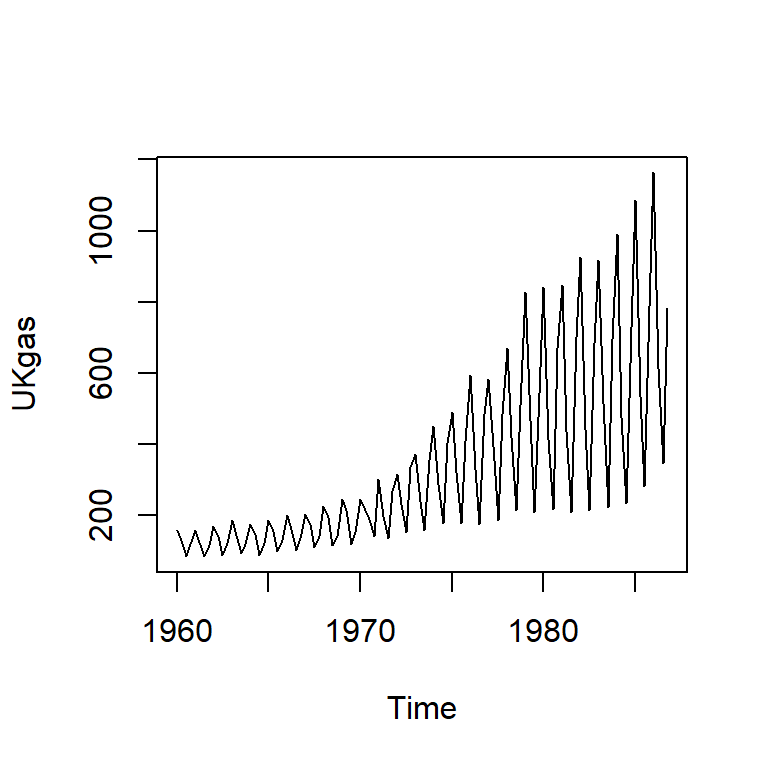
Ejemplo

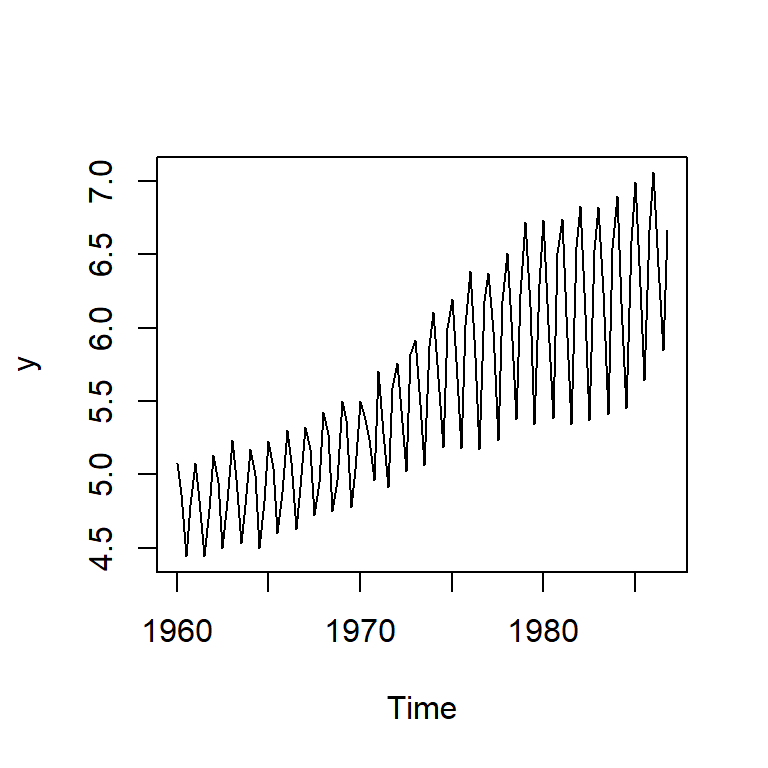
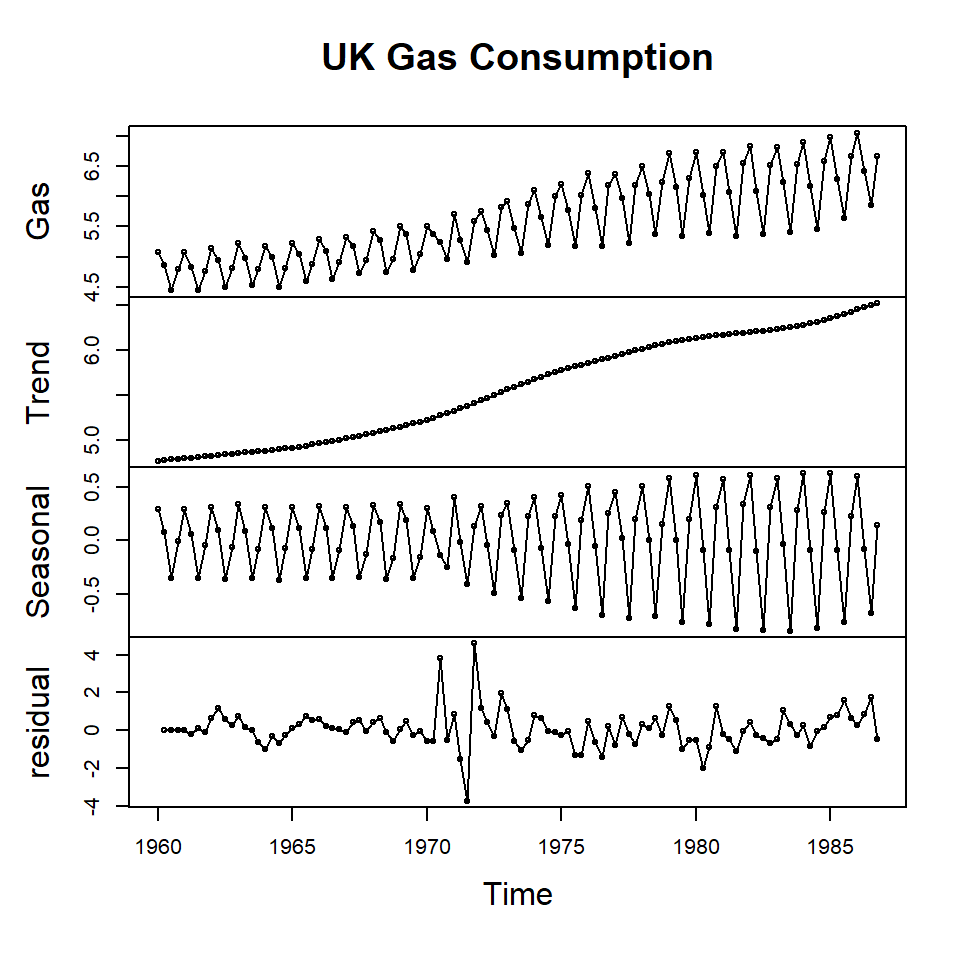
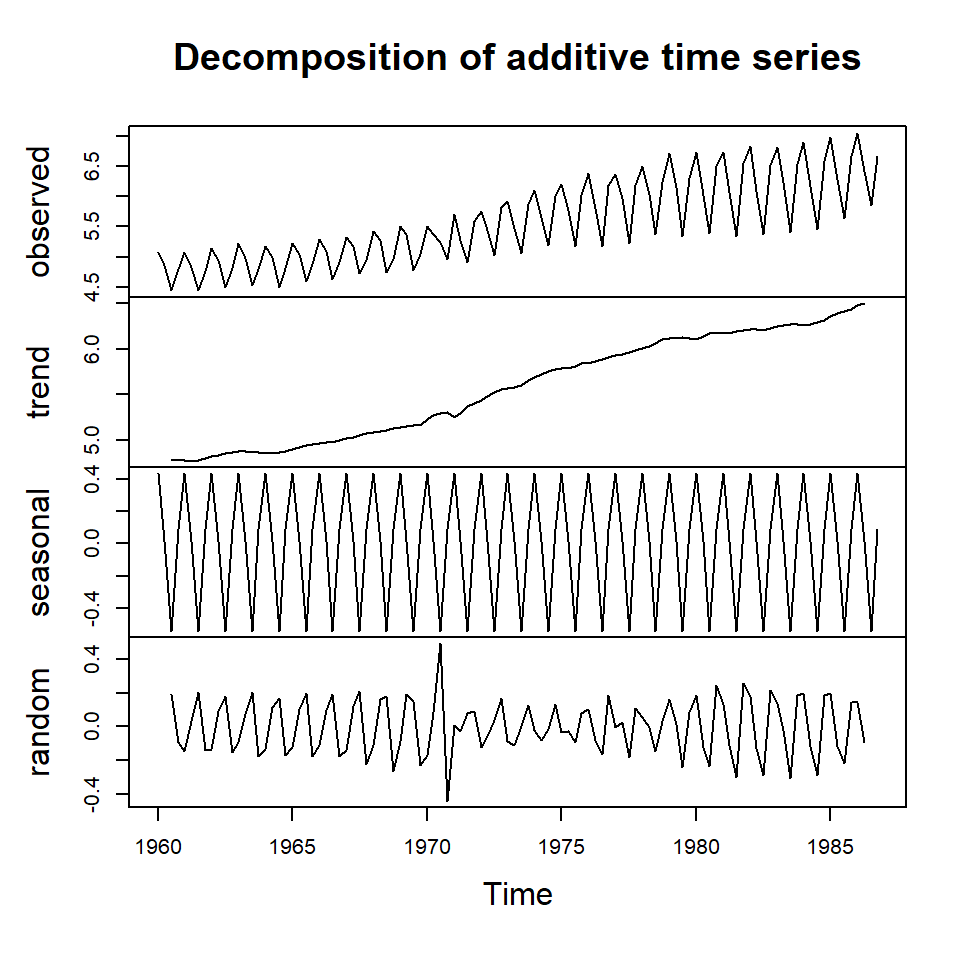
Consumo trimestral de gas en el Reino Unido desde el primer trimestre de 1960 hasta el cuarto trimestre de 1986, en millones de termas.

ts.plot(UKgas)

y = log(UKgas)
ts.plot(y)

Especificación y estimación de DLM:

dlm3 = dlmModPoly(2) + dlmModSeas(4)
dlm3_spec = function(x) {
  diag(W(dlm3))[2:3] = exp(x[1:2])
  V(dlm3) = exp(x[3])
  return(dlm3)
}

fit3 = dlmMLE(y,parm=c(0.1,0.1,0.1),build=dlm3_spec)
dlm3 = dlm3_spec(fit3$par)

Cálculo de los criterios de información:

loglik3 <- dlmLL(y, dlm3)
n.coef <- 3
r.aic3 <- (2 * (loglik3)) + 2 * (sum(n.coef))  #dlmLL caculates the neg. LL
r.bic3 <- (2 * (loglik3)) + (log(length(y))) * (n.coef)
r.aic3

[1] -270.2855

r.bic3

[1] -262.2391

ySmooth = dlmSmooth(y, mod = dlm3)
filteredgas <- dlmFilter(y, mod = dlm3)
resids <- residuals(filteredgas, sd = FALSE)
plot(resids)

x = cbind(y, dropFirst(ySmooth$s[, c(1, 3)]),dropFirst(resids))
colnames(x) = c("Gas", "Trend", "Seasonal","residual")
plot(x, type = "o", main = "UK Gas Consumption")

descomposicion=decompose(y)
plot(descomposicion)

Tema 3: Modelos de Espacio-Estado(2)

Introducción

Introducción

El paquete dlm: funciones básicas

El paquete dlm: funciones básicas

DLM de primer orden (Modelo de nivel local)

DLM de primer orden (Modelo de nivel local)

Ejemplo: Caudal anual del Rio Nilo

DLM de segundo orden

DLM de segundo orden

Ejemplo: Caudal anual del Rio Nilo

Ejemplo: AR(1)

Ejemplo: AR(1)

Combinación de modelos de espacio de estados

Combinación de modelos de espacio de estados

Ejemplo: dlmModPoly y dlmModARMA

Factor estacional - dlmModSeas

Ejemplo

Tema 3: Modelos de Espacio-Estado⁽²⁾

El paquete `dlm`: funciones básicas

El paquete `dlm`: funciones básicas

Ejemplo: `dlmModPoly` y `dlmModARMA`