Tema 4: Modelos no lineales. ARCH, GARCH y extensiones

Curso: Tópicos Avanzados de Series Temporales

Autor/a

Afiliación

Escuela de Estadística, Universidad de Costa Rica

1 librerías

library(fGarch)
library(rugarch)
library(astsa)
library(forecast)
library(quantmod)

2 Ejemplo: promedio diario industrial Dow Jone

getSymbols("^DJI",from = "2016/12/31",
           to = "2018/12/31",
           periodicity = "daily")

[1] "DJI"

y <- DJI$DJI.Close

2.1 Retornos

r <- diff(log(y))[-1]
colnames(r)<-"r"

ts.plot(y)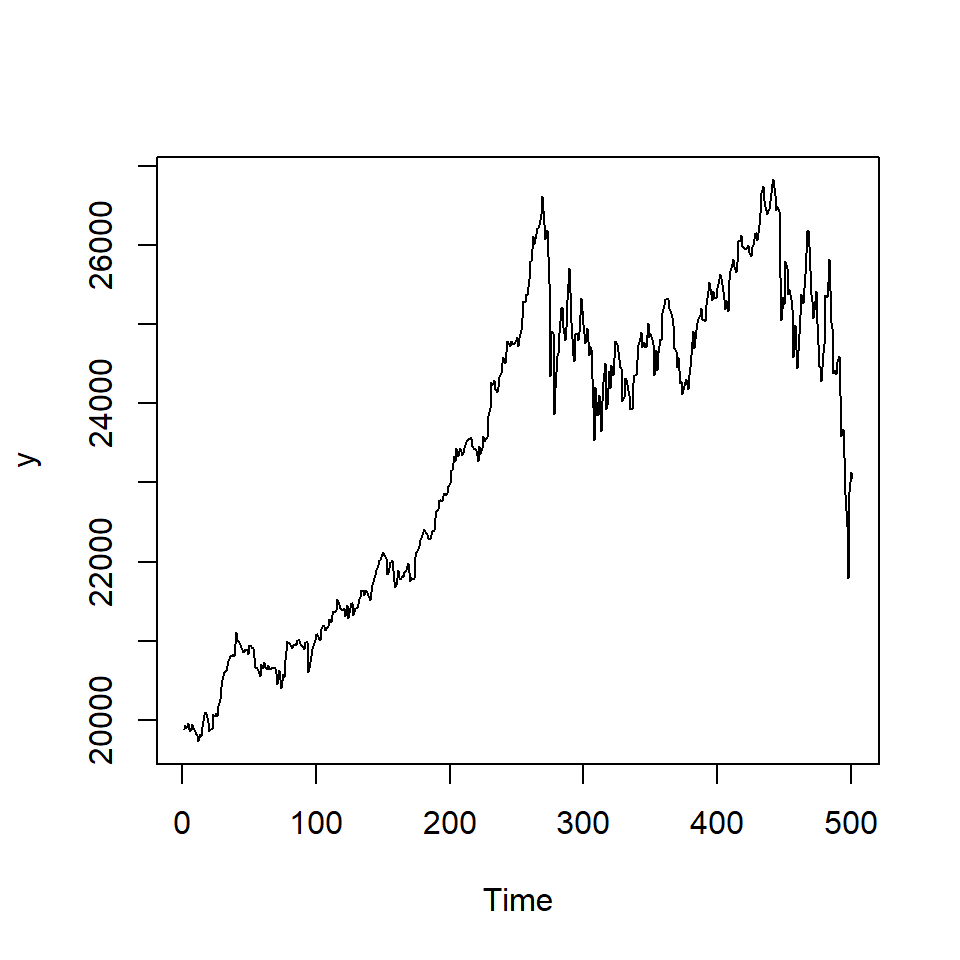

ts.plot(r)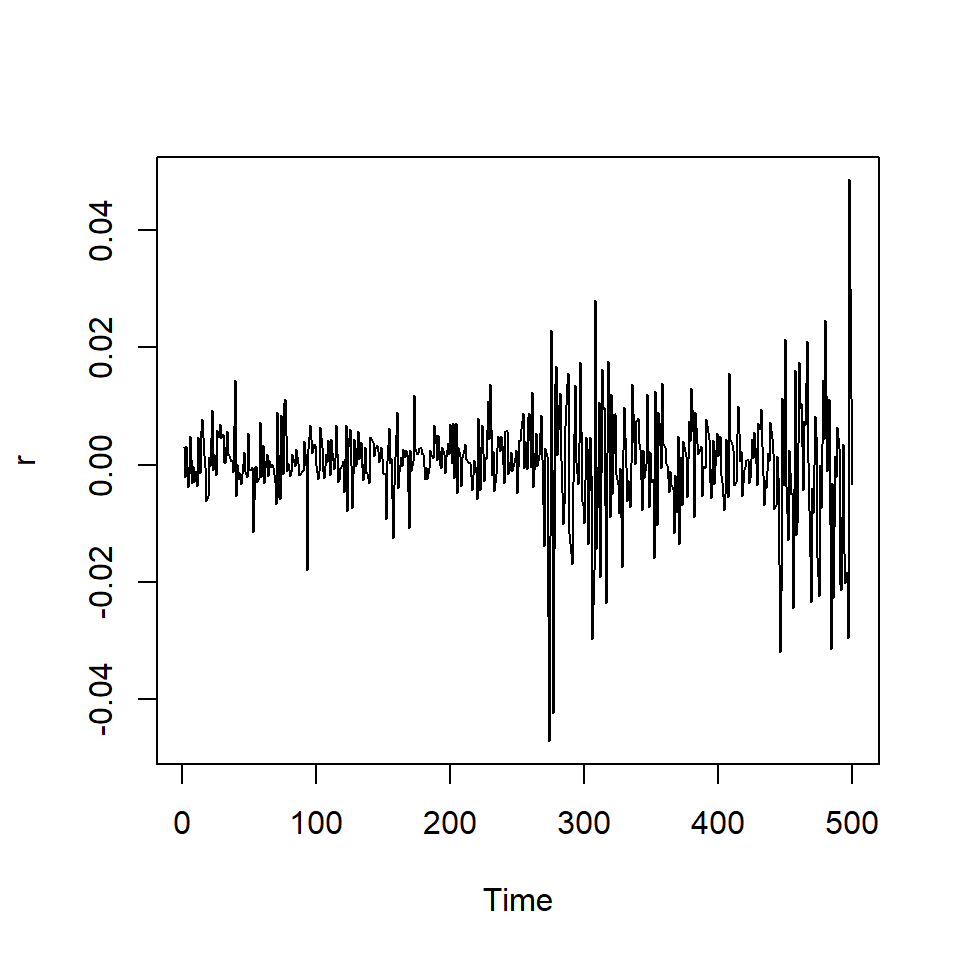

acf2(y)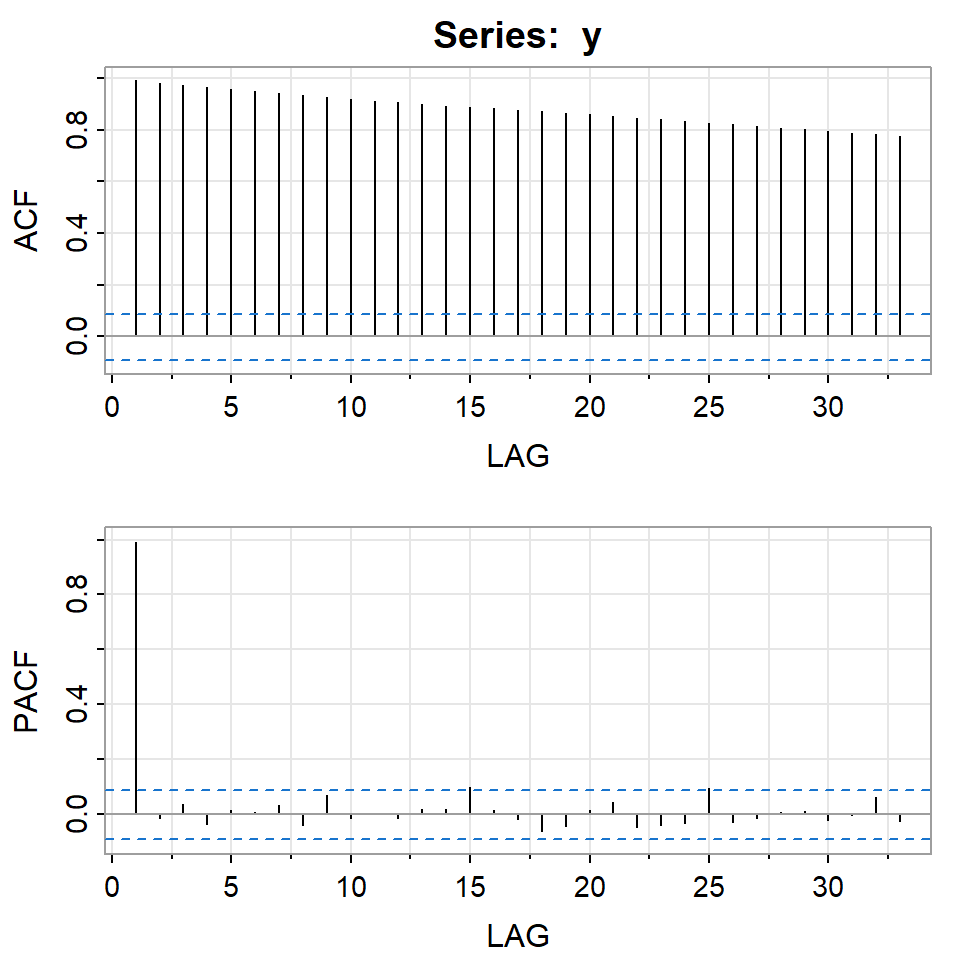

     [,1]  [,2] [,3]  [,4] [,5] [,6] [,7]  [,8] [,9] [,10] [,11] [,12] [,13]
ACF  0.99  0.98 0.97  0.97 0.96 0.95 0.94  0.93 0.93  0.92  0.91  0.91  0.90
PACF 0.99 -0.02 0.04 -0.04 0.01 0.01 0.03 -0.04 0.07 -0.02  0.00 -0.02  0.02
     [,14] [,15] [,16] [,17] [,18] [,19] [,20] [,21] [,22] [,23] [,24] [,25]
ACF   0.89  0.89  0.88  0.88  0.87  0.87  0.86  0.85  0.85  0.84  0.83  0.83
PACF  0.02  0.10  0.02 -0.02 -0.06 -0.04  0.01  0.04 -0.05 -0.04 -0.03  0.09
     [,26] [,27] [,28] [,29] [,30] [,31] [,32] [,33]
ACF   0.82  0.81  0.81  0.80  0.79  0.79  0.78  0.78
PACF -0.03 -0.02  0.01  0.01 -0.02 -0.01  0.06 -0.02

acf2(r)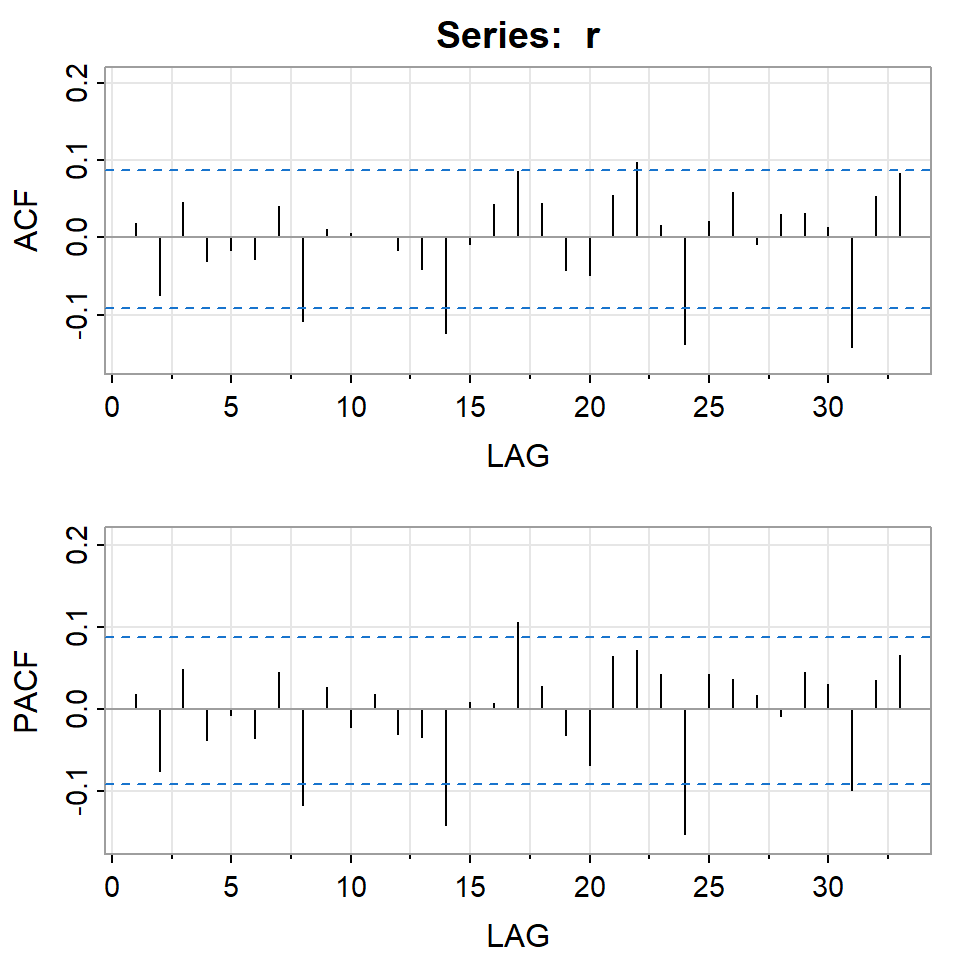

     [,1]  [,2] [,3]  [,4]  [,5]  [,6] [,7]  [,8] [,9] [,10] [,11] [,12] [,13]
ACF  0.02 -0.07 0.05 -0.03 -0.02 -0.03 0.04 -0.11 0.01  0.01  0.00 -0.02 -0.04
PACF 0.02 -0.08 0.05 -0.04 -0.01 -0.04 0.04 -0.12 0.03 -0.02  0.02 -0.03 -0.03
     [,14] [,15] [,16] [,17] [,18] [,19] [,20] [,21] [,22] [,23] [,24] [,25]
ACF  -0.12 -0.01  0.04  0.09  0.05 -0.04 -0.05  0.05  0.10  0.02 -0.14  0.02
PACF -0.14  0.01  0.01  0.11  0.03 -0.03 -0.07  0.06  0.07  0.04 -0.15  0.04
     [,26] [,27] [,28] [,29] [,30] [,31] [,32] [,33]
ACF   0.06 -0.01  0.03  0.03  0.01 -0.14  0.05  0.08
PACF  0.04  0.02 -0.01  0.04  0.03 -0.10  0.04  0.07

Los retornos tienen colas pesadas y son asimétricos.

hist(r,breaks=25,freq=FALSE)
curve(dnorm(x,mean(r,na.rm = T),sd(r,na.rm = TRUE)),add=T,col=2)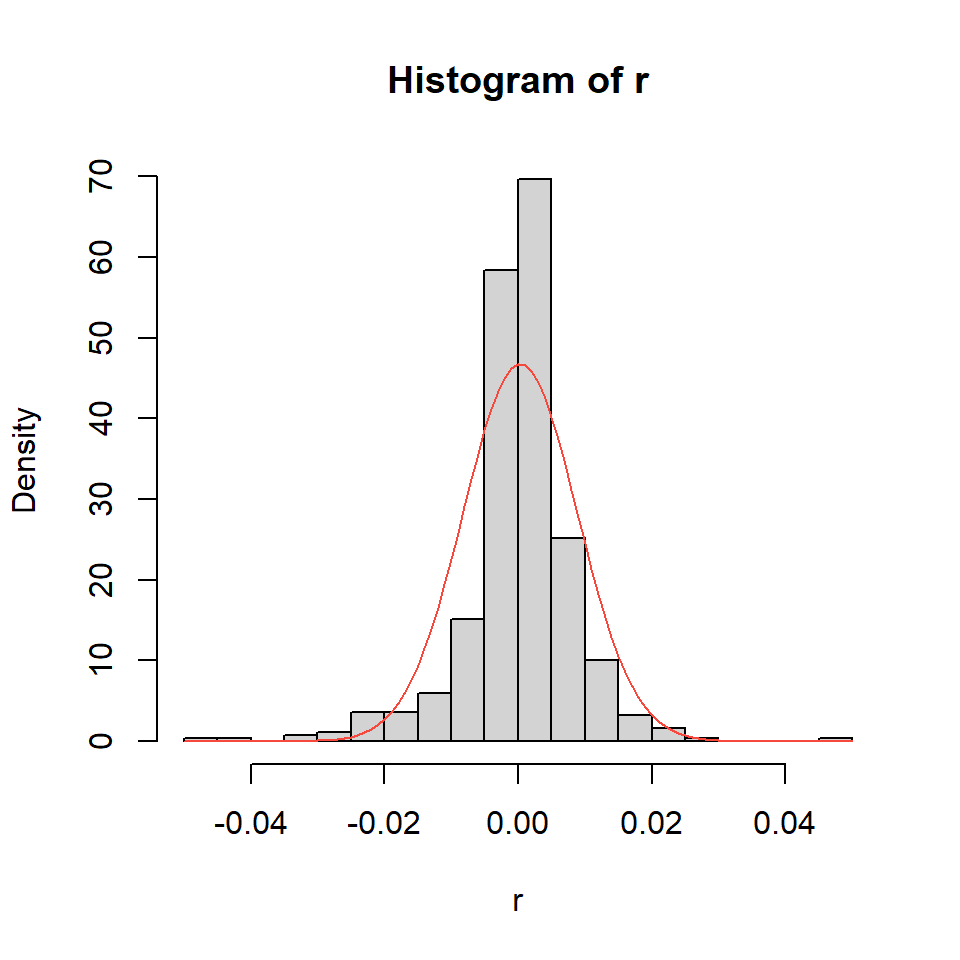

2.2 `auto.arima`

Empezamos con un modelo ARMA.

auto_arima <- auto.arima(r)
summary(auto_arima)

Series: r 
ARIMA(1,0,1) with zero mean 

Coefficients:
          ar1     ma1
      -0.8620  0.9465
s.e.   0.0412  0.0250

sigma^2 = 7.115e-05:  log likelihood = 1679.09
AIC=-3352.18   AICc=-3352.14   BIC=-3339.54

Training set error measures:
                       ME        RMSE         MAE      MPE     MAPE      MASE
Training set 0.0002870584 0.008418193 0.005530544 97.79074 159.9398 0.7157715
                    ACF1
Training set -0.03871362

checkresiduals(auto_arima)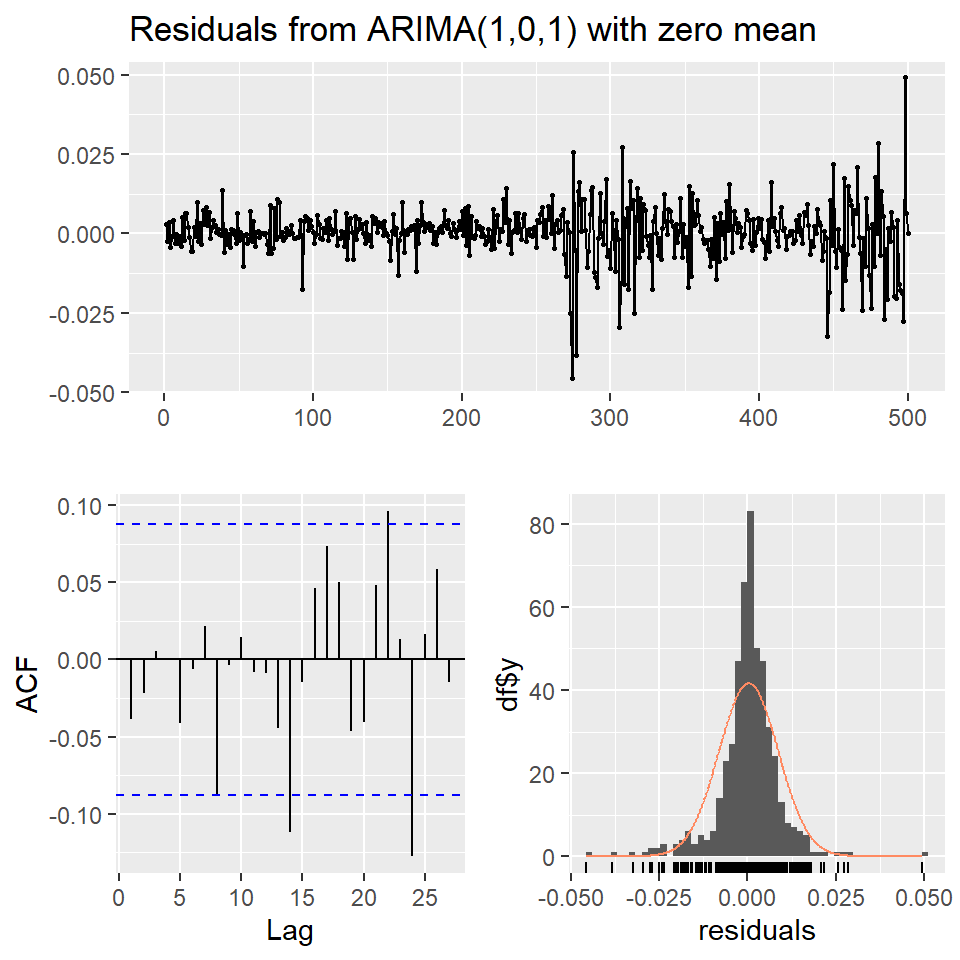


    Ljung-Box test

data:  Residuals from ARIMA(1,0,1) with zero mean
Q* = 6.1604, df = 8, p-value = 0.6293

Model df: 2.   Total lags used: 10

residuals<-auto_arima$res
acf2(residuals)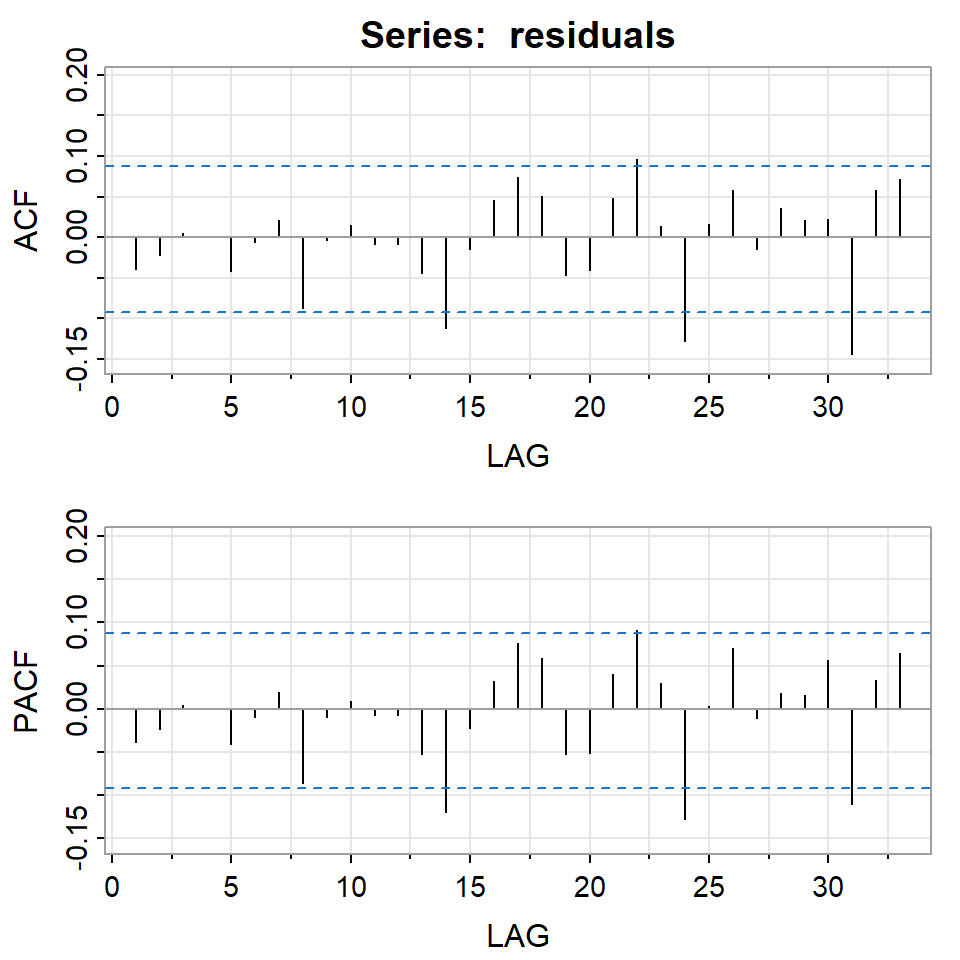

      [,1]  [,2] [,3] [,4]  [,5]  [,6] [,7]  [,8]  [,9] [,10] [,11] [,12] [,13]
ACF  -0.04 -0.02 0.01    0 -0.04 -0.01 0.02 -0.09  0.00  0.01 -0.01 -0.01 -0.04
PACF -0.04 -0.02 0.00    0 -0.04 -0.01 0.02 -0.09 -0.01  0.01 -0.01 -0.01 -0.05
     [,14] [,15] [,16] [,17] [,18] [,19] [,20] [,21] [,22] [,23] [,24] [,25]
ACF  -0.11 -0.01  0.05  0.07  0.05 -0.05 -0.04  0.05  0.10  0.01 -0.13  0.02
PACF -0.12 -0.02  0.03  0.08  0.06 -0.05 -0.05  0.04  0.09  0.03 -0.13  0.00
     [,26] [,27] [,28] [,29] [,30] [,31] [,32] [,33]
ACF   0.06 -0.01  0.04  0.02  0.02 -0.14  0.06  0.07
PACF  0.07 -0.01  0.02  0.02  0.06 -0.11  0.03  0.06

acf2(residuals^2)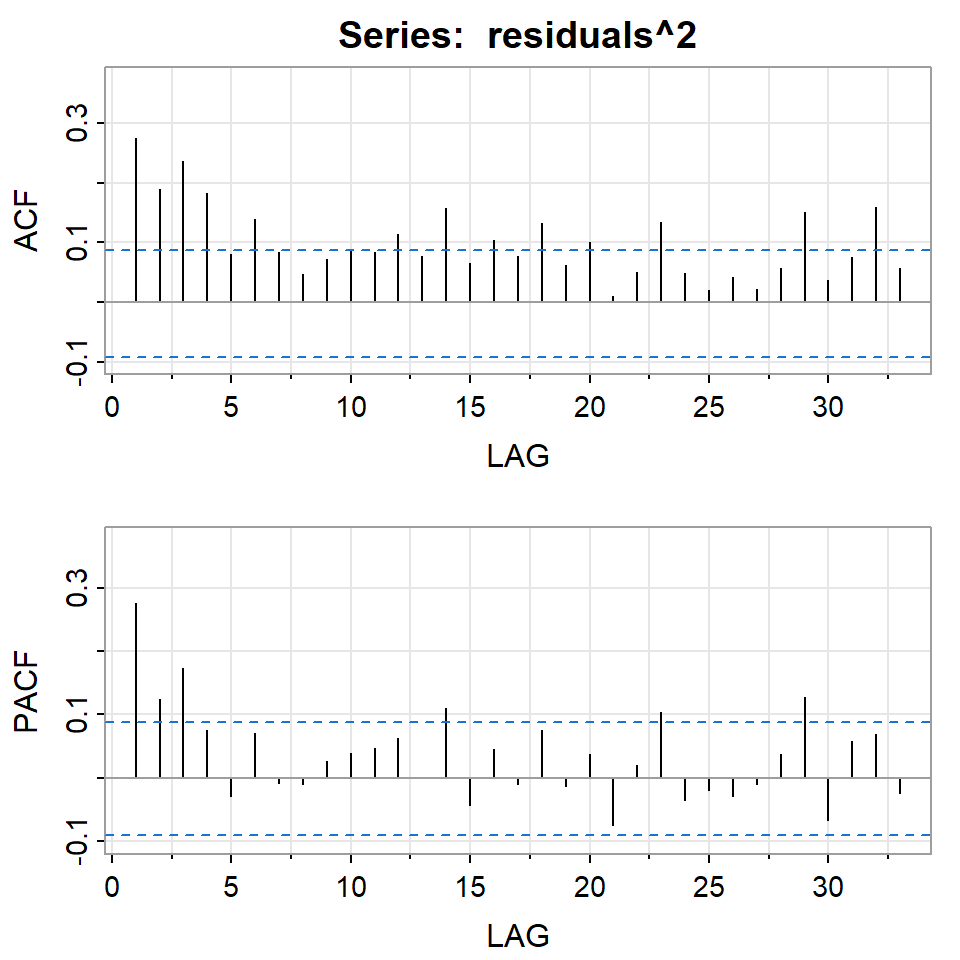

     [,1] [,2] [,3] [,4]  [,5] [,6]  [,7]  [,8] [,9] [,10] [,11] [,12] [,13]
ACF  0.28 0.19 0.24 0.18  0.08 0.14  0.08  0.05 0.07  0.09  0.08  0.11  0.08
PACF 0.28 0.12 0.17 0.08 -0.03 0.07 -0.01 -0.01 0.03  0.04  0.05  0.06  0.00
     [,14] [,15] [,16] [,17] [,18] [,19] [,20] [,21] [,22] [,23] [,24] [,25]
ACF   0.16  0.07  0.10  0.08  0.13  0.06  0.10  0.01  0.05  0.13  0.05  0.02
PACF  0.11 -0.04  0.04 -0.01  0.08 -0.01  0.04 -0.08  0.02  0.10 -0.04 -0.02
     [,26] [,27] [,28] [,29] [,30] [,31] [,32] [,33]
ACF   0.04  0.02  0.06  0.15  0.04  0.08  0.16  0.06
PACF -0.03 -0.01  0.04  0.13 -0.07  0.06  0.07 -0.03

Hay autocorrelación de los residuales al cuadrado.
Indicación de que hay variabilidad condicional.

2.3 ARMA(1,1)+ARCH(1)

arma.arch1 <- garchFit(r~arma(1,1)+garch(1,0), data=r,trace=F)
round(arma.arch1@fit$matcoef, 4)

        Estimate  Std. Error  t value Pr(>|t|)
mu        0.0008      0.0006   1.2336   0.2173
ar1      -0.8282      0.0505 -16.3953   0.0000
ma1       0.9204      0.0365  25.2337   0.0000
omega     0.0000      0.0000  11.8647   0.0000
alpha1    0.3820      0.0874   4.3736   0.0000

plot(arma.arch1,which=10)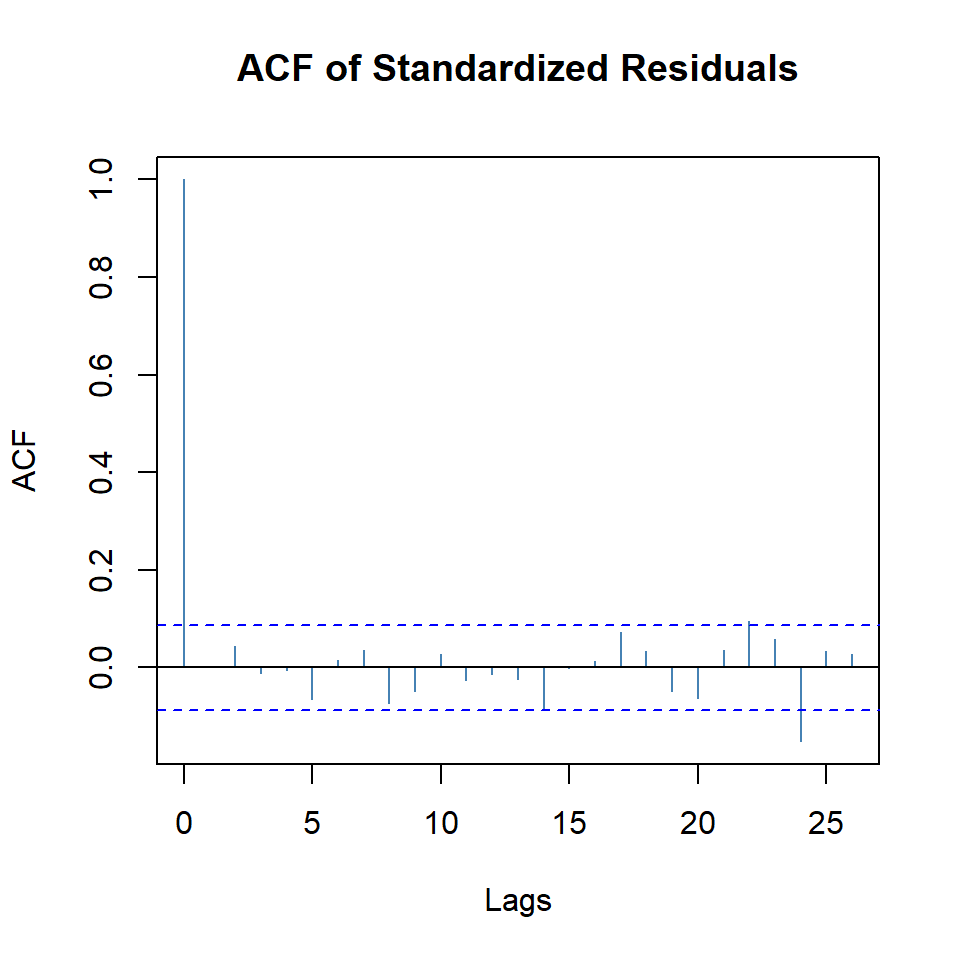

plot(arma.arch1,which=11)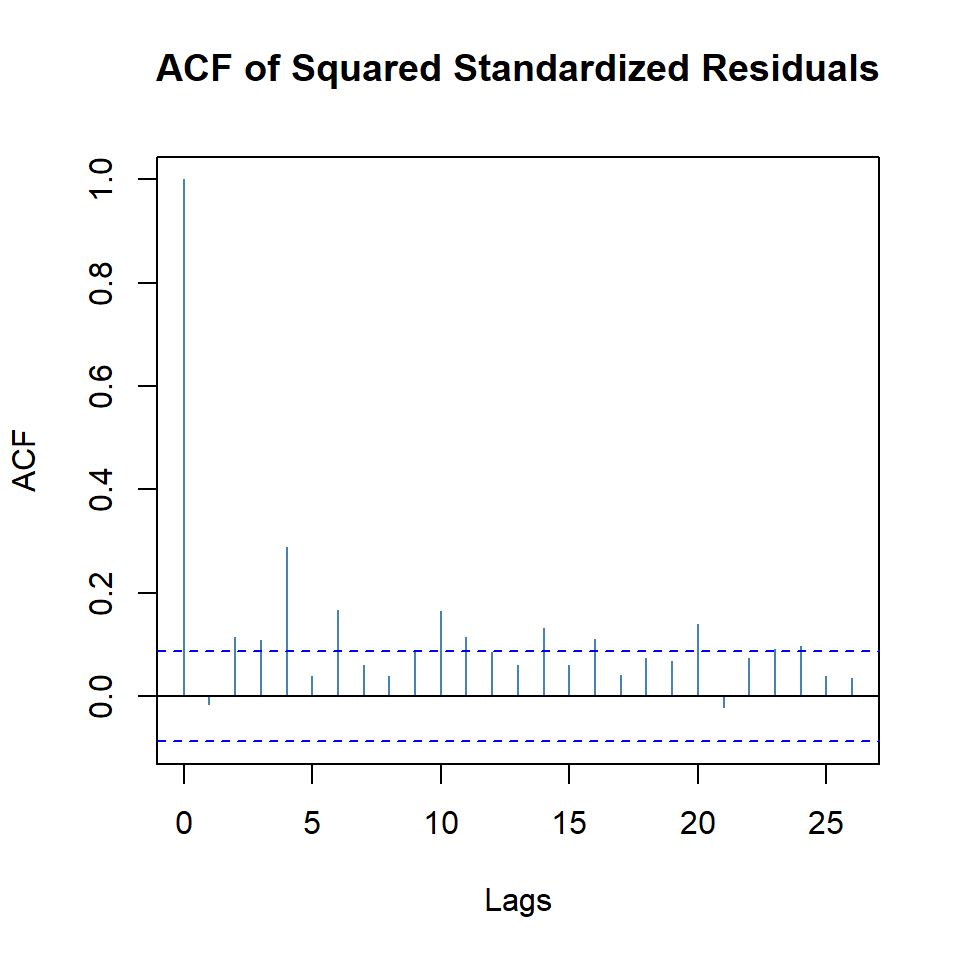

Note que todavía existe autocorrelación de los residuales al cuadrado.

2.4 ARMA(1,1)+GARCH(1,1)

arma.garch11 <- garchFit(r~arma(1,1)+garch(1,1), data=r,trace=F)
round(arma.garch11@fit$matcoef, 4)

        Estimate  Std. Error  t value Pr(>|t|)
mu        0.0015      0.0007   2.2800   0.0226
ar1      -0.5869      0.5305  -1.1062   0.2686
ma1       0.5889      0.5449   1.0808   0.2798
omega     0.0000      0.0000   2.2750   0.0229
alpha1    0.1598      0.0400   3.9919   0.0001
beta1     0.8281      0.0431  19.2312   0.0000

plot(arma.garch11,which=10)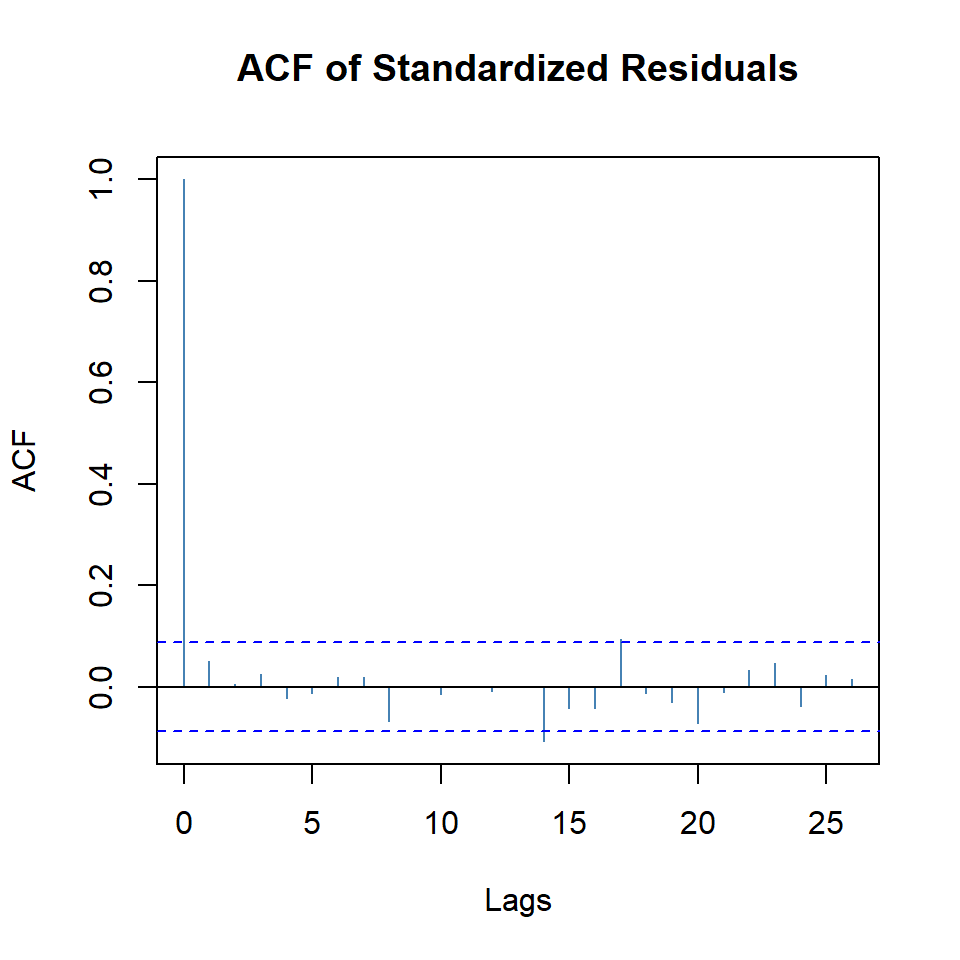

plot(arma.garch11,which=11)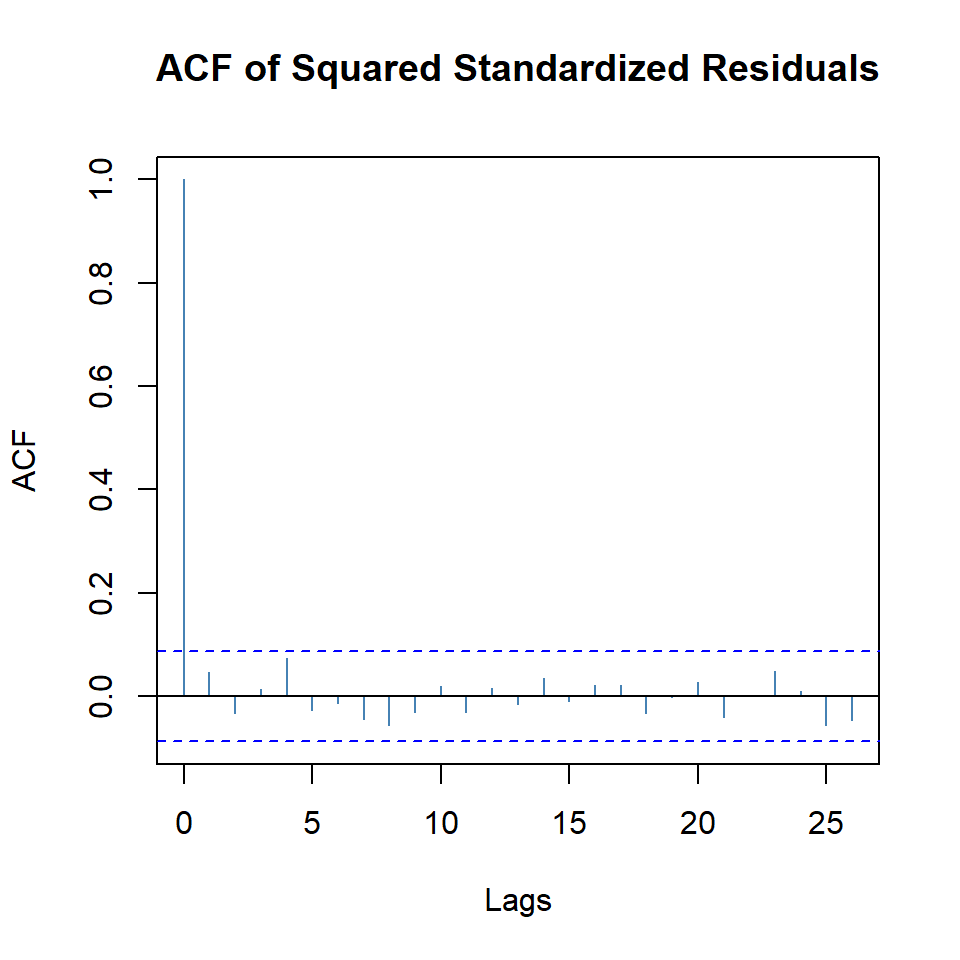

:::

plot(arma.garch11,which=13)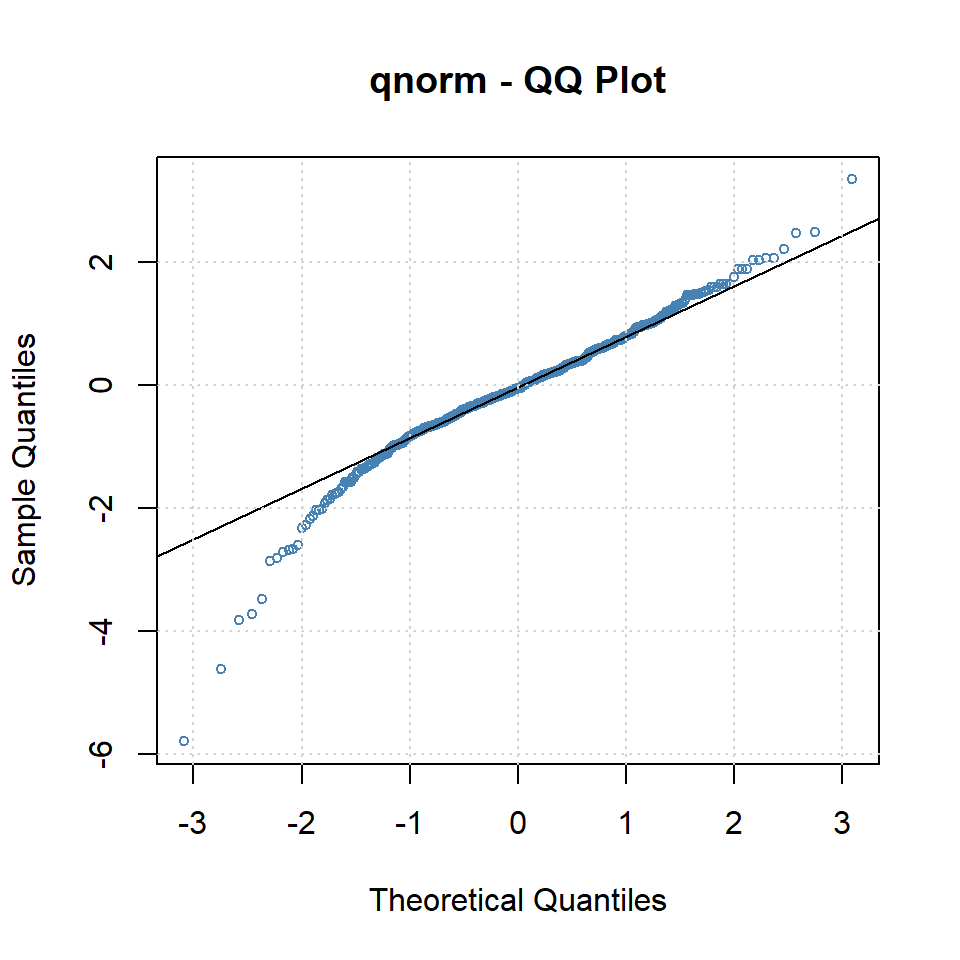

Note que no existe autocorrelación de los residuales al cuadrado, pero los residuales no son normales.
El modelo está bien, pero hay coeficientes no significativos.
Procedemos a eliminarlos.

2.5 GARCH(1,1)

garch11 <- garchFit(r~garch(1,1), data=r,trace=F)
round(garch11@fit$matcoef, 4)

        Estimate  Std. Error  t value Pr(>|t|)
mu        0.0010      0.0003   3.6563   0.0003
omega     0.0000      0.0000   2.2971   0.0216
alpha1    0.1594      0.0397   4.0151   0.0001
beta1     0.8285      0.0426  19.4699   0.0000

Comparando los criterios de información, el modelo reducido es mejor.

garch11@fit$ics

      AIC       BIC       SIC      HQIC 
-7.151073 -7.117356 -7.151200 -7.137843

arma.garch11@fit$ics

      AIC       BIC       SIC      HQIC 
-7.143874 -7.093298 -7.144157 -7.124028

plot(garch11, which = 10)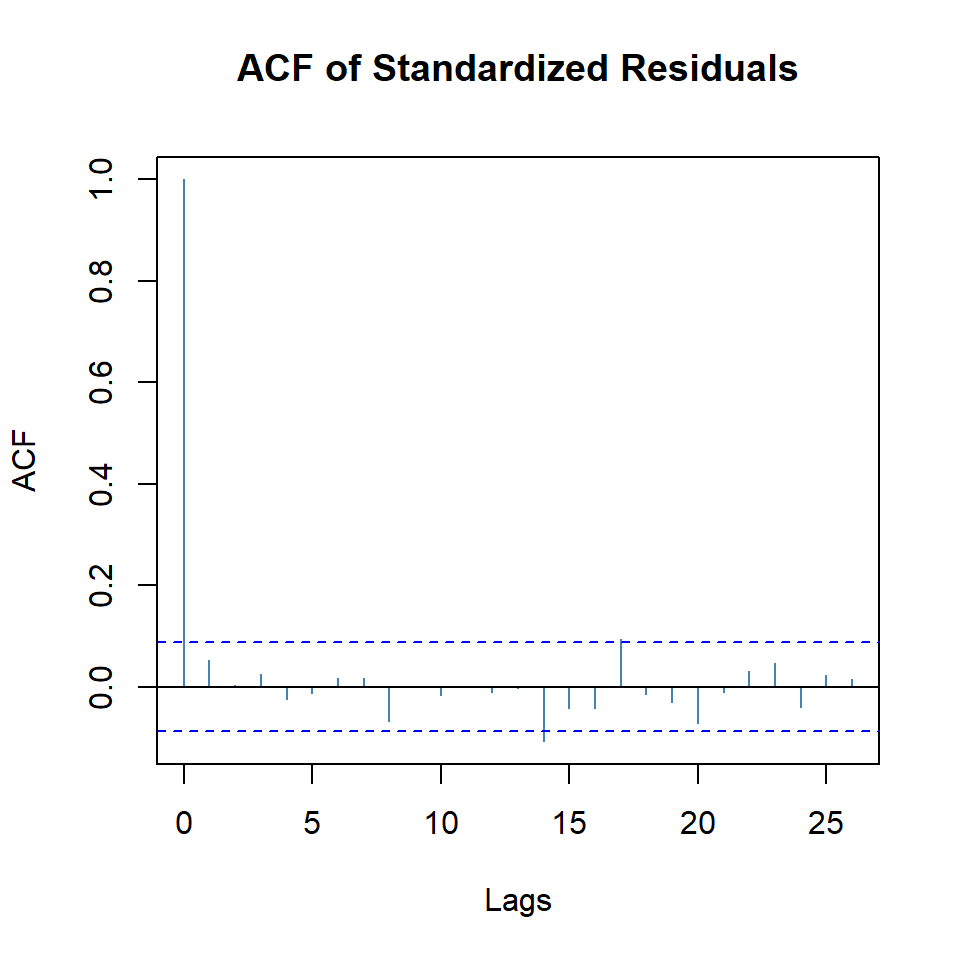

plot(garch11, which = 11)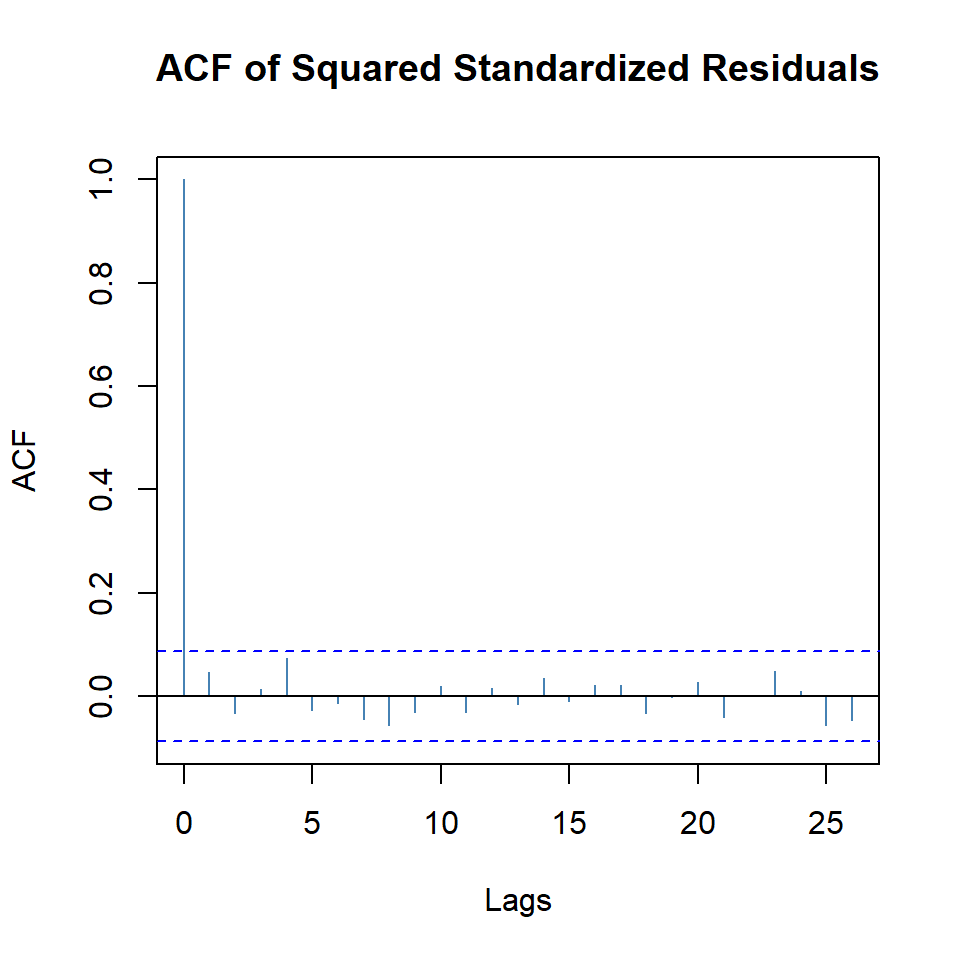

plot(arma.garch11,which=13)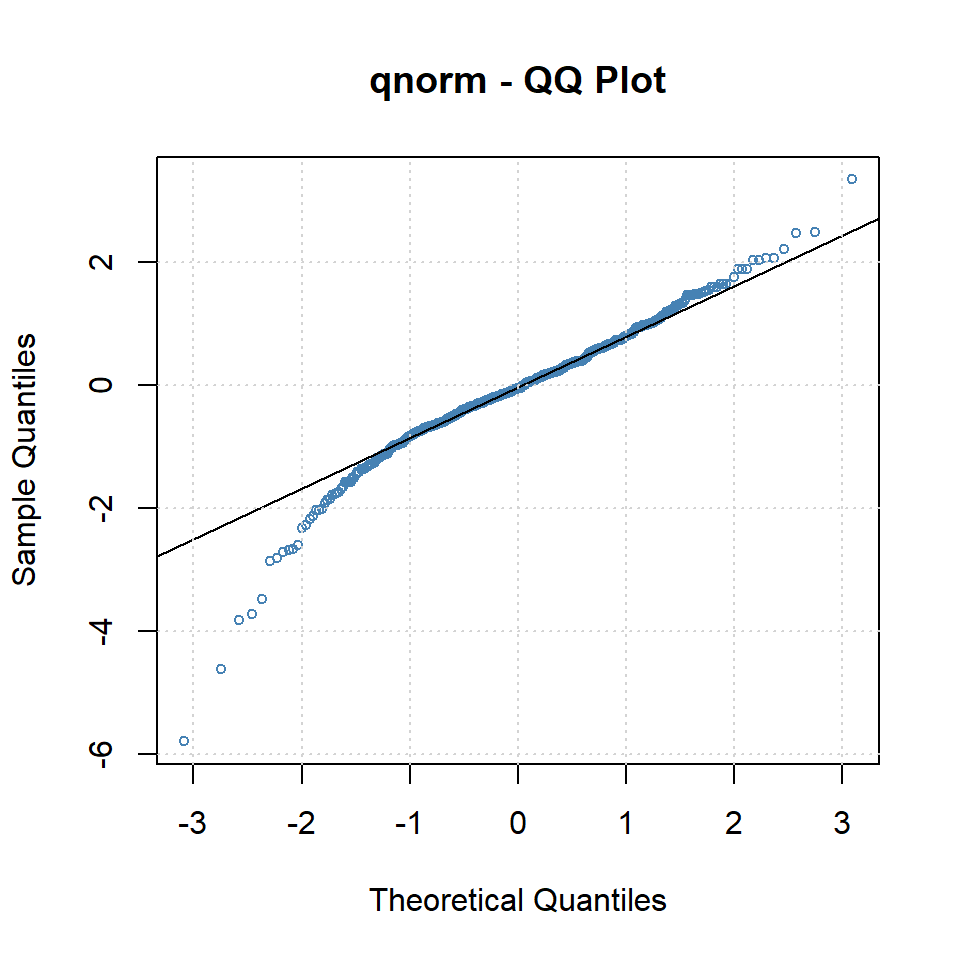

El modelo GARCH(1,1) va ganando, pero la normalidad no se cumple.

2.6 T-GARCH

Empezamos con TGARCH con valor absoluto, delta=1.

tgarch11.1 = garchFit(r~garch(1,1),delta=1,leverage=T,data=r,trace=F,include.mean=F)
arma.tgarch11.1 = garchFit(r~arma(1,1)+garch(1,1),delta=1,leverage=T,data=r,trace=F,include.mean=F)

Empezamos con TGARCH con cuadrado, delta=2.

tgarch11.2 = garchFit(r~garch(1,1),delta=2,leverage=T,data=r,trace=F,include.mean=F)
arma.tgarch11.2 = garchFit(r~arma(1,1)+garch(1,1),delta=2,leverage=T,data=r,trace=F,include.mean=F)

garch11@fit$ics

      AIC       BIC       SIC      HQIC 
-7.151073 -7.117356 -7.151200 -7.137843

tgarch11.1@fit$ics

      AIC       BIC       SIC      HQIC 
-7.123718 -7.090002 -7.123845 -7.110488

arma.tgarch11.1@fit$ics

      AIC       BIC       SIC      HQIC 
-7.199735 -7.149160 -7.200019 -7.179890

tgarch11.2@fit$ics

      AIC       BIC       SIC      HQIC 
-7.173335 -7.139618 -7.173461 -7.160104

arma.tgarch11.2@fit$ics

      AIC       BIC       SIC      HQIC 
-7.166148 -7.115572 -7.166431 -7.146302

El modelo ganador es arma.tgarch11.1

round(arma.tgarch11.1@fit$matcoef, 4)

        Estimate  Std. Error  t value Pr(>|t|)
ar1      -0.8429      0.0667 -12.6414        0
ma1       0.8996      0.0596  15.0830        0
omega     0.0005      0.0001   4.4732        0
alpha1    0.1494      0.0292   5.1203        0
gamma1    0.7858      0.1627   4.8302        0
beta1     0.8284      0.0297  27.9142        0

plot(arma.tgarch11.1, which = 10)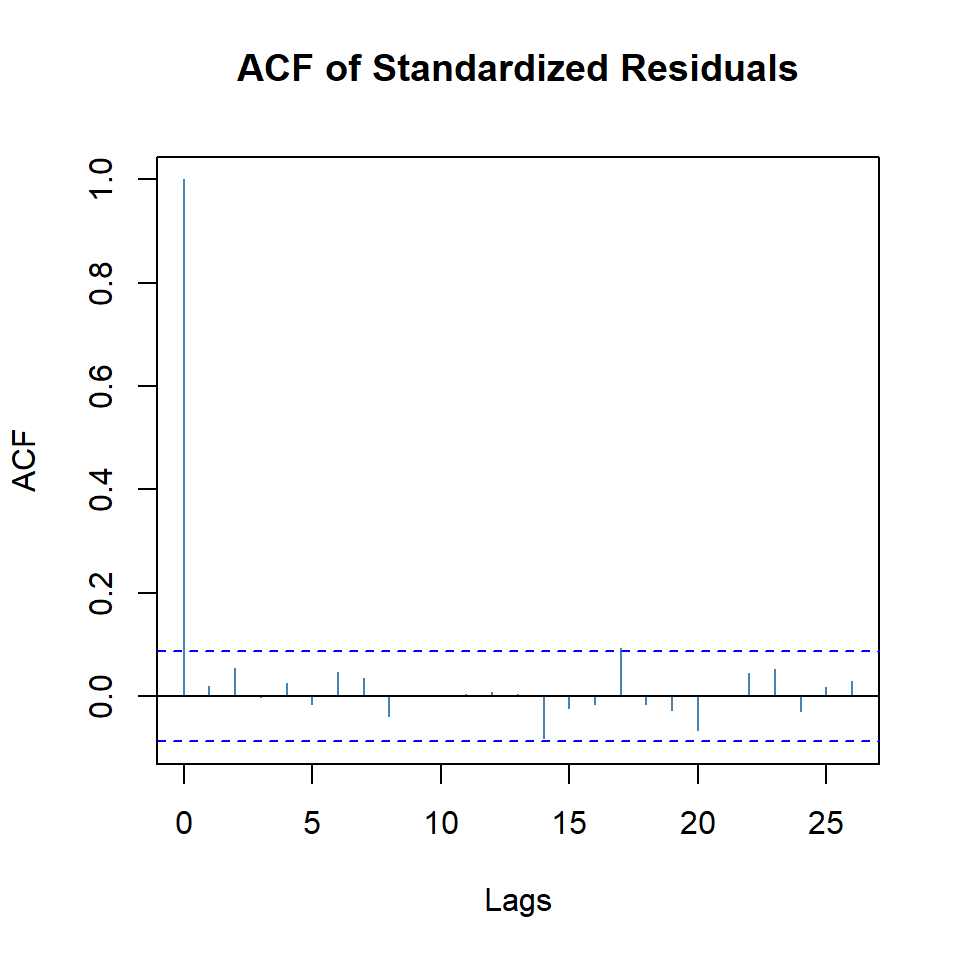

plot(arma.tgarch11.1, which = 11)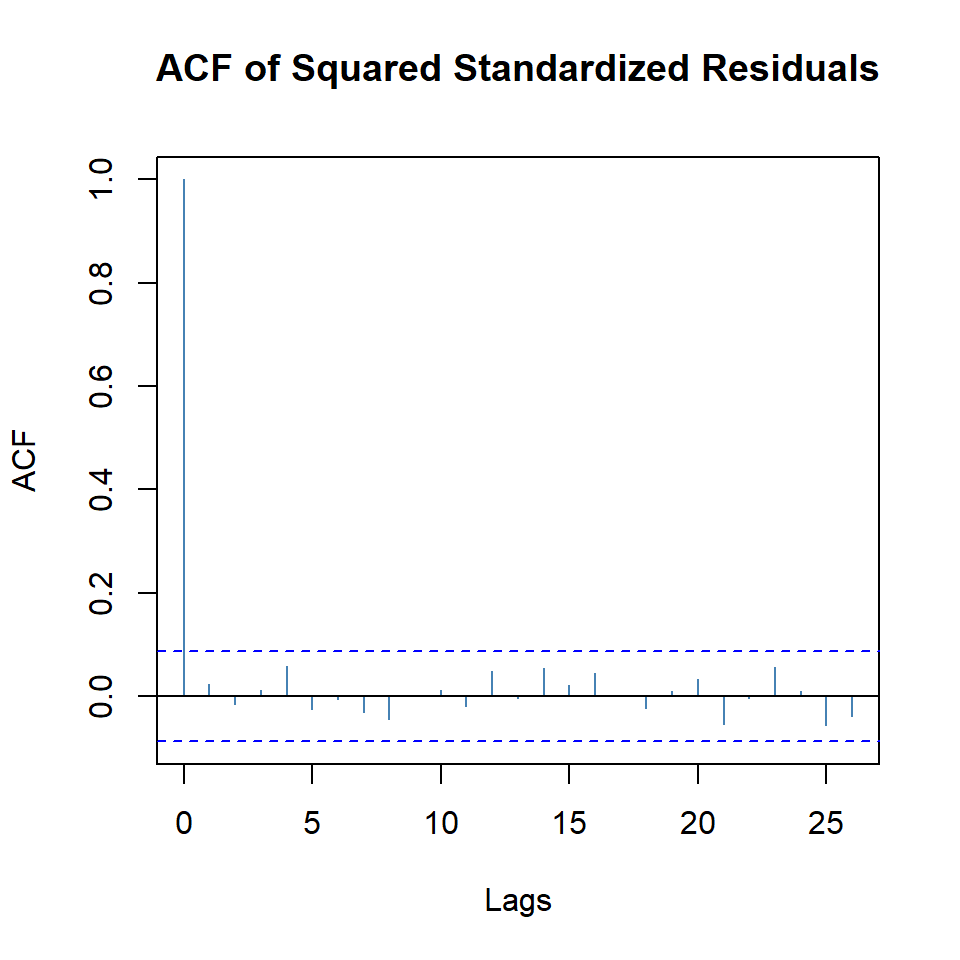

plot(arma.tgarch11.1,which=13)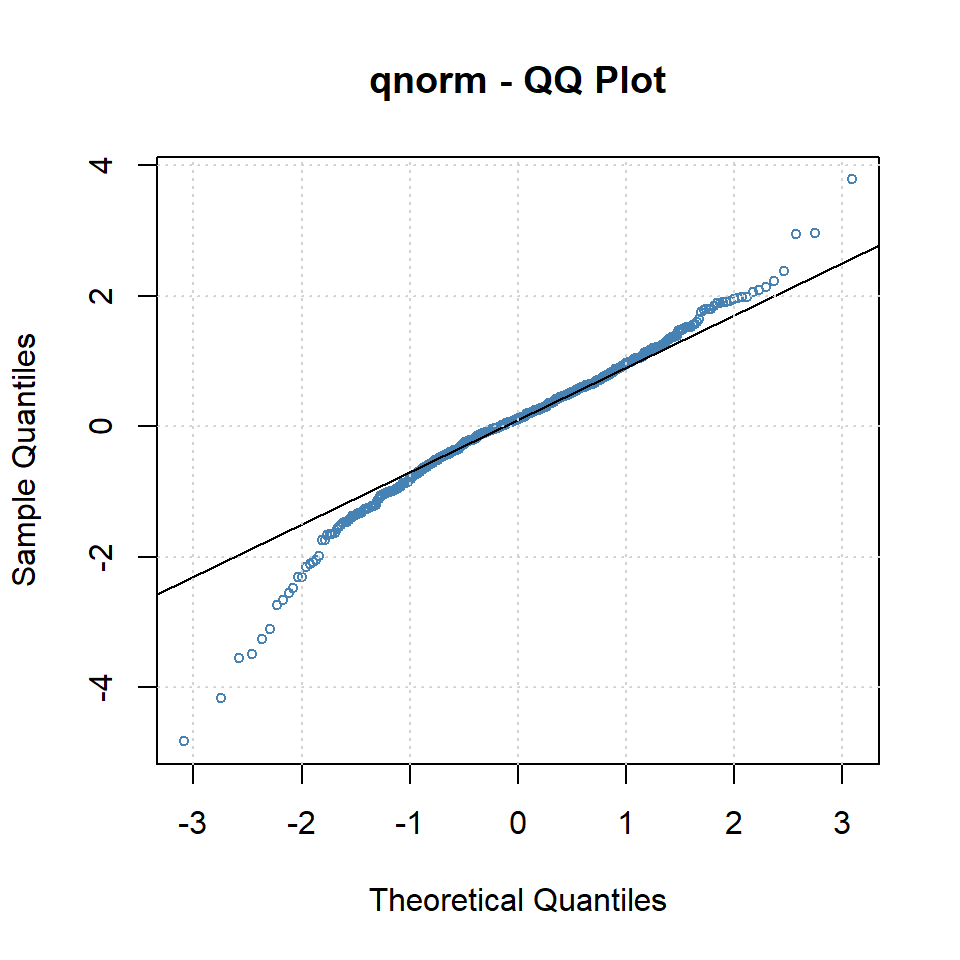

2.7 EGARCH

egarch11=ugarchfit(ugarchspec(mean.model=list(armaOrder=c(1,1)),
                        variance.model=list(model="eGARCH",garchOrder=c(1,1),
                        submodel=NULL,external.regressors=NULL, variance.targeting = FALSE)),r)
round(egarch11@fit$matcoef,4)

        Estimate  Std. Error  t value Pr(>|t|)
mu        0.0007      0.0004   1.8398   0.0658
ar1      -0.9057      0.0215 -42.0812   0.0000
ma1       0.9470      0.0170  55.8450   0.0000
omega    -0.5505      0.0490 -11.2374   0.0000
alpha1   -0.1584      0.0292  -5.4328   0.0000
beta1     0.9435      0.0051 183.8661   0.0000
gamma1    0.2534      0.0421   6.0259   0.0000

infocriteria(egarch11)

                      
Akaike       -7.175679
Bayes        -7.116675
Shibata      -7.176064
Hannan-Quinn -7.152526

plot(egarch11, which=11)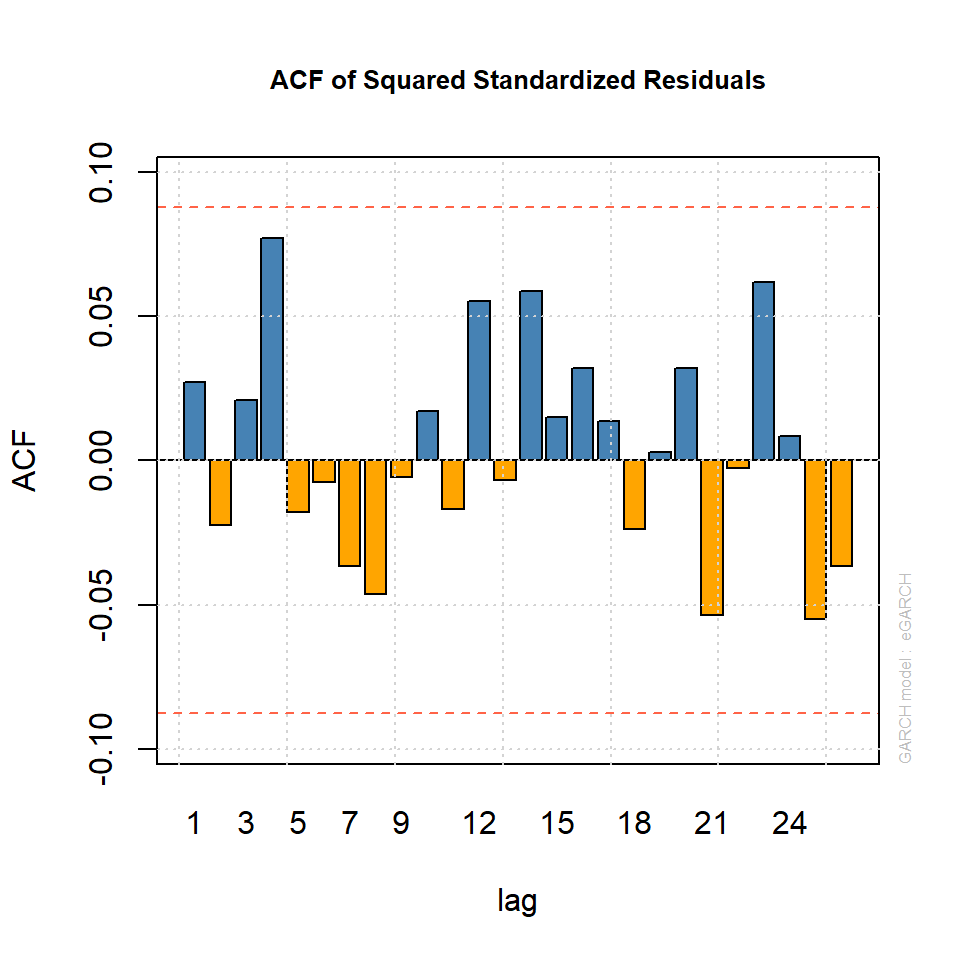

plot(egarch11, which=9)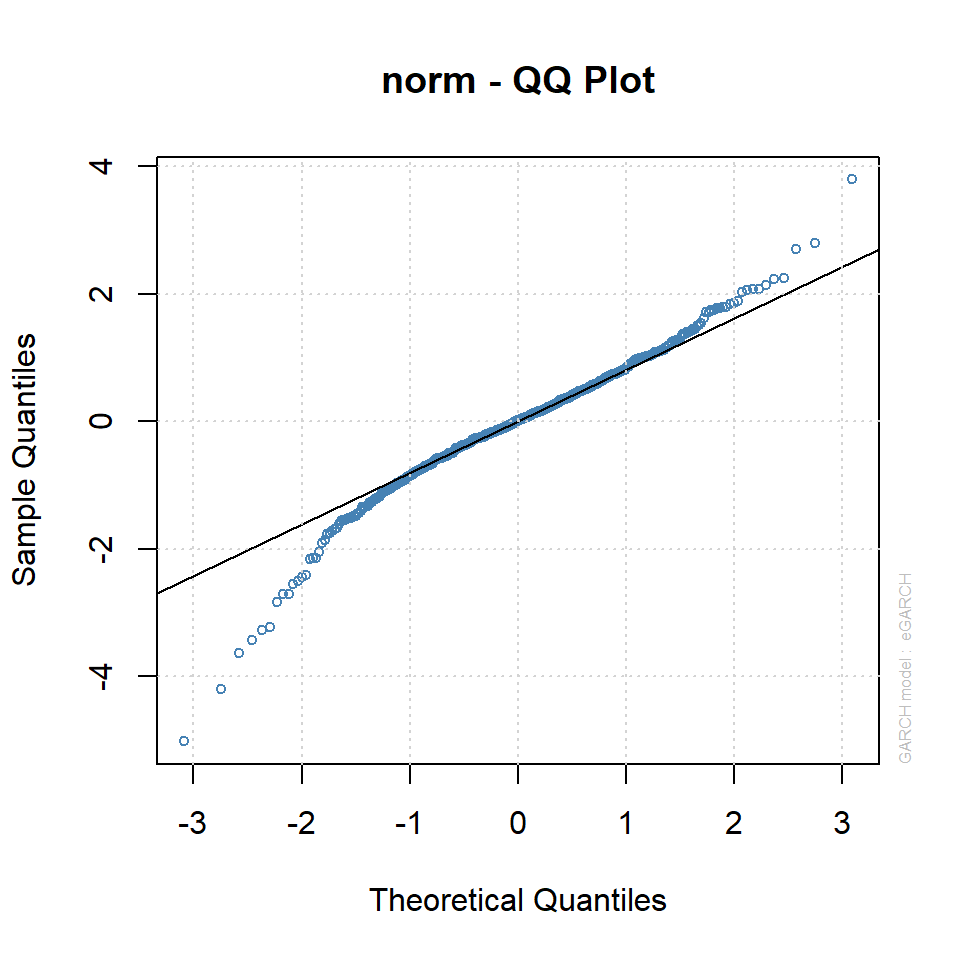

Todo parece indicar que TGARCH tiene mejor ajuste pero los residuales no son normales.

infocriteria(egarch11)

                      
Akaike       -7.175679
Bayes        -7.116675
Shibata      -7.176064
Hannan-Quinn -7.152526

arma.tgarch11.1@fit$ics

      AIC       BIC       SIC      HQIC 
-7.199735 -7.149160 -7.200019 -7.179890

2.8 Intentos con otras distribuciones

arma.tgarch11.snorm = garchFit(r~arma(1,1)+garch(1,1),delta=1,leverage=T,cond.dist="snorm",
                             data=r,trace=F,include.mean=F)
arma.tgarch11.ged = garchFit(r~arma(1,1)+garch(1,1),delta=1,leverage=T,cond.dist="ged",
                             data=r,trace=F,include.mean=F)
arma.tgarch11.sged = garchFit(r~arma(1,1)+garch(1,1),delta=1,leverage=T,cond.dist="sged",
                             data=r,trace=F,include.mean=F)
arma.tgarch11.std = garchFit(r~arma(1,1)+garch(1,1),delta=1,leverage=T,cond.dist="std",
                             data=r,trace=F,include.mean=F)
arma.tgarch11.sstd = garchFit(r~arma(1,1)+garch(1,1),delta=1,leverage=T,cond.dist="sstd",
                             data=r,trace=F,include.mean=F)

arma.tgarch11.snorm@fit$ics

      AIC       BIC       SIC      HQIC 
-7.220865 -7.161861 -7.221250 -7.197712

arma.tgarch11.ged@fit$ics

      AIC       BIC       SIC      HQIC 
-7.269333 -7.210328 -7.269717 -7.246179

arma.tgarch11.sged@fit$ics

      AIC       BIC       SIC      HQIC 
-7.285290 -7.217856 -7.285791 -7.258829

arma.tgarch11.std@fit$ics

      AIC       BIC       SIC      HQIC 
-7.268835 -7.209830 -7.269220 -7.245681

arma.tgarch11.sstd@fit$ics

      AIC       BIC       SIC      HQIC 
-7.282483 -7.215050 -7.282985 -7.256022

El modelo ganador es arma.tgarch11.sged.

round(arma.tgarch11.sged@fit$matcoef, 4)

        Estimate  Std. Error  t value Pr(>|t|)
ar1      -0.8105      0.1250  -6.4858   0.0000
ma1       0.8659      0.1257   6.8903   0.0000
omega     0.0004      0.0001   3.1025   0.0019
alpha1    0.1495      0.0399   3.7443   0.0002
gamma1    0.6927      0.2073   3.3415   0.0008
beta1     0.8383      0.0398  21.0874   0.0000
skew      0.8681      0.0450  19.3077   0.0000
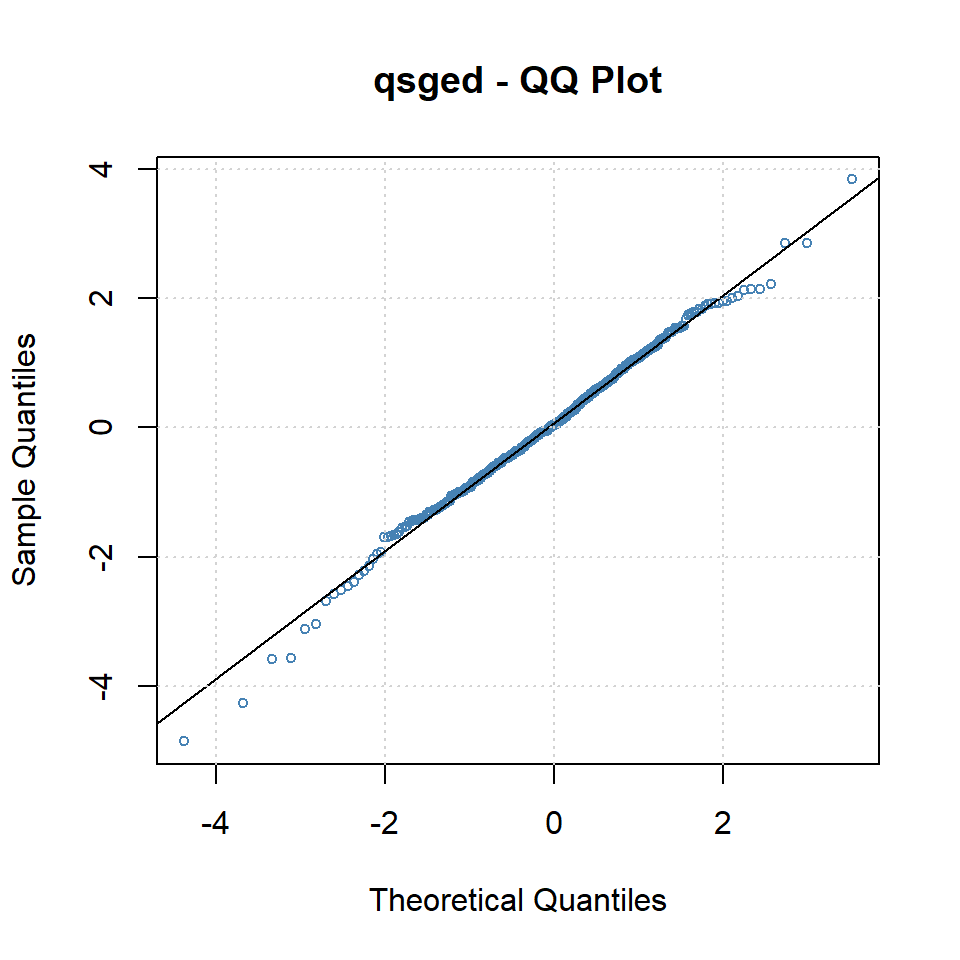
shape     1.1957      0.1017  11.7524   0.0000

plot(arma.tgarch11.sged, which = 10)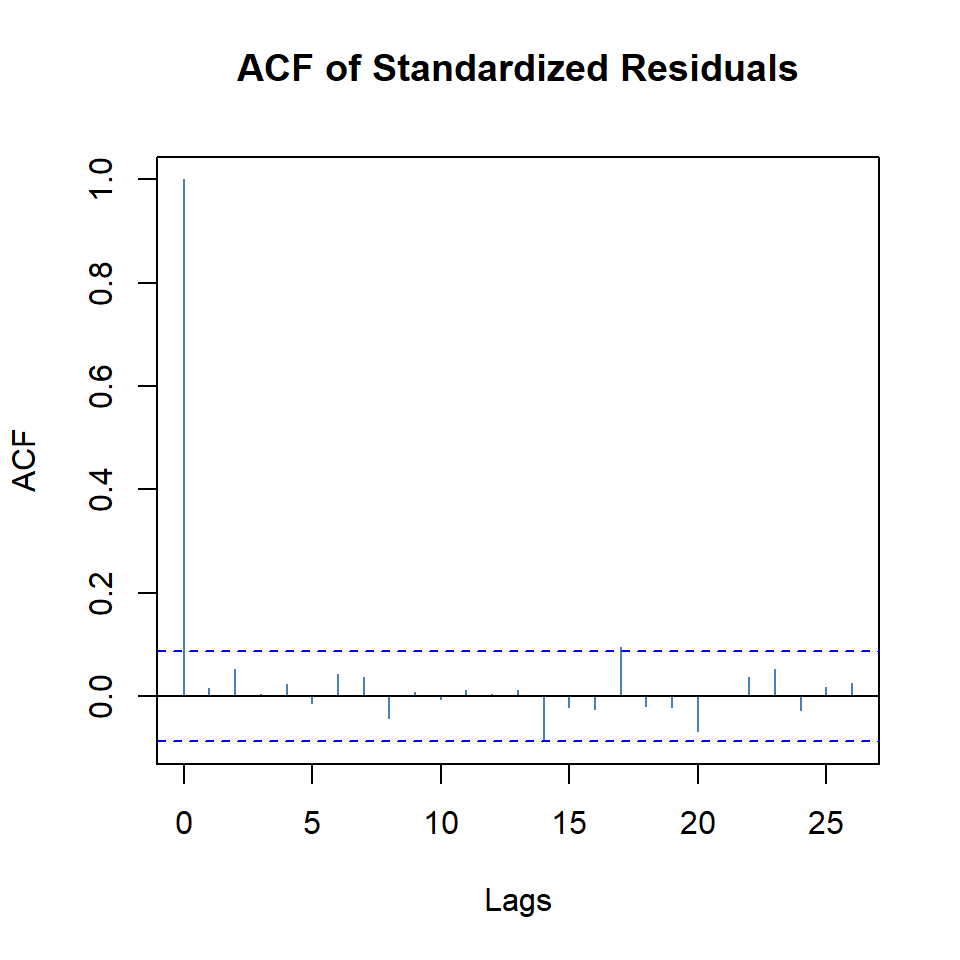

plot(arma.tgarch11.sged, which = 11)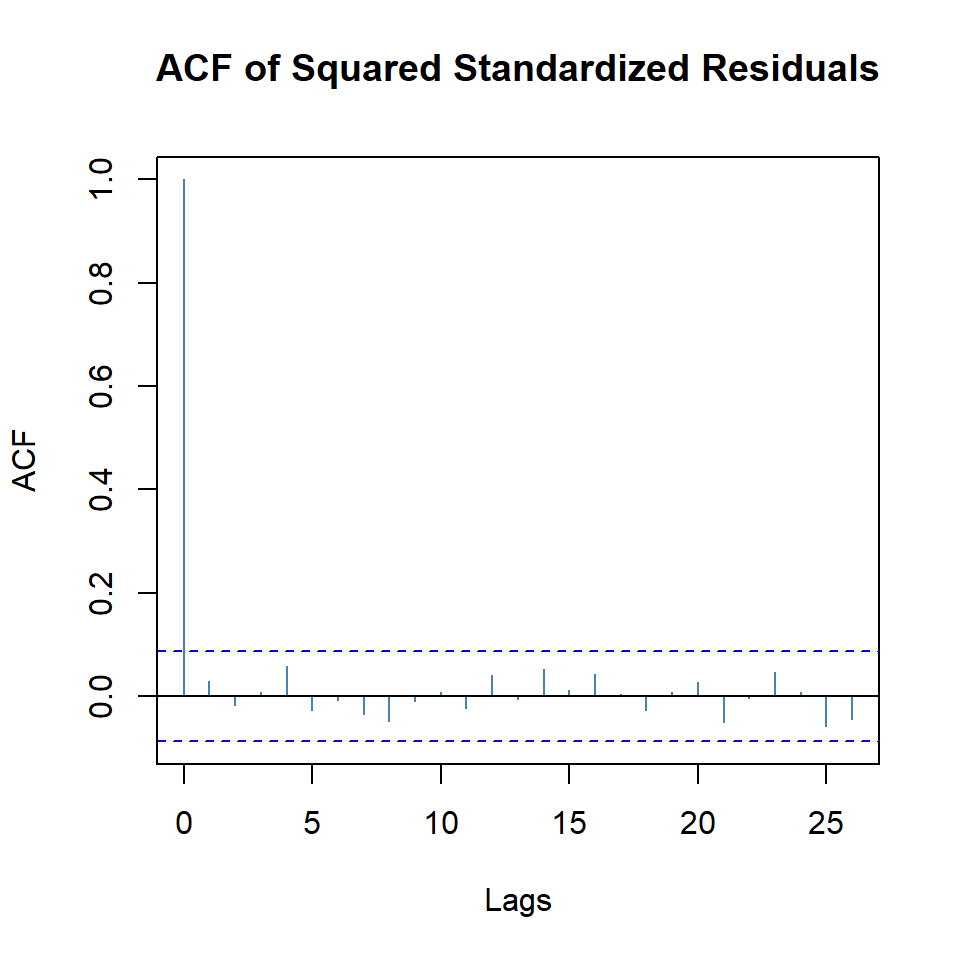

plot(arma.tgarch11.sged, which = 13)

1 librerías

2 Ejemplo: promedio diario industrial Dow Jone

2.1 Retornos

2.2 auto.arima

2.3 ARMA(1,1)+ARCH(1)

2.4 ARMA(1,1)+GARCH(1,1)

2.5 GARCH(1,1)

2.6 T-GARCH

2.7 EGARCH

2.8 Intentos con otras distribuciones

2.2 `auto.arima`