[1] "DJI"Tema 4: Modelos no lineales(1)
Introducción
Contenido
Introducción
ARCH
GARCH
Extensiones del modelo GARCH: EGARCH y TGARCH
Distribuciones simétricas y asimétricas
Introducción
- En la práctica, se observan fenómenos con variancia condicional que evoluciona con el tiempo y los modelos ARIMA no son adecuados para estos fenómenos.
- La aplicación más utilizada y conocida es en las series financieras.
- Existe una variedad de modelos no lineales en la literatura.
- Vamos a enfocarnos en la clase de modelos GARCH:
- ARCH (AutoRegressive Conditional Heteroscedastic): Modelos autoregresivos con heteroscedasticidad condicional.
- GARCH (Generalized AutoRegressive Conditional Heteroscedastic): Modelos autoregresivos con heteroscedasticidad condicional generalizada.
- Extensiones del modelo GARCH: EGARCH y TGARCH.
Algunos modelos no lineales
- De manera general, el análisis de modelos no lineales suponen que los errores o innovaciones \(a_t\) son i.i.d. y el modelo tiene la siguiente forma: \[X_t= g(a_{t-1},a_{t-2},...)+a_{t}h(a_{t-1},a_{t-2},...),\] en donde
- \(g(\cdot)\) es la media condicional, y
- \(h^2(\cdot)\) es la variancia condicional.
- Se dice que el modelo es
- no lineal en media, si \(g(\cdot)\) es no lineal.
- no lineal en variancia, si \(h^2(\cdot)\) es no lineal.
Ejemplo 1
Los modelos ARMA (bajo el supuesto de estacionariedad) pueden ser representados por: \[X_t= \sum\limits_{i=0}^\infty \xi_i a_{t-i} = \sum\limits_{i=1}^\infty \xi_i a_{t-i} + a_{t}\]
Note que \(g(\cdot)=\sum\limits_{i=0}^\infty \xi_i a_{t-i}\) y \(h(\cdot)=1\) son lineales. Entonces, un modelo ARMA es lineal.
Ejemplo 2
- El modelo: \[X_t=a_t+\alpha a_{t-1}^2\] es no lineal en media porque \(g(\cdot)=\alpha a_{t-1}^2\) y lineal en variancia \(h(\cdot)=1\).
Ejemplo 3
- El modelo ARCH(1) \[X_t= a_t \sqrt{\alpha X_{t-1}^2}\] es no lineal en variancia porque \(g(\cdot)=0\) y \(h(\cdot)=\sqrt{\alpha X_{t-1}^2}\) y \(X_{t-1}\) depende de \(a_{t-1}\).
Ejemplo 4
- Modelos polinomiales tienen la función \(g(\cdot)\) como
\[g(a_{t-1},a_{t-2},...)=\sum\limits_{i=1}^\infty c_i a_{t-i}+\sum\limits_{i=1}^\infty \sum\limits_{j=1}^\infty b_{ij} a_{t-i} a_{t-j}+...,\] Es una expansión de Volterra, involucrando términos lineales, bilineales,… de las innovaciones.
Los modelos ARCH
Los modelos ARCH (AutoRegressive Conditional Heteroscedastic), o modelos autorregresivos con heteroscedasticidad condicional, fueron propuestos por Engle (1982).
Robert F. Engle recibió Premio Nobel de Economía por los análisis de ARCH para datos de series temporales económicos.
La idea básica del modelo es un proceso estacionario que tienen la variancia marginal constante, pero la variancia condicionada a sus valores pasados no lo es.
Estos procesos fueron propuestos para explicar ciertas propiedades que no pueden ser explicados por los modelos ARIMA y que son muy frecuentes en datos financieros y ambiantales de alta frecuencia (datos diarios, horarios, etc.).
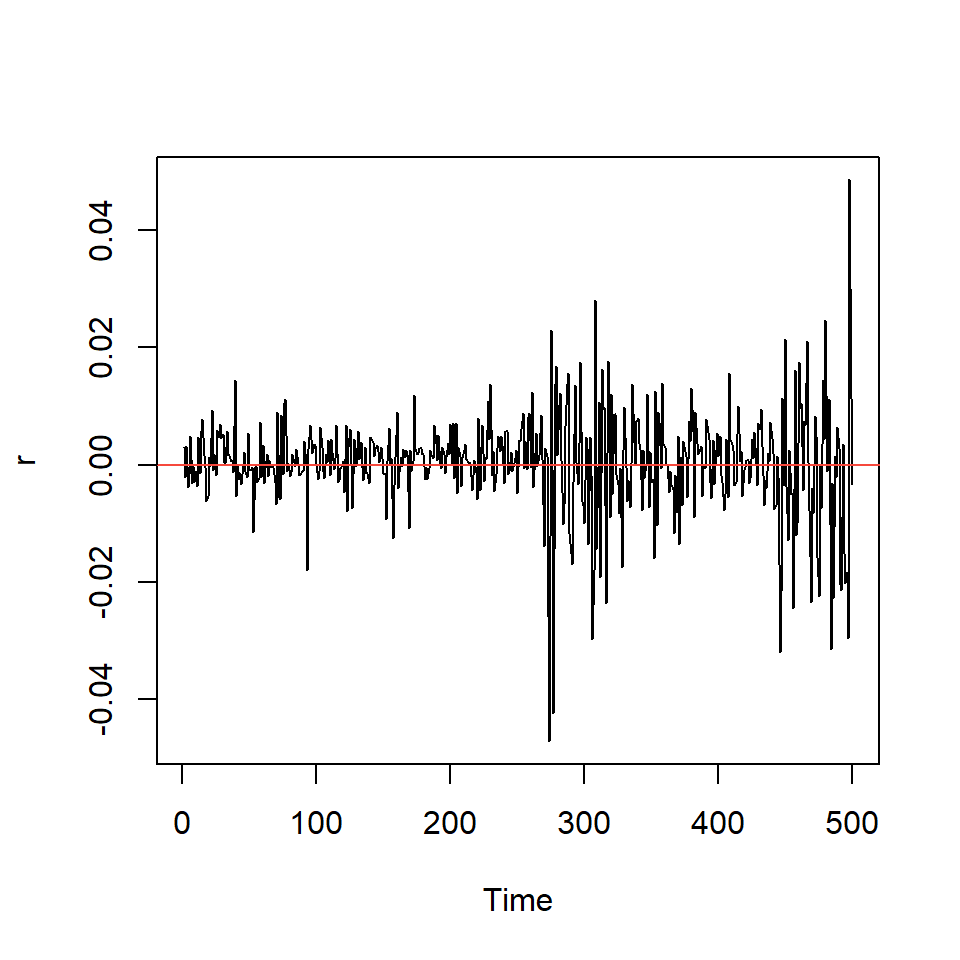
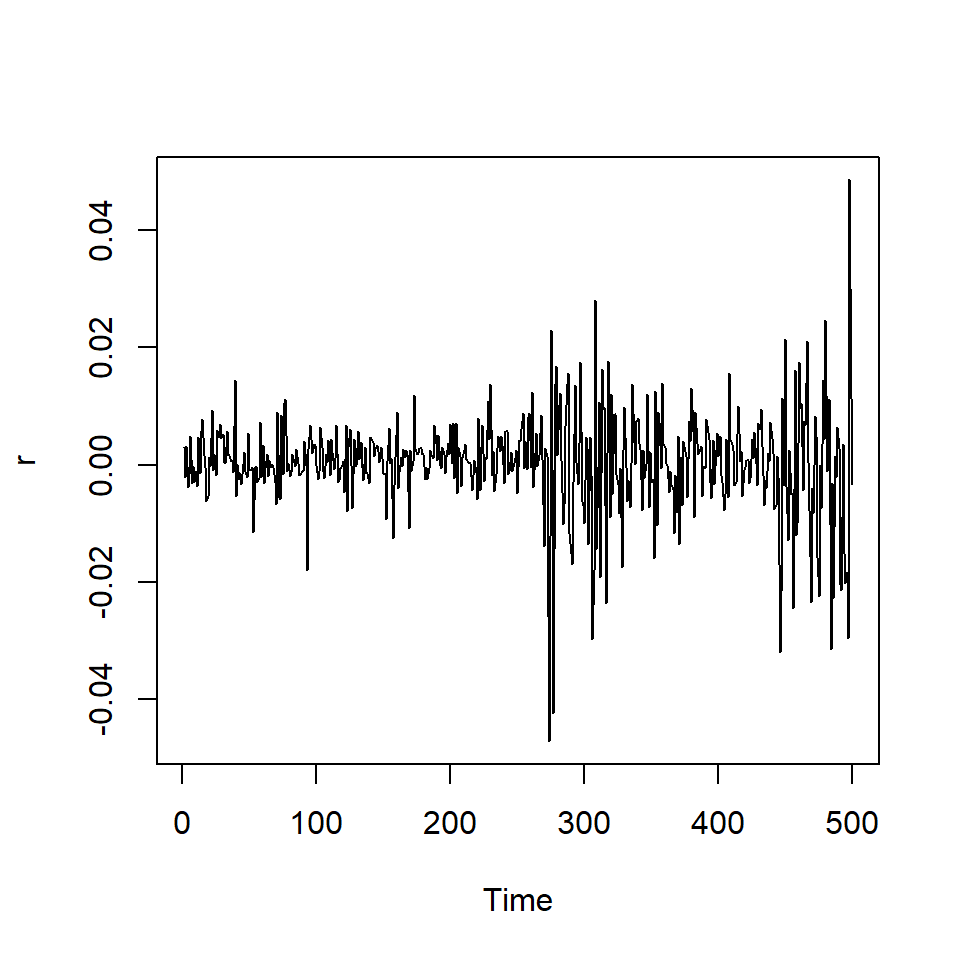
Retornos
- Suponga que \(X_t\) es el valor de un activo en el tiempo \(t\), el retorno \(r_t\) en el tiempo \(t\) es:
\[r_t=\frac{X_t-X_{t-1}}{X_{t-1}}\]
- Despejando la expresión anterior:
\[X_t=(1+r_t)X_{t-1}\] \[\Rightarrow \ln X_t=\ln (1+r_t)+ \ln X_{t-1}\] \[\Rightarrow \nabla \ln X_t = \ln X_t - \ln X_{t-1}=\ln (1+r_t) \approx r_t,\] si \(r_t\) son cambios porcentuales pequeños.
Nota
- Recuerde que para una función \(f(x)\), el polinomio de Taylor es una aproximación polinómica de una función n veces derivable en un punto \(a\). Concretamente:
\[f(x) \approx f(a) + f'(a) (x-a) + \frac{f''(a)}{2!}(x-a)^2 + ...+ \frac{f^{(n)}(a)}{n!}(x-a)^n\]
De esta forma, \[\nabla \ln X_t = \ln X_t - \ln X_{t-1}=\ln (1+r_t) = f(r_t) \approx r_t,\]
A partir de aquí, llamamos \(r_t\) o \(\nabla \ln X_t\) como retornos.
En finanzas, la variancia condicional del retorno financiero de una cartera es una medida de riesgo de una cartera (Value at Risk - VAR).
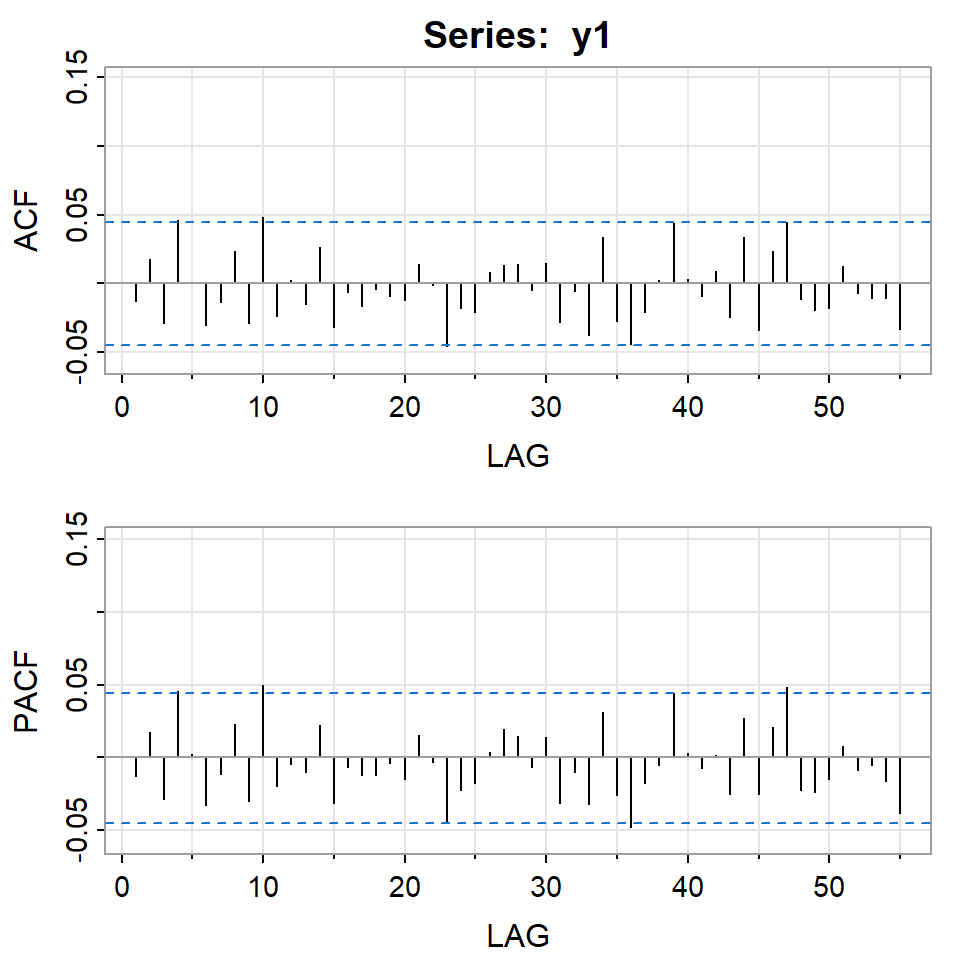
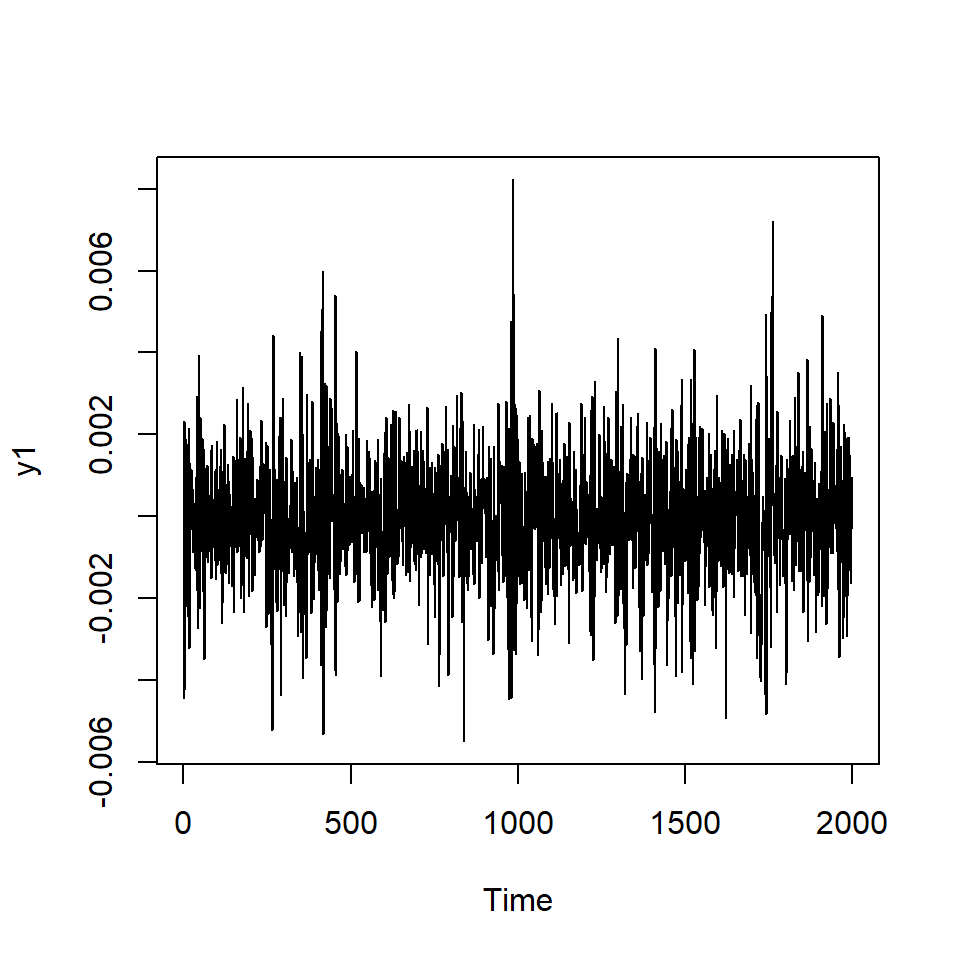
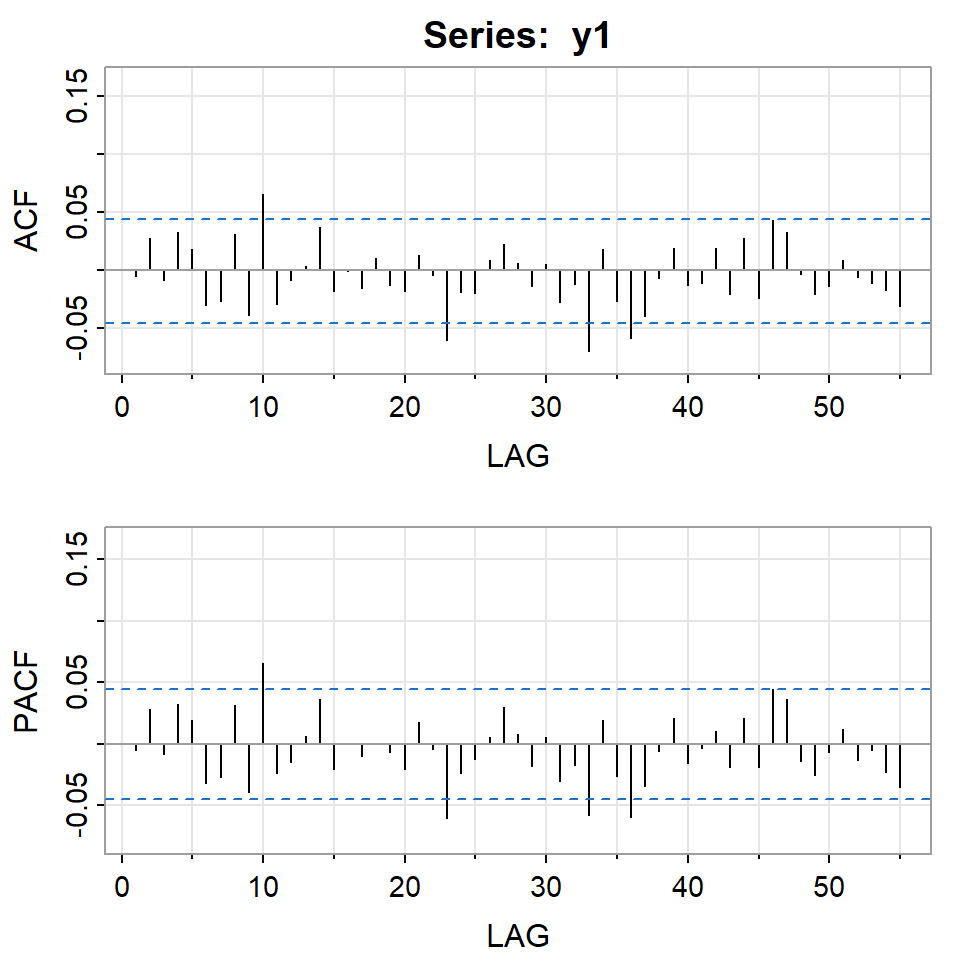
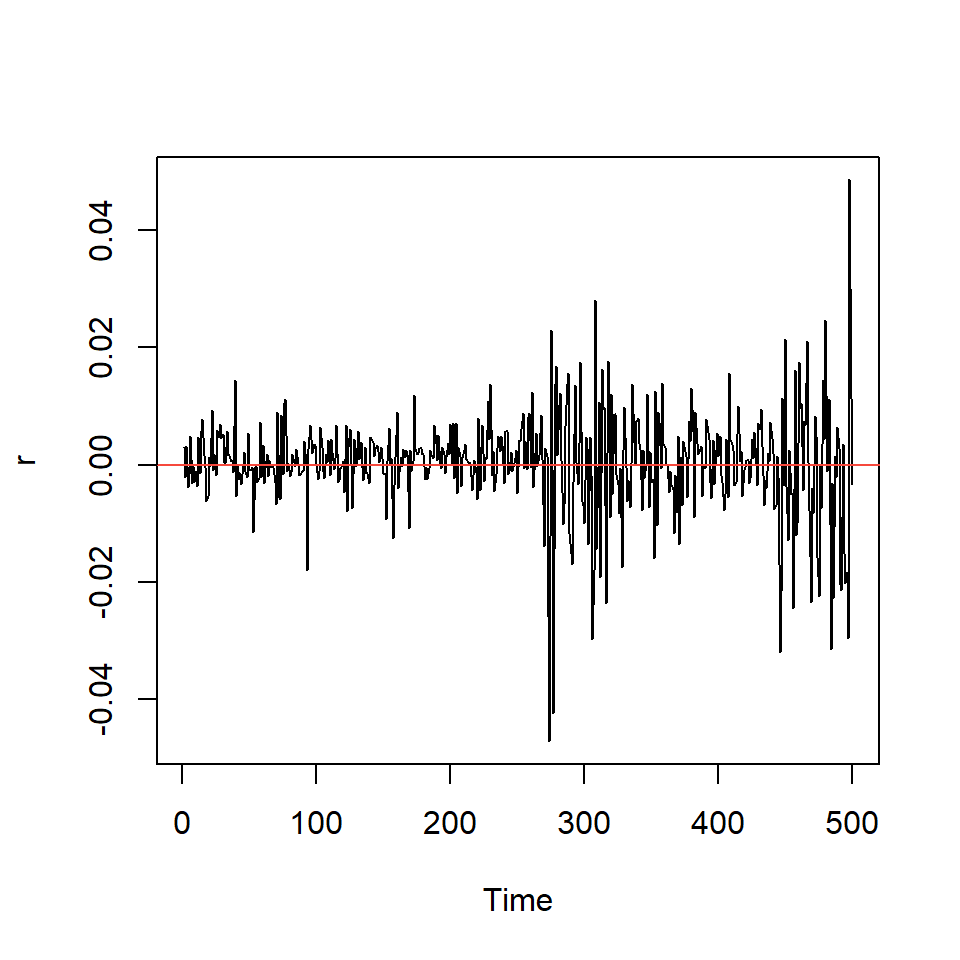
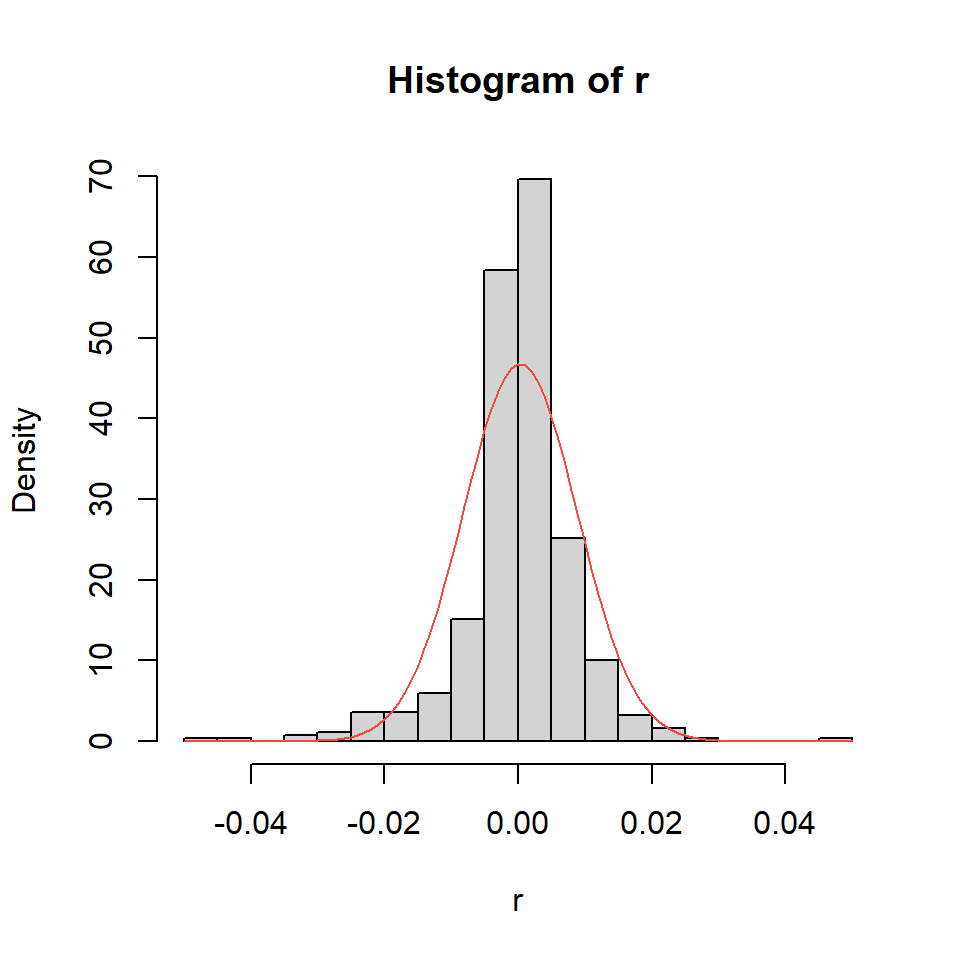
En un mercado eficiente, el retorno esperado debería ser cero, y así debería comportarse como un proceso de ruido blanco.
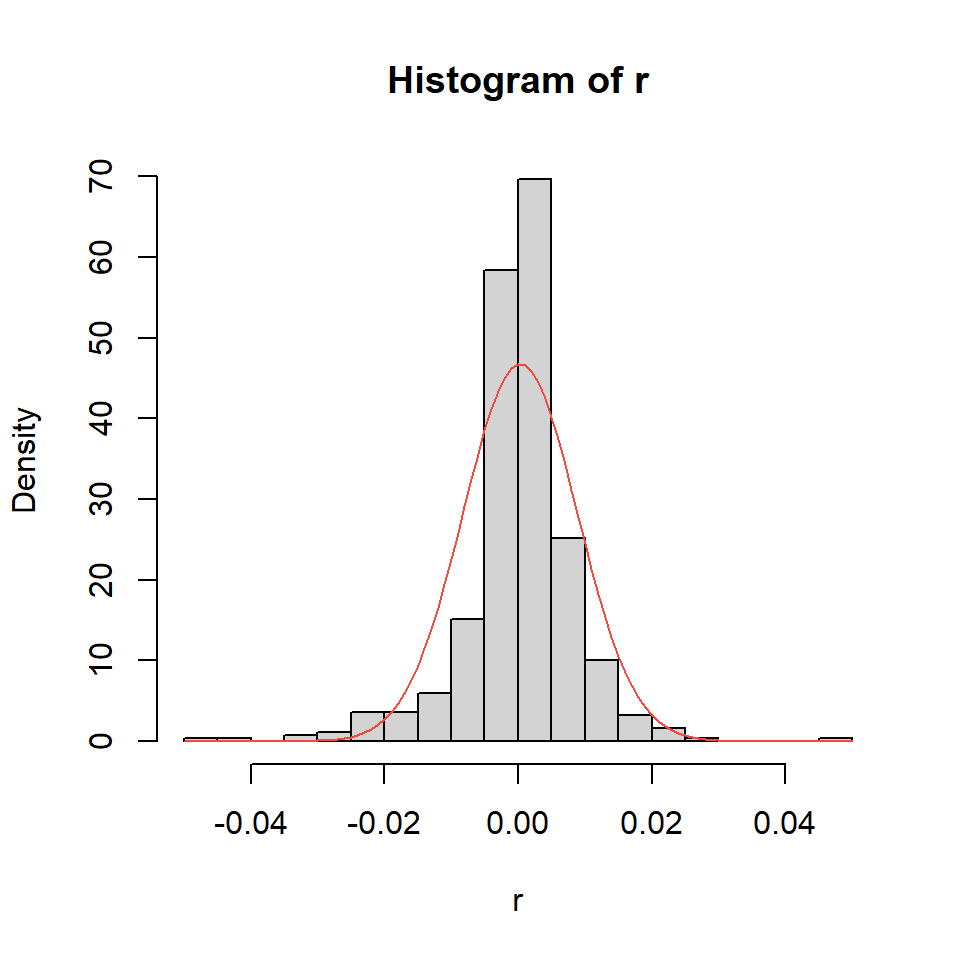
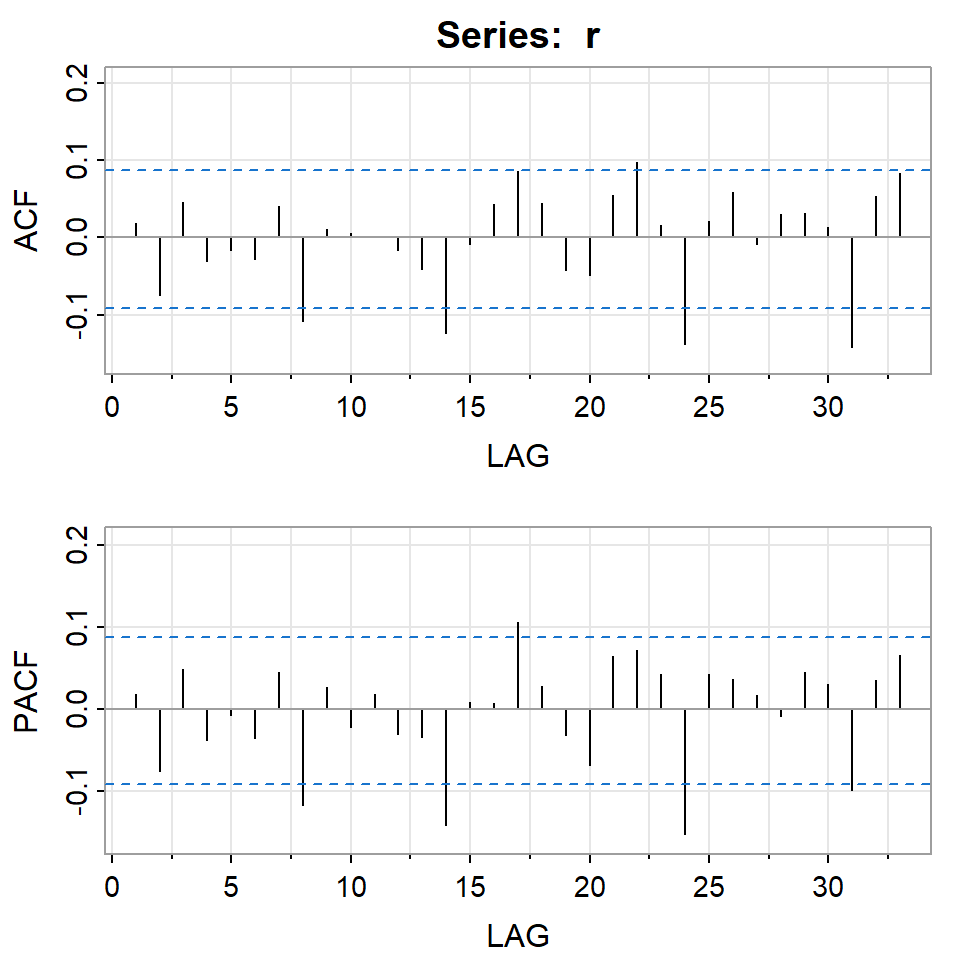
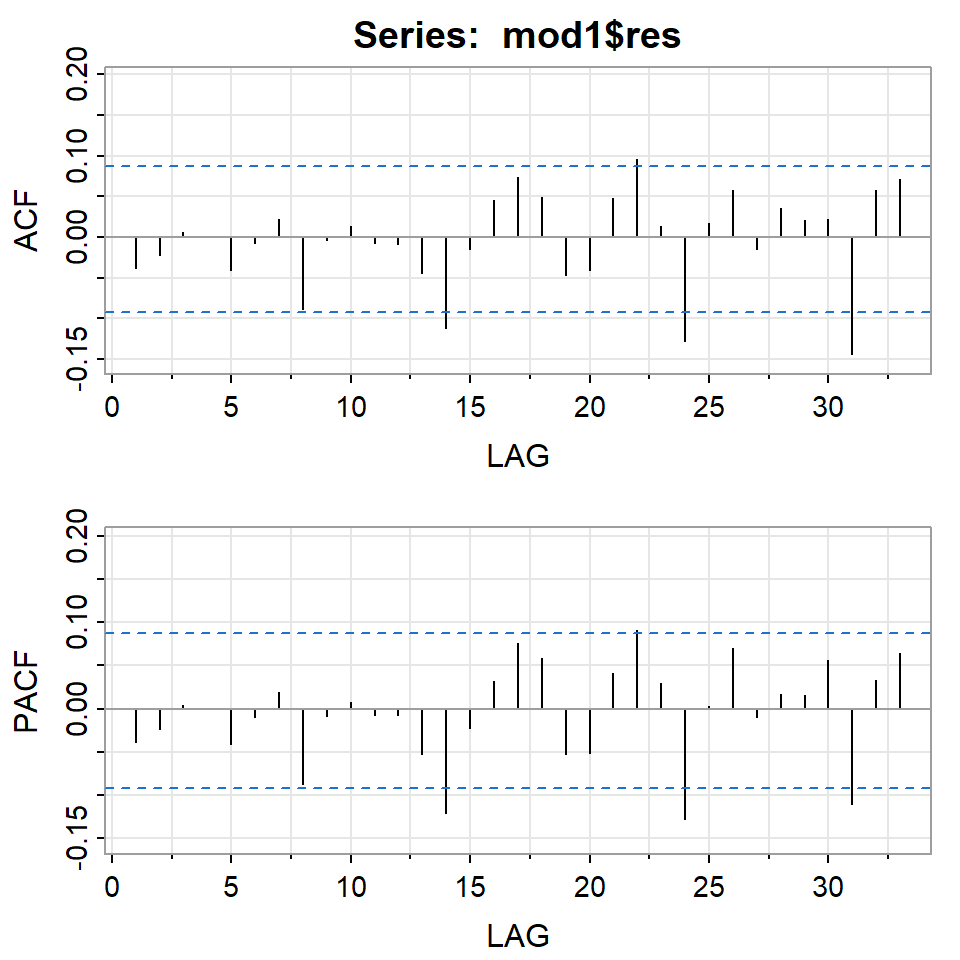
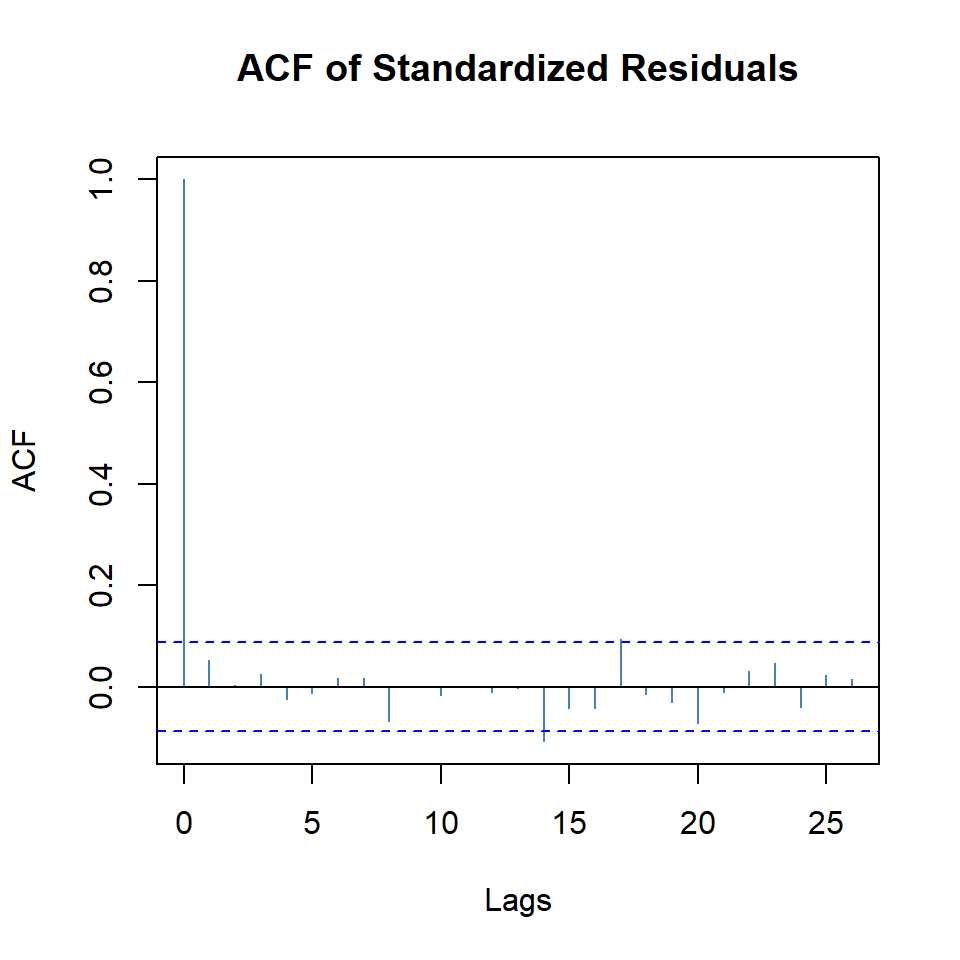
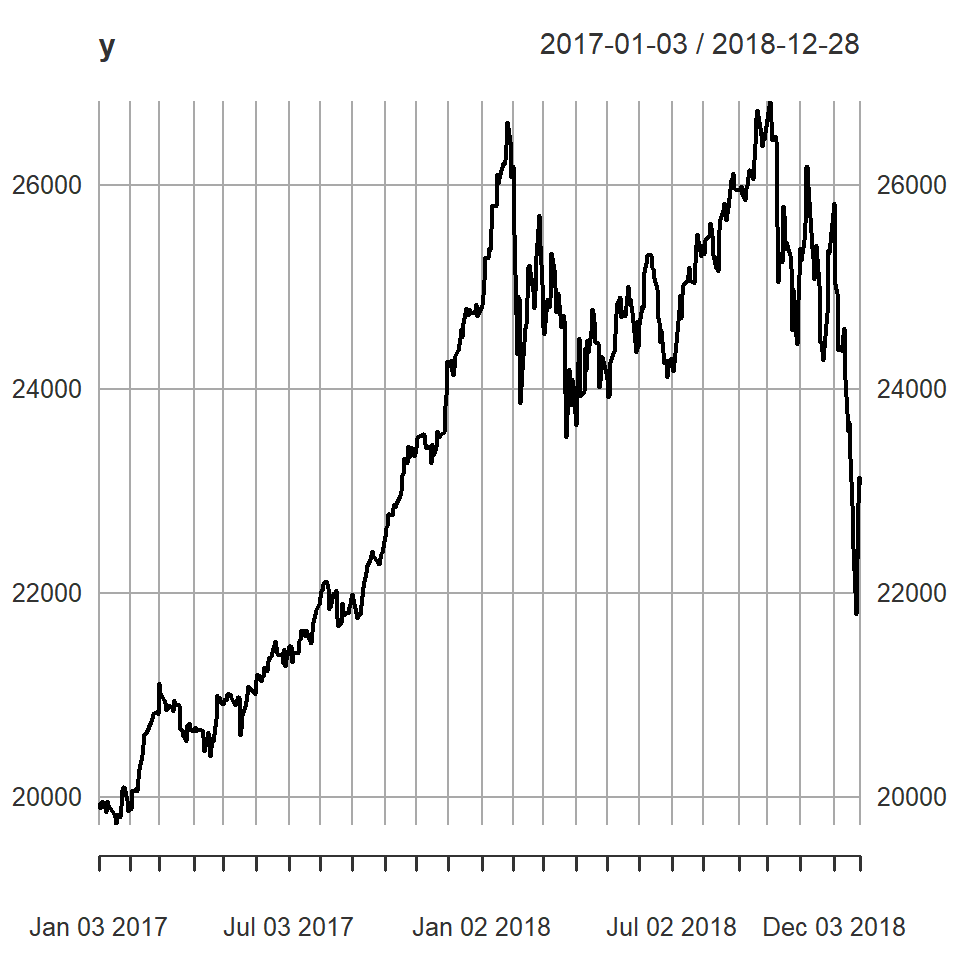
Ejemplo: promedio diario industrial Dow Jone
[,1] [,2] [,3] [,4] [,5] [,6] [,7] [,8] [,9] [,10] [,11] [,12] [,13]
ACF 0.02 -0.07 0.05 -0.03 -0.02 -0.03 0.04 -0.11 0.01 0.01 0.00 -0.02 -0.04
PACF 0.02 -0.08 0.05 -0.04 -0.01 -0.04 0.04 -0.12 0.03 -0.02 0.02 -0.03 -0.03
[,14] [,15] [,16] [,17] [,18] [,19] [,20] [,21] [,22] [,23] [,24] [,25]
ACF -0.12 -0.01 0.04 0.09 0.05 -0.04 -0.05 0.05 0.10 0.02 -0.14 0.02
PACF -0.14 0.01 0.01 0.11 0.03 -0.03 -0.07 0.06 0.07 0.04 -0.15 0.04
[,26] [,27] [,28] [,29] [,30] [,31] [,32] [,33]
ACF 0.06 -0.01 0.03 0.03 0.01 -0.14 0.05 0.08
PACF 0.04 0.02 -0.01 0.04 0.03 -0.10 0.04 0.07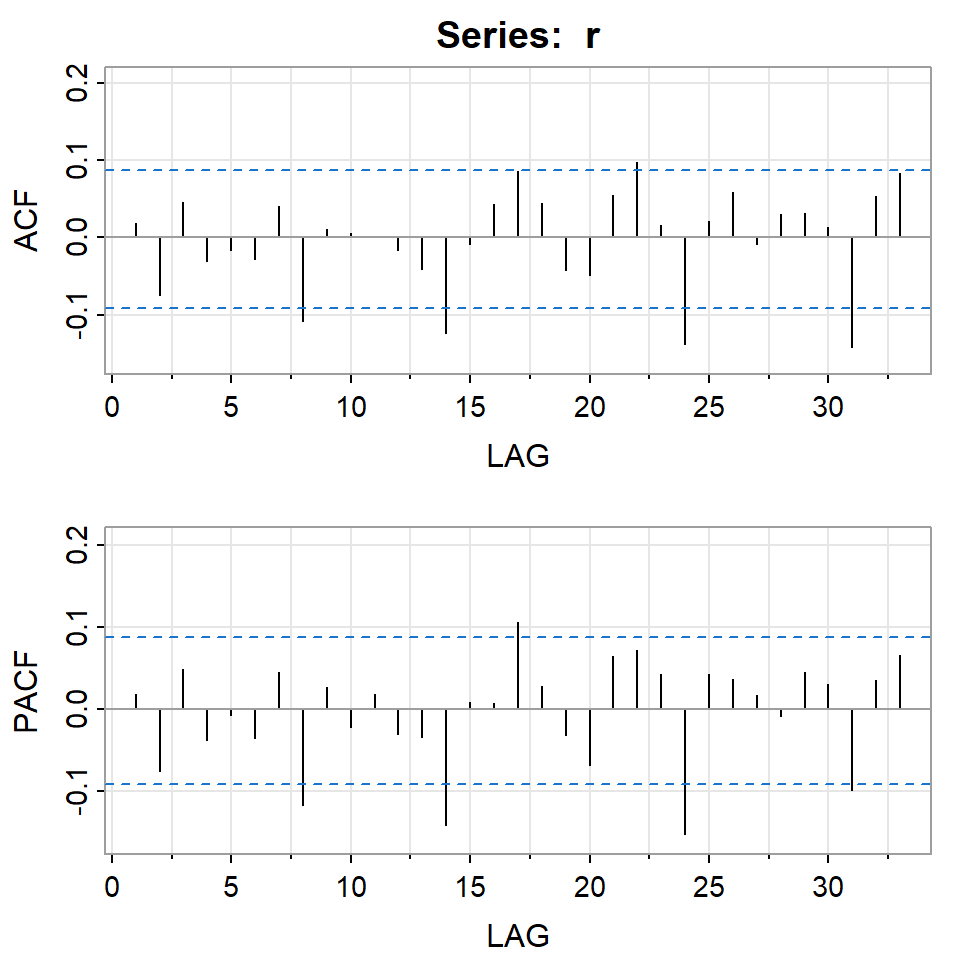
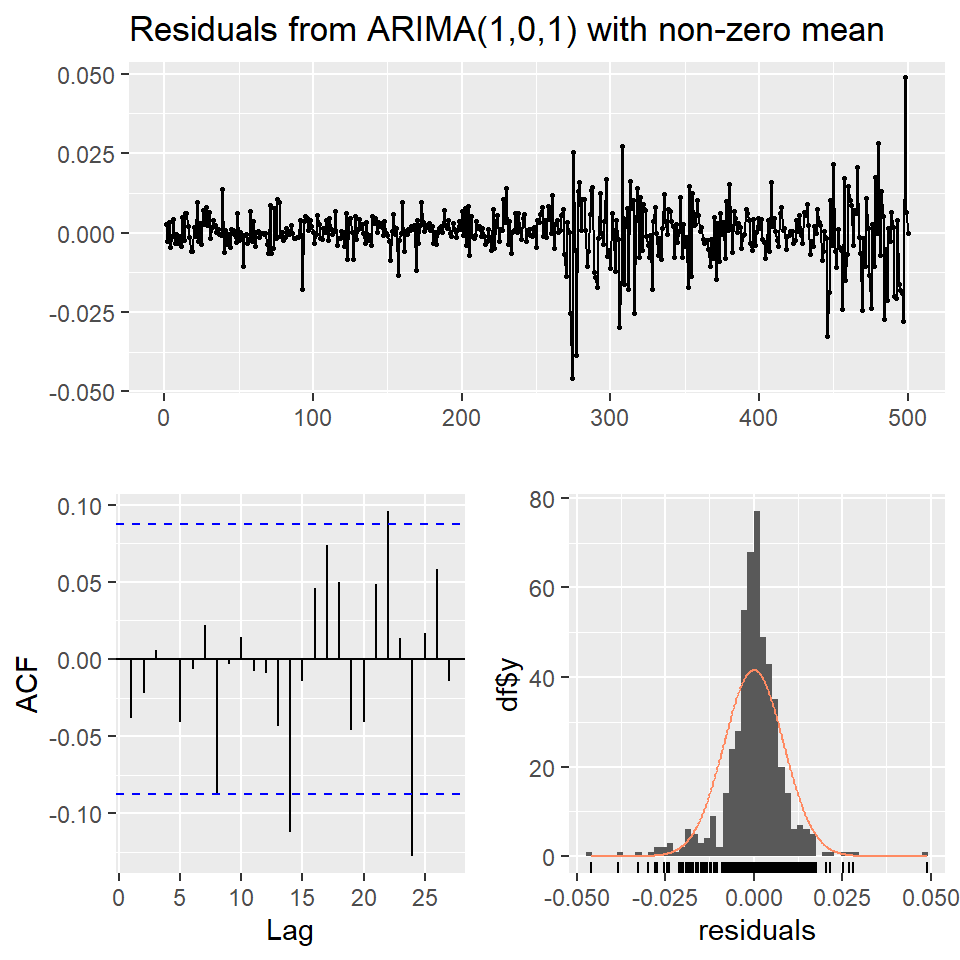
Series: r
ARIMA(1,0,1) with non-zero mean
Coefficients:
ar1 ma1 mean
-0.8613 0.9456 3e-04
s.e. 0.0418 0.0259 4e-04
sigma^2 = 7.121e-05: log likelihood = 1679.38
AIC=-3350.76 AICc=-3350.68 BIC=-3333.9
Training set error measures:
ME RMSE MAE MPE MAPE MASE
Training set 1.210921e-05 0.008413378 0.005502822 98.24685 154.1698 0.7121837
ACF1
Training set -0.03847749ARCH
Contenido
Introducción
ARCH
GARCH
Extensiones del modelo GARCH: EGARCH y TGARCH
Distribuciones simétricas y asimétricas
ARCH
- Modelo ARCH(1):
\[X_t=\sqrt{h_t} \epsilon_t\] \[h_t= \alpha_0 +\alpha_1 X_{t-1}^2\] en donde \(\epsilon_t\) es ruido blanco gaussiano estándar, i.e. \(\epsilon_t \overset{iid}{\sim} N(0,1)\), y \(\alpha_0>0,\alpha_1 \geq 0\).
- La distribución condicional de \(X_t\) dado \(X_{t-1}\) es
\[X_t|X_{t-1} \sim N(0,\alpha_0 +\alpha_1 X_{t-1}^2)\]
Recordatorio: las propiedades de la esperanza y variancia condicional.
\[E[Y]=E[E(Y|X)]~~y~~Var[Y]=E[Var(Y|X)]+Var[E(Y|X)]\]
Defina \(\mathcal{F}_s= \left\lbrace X_{s},X_{s-1},... \right\rbrace\) como la información disponible hasta el período \(s\). Podemos calcular la media, variancia y autocorrelación incondicional de la serie:
Propiedades:
- \(E(X_t)=E \left\lbrace E \left[ X_t| \mathcal{F}_{t-1} \right] \right\rbrace=0\)
- \(Var(X_t)= E(X_t^2)=E \left\lbrace E \left[ X_t^2| \mathcal{F}_{t-1} \right] \right\rbrace=E(\alpha_0+\alpha_1 X_{t-1}^2)\) \(=\alpha_0+\alpha_1 E(X_{t-1}^2)\)
Si el proceso es estacionario, entonces para todo \(t\), \(E(X_{t}^2)=E(X_{t-1}^2)=Var(X_t)\) \[\Rightarrow Var(X_t)=\frac{\alpha_0}{1-\alpha_1}\] con \(0 \leq \alpha_1<1\).
- \(Cov(X_{t+k},X_t)=E(X_{t+k} X_t), k \geq 1,\)
\(=E\left\lbrace E \left[ X_{t+k}X_t| \mathcal{F}_{t+k-1} \right] \right\rbrace=E\left\lbrace X_t~ E \left[ X_{t+k}| \mathcal{F}_{t+k-1} \right] \right\rbrace\)
\(= E\left\lbrace X_t~ E \left[ \sqrt{h_{t+k}}\epsilon_{t+k}| \mathcal{F}_{t+k-1} \right] \right\rbrace=0\)
Por lo tanto, \(\gamma_X(k)=0, k \geq 1\). En otras palabras, \(X_t\) es una secuencia de variables aleatorias no correlacionadas (ruido blanco) con variancia \(\frac{\alpha_0}{1-\alpha_1}\).
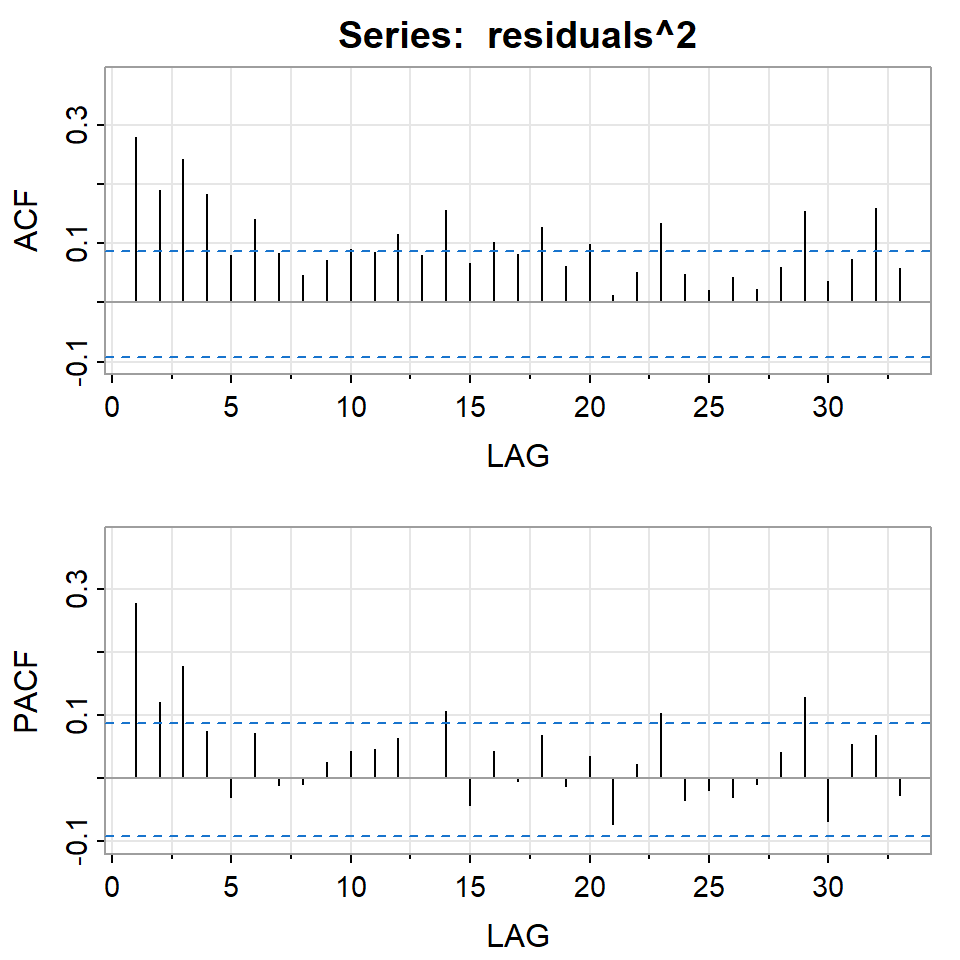
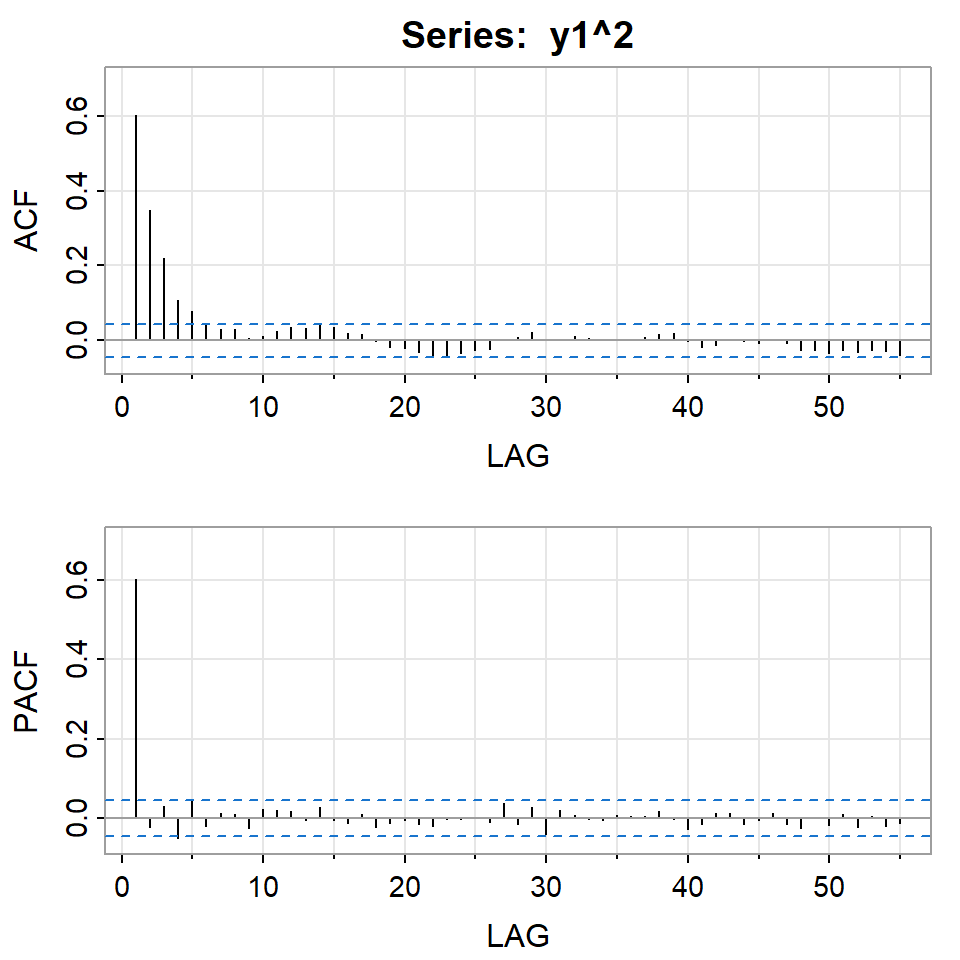
- Se puede demostrar que la kurtosis es \[K=3\frac{1-\alpha_1^2}{1-3 \alpha_1^2}>3.\] El modelo ARCH(1) es leptocúrtico ya que las colas son más pesadas que una distribución normal.
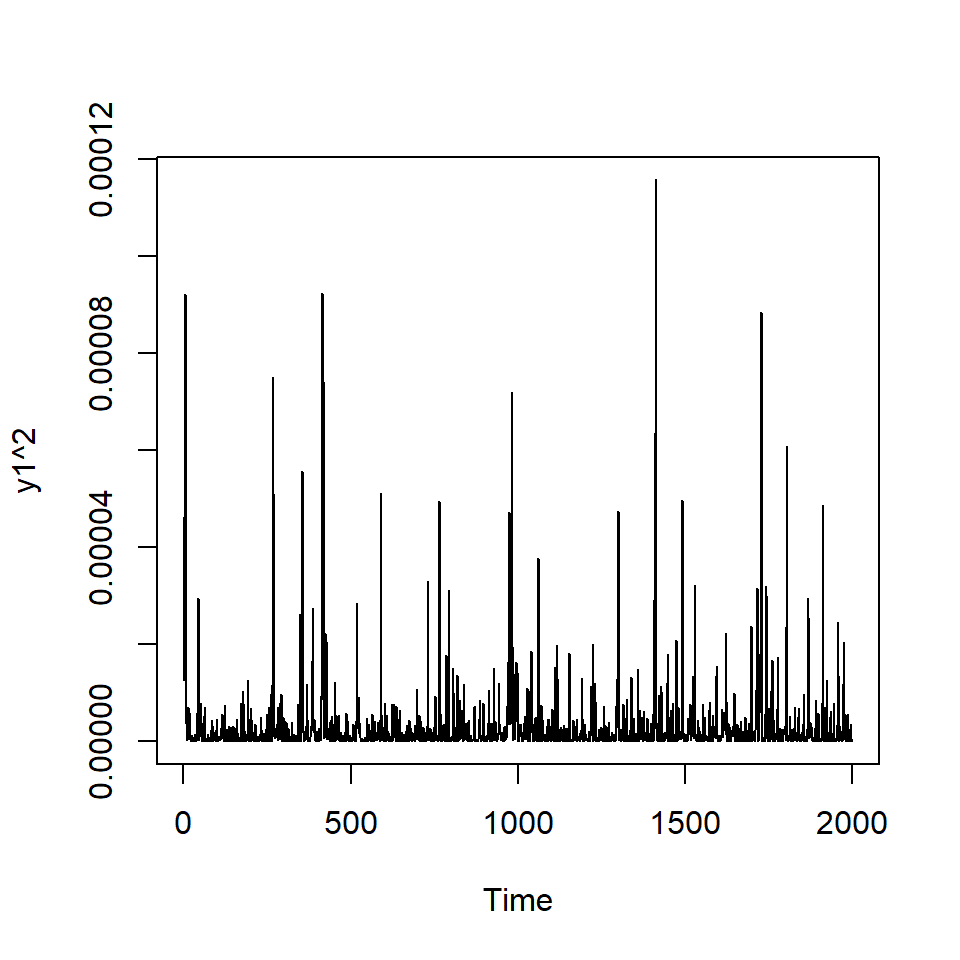
Simulación de ARCH(1) con \(\alpha_0=0.01\), \(\alpha_1=0.8\)
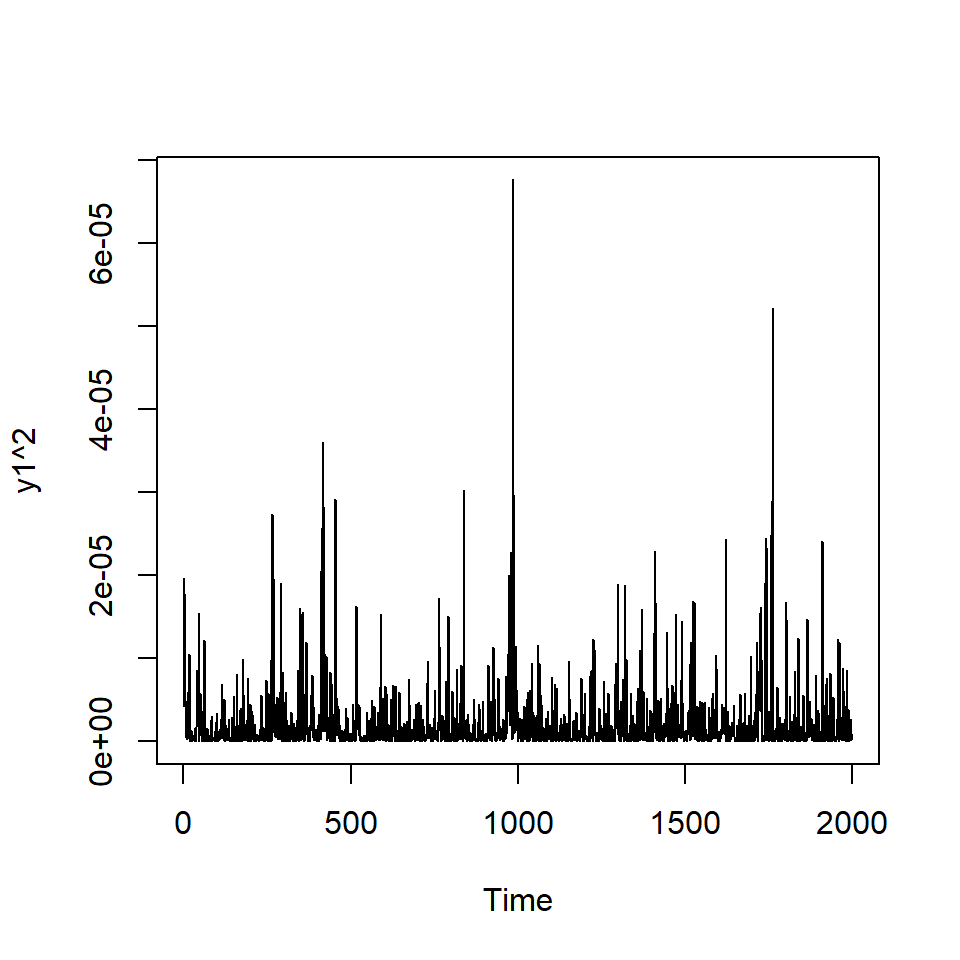
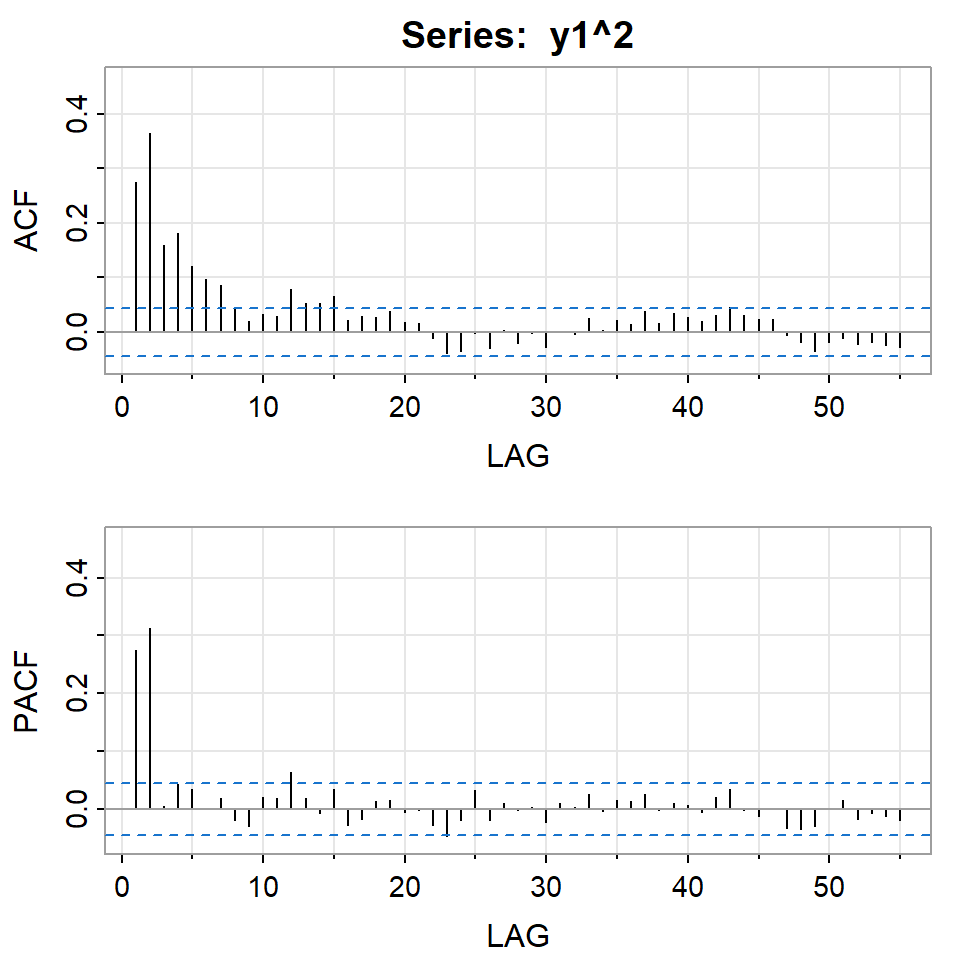
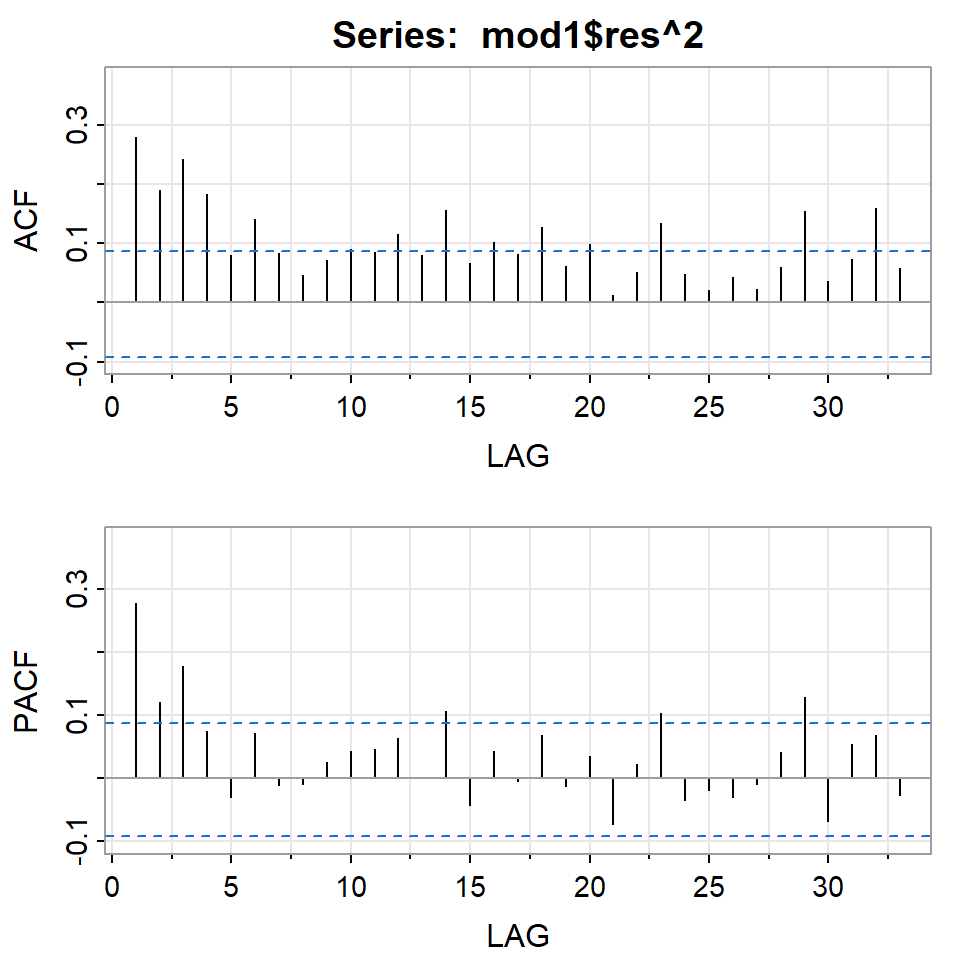
Si elevamos al cuadrado la serie simulada \(X_t\).
- Modelo ARCH(r):
\[X_t=\sqrt{h_t} \epsilon_t\] \[h_t= \alpha_0 +\alpha_1 X_{t-1}^2+\alpha_2 X_{t-2}^2+...+\alpha_r X_{t-r}^2\] en donde \(\epsilon_t\) es ruido blanco gaussiano estándar, i.e. \(\epsilon_t \sim i.i.d. N(0,1)\), y \(\alpha_0 >0\) y \(\alpha_i \geq 0,i=1,...,r\).
Simulación de ARCH(2) con \(\alpha_0=0.01\), \(\alpha_1=0.2\), \(\alpha_2=0.4\)
Si elevamos al cuadrado la serie simulada \(X_t\).
GARCH
Contenido
Introducción
ARCH
GARCH
Extensiones del modelo GARCH: EGARCH y TGARCH
Distribuciones simétricas y asimétricas
GARCH
El Modelo GARCH(1,1) es definido por:
\[X_t=\sqrt{h_t} \epsilon_t\] \[h_t= \alpha_0 + \alpha_1 X_{t-1}^2 + \beta_1 h_{t-1}\]
con \(\epsilon_t \sim i.i.d. N(0,1)\), \(\alpha_0 >0\), \(\alpha_1 \geq 0\), \(\beta_1 \geq 0\) y \(\alpha_1+\beta_1 < 1\).
Simulación de GARCH(1,1) con \(\alpha_0=0.01\), \(\alpha_1=0.2\), \(\beta_2=0.4\)
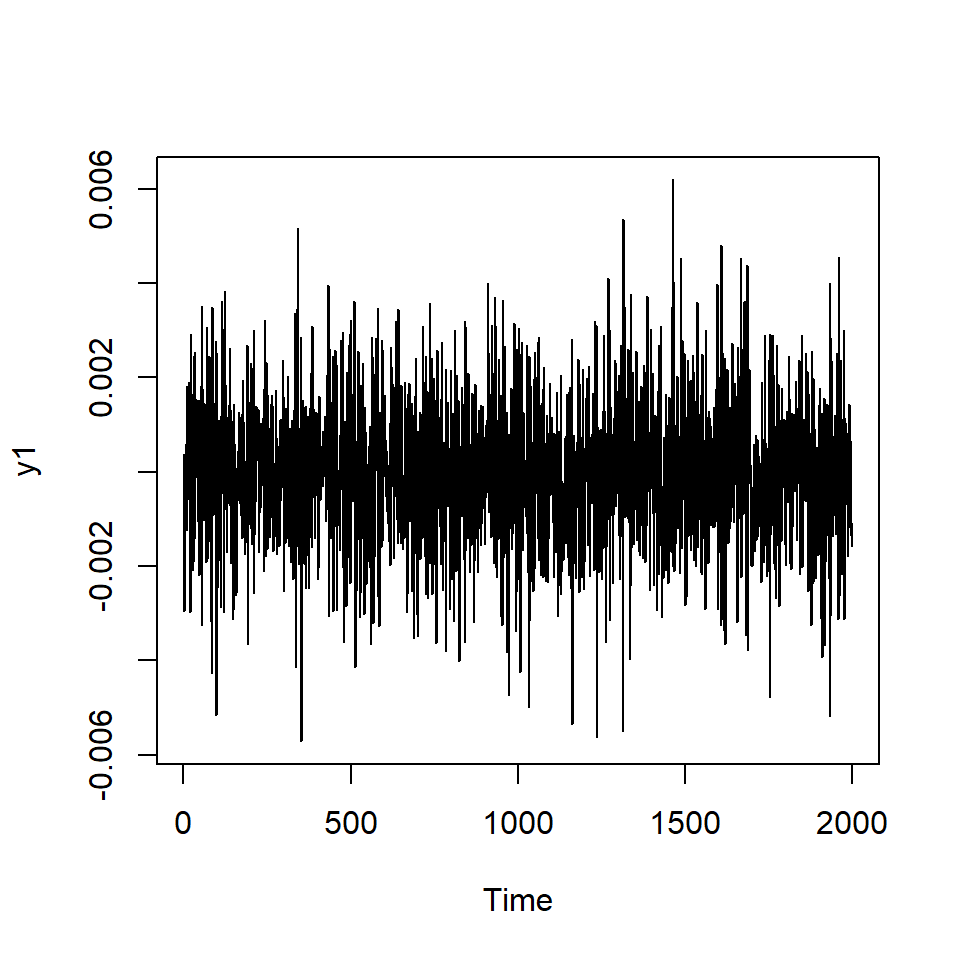
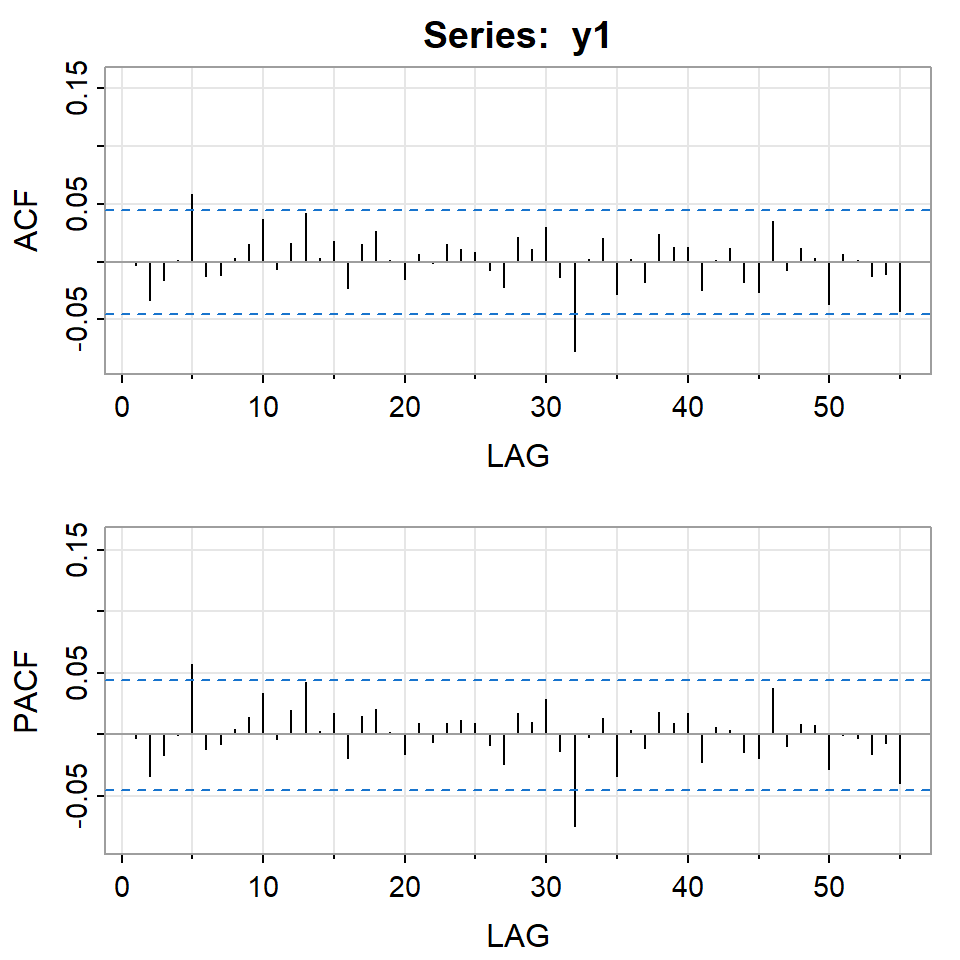
Si elevamos al cuadrado la serie simulada \(X_t\).
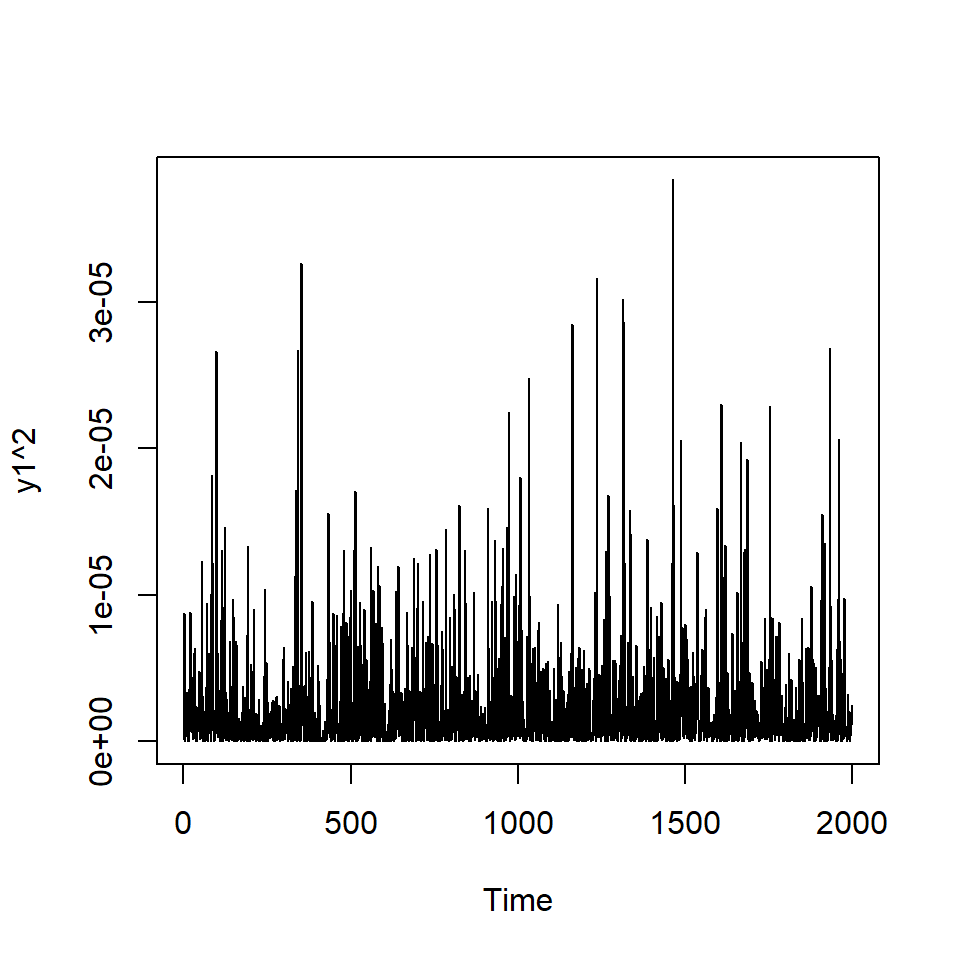
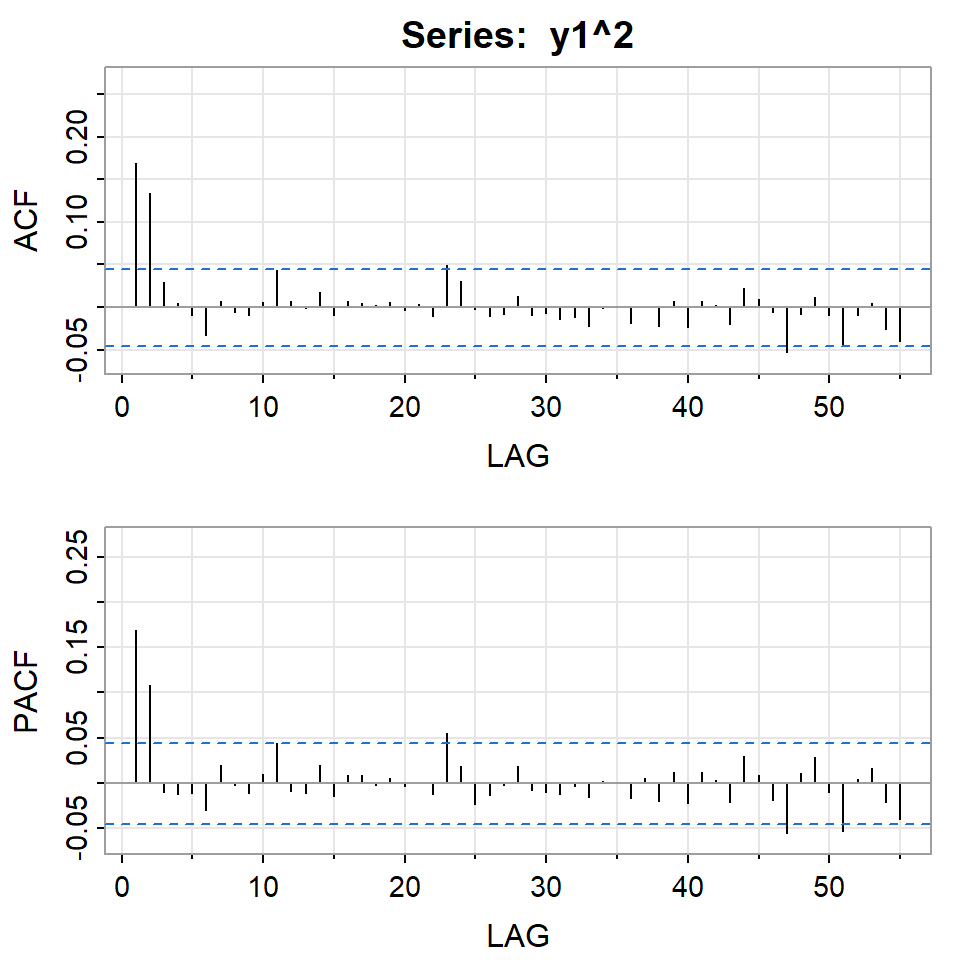
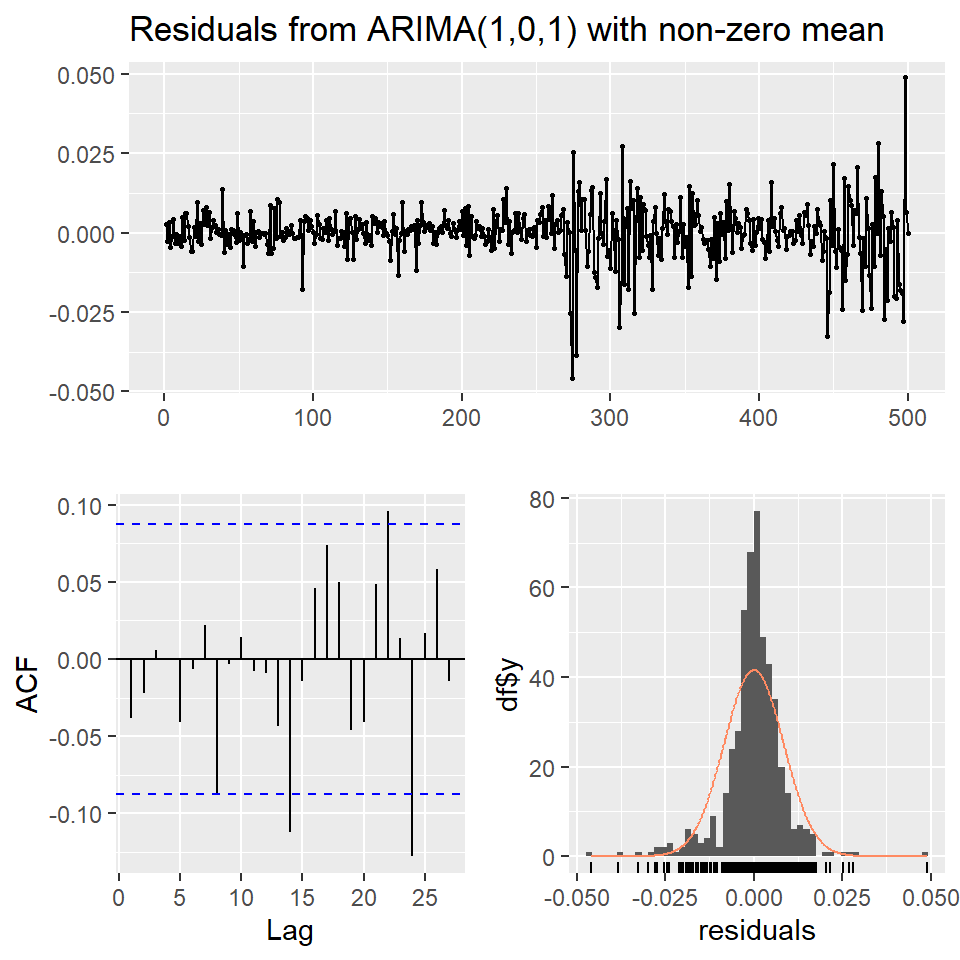
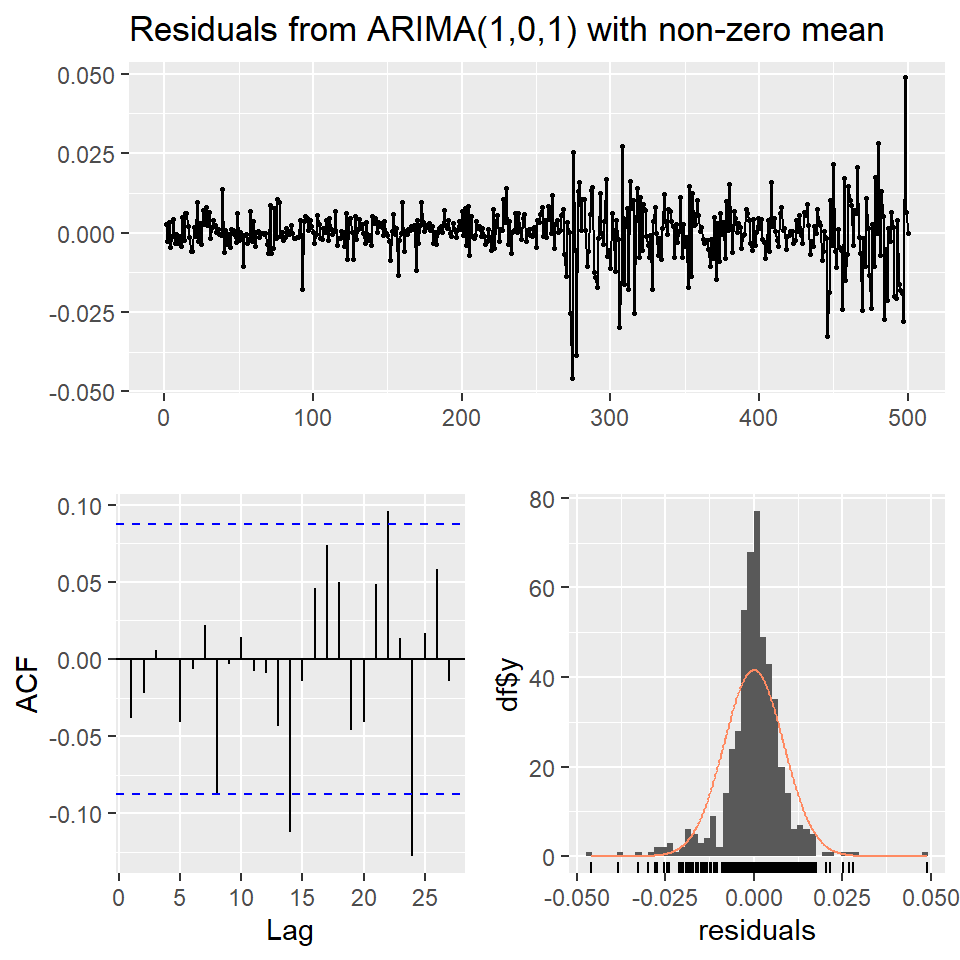
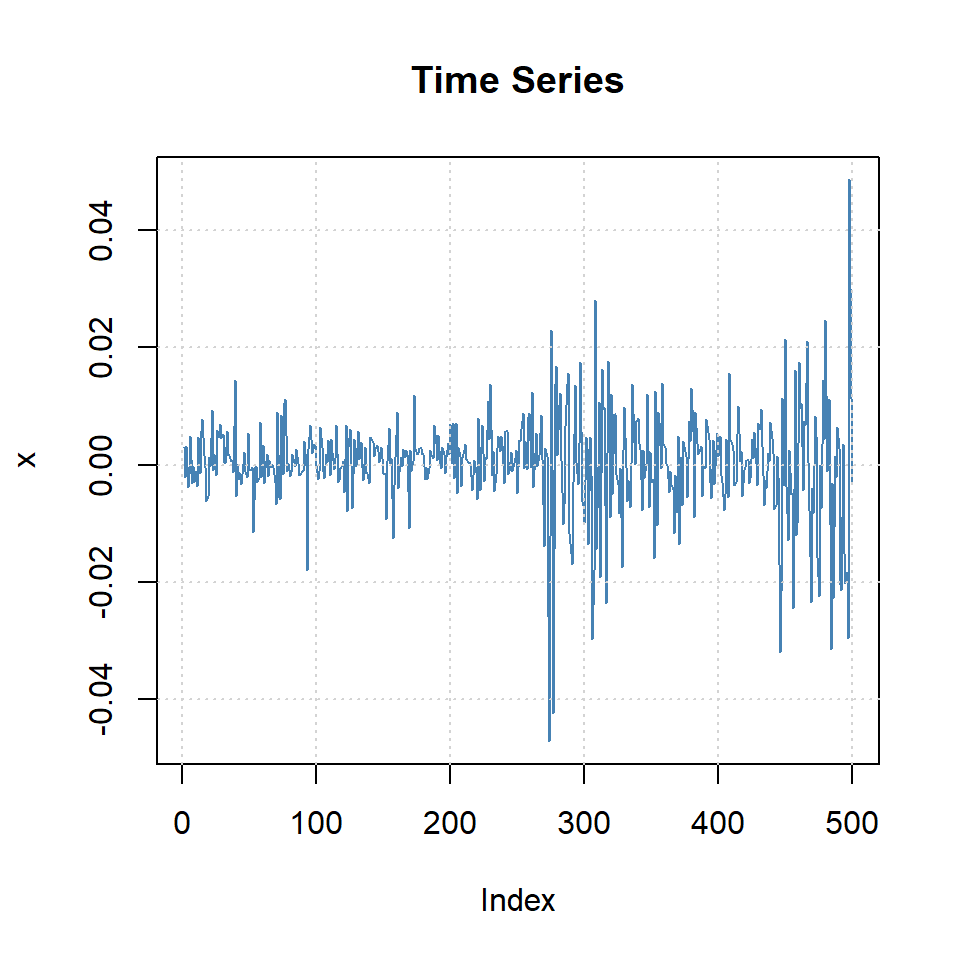
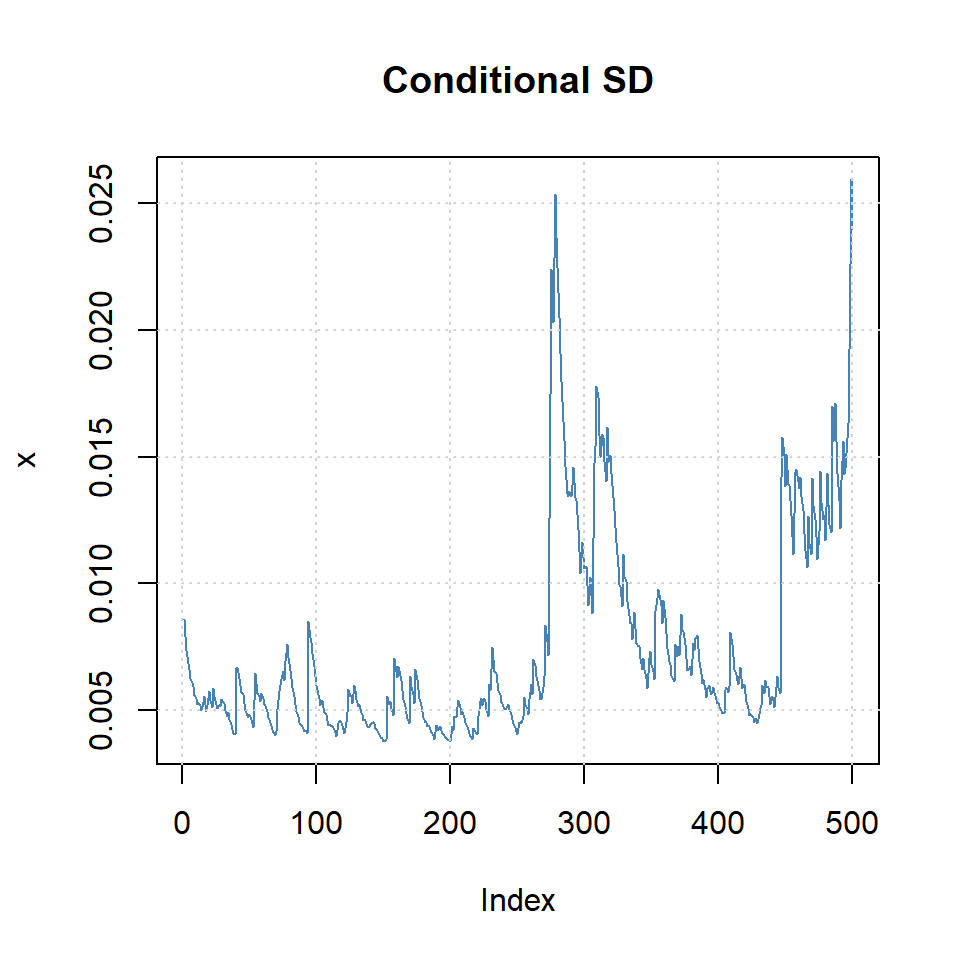
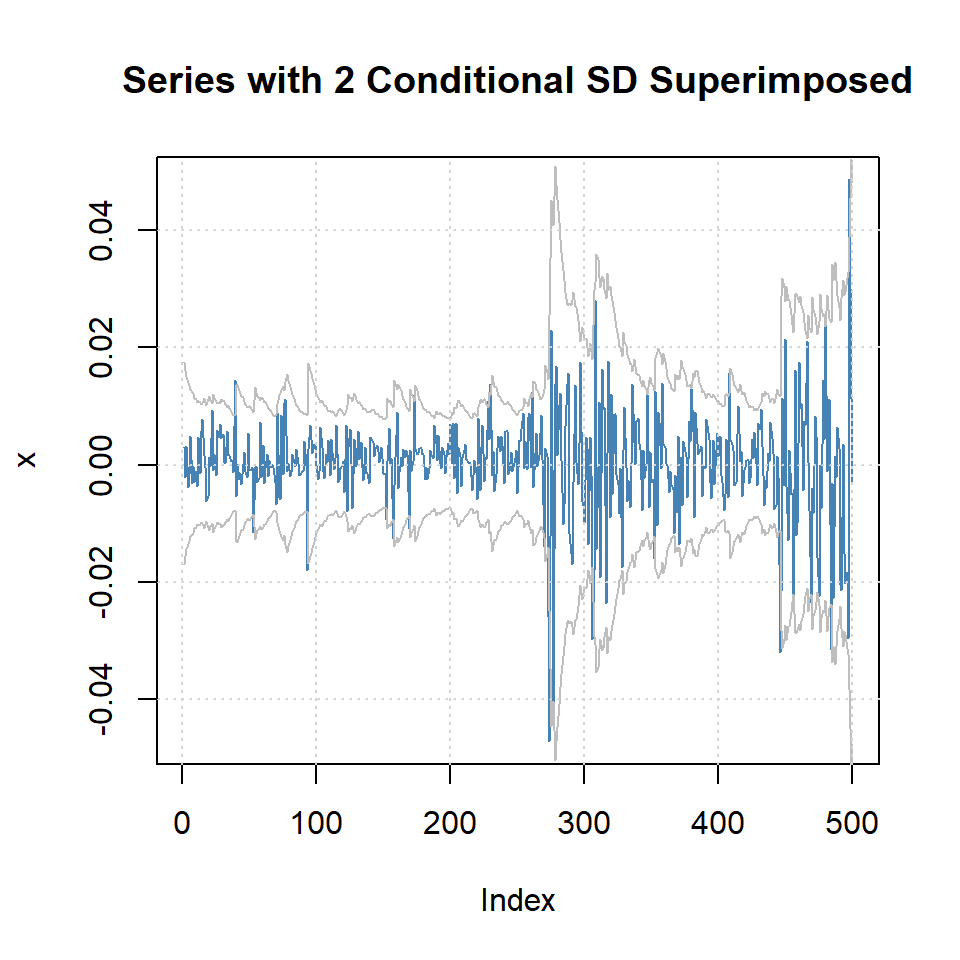
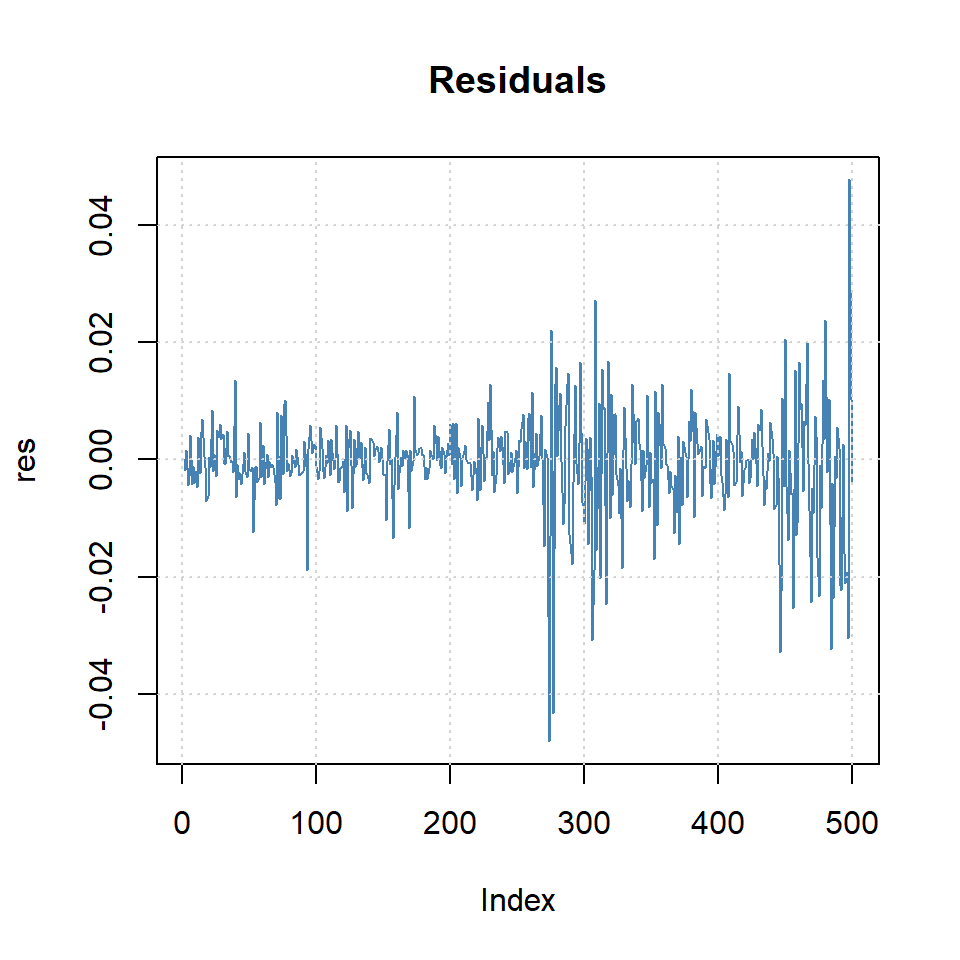
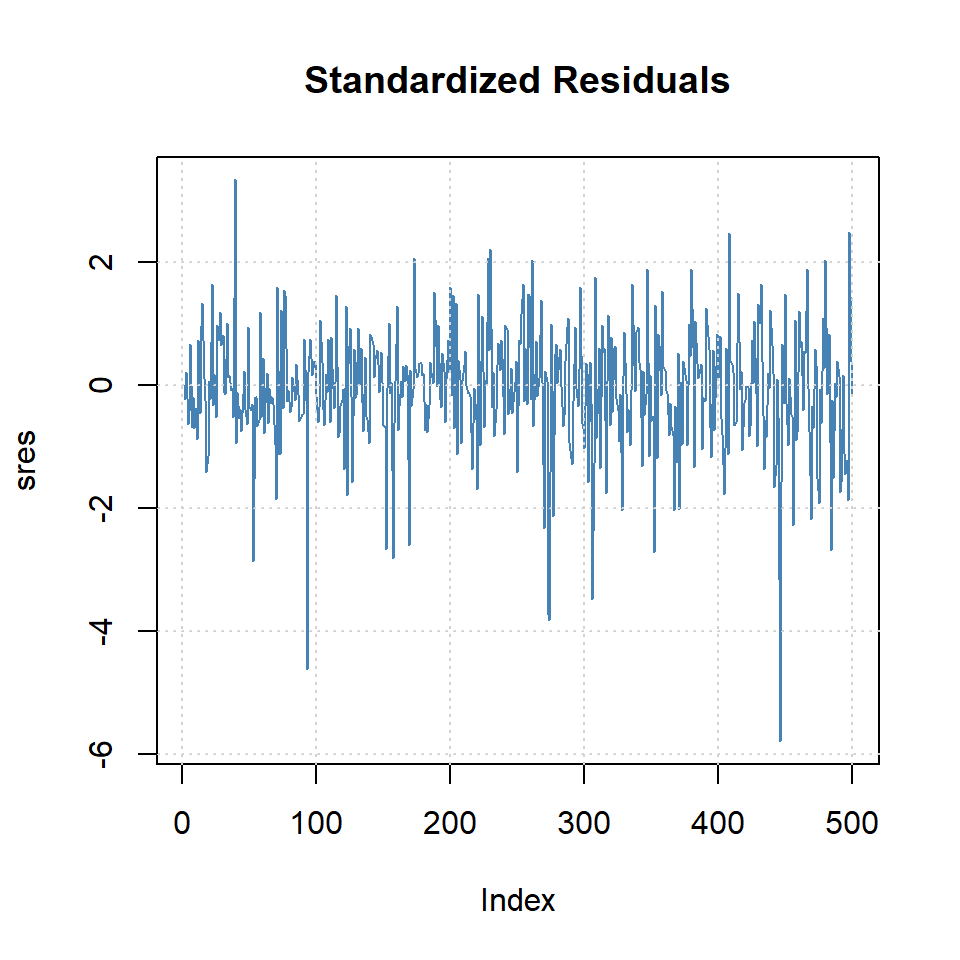
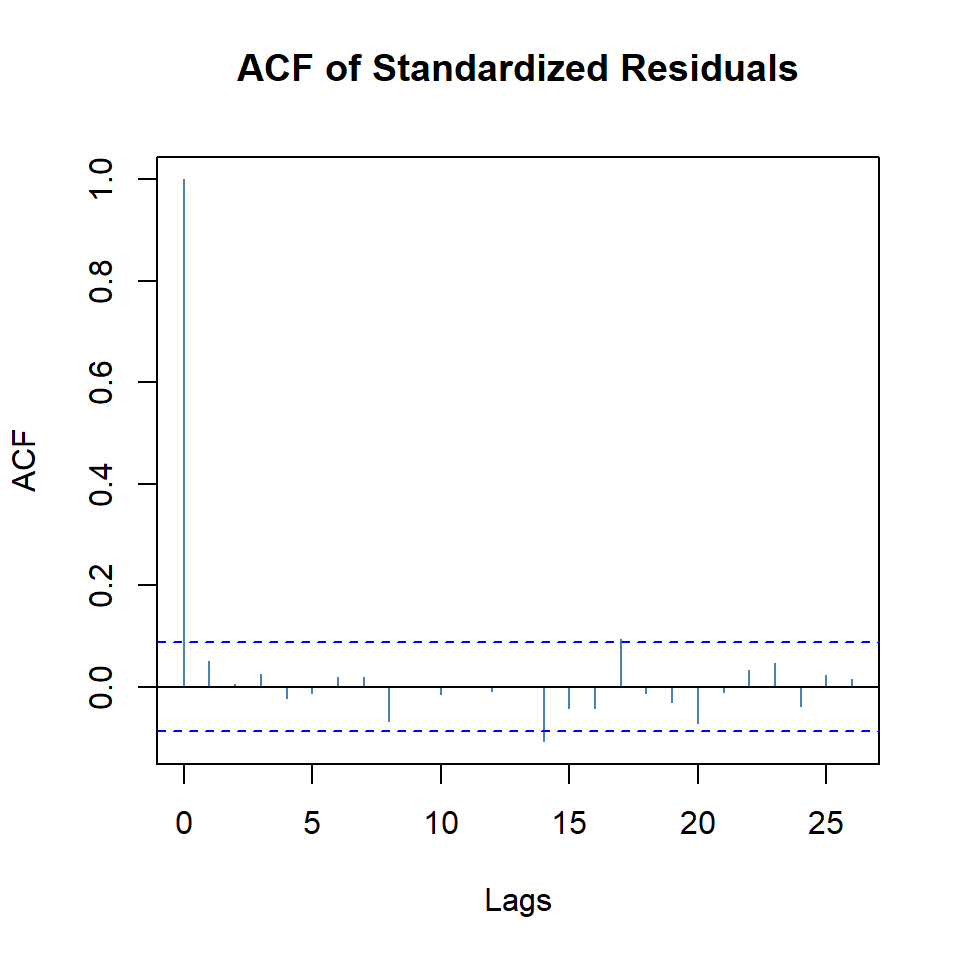
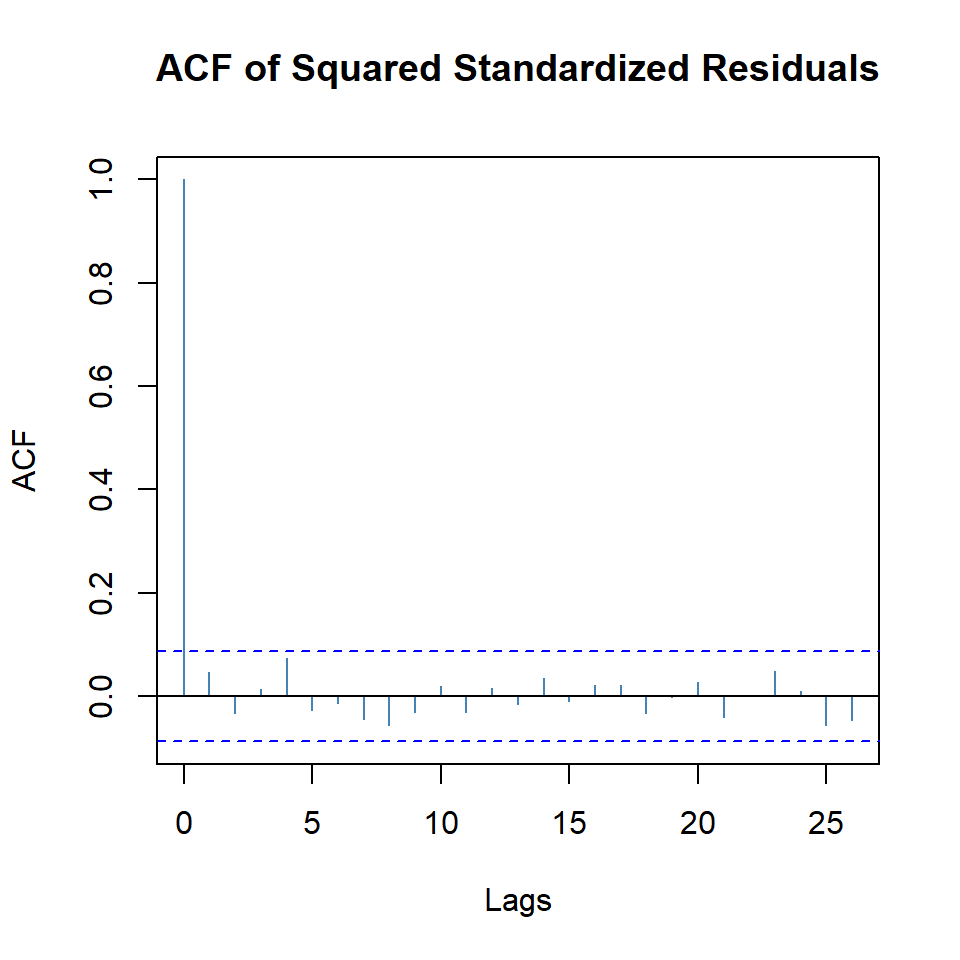
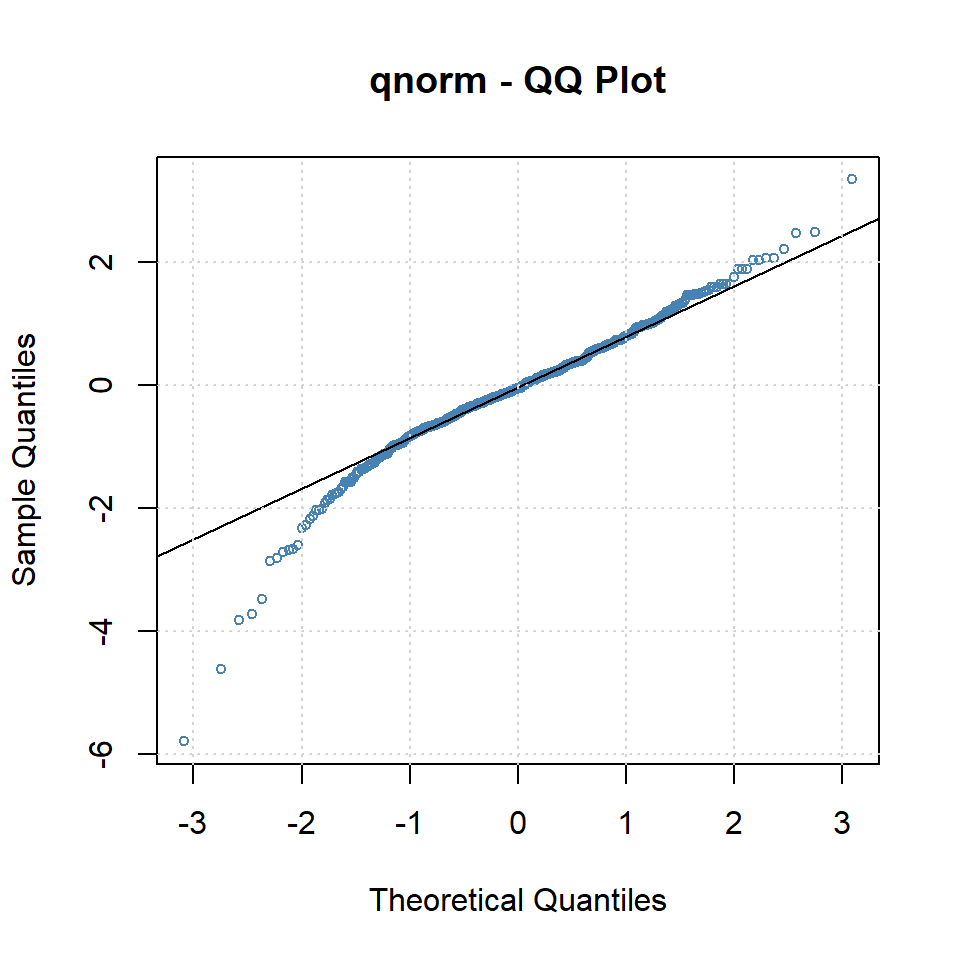
Ejemplo: promedio diario industrial Dow Jone
Series: r
ARIMA(1,0,1) with non-zero mean
Coefficients:
ar1 ma1 mean
-0.8613 0.9456 3e-04
s.e. 0.0418 0.0259 4e-04
sigma^2 = 7.121e-05: log likelihood = 1679.38
AIC=-3350.76 AICc=-3350.68 BIC=-3333.9
Training set error measures:
ME RMSE MAE MPE MAPE MASE
Training set 1.210921e-05 0.008413378 0.005502822 98.24685 154.1698 0.7121837
ACF1
Training set -0.03847749 Estimate Std. Error t value Pr(>|t|)
mu 1.500179e-03 6.579730e-04 2.280001 2.260763e-02
ar1 -5.868758e-01 5.305396e-01 -1.106187 2.686458e-01
ma1 5.889133e-01 5.449086e-01 1.080756 2.798056e-01
omega 1.737066e-06 7.635410e-07 2.275013 2.290513e-02
alpha1 1.598314e-01 4.003845e-02 3.991948 6.553261e-05
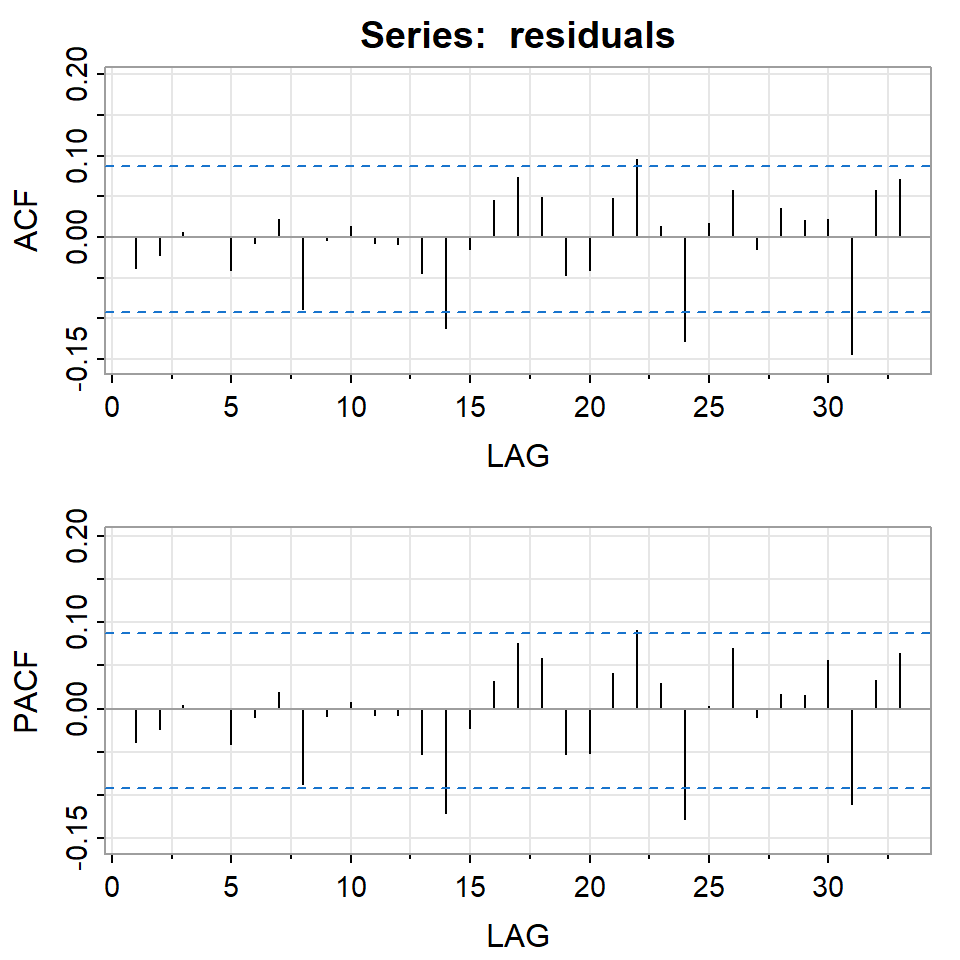
beta1 8.280899e-01 4.305972e-02 19.231194 0.000000e+00El Modelo ARMA(1,1)+GARCH(1,1):
\[r_t= 0.0015 -0.59 r_{t-1} + \varepsilon_t + 0.59 \varepsilon_{t-1}\] \[\varepsilon_t=\sqrt{h_t} \epsilon_t\] \[h_t= 0.0000017 + 0.16 \varepsilon_{t-1}^2 + 0.83 h_{t-1}\]
- Los coeficientes de la parte de ARMA no son significativos.
Estimate Std. Error t value Pr(>|t|)
mu 0.0015 0.0007 2.2800 0.0226
ar1 -0.5869 0.5305 -1.1062 0.2686
ma1 0.5889 0.5449 1.0808 0.2798
omega 0.0000 0.0000 2.2750 0.0229
alpha1 0.1598 0.0400 3.9919 0.0001
beta1 0.8281 0.0431 19.2312 0.0000- Lo ideal es eliminarlos del modelo.
Estimate Std. Error t value Pr(>|t|)
mu 0.0010 0.0003 3.6563 0.0003
omega 0.0000 0.0000 2.2971 0.0216
alpha1 0.1594 0.0397 4.0151 0.0001
beta1 0.8285 0.0426 19.4699 0.0000GARCH
El Modelo GARCH(r,s) es definido por:
\[X_t=\sqrt{h_t} \epsilon_t\] \[h_t= \alpha_0 + \sum_{i=1}^r \alpha_i X_{t-i}^2 + \sum_{j=1}^s \beta_j h_{t-j}\] \[= \alpha_0 +\alpha_1 X_{t-1}^2+\alpha_2 X_{t-2}^2+...+\alpha_r X_{t-r}^2\] \[+\beta_1 h_{t-1}+...+\beta_s h_{t-s}\] en donde \(\epsilon_t \sim i.i.d. N(0,1)\), \(\alpha_0 >0\), \(\alpha_i \geq 0\), \(\beta_j \geq 0\) y \(\sum\limits_{i=1}^q (\alpha_i+\beta_i) < 1, q=max(r,s)\).
Extensiones del modelo GARCH: EGARCH y TGARCH
Contenido
Introducción
ARCH
GARCH
Extensiones del modelo GARCH: EGARCH y TGARCH
Distribuciones simétricas y asimétricas
Extensiones del modelo GARCH
Son modelos heteroscedásticos condicionales que tratan a la asimetría de la serie.
- Exponential GAGRCH (EGARCH).
- Threshold GARCH (TGARCH).
Ejemplo: promedio diario industrial Dow Jone
Exponential GAGRCH (EGARCH)
- Esta clase de modelo, propuesto por Nelson (1991), permite el efecto de asimetría entre los retornos positivos y negativos.
\[X_t=\sqrt{h_t} \epsilon_t\] \[\ln (h_t)= \alpha_0 + \alpha_1 g(\epsilon_{t-1}) + \beta_1 \ln (h_{t-1})\] donde \(\epsilon_t\) son i.i.d. con media zero y \(g(\cdot)\) es llamada la curva de impacto de información dada por: \[g(\epsilon_t)=\theta \epsilon_t + \gamma \left[ |\epsilon_t|-E(|\epsilon_t|) \right]\] y \(\theta\) y \(\gamma\) son parámetros reales.
- Note que \(|\epsilon_t|-E(|\epsilon_t|)\) es una secuencia de variables i.i.d. con media cero.
- Y por lo tanto, \(E[g(\epsilon_t)]=0\)
- Si se abre la expresión, se tiene que:
\[g(\epsilon_t)=\left\lbrace \begin{aligned} (\theta + \gamma) \epsilon_t - \gamma E(|\epsilon_t|) & & \text{si}~ \epsilon_t \geq 0 \\ (\theta - \gamma) \epsilon_t - \gamma E(|\epsilon_t|) & & \text{si}~ \epsilon_t < 0 \end{aligned} \right.\]
De esta forma, esperamos que los retornos negativos tengan más impacto en la volatilidad, cuando \(\gamma<0\).
Esta asimetría permite que la volatilidad responde más rápidamente a retornos negativos que los positivos.
De forma general, un EGARCH(m,n) es:
\[X_t=\sqrt{h_t} \epsilon_t\] \[\ln (h_t)= \alpha_0 + \frac{1+\beta_1 B + ...+ \beta_{n-1} B^{n-1}}{1-\alpha_1 B - ...- \alpha_m B^m} g(\epsilon_{t-1})\] donde los operadores en \(B\) tienen raíces fuera del círculo unitario.
- Como ilustración, considere un EGARCH(1,1), i.e.
\[\ln (h_t)= \alpha_0 + \frac{1}{1-\alpha_1 B} g(\epsilon_{t-1})\] \[(1-\alpha_1 B) \ln (h_t)= (1-\alpha_1) \alpha_0 + g(\epsilon_{t-1})\]
\[g(\epsilon_t)=\left\lbrace \begin{aligned} (\theta + \gamma) \epsilon_t - \gamma E(|\epsilon_t|) & & \text{si}~ \epsilon_t \geq 0 \\ (\theta - \gamma) \epsilon_t - \gamma E(|\epsilon_t|) & & \text{si}~ \epsilon_t < 0 \end{aligned} \right.\]
Threshold GAGRCH (TGARCH).
Esta clase de modelo también permite agregar un efecto de asimetría entre los retornos positivos y negativos.
Un modelo TGARCH(m,n) asume la siguiente forma:
\[X_t=\sqrt{h_t} \epsilon_t\] \[h_t= \alpha_0 + \sum_{i=1}^n (\alpha_i + \gamma_i I_{\left\lbrace X_{t-i}<0\right\rbrace }) X^2_{t-i} + \sum_{j=1}^m \beta_j h_{t-j}\] donde \(I_{\left\lbrace X_s<0\right\rbrace}\) es una función indicadora, i.e.
\[I_{\left\lbrace X_s<0\right\rbrace}= \left\lbrace \begin{aligned} 1 & & \text{si}~ X_s<0 \\ 0 & & \text{si}~ X_s>0 \\ \end{aligned} \right.\]
- Un modelo TGARCH(1,1) asume la siguiente forma:
\[X_t=\sqrt{h_t} \epsilon_t\] \[h_t= \alpha_0 + (\alpha_1 + \gamma_1 I_{\left\lbrace \epsilon_{t-1}<0\right\rbrace }) \epsilon^2_{t-1} + \beta_1 h_{t-1}\] donde \(I_{\epsilon_s>0}\) es una función indicadora, i.e.
\[I_{\left\lbrace\epsilon_s>0\right\rbrace}= \left\lbrace \begin{aligned} 1 & & \text{si}~ \epsilon_s<0~~~ \text{(mala noticia)} \\ 0 & & \text{si}~ \epsilon_s>0~~~ \text{(buena noticia)} \\ \end{aligned} \right.\]
Si \(\gamma \neq 0\), hay un impacto de información asimétrica.
Si \(\gamma > 0\), mala noticia tiene un impacto mayor.
Distribuciones simétricas y asimétricas
Contenido
Introducción
ARCH
GARCH
Extensiones del modelo GARCH: EGARCH y TGARCH
Distribuciones simétricas y asimétricas
Distribuciones simétricas y asimétricas
La mayoría de los modelos suponen distribución simétrica de las innovaciones (normal, t-student, etc.).
Si una distribución \(X\) es simétrica alrededor de cero, entonces su función de densidad satisface \[f(x)=f(-x)\]
En la práctica es común enfrentar situaciones en donde los datos presentan asimetría. Por ejemplo, más impacto en los retornos negativos que los positivos, etc.
La idea es incorporar asimetría a una distribución simétrica que ya es conocida.
Incorporación de la asimetría en una distribución simétrica
Sea \(f(x)\) la función de densidad simétrica de una variable aleatoria y \(\gamma \in (0,\infty)\).
La clase de distribuciones asimétricas generadas a partir de \(f(x)\) se define como: \[p(x|\gamma) =\frac{2}{\gamma+\frac{1}{\gamma}} \left[ f\left(\frac{x}{\gamma}\right) I_{[0,\infty)}(x) + f(\gamma x) I_{(-\infty,0]}(x) \right]\]
La idea es introducir factores de escala inversa tanto en el lado positivo como el negativo del dominio.
La moda sigue siendo cero y \(p(x|\gamma)\) es asimétrica cuando \(\gamma \neq 1\).
Entre las más conocidas son:
- normal asimétrica
- t-student asimétrica
- error generalizada asimétrica
Distribución normal asimétrica
- La función de densidad de una normal estandarizada:
\[f(x)=\frac{1}{\sqrt{2 \pi}}e^{\frac{-1}{2}x^2},~~x \in \mathbb{R}\]
x <- seq(-3,3,0.01)
norm <- dnorm(x, mean = 0, sd = 1, log = FALSE)
snorm.p <- dsnorm(x, mean = 0, sd = 1, xi = 1.5, log = FALSE)
snorm.n <- dsnorm(x, mean = 0, sd = 1, xi = 0.5, log = FALSE)
plot(x,norm,type="l",col=1,ylim=c(0,0.8))
points(x,snorm.p,type="l",col=2)
points(x,snorm.n,type="l",col=3)
legenda=c("norm",TeX(r'(snorm $\gamma = 1.5$)'),TeX(r'(snorm $\gamma = 0.5$)'))
legend("topright",legenda ,col=c(1,2,3),lty=c(1))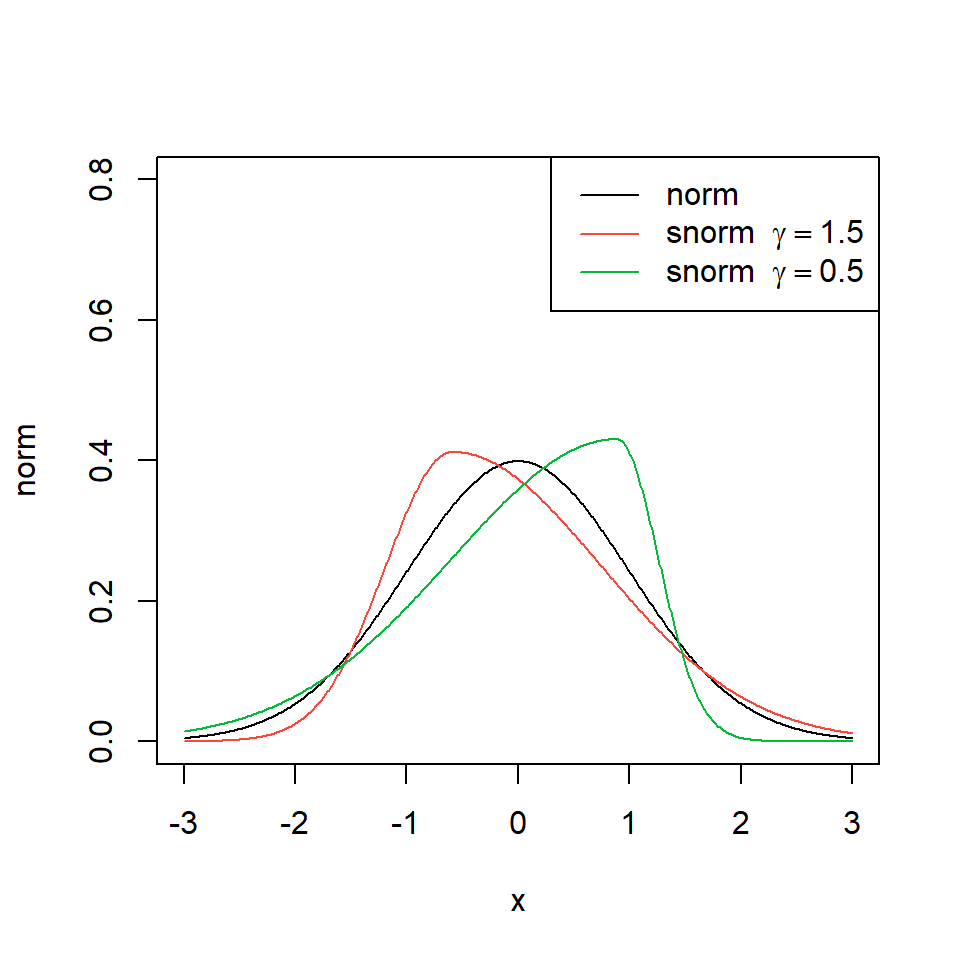
Distribución t-student asimétrica
- La función de densidad de una t-student estandarizada:
\[f(t)=\frac{\Gamma(\frac{\nu+1}{2})}{\Gamma(\sqrt{\nu \pi}\frac{\nu}{2})}\left( 1+\frac{t^2}{\nu}\right)^{-(\nu+1)/2},\]
y \(t \in \mathbb{R}\)
x <- seq(-3,3,0.01)
norm <- dnorm(x, mean = 0, sd = 1, log = FALSE)
std <- dsstd(x, mean = 0, sd = 1, nu = 4, xi = 1, log = FALSE)
sstd.p <- dsstd(x, mean = 0, sd = 1, nu = 4, xi = 1.5, log = FALSE)
sstd.n <- dsstd(x, mean = 0, sd = 1, nu = 4, xi = 0.5, log = FALSE)
plot(x,norm,type="l",col=1,ylim=c(0,1))
points(x,std,type="l",col=2)
points(x,sstd.p,type="l",col=3)
points(x,sstd.n,type="l",col=4)
legenda=c("norm",TeX(r'(st $\gamma = 1$)'),TeX(r'(st $\gamma = 1.5$)'),TeX(r'(st $\gamma = 0.5$)'))
legend("topright",legenda ,col=c(1,2,3,4),lty=c(1))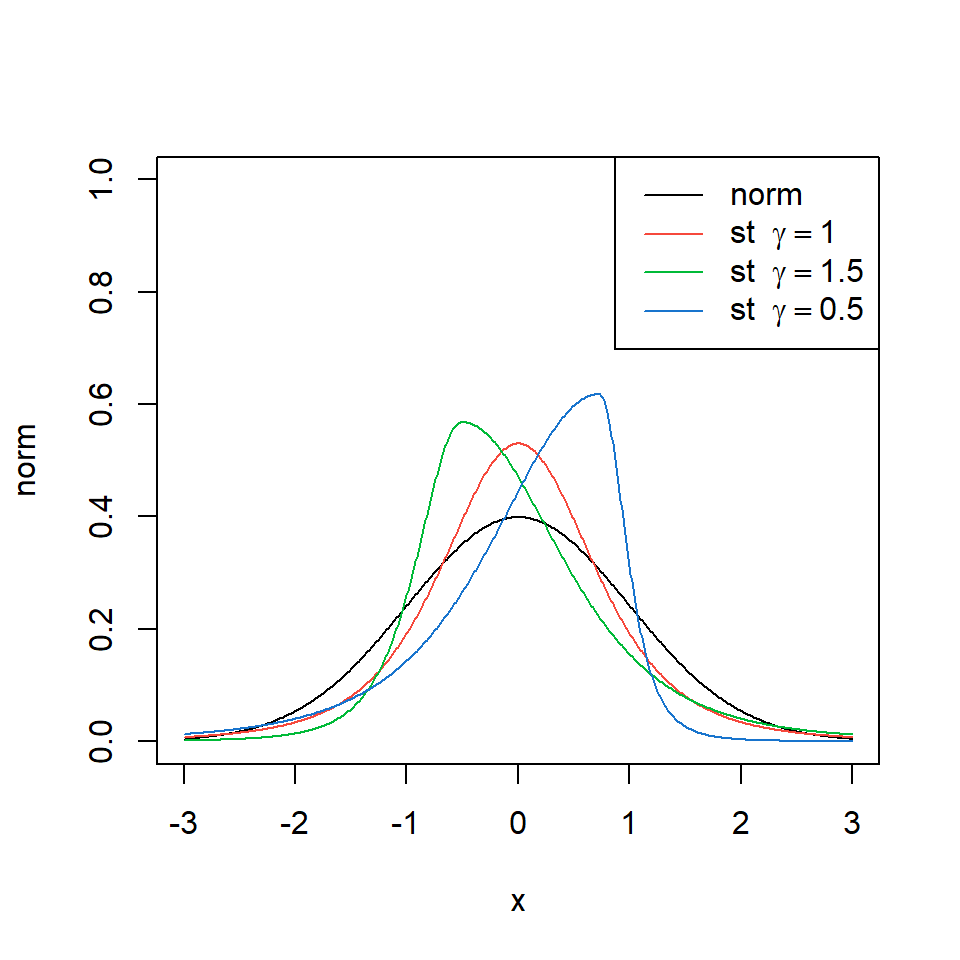
Distribución de error generalizada
- La función de densidad de una distribución de error generalizada:
\[f(x)=\frac{\beta}{2 \alpha \Gamma\left(\frac{1}{\beta}\right)}e^{\left( \frac{|x-\mu|}{\alpha}\right)^\beta}, x \in \mathbb{R}\] con parámetro de locación \(\mu \in \mathbb{R}\), escala \(\alpha >0\) y forma \(\beta >0\).
Distribución de error generalizada
- Considere una distribución de error generalizada con \(\mu=0, \alpha=1, \beta=3\) y su versión asimétrica con \(\gamma\).
x <- seq(-3,3,0.01)
norm <- dnorm(x, mean = 0, sd = 1, log = FALSE)
sged <- dsged(x, mean = 0, sd = 1, nu = 3, xi = 1, log = FALSE)
sged.p <- dsged(x, mean = 0, sd = 1, nu = 3, xi = 1.5, log = FALSE)
sged.n <- dsged(x, mean = 0, sd = 1, nu = 3, xi = 0.5, log = FALSE)
plot(x,norm,type="l",col=1,ylim=c(0,0.6))
points(x,sged,type="l",col=2)
points(x,sged.p,type="l",col=3)
points(x,sged.n,type="l",col=4)
legenda=c("norm",TeX(r'(sged $\gamma = 1$)'),TeX(r'(sged $\gamma = 1.5$)'),TeX(r'(sged $\gamma = 0.5$)'))
legend("topright",legenda ,col=c(1,2,3,4),lty=c(1))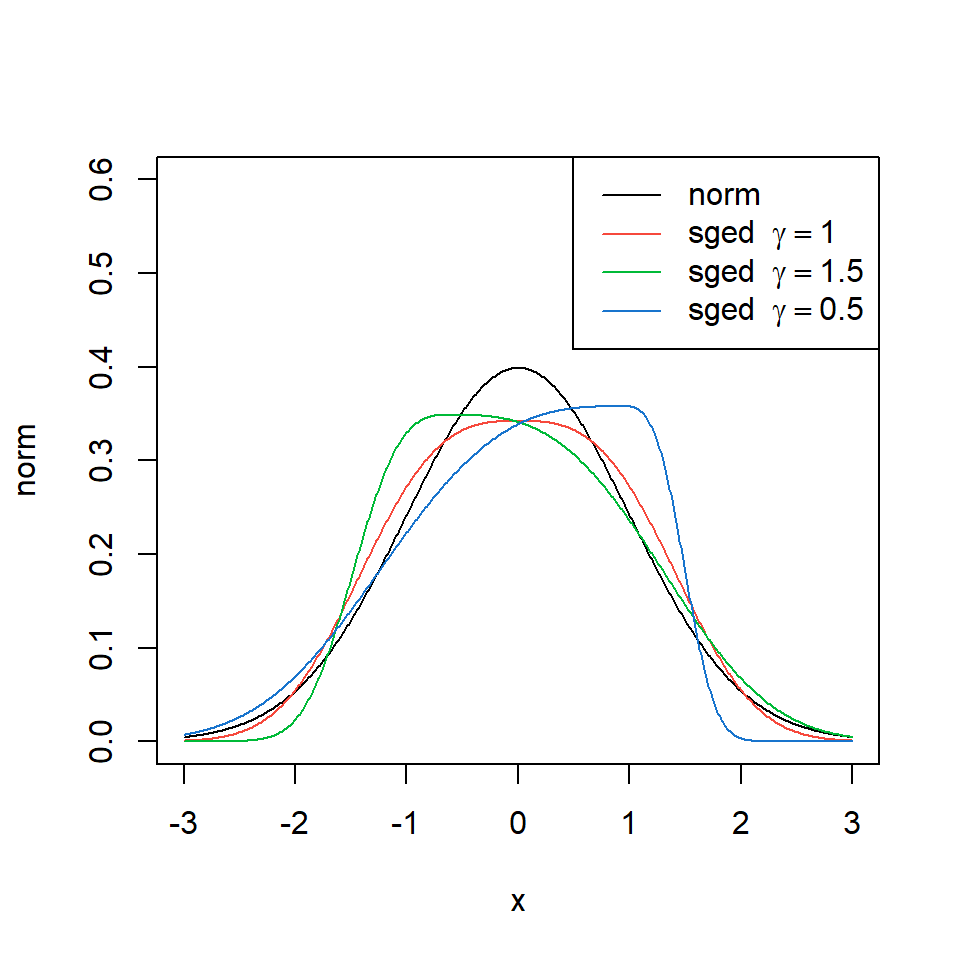
Paquetes en R
Para replicar los ejemplos de esta presentación, necesitan estos paquetes: