XS3310 Teoría Estadística

.title[
# XS3310 Teoría Estadística
]
.subtitle[
## I Semestre 2023
]
.author[
### Escuela de Estadística
]
.date[
### 06-06-2023
]

---

# ¿Qué hemos visto hasta ahora?

Introducción a la Estadística Bayesiana: filosofía, historia y un poco de cálculo.

# ¿Qué vamos a discutir hoy?

Distribuciones previas

---

## Aclaración de parametrización

Para facilitar algunos cálculos en este tema estaremos usando una parametrización alterna de la Gamma (y por ende de la ji-cuadrado y la Exponencial). Anteriormente si teníamos una `$Gamma(\alpha,\beta)$` su función de densidad venía dada por 
	
`$$f_{X}(x) = \frac{x^{\alpha - 1} e^{-\frac{x}{\beta}}  }{\beta^{\alpha} \Gamma(\alpha) } \quad si \quad x > 0$$`
	
Con la nueva parametrización que vamos a estar utilizando, la función de densidad vendría dada de la siguiente manera

`$$f_{X}(x) = \frac{ \beta^{\alpha} x^{\alpha - 1} e^{-\beta x}  }{ \Gamma(\alpha) } \quad si \quad x > 0$$`
	
Noten que la única diferencia es que el `$\beta$` de la nueva parametrización, llamémoslo `$\beta^{\prime}$` por un momento, es el inverso multiplicativo del beta de la parametrización vieja. Es decir, `$\beta^{\prime} = \frac{1}{\beta}$`. Por lo tanto, para la nueva parametrización de la Gamma tenemos que `$E(X) = \frac{\alpha}{\beta}$` y `$Var(X) = \frac{\alpha}{\beta^2}$`.
			
			
---

## Densidades previas conjugadas y estimadores de Bayes
    
### Distribución previa (distribución a priori)

Suponga que tenemos un modelo estadístico con parámetro `$\theta$`. Su `$\theta$` es aleatorio entonces su densidad (antes de observar cualquier muestra) se llama **densidad previa**: `$\pi$`.

**Ejemplo**: `$X_1,\dots, X_n \sim \text{Exp}(\theta)$` y `$\theta$` es aleatorio tal que `$\theta \sim \Gamma(\stackrel{\alpha}{1},\stackrel{\beta}{2})$` entonces

$$ \pi(\theta) = \dfrac{1}{\Gamma(\alpha)}\beta^\alpha\theta^{\alpha-1}e^{\beta\theta} = 2e^{-2\theta}, \quad \theta > 0$$

---

**Ejemplo**: Sea `$\theta$` la probabilidad de obtener cara al tirar una moneda.

En este caso antes de modelar exactamente el `$\theta$`, lo importante es modelar el tipo de moneda. Es decir, supongamos que tenemos dos opciones

- *Moneda justa:* `$\theta = \dfrac{1}{2}$` con probabilidad previa `$0.8$` `$(\pi(\frac{1}{2}) = 0.8)$`.

- *Moneda con solo una cara:* `$\theta = 1$`  con probabilidad previa `$0.2$` `$(\pi(1) = 0.2)$`.

En este ejemplo si tuviéramos 100 monedas con probabilidad previa `$\pi$` entonces 20 tendrían solo una cara y 80 serían monedas normales.

---

**Notas**:

- `$\pi$` está definida en `$\Omega$` (espacio paramétrico).

- `$\pi$` es definida antes de obtener la muestra.

**Ejemplo** (Componentes eléctricos) Supoga que se quiere conocer el tiempo de
vida de cierto componente eléctrico. Sabemos que este tiempo se puede modelar
con una distribución exponencial con parámetro `$\theta$` desconocido.
Este parámetro asumimos que tiene una distribución previa Gamma.

Un experto en componentes eléctricos conoce mucho de su área y sabe
que el parámetro `$\theta$` tiene las siguientes características:

$$
\mathbb{E}[\theta] = 0.0002, \quad \sqrt{\text{Var}(\theta)} = 0.0001.
$$

Como sabemos que la previa  `$\pi$` es Gamma, podemos deducir lo siguiente:

$$
 \mathbb{E}[\theta] = \dfrac{\alpha}{\beta}, \text{Var}(\theta) = \dfrac{\alpha}{\beta^2}
$$

`$$\implies \begin{cases}\dfrac{\alpha}{\beta} = 2\times 10^{-4}\\\sqrt{\dfrac{\alpha}{\beta^2}} = 1 \times 10^{-4}\end{cases} \implies \beta = 20000, \alpha = 4$$`

---

**Notación**:

- `$X = (X_1,\dots, X_n)$`: vector que contiene la muestra aleatoria.

- Densidad conjunta de `$X$`: `$f_\theta(x)$`.

- Densidad de `$X$` condicional en `$\theta$`: `$f_n(x|\theta)$`.

**Supuesto**: `$X$` viene de una muestra aleatoria  si y solo si `$X$` es condicionalmente independiente dado `$\theta$`.

**Consecuencia**: `$$f_n(X|\theta) = f(X_1|\theta)\cdot f(X_2|\theta)\cdots f(X_n|\theta)$$`

**Ejemplo**

Si `$X = (X_1,\dots, X_n)$` es una muestra tal que `$X_i\sim \text{Exp}(\theta)$`,

`\begin{align*}
f_n(X|\theta) &= \begin{cases}\prod_{i=1}^n \theta e^{-\theta X_i} & \text{si } X_i>0\\
0 & \text{si no}
\end{cases}  \\
&= \begin{cases}\theta^n e^{-\theta\sum_{i=1}^n X_i} & X_i > 0  \\ 0 & \text{si no}\end{cases}
\end{align*}`

---
## Densidad posterior

**Definición**. Considere un modelo estadístico con parámetro `$\theta$` y muestra
aleatoria `$X_1,\dots, X_n$`. La densidad condicional de `$\theta$` dado
`$X_1,\dots,X_n$` se llama *densidad posterior*: `$\pi(\theta|X)$`

**Teorema**. Bajo las condiciones anteriores:

$$
\pi(\theta|X) =
\dfrac{f(X_1|\theta)\cdots f(X_n|\theta)\pi(\theta)}{g_n(X)} 
$$

para `$\theta \in \Omega$`, donde `$g_n$` es una constante de
normalización.

*Prueba*:

`\begin{align*}
\pi(\theta|X) & = \dfrac{\pi(\theta,X)}{\text{marginal de X}} = \dfrac{\pi(\theta,X)}{\int \pi(\theta,X)\;d\theta}= \dfrac{P(X|\theta)\cdot \pi(\theta)}{\int \pi(\theta,X)\;d\theta}\\
& \dfrac{f_n(X|\theta)\cdot \pi(\theta)}{g_n(X)} = \dfrac{f(X_1|\theta)\cdots f(X_n|\theta)\pi(\theta)}{g_n(X)}
\end{align*}`

Del ejemplo anterior,

`$$f_n(X|\theta) = \theta^n e^{-\theta y}, y = \sum{X_i} \text{ (estadístico})$$`

---

- Numerador:

`$$f_n(X|\theta)\pi(\theta) = \underbrace{\theta^n e^{-\theta y}}_{f_n(X|\theta)} \cdot \underbrace{\dfrac{200000^4}{3!}\theta^3e^{-20000\cdot\theta}}_{\pi(\theta)} = \dfrac{20000^4}{3!}\theta^{n+3}e^{(20000+y)\theta}$$`

- Denominador:

`$$g_n(x) = \int_{0}^{+\infty}\theta^{n+3}e^{-(20000+y)\theta}\;d\theta = \dfrac{\Gamma(n+4)}{(20000+y)^{n+4}}$$`

Entonces la posterior corresponde a
`$$\pi(\theta|X) = \dfrac{\theta^{n+3}e^{-(20000+y)\theta}}{\Gamma(n+4)} (20000+y)^{n+4}$$`
que es una `$\Gamma(n+4,20000+y)$`.

Con 5 observaciones (horas): 2911, 3403, 3237, 3509, 3118.
`$$y = \sum_{i=1}^{5}X_i = 16178, \quad n= 5$$`
por lo que `$\theta|X \sim \Gamma(9,36178)$`

---

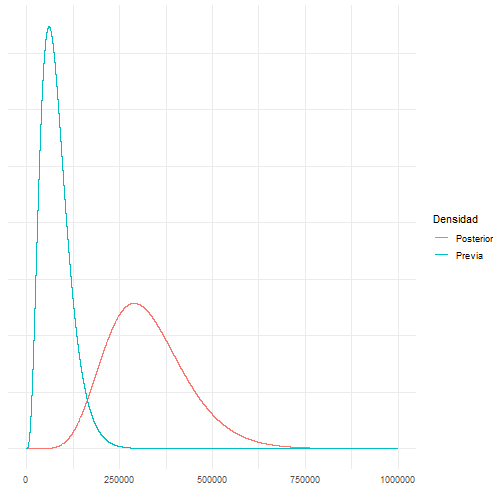
Es sensible al tamaño de la muestra (una muestra grande implica un efecto de la previa menor).

**Hiperparámetros**: parámetros de la previa o posterior.

---
## Proceso de modelación de parámetros.

De ahora en adelante vamos a entender un modelo como el conjunto de los datos `$X_1, \ldots, X_n,$` la función de densidad `$f$` y el parámetro de la densidad
`$\theta$`. Estos dos últimos resumen el comportamiento de los datos.

Ahora para identificar este modelo se hace por partes,

1. La información previa `$\pi(\theta)$` es la información extra o basado en la
   experiencia que tengo del modelo. 
2. Los datos es la información observada. La función de densidad `$f$` filtra y
   mejora la información de la previa. 
3. La densidad posterior es la "mezcla" entre la información y los datos
   observados. Es una versión más informada de la distribución del parámetro.

---
## Función de verosimilitud

Bajo el modelo estadístico anterior a `$f_n(X|\theta)$` se le llama **verosimilitud** o **función de verosimilitud**.

**Observación**. En el caso de una función de verosimilitud, el argumento es `$\theta$`.

**Ejemplo**.

Sea `$\theta$` la proporción de aparatos defectuosos, con `$\theta \in [0,1]$`

`$$X_i = \begin{cases}0 & \text{falló} \\ 1 & \text{no falló} \end{cases}$$`

`$\{X_i\}_{i=1}^n$` es una muestra aleatoria y `$X_i \sim Ber(\theta)$`.

- **Verosimilitud**

`$$f_n(X|\theta) = \prod_{i=1}^n f(X_i|\theta) = \begin{cases}\theta^{\sum X_i}(1-\theta)^{n-\sum X_i} & X_i = 0,1~ \forall i \\ 0 & \text{si no}\end{cases}$$`
---

- **Previa**:
`$$\pi(\theta) = 1_{\{0\leq\theta\leq 1\}}$$`

- **Posterior**:

Por el teorema de Bayes,
`\begin{align*}
\pi(\theta|X) \propto \theta^y (1-\theta)^{n-y}\cdot 1  \\
&= \theta^{\overbrace{y+1}^{\alpha}-1}(1-\theta)^{\overbrace{n-y+1}^{\beta}-1}
&\implies \theta|X \sim \text{Beta}(y+1,n-y+1)
\end{align*}`

- **Predicción**.

*Supuesto*: los datos son secuenciales. Calculamos la distribución posterior
secuencialmente:

`\begin{align}
\pi(\theta|X_1) & \propto \pi(\theta) f(X_1|\theta)\\
\pi(\theta|X_1,X_2) &\propto \pi(\theta) f(X_1,X_2|\theta) \\
&= \pi(\theta) f(X_1|\theta) f(X_2|\theta) \text{ (por independencia condicional)}
\\ & = \pi(\theta|X_1)f(X_2|\theta)\\
\vdots &  \\
\pi(\theta|X_1,\dots,X_n) & \propto f(X_n|\theta)\pi(\theta|X_1,\dots, X_{n-1})
\end{align}`

Bajo independencia condicional no hay diferencia en la posterior si los datos son secuenciales.

---
Luego,

`$$\begin{align} g_n(X) & = \int_{\Omega} f(X_n|\theta) \pi(\theta|X_1,\dots, X_{n-1})~d\theta \\ & = P(X_n|X_1,\dots,X_{n-1}) \text{ (Predicción para }X_n) \end{align}$$`
**Ejemplo**.

Continuando con el ejemplo de los artefactos, `$P(X_6>3000|X_1,X_2,X_3,X_4,X_5)$`.
Se necesita calcular `$f(X_6|X)$`. Dado que 
`$$\pi(\theta|X) = 2.6\times 10^{36}\theta^8 e^{-36178\theta}$$`

se tiene

`$$f(X_6|X) = 2.6 \times 10^{36} \int_{0}^\infty \underbrace{\theta e^{-\theta X_6}}_{\text{Densidad de } X_6} \theta^8 e^{-36178\theta}~d\theta= \dfrac{9.55 \times 10^{41}}{(X_6+36178)^{10}}$$`

Entonces,

`$$P(X_6>3000)=\int_{3000}^{\infty} \dfrac{9.55\times10^{41}}{(X_6+36178)^{10}}\; dX_6 =
0.4882$$`

---

```r
func<-function(x){9.55*10^41/(x+36178)^10}
integrate(func,lower=3000,upper=Inf)
```

```
## 0.4879558 with absolute error < 1.5e-05
```

La vida mediana se calcula como `$\dfrac{1}{2} = P(X_6>u|X)$`.

La vida media se calcula como `$E(X_6|X) = \int_{0}^{\infty} x_6 f(x_6|X) dx_6$`.

```r
func<-function(x){x*9.55*10^41/(x+36178)^10}
integrate(func,lower=0,upper=Inf)
```

```
## 4519.75 with absolute error < 0.41
```

---

## ¿Qué discutimos hoy?

Estadística Bayesiana, Distribuciones previas (a priori).

## ¿Qué nos falta para terminar el curso?

Tipos de distribuciones previas, estadística Bayesiana: inferencia (estimación puntual, intervalos de credibilidad y factor de Bayes).