lab02: Ilustración de EMV para muestras grandes

XS3310 Teoría Estadística

Autor/a

Afiliación

Shu Wei Chou Chen

Escuela de Estadística (UCR)

Este documento ilustra de manera intuitiva, por medio de simulaciones, las propiedades del EMV para muestras grandes.

1 EMV de \(\bar{X}\) y \(\bar{X}^{-1}\) de la Distribución Exponencial

Suponga que \(X_1,...,X_n\) una muestra aleatoria tal que \(X_i \sim Exp(\beta=0.5)\), para \(i=1,...,n\).

K <- 1000
n <- 20
X <- list()
for(i in 1:K){
  X[[i]] <- rexp(n,2) #X es una lista de las K muestras de tamaño 20.
}

1.1 Comportamiento de la media muestral

media_X <- sapply(X,mean)
hist(media_X)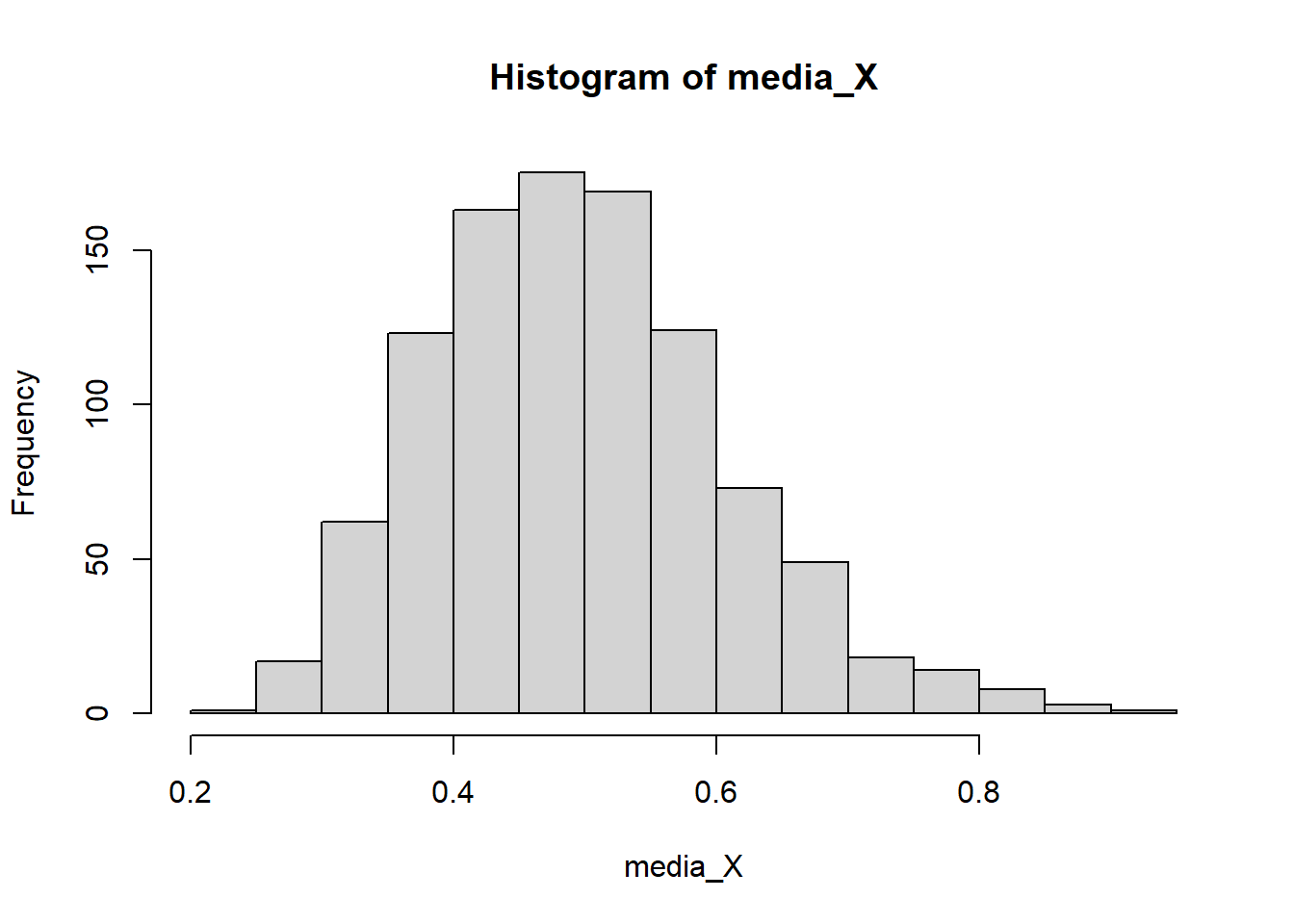

mean(media_X)

[1] 0.5033976

var(media_X)

[1] 0.01318611

Observe que teóricamente \(E(\bar{X})=0.5\) y \(Var(\bar{X})=\frac{\beta^2}{n}=\frac{0.5^2}{20}=0.0125\). El TLC nos garantiza que \[Z=\frac{\bar{X}-\mu}{\sigma/\sqrt{n}} \overset{d}{\rightarrow} N(0,1).\] Es decir, \(Z\) se aproxima cada vez a la normal estándar cuando \(n\rightarrow \infty\). Por ejemplo, con solo \(n=20\), tenemos

Z=(media_X-0.5)/(sqrt(0.5^2/n))
hist(Z,prob=TRUE,ylim=c(0,0.5))
Z2 <- seq(min(Z), max(Z), length = 40)
lines(Z2, dnorm(Z2, mean = 0, sd = 1), col = 2, lwd = 2)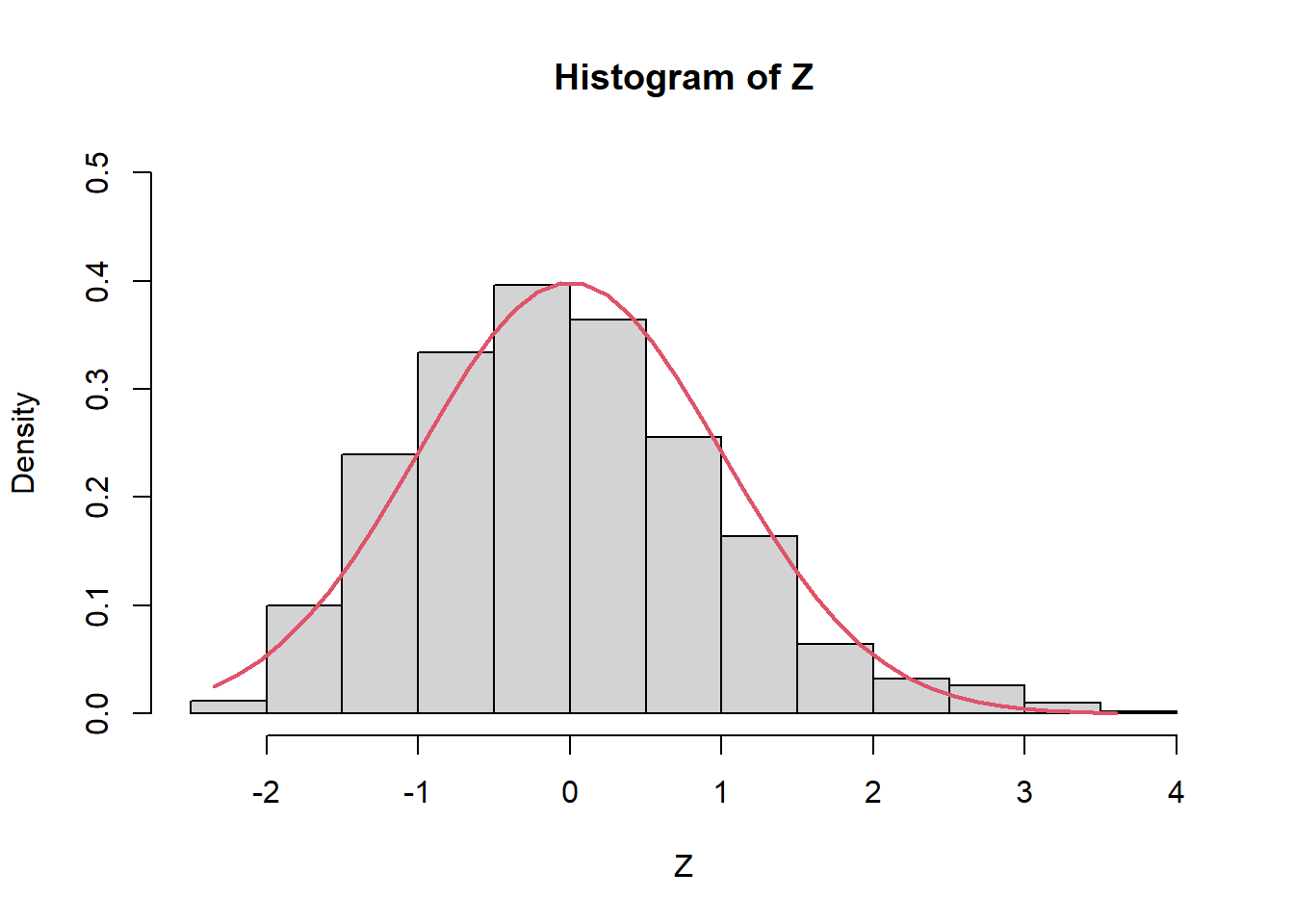

mean(Z)

[1] 0.03038933

var(Z)

[1] 1.054889

De la misma forma, puedo calcular

\[ Z_a=n^{\frac{1}{2}}(\bar{X}-\mu) \overset{d}{\rightarrow} N(0,\sigma^2) \]

Recuerde que para la distribución exponencial, \(\sigma=\beta\).

Za=sqrt(n)*(media_X-0.5)
hist(Za,prob=TRUE,ylim=c(0,1.2))
Z2 <- seq(min(Za), max(Za), length = 40)
lines(Z2, dnorm(Z2, mean = 0, sd = 0.5), col = 2, lwd = 2)

mean(Za)

[1] 0.01519466

var(Za)

[1] 0.2637222

1.2 Comportamiento de \(\bar{X}^{-1}\)

inv_media_X <- 1/media_X
head(cbind(media_X,inv_media_X))

       media_X inv_media_X
[1,] 0.5140669    1.945272
[2,] 0.4616077    2.166342
[3,] 0.3649744    2.739918
[4,] 0.5166785    1.935440
[5,] 0.4818535    2.075319
[6,] 0.4606296    2.170942

hist(inv_media_X)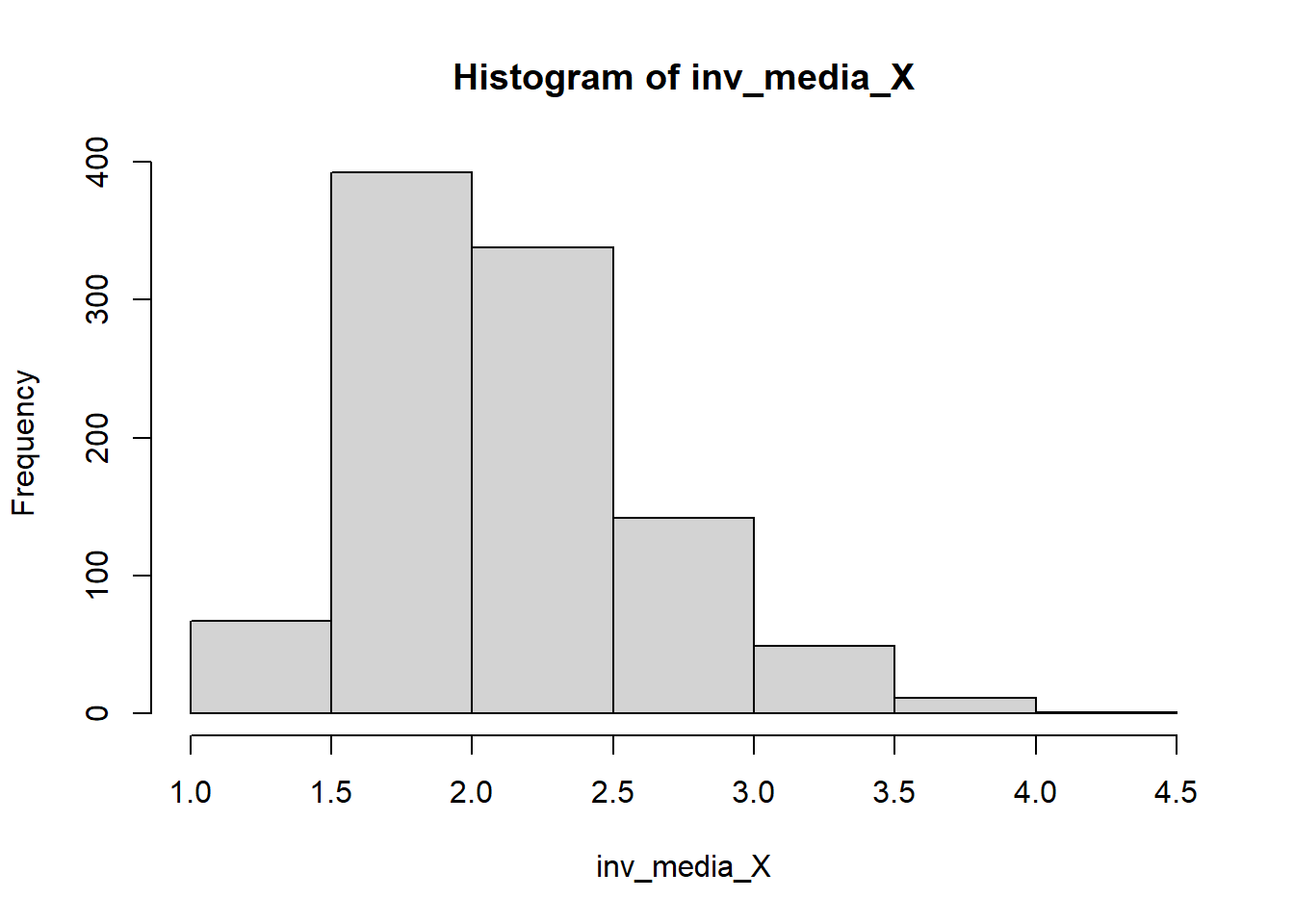

mean(media_X)

[1] 0.5033976

var(media_X)

[1] 0.01318611

Usando el resultado con el Método Delta (diapositiva 11 de la clase 8).

\[ \sqrt{n}\bigg[\dfrac{1}{\overline{X}_n}-\dfrac 1\mu\bigg]\xrightarrow{d}N\left(0,\dfrac{\sigma ^2}{\mu ^4}\right) \]

Za=sqrt(n)*(inv_media_X-(1/0.5))
hist(Za,prob=TRUE,ylim=c(0,0.25))
Z2 <- seq(min(Za), max(Za), length = 40)
lines(Z2, dnorm(Z2, mean = 0, sd = sqrt(0.5^2/0.5^4)), col = 2, lwd = 2)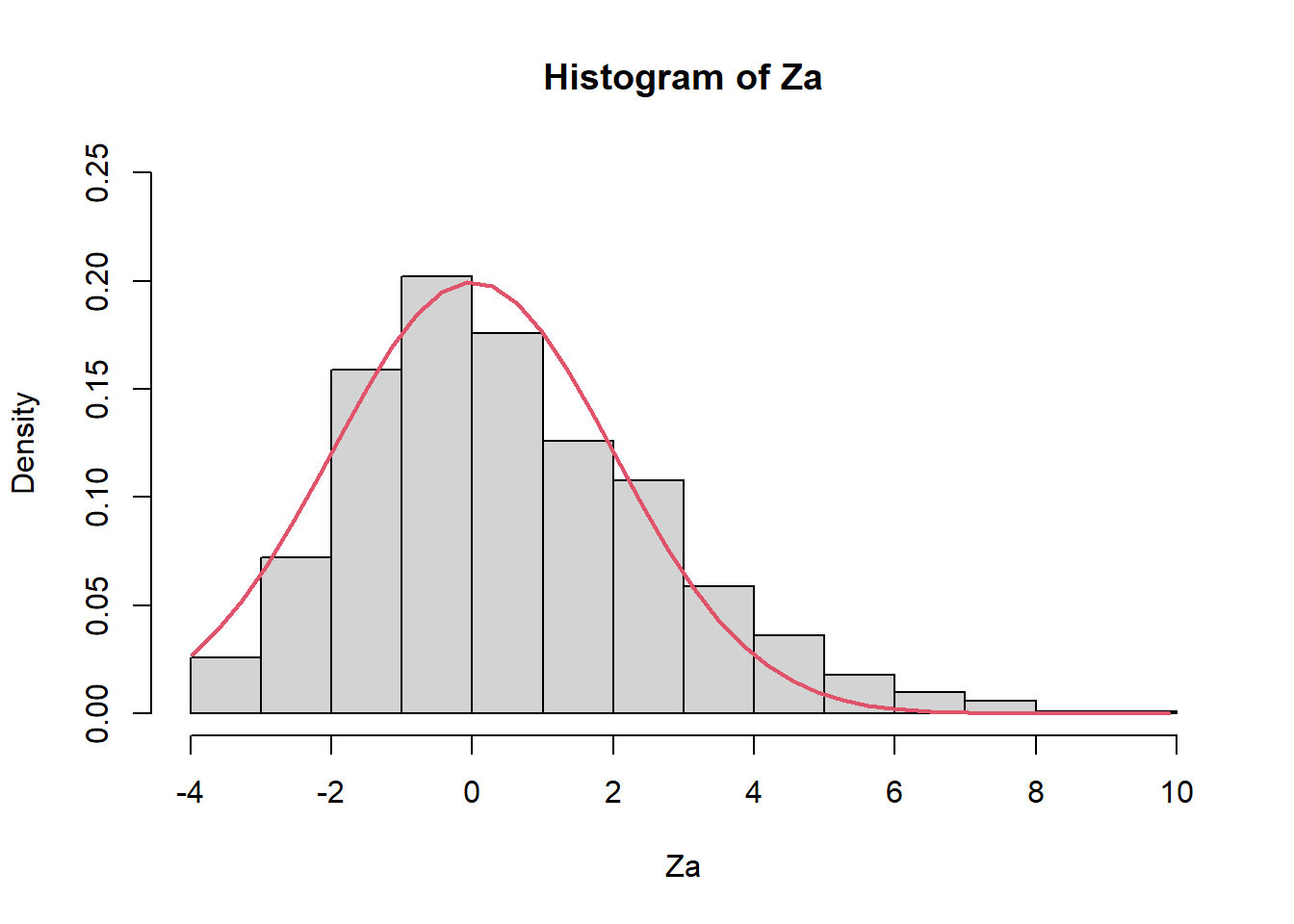

mean(Za)

[1] 0.4399522

var(Za)

[1] 5.499791

1.3 Veamos qué pasaría con n grande (n=150).

K <- 1000
n <- 150
X <- list()
for(i in 1:K){
  X[[i]] <- rexp(n,2) #X es una lista de las K muestras de tamaño 45.
}

media_X <- sapply(X,mean)
inv_media_X <- 1/media_X
Za=sqrt(n)*(inv_media_X-(1/0.5))
hist(Za,prob=TRUE,ylim=c(0,0.25))
Z2 <- seq(min(Za), max(Za), length = 40)
lines(Z2, dnorm(Z2, mean = 0, sd = sqrt(0.5^2/0.5^4)), col = 2, lwd = 2)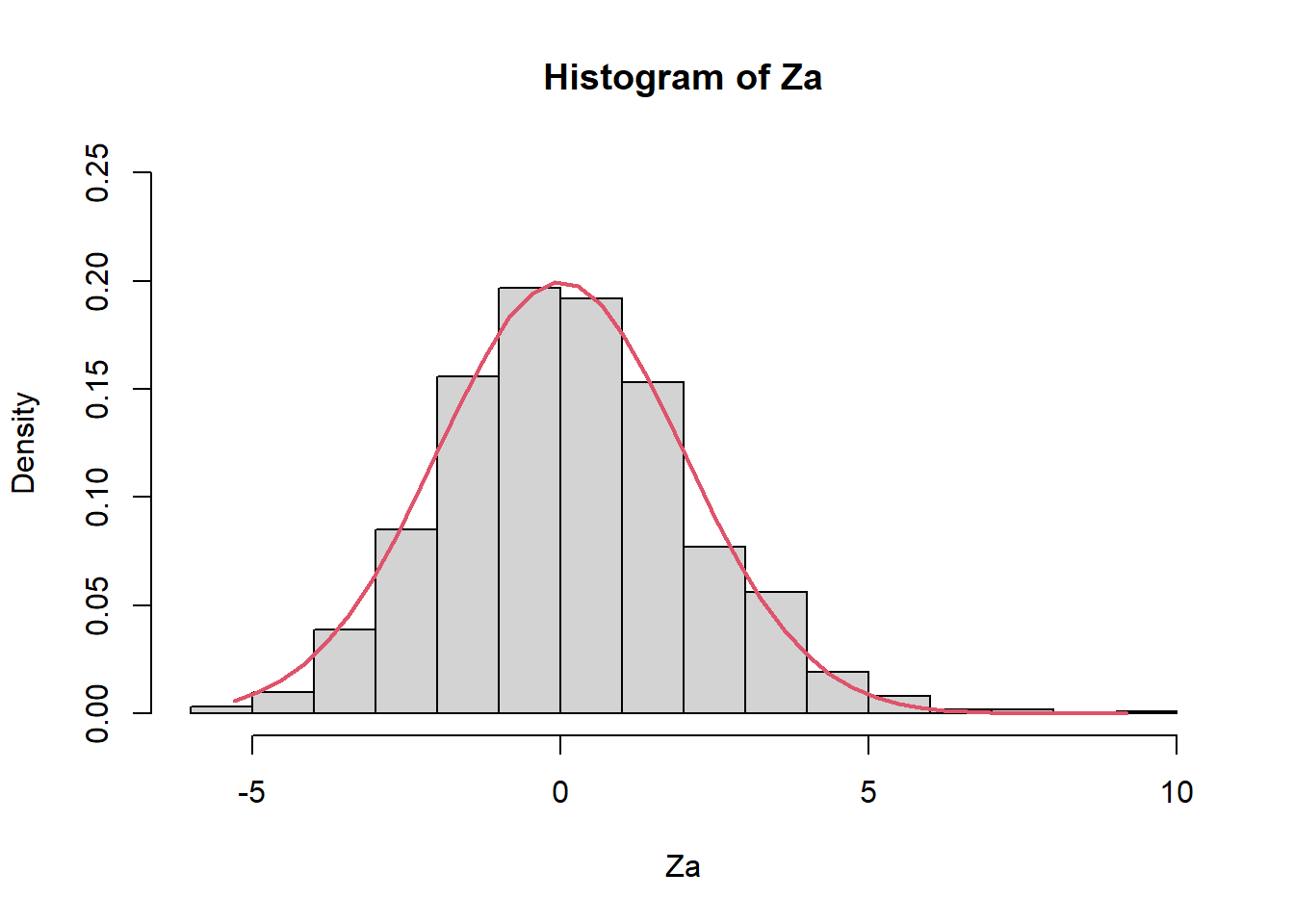

mean(Za)

[1] 0.1473689

var(Za)

[1] 4.204748

1.4 Veamos qué pasaría con n grande (n=300).

K <- 1000
n <- 300
X <- list()
for(i in 1:K){
  X[[i]] <- rexp(n,2) #X es una lista de las K muestras de tamaño 45.
}

media_X <- sapply(X,mean)
inv_media_X <- 1/media_X
Za=sqrt(n)*(inv_media_X-(1/0.5))
hist(Za,prob=TRUE,ylim=c(0,0.25))
Z2 <- seq(min(Za), max(Za), length = 40)
lines(Z2, dnorm(Z2, mean = 0, sd = sqrt(0.5^2/0.5^4)), col = 2, lwd = 2)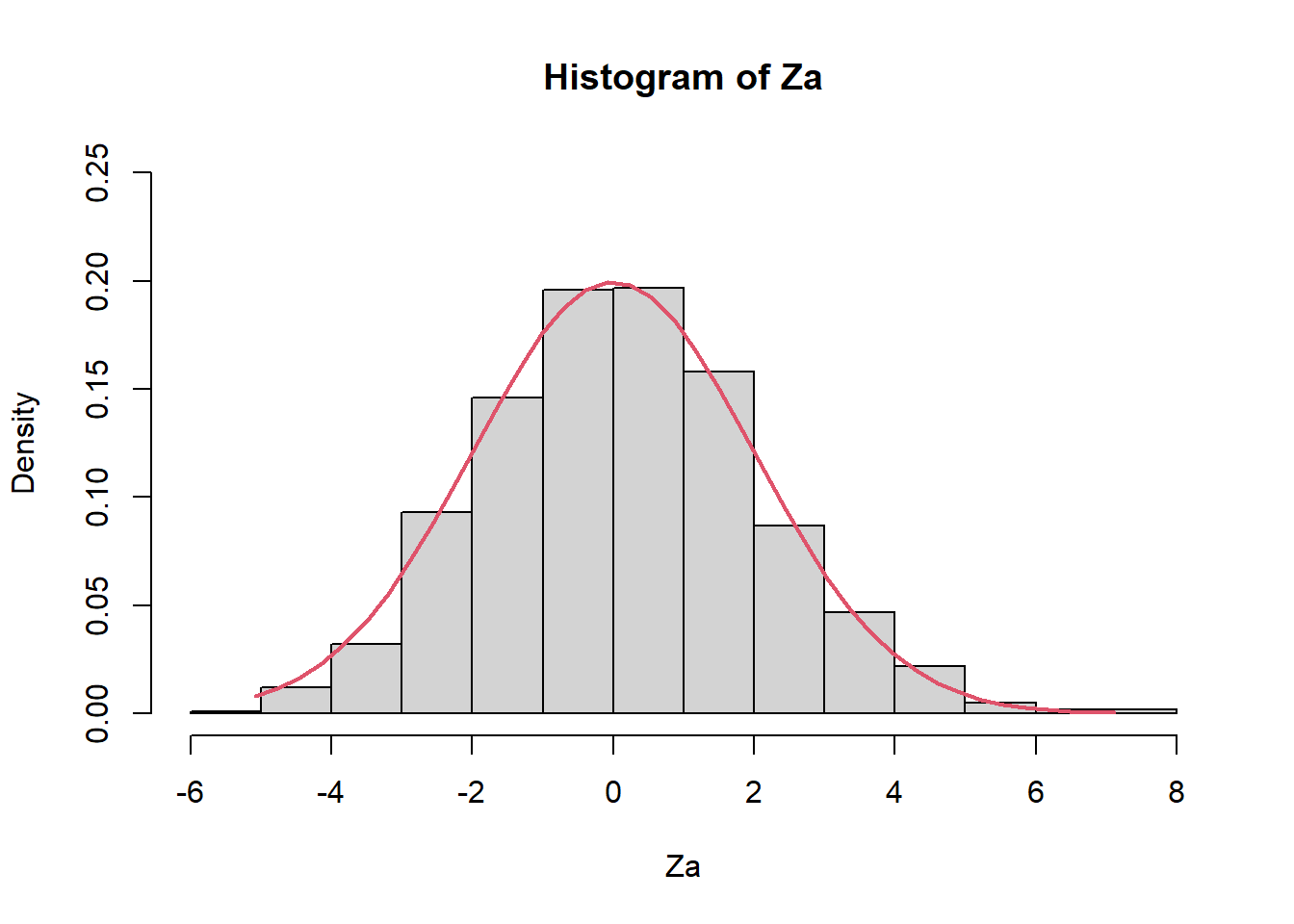

mean(Za)

[1] 0.2009543

var(Za)

[1] 4.09065

2 Comportamiento del EMV de la desviación estándar de una población normal

Suponga que \(X_1,...,X_n \sim N(0,2)\).

K <- 1000
n <- 30
X <- list()
for(i in 1:K){
  X[[i]] <- rnorm(n=n,mean=0,sd=sqrt(2)) 
}

Considere el EMV de \(\sigma\):

\[\hat{\sigma} = \left[\frac{\sum\limits_{i=1}^n X_{j}^2}{n}\right]^{1/2}.\]

sd_MV <- function(x){
  n <- length(x)
  sd_MV <- sqrt(sum(x^2)/n)
  return(sd_MV)
}

sd_MV_X <- sapply(X,sd_MV)
hist(sd_MV_X)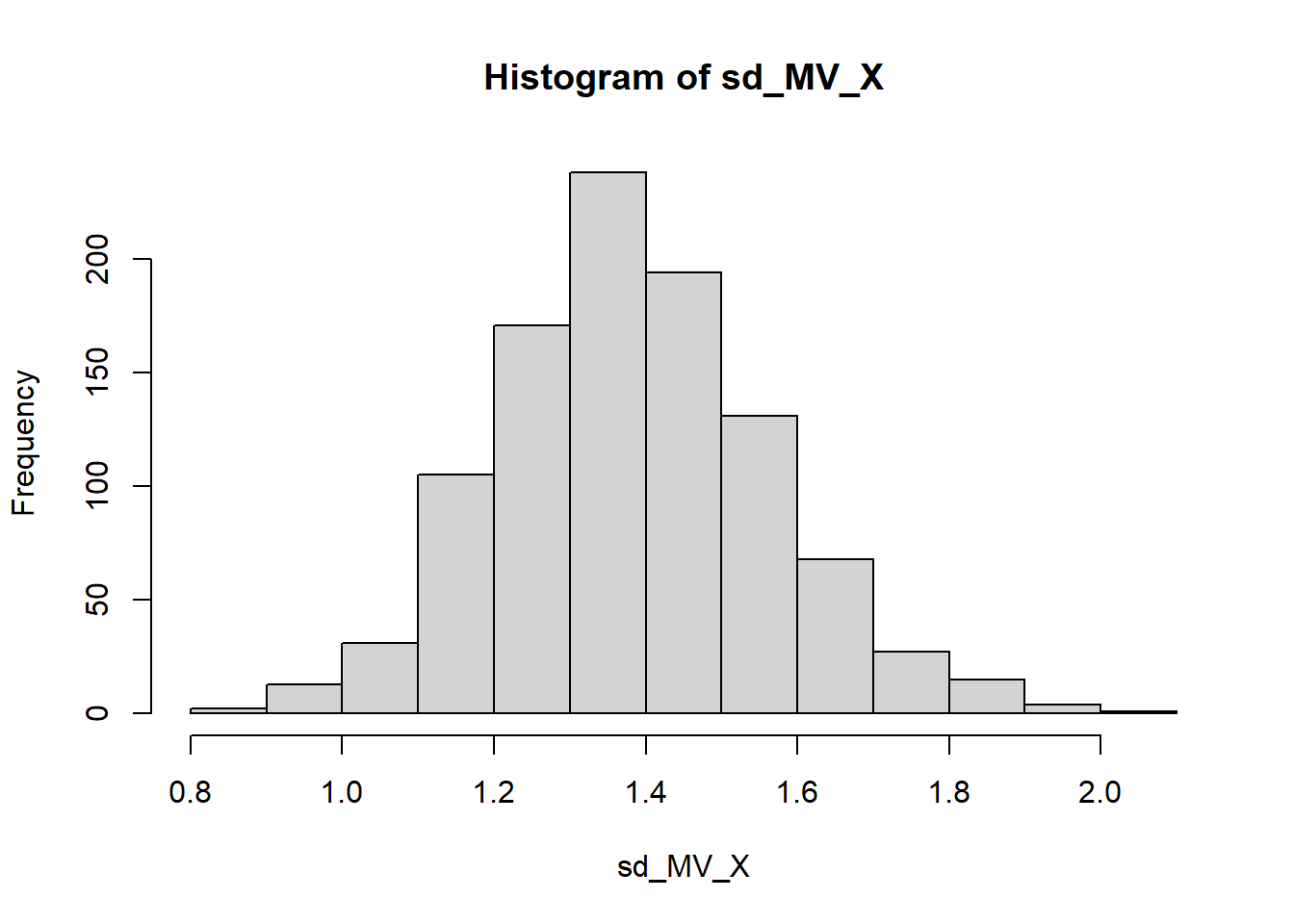

mean(sd_MV_X)

[1] 1.404725

var(sd_MV_X)

[1] 0.03574322

Sabemos que para muestras grandes, la distirbución de \(\hat{\sigma}\) converge a una distirbución normal con media \(\sigma=\sqrt{2} \approx 1.41\) y variancia \(1/[I(\sigma)]=\left(\frac{2n}{ \sigma^2}\right)^{-1}=\left( \frac{2 \cdot 30}{2} \right)^{-1} =1/30\approx 0.0334\).

Finalmente, podemos presentar el resultado usando la otra expresión:

\[\left[\frac{2n}{\sigma^2} \right]^{1/2}(\hat{\sigma}_n - \sigma) \stackrel{d}{\longrightarrow} N(0,1)\]

Za=sqrt(2*n/2)*(sd_MV_X-sqrt(2))
hist(Za,prob=TRUE,ylim=c(0,0.5))
Z2 <- seq(min(Za), max(Za), length = 40)
lines(Z2, dnorm(Z2, mean = 0, sd = 1), col = 2, lwd = 2)

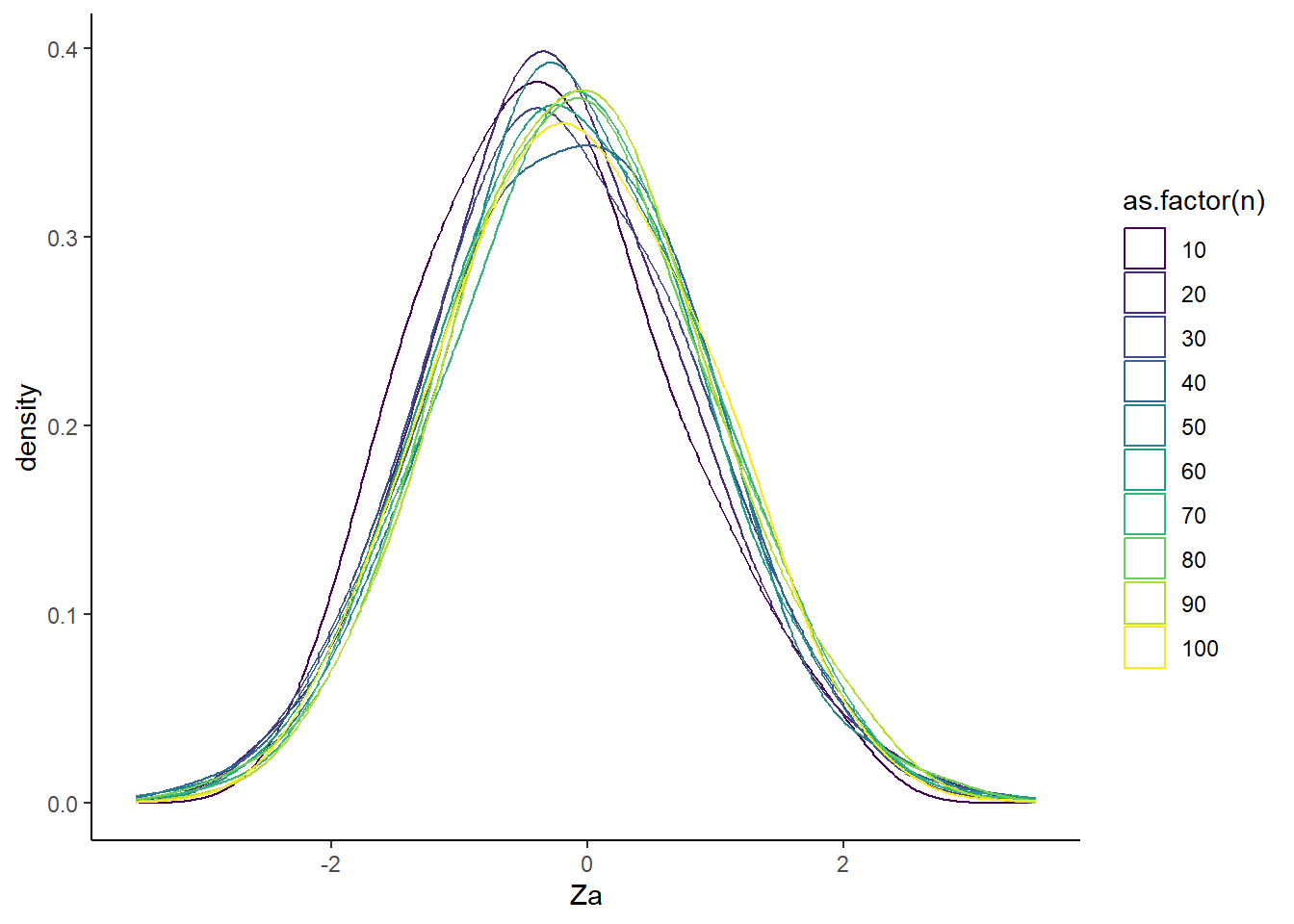
mean(Za)

[1] -0.0519693

var(Za)

[1] 1.072296

2.1 Visualización variando \(n\)

K <- 1000
N <- c(10,20,30,40,50,60,70,80,90,100)
sd_MV_estimador <- list()
sd_MV_X <- list()
for(n in 1:length(N)){
  for(i in 1:K){
    x <- rnorm(n=N[n],mean=10,sd=sqrt(2)) 
    sd_MV_X[i] <- sd_MV(x)
  }
  sd_MV_X <- unlist(sd_MV_X)
  
  Za = sqrt(2*N[n]/2)*(sd_MV_X-sqrt(2))
    sd_MV_estimador[[n]]= data.frame(Za,n=N[n])
}

resultados = rlist::list.rbind(sd_MV_estimador)

library(ggplot2)
library(hrbrthemes)

Warning: package 'hrbrthemes' was built under R version 4.4.3

library(viridis)

Warning: package 'viridis' was built under R version 4.4.3

Loading required package: viridisLite

p2 <- ggplot(data=resultados, aes(x=Za, color=as.factor(n))) +
    geom_density(adjust=1.5) +
    theme_classic()+ scale_color_viridis(discrete = TRUE, option = "D")

p2