lab04a: Contraste de hipótesis

XS3310 Teoría Estadística

Autor/a

Afiliación

Shu Wei Chou Chen

Escuela de Estadística (UCR)

Este documento ilustra de manera intuitiva, por medio de simulaciones, el concepto del contraste de hipótesis, específicamente el contraste uniformemente más potente.

1 Paquetes

library(dplyr)
library(ggplot2)
set.seed(1000)

2 Ejemplo con la distribución exponencial

Un banco asegura que el tiempo de espera del cliente en las cajas sigue una distribución exponencial con media \(\beta_0\). El gerente recibió quejas de los clientes de que el tiempo promedio de espera debe ser más. Decidió recolectar una muestra aleatoria de \(n\) clientes para ver contrastar dos hipótesis: \(H_0: \beta=\beta_0\) contra \(H_1: \beta>\beta_0\).

2.1 Encuentre el contraste uniformemente más potente (CUMP) de tamaño \(\alpha_0\) para contrastar estas hipótesis.

Tenemos dos formas de resolver de encontrar el CUMP de tamaño \(\alpha_0\).

Replanteando la hipótesis alternativa como \(H_1: \beta=\beta_1\) tal que \(\beta_1>\beta0\), tenemos dos hipótesis simples. Por lo que se puede aplicar el lema de Neymann-Pearson. De esta forma, el contraste más potente consiste en una región crítica de la forma:

\[RC= \left\lbrace X| \frac{\mathcal{L}(\beta_0)}{\mathcal{L}(\beta_1)}<k \right\rbrace.\] Es decir, la región crítica está dada por \[\frac{\mathcal{L}(\beta_0)}{\mathcal{L}(\beta_1)} = \frac{\frac{1}{\beta_0^n} e^{-\frac{1}{\beta_0}\sum{X_i}}}{ \frac{1}{\beta_1^n} e^{-\frac{1}{\beta_1}\sum{X_i}}}= \left(\frac{\beta_1}{\beta_0}\right)^n e^{-\sum{X_i}\left(\frac{1}{\beta_0}-\frac{1}{\beta_1}\right)}<k.\]

Se puede despejar el estadístico \(T=\sum{X_i}\) y concluir que la región crítica está dada por: \[\sum{X_i}>\frac{\ln\left[k\left(\frac{\beta_0}{\beta_1}\right)^n\right]}{-\left(\frac{1}{\beta_0}-\frac{1}{\beta_1}\right)}=k'.\] Luego, para asegurar que el contraste tenga tamaño \(\alpha_0\), se procede calcular el valor de \(k'\) por medio de la función potencia.

\[\alpha_0=\operatorname{Potencia}(\beta_0)=\operatorname{P}\left(\sum{X_i}>k'|\beta=\beta_0\right)=\operatorname{P}\left(\frac{2}{\beta}\sum{X_i}> \frac{2}{\beta}k'\left|\beta=\beta_0 \right.\right)\] \[=\operatorname{P}\left(\frac{2}{\beta_0}\sum{X_i}> \frac{2}{\beta_0}k'\right),\]

Como sabemos que \(\sum{X_i}\sim \operatorname{Gamma}(n,\beta)\) y \(\frac{2}{\beta}\sum{X_i}\sim \chi^2_{(2n)}\), su probabilidad de la cola derecha se puede encontrar por medio de tablas o programas estadísticos:

\[\alpha_0=\operatorname{P}\left(\chi^2_{(2n)}> \chi^2_{(1-\alpha_0,2n)}\right).\] Luego, \(\frac{2}{\beta_0}k'= \chi^2_{(1-\alpha_0,2n)}\) Es decir el contraste más potente de tamaño \(\alpha_0\) consiste en rechazar \(H_0\) si \[\sum{X_i}>k'=\frac{\beta_0}{2}\chi^2_{(1-\alpha_0,2n)}.\] Note que es equivalente dejar en término de la distribución \(\chi^2\), es decir una región crítica que consiste en \(\frac{2}{\beta_0}\sum{X_i}>\chi^2_{(1-\alpha_0,2n)}\).

Por ejemplo, si \(n=10\), \(\beta_0=5\) y \(\alpha_0=0.05\), el contraste más potente con tamaño \(0.05\) consiste en rechazar \(H_0\) si \[\sum{X_i}>k'=\frac{\beta_0}{2}\chi^2_{(1-\alpha_0,2n)}.\]

n <- 10
5/2*qchisq(p=0.95,df= 2*n)

[1] 78.52608

Finalmente, note que la región crítica no depende del valor \(\beta_1\) de la hipótesis alternativa, por lo que se puede garantizar que este contraste es uniformemente más potente con tamaño \(\alpha_0\) para \(\Omega_1 = (\beta_0,\infty)\).

El segundo método consiste en demostrar que dado \(\beta_0<\beta_1\),

\[\frac{\mathcal{L}(\beta_0)}{\mathcal{L}(\beta_1)} = \left(\frac{\beta_1}{\beta_0}\right)^n e^{-\sum{X_i}\left(\frac{1}{\beta_0}-\frac{1}{\beta_1}\right)}\] es una función decreciente en \(\sum X_i\), entonces el CUMP con tamaño \(\alpha_0\) existe y tiene la región crítica dada por \(\sum X_i>k\). Luego, encontrar el valor de \(k\) sigue un procedimiento similar.

2.2 Suponga que \(\beta_0=5\), \(n=10\) y \(\alpha_0=0.05\). Grafique la función potencia del contraste encontrado en 1.

La función potencia se define como la probabilidad de rechazar la hipótesis nula dado un valor de \(\beta\), o sea \[\operatorname{Potencia}(\beta)=\operatorname{P}\left(\frac{2}{\beta_0}\sum{X_i}>\chi^2_{(1-\alpha_0,2n)}|\beta\right)=\operatorname{P}\left(\frac{2}{5}\sum{X_i}>\chi^2_{(0.95,20)}|\beta\right)\] \[=\operatorname{P}\left(\sum{X_i}>\frac{5}{2}\chi^2_{(0.95,20)}|\beta\right)\]

\[=\operatorname{P}\left(\sum{X_i}>78.5261|\beta\right)=\operatorname{P}\left(\sum{X_i}>78.5261|\beta\right).\]

Por ejemplo, para \(\beta=10\), tenemos que \(\sum{X_i}\sim \operatorname{Gamma}(n=10,\beta=10)\). Su probabilidad de la cola derecha a partir de \(78.525\) es dada por

beta <- 10
1-pgamma(78.525,shape=n,scale=beta)

[1] 0.7347486

Es decir \(\operatorname{Potencia}(10)=0.7347.\)

Si se quiere evaluar en un rango de valores

beta <- seq(0.01, 15, by=0.01)
Potencia <- 1-pgamma(78.525,shape=n,scale=beta)
Pot <- data.frame(beta,Potencia)
ggplot(data=Pot, aes(x=beta, y=Potencia)) +
  geom_line() + theme_bw()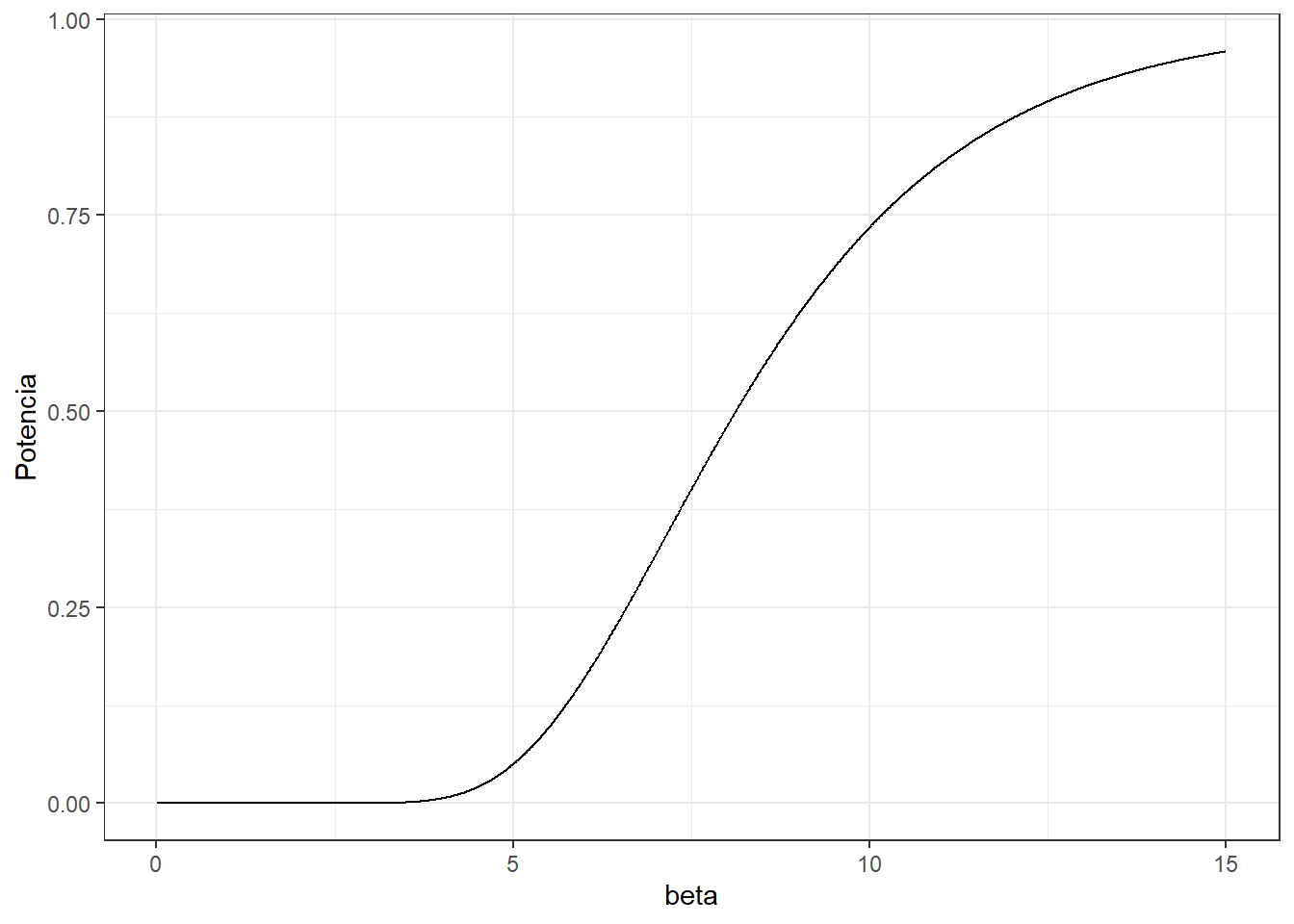

Por ejemplo, la potencia evaluada cuando \(H_0\) es cierta (\(\beta=5\)) es

beta <- 5
1-pgamma(78.525,shape=n,scale=beta)

[1] 0.05000524

que es el tamaño del contraste \(\alpha_0=0.05\).

2.3 Suponga que el tiempo promedio verdadero es \(\beta=15\). Simule una muestra aleatoria de tamaño \(n=10\). Concluya el problema.

Se simula una muestra aleatoria de tamaño \(10\), suponiendo que la población es exponencial con parámetro \(15\).

muestra <- rexp(n=10, rate = 1/15)
muestra

 [1] 15.0699303  7.7653946 36.5607662 32.4487335  7.1614457  2.5060514
 [7] 23.4573732  7.6638474 14.4222626  0.7577991

sum(muestra)

[1] 147.8136

Como \(\sum{X_i}=\) 147.8136 \(> \frac{5}{2}\chi^2_{(1-\alpha_0,20)}=78.52\). Por lo que se rechaza la hipótesis nula con un nivel de significancia de \(0.05\).

2.4 Repita el ejercicio 3 pero suponiendo que el tiempo promedio verdadero es \(\beta=11\). Simule una muestra aleatoria de tamaño \(n=10\). Concluya el problema.

Se simula una muestra aleatoria de tamaño \(10\), suponiendo que la población es exponencial con parámetro \(11\).

muestra <- rexp(n=10, rate = 1/11)
muestra

 [1]  8.271628 18.588359  6.708886  9.367997 24.505987  1.062720  3.884172
 [8]  8.316690 23.252876  3.888139

sum(muestra)

[1] 107.8475

Como \(\sum{X_i}=\) 107.8475 \(> \frac{5}{2}\chi^2_{(1-\alpha_0,20)}=78.52\). Por lo que se rechaza la hipótesis nula con un nivel de significancia de \(0.05\).