Tema A: Repaso de estadística multivariada
Variable aleatoria de dimensión \(p\)
Contenido
Variable aleatoria de dimensión \(p\)
Un vector aleatorio (o una variable aleatoria) de dimensión \(p\) es un vector columna \(\mathbf{X}=(X_1,...,X_p)'\) con cada componente como una variable aleatoria.
La distribución conjunta \(F\) de \(\mathbf{X}\) es definida como \[F\left(x_1, \ldots, x_p\right)=\operatorname{P}\left[X_1, \leq x_1, \ldots, X_p \leq x_p\right],\label{eq:distconjunta} \qquad(1)\] para todos los números reales \(x_1, \ldots, x_p\).
De manera compacta, se escribe \[F(\mathbf{x})=\operatorname{P}[\mathbf{X} \leq \mathbf{x}],\] para todos vectores reales \(\mathbf{x} = (x_1, \ldots, x_p)'\).
- La distribución conjunta de cualquier subcolección de \(X_{i_1},...,X_{i_k}\) se puede obtener evaluando \(x_j = \infty\) en la Ecuación 1, para \(j \notin \left\lbrace i_1,...,i_k \right\rbrace\).
Ejemplo 1
- La distribución de \(X_1\) es
\[F_{X_1}\left(x_1\right)=\operatorname{P}\left[X_1 \leq x_1\right]=F\left(x_1, \infty, \ldots, \infty\right).\]
- La distribución de \((X_1,X_{p-1})'\) es
\[\begin{aligned} F_{X_1, X_{p-1}}\left(x_1, x_{p-1}\right)& = \operatorname{P}\left[X_1 \leq x_1, X_{p-1} \leq x_{p-1}\right] \\ & =F\left(x_1, \infty, \ldots, \infty, x_{p-1},\infty\right). \end{aligned}\]
Distribución continua y discreta
- Similar a las variables aleatorias univariadas, un vector aleatorio \(\mathbf{X}\) es continuo, si \(F\) tiene una función densidad, es decir, \[F\left(x_1, \ldots, x_p\right)=\int_{-\infty}^{x_p} \cdots \int_{-\infty}^{x_2} \int_{-\infty}^{x_1} f\left(y_1, \ldots, y_p\right) d y_1 d y_2 \cdots d y_p.\] La función de densidad de \(\mathbf{X}\) se obtiene con
\[f\left(x_1, \ldots, x_p\right)=\frac{\partial^p F\left(x_1, \ldots, x_p\right)}{\partial x_1 \cdots \partial x_p}.\]
- Se dice que \(\mathbf{X}\) es discreto, si existen vectores reales \(\mathbf{x}_0, \mathbf{x}_1,...\) y una función de masa de probabilidad \(p(\mathbf{x}_j)=\operatorname{P}[\mathbf{X} = \mathbf{x}_j]\) tal que \[ \sum_{j=0}^\infty p(\mathbf{x}_j) = 1.\]
Esperanza matemática
- La esperanza matemática de una función \(g\) de un vector aleatorio se define como
\[\operatorname{E}(g(\mathbf{X}))=\int g(\mathbf{x}) d F(\mathbf{x})=\int g\left(x_1, \ldots, x_p\right) d F\left(x_1, \ldots, x_p\right),\] donde
\[\begin{aligned} & \int g\left(x_1, \ldots, x_p\right) d F\left(x_1, \ldots, x_p\right) \\ & \quad= \begin{cases}\int\limits \cdots \int\limits g\left(x_1, \ldots, x_p\right) f\left(x_1, \ldots, x_p\right) d x_1 \cdots d x_p, & \text {(caso continuo)} \\ \sum\limits_{j_1} \cdots \sum\limits_{j_p} g\left(x_{j_1}, \ldots, x_{j_p}\right) p\left(x_{j_1}, \ldots, x_{j_p}\right), & \text { (caso discreto)}\end{cases} \end{aligned}\]
y \(g\) es cualquier función tal que \(E|g(\mathbf{X})|<\infty\).
Independencia
- Las variables aleatorias \(X_1,...,X_p\) son independientes, si \[P\left[X_1 \leq x_1, \ldots, X_p \leq x_p\right]=\operatorname{P}\left[X_1 \leq x_1\right] \cdots \operatorname{P}\left[X_p \leq x_p\right].\] Es decir,
\[F\left(x_1, \ldots, x_p\right)=F_{X_1}\left(x_1\right) \cdots F_{X_p}\left(x_p\right).\]
- El concepto de independencia también se puede expresar en términos de función de densidad:
\[f\left(x_1, \ldots, x_p\right)=f_{X_1}\left(x_1\right) \cdots f_{X_p}\left(x_p\right), \qquad(2)\] y función de probabilidad:
\[p\left(x_1, \ldots, x_p\right)=p_{X_1}\left(x_1\right) \cdots p_{X_p}\left(x_p\right).\]
Distribución condicional
- Para dos vectores aleatorios \(\mathbf{X}= (X_1,...,X_p)'\) y \(\mathbf{Y}= (Y_1,...,Y_q)'\) con función de densidad conjunta \(f_{\mathbf{X},\mathbf{Y}}\), la distribución condicional de \(\mathbf{Y}\) dado \(\mathbf{X}=\mathbf{x}\) es
\[f_{\mathbf{Y} \mid \mathbf{X}}(\mathbf{y} \mid \mathbf{x})= \begin{cases}\frac{f_{\mathbf{X}, \mathbf{Y}}(\mathbf{x}, \mathbf{y})}{f_{\mathbf{X}}(\mathbf{x})}, & \text { si } f_{\mathbf{X}}(\mathbf{x})>0, \\ f_{\mathbf{Y}}(\mathbf{y}), & \text { si } f_{\mathbf{X}}(\mathbf{x})=0.\end{cases} \qquad(3)\]
- La esperanza condicional de \(g(\mathbf{Y})\) dado \(\mathbf{X}=\mathbf{x}\) es
\[\operatorname{E}(g(\mathbf{Y}) \mid \mathbf{X}=\mathbf{x})=\int_{-\infty}^{\infty} g(\mathbf{y}) f_{\mathbf{Y} \mid \mathbf{X}}(\mathbf{y} \mid \mathbf{x}) d \mathbf{y}\]
Si \(\mathbf{X}\) y \(\mathbf{Y}\) son independientes, entonces \(f_{\mathbf{Y} \mid \mathbf{X}}(\mathbf{y} \mid \mathbf{x})=f_{\mathbf{Y}}(\mathbf{y})\). (Por Ecuación 2 y Ecuación 3)
Como consecuencia, la esperanza condicional de \(g(\mathbf{Y})\) dado \(\mathbf{X}=\mathbf{x}\) es
\[\operatorname{E}(g(\mathbf{Y}) \mid \mathbf{X}=\mathbf{x})=\operatorname{E}(g(\mathbf{Y})),\] el cual no depende de \(\mathbf{x}\).
- Para el caso discreto es igual pero con función de probabilidad.
Medias y covariancias
- Si \(\operatorname{E}|X_i|< \infty\) para cada \(i\), entonces defina la media o el valor esperado de \(\mathbf{X}=(X_1,...,X_p)\) como el vector columna \[\mathbf{\mu}_\mathbf{X} = \operatorname{E}(\mathbf{X})= \left[\operatorname{E}(X_1),...,\operatorname{E}(X_p)\right]'.\]
- Si \(\mathbf{X}=(X_1,...,X_p)'\) y \(\mathbf{Y}=(Y_1,...,Y_q)'\) son vectores aleatorios tal que cada \(X_i\) y \(Y_j\) tiene variancia finita, entonces la matriz de covariancia de \(\mathbf{X}\) y \(\mathbf{Y}\) es definida como
\[\begin{align} \Sigma_{\mathbf{XY}} =& \operatorname{Cov}(\mathbf{X},\mathbf{Y}) = \operatorname{E}\left[ (\mathbf{X}-\mu_\mathbf{X})(\mathbf{Y}-\mu_\mathbf{Y})' \right] \\ =& \operatorname{E} (\mathbf{X}\mathbf{Y}) - \mu_\mathbf{X} \mu_\mathbf{Y}'. \end{align}\]
El elemento \((i,j)\) de \(\Sigma_{\mathbf{XY}}\) es la covariancia \(\operatorname{Cov}(X_i,Y_j)=\operatorname{E}(X_i Y_j) - \mu_{X_i} \mu_{Y_j}\).
Si \(\mathbf{Y}=\mathbf{X}\), \(\Sigma_{\mathbf{XY}}= \operatorname{Cov}(\mathbf{X},\mathbf{Y})\) se reduce a \(\Sigma_{\mathbf{XX}}= \operatorname{Cov}(\mathbf{X},\mathbf{X}):=\Sigma_{\mathbf{X}}\).
Propiedades
- Sea \(\mathbf{X}\) un vector aleatorio de dimensión \(p\), y defina la variable \(\mathbf{Z}=a+B\mathbf{X}\), donde \(\mathbf{a}\) es un vector columna \((p \times 1)\), y \(\mathbf{B}\) es una matriz \(q \times p\). Entonces, la \(\mathbf{Y}\) tiene media y matriz de covariancia como siguen:
\[\mu_{\mathbf{Y}} = \operatorname{E}(\mathbf{Y})= \mathbf{a} + \mathbf{B} \operatorname{E}(\mathbf{X}),~~~~~\text{y}~~\Sigma_{\mathbf{YY}}=\mathbf{B}\Sigma_{\mathbf{XX}} \mathbf{B}'.\]
Proposición 1 La matriz de covariancia \(\Sigma_{\mathbf{X}}\) de un vector aleatorio \(\mathbf{X}\) es simétrica y definida no negativa, es decir \[\mathbf{b}'\Sigma_{\mathbf{X}}\mathbf{b} \geq 0,\] para cualquier vector \(\mathbf{b}=(b_1,...,b_p)'\).
Proposición 2 Toda matriz de covariancia \(n \times n\), \(\Sigma\) se puede factorizar como \[ \Sigma = P \Lambda P'\] donde \(P\) es una matriz ortogonal (es decir, \(P'=P^{-1}\)) cuyas columnas son un conjunto ortonormal de autovectores corresondientes a los autovalores \(\lambda_1,...,\lambda_p\) de \(\Sigma\) y \(\Lambda\) es la matriz diagonal \[\Lambda=\left[\begin{array}{llll} \lambda_1 & 0 & \cdots & 0 \\ 0 & \lambda_2 & \cdots & 0 \\ \vdots & \vdots & \ddots & \vdots \\ 0 & 0 & \cdots & \lambda_n \end{array}\right].\]
Específicamente, \(\Sigma\) es no singular si y solo si todos los autovalores son estrictamente positivos.
Nota
Dada una matriz de covariancia \(\Sigma\), es común y útil encontrar su raíz cuadrada \(A=\Sigma^{1/2}\) que cumple la condición \(AA'=\Sigma\). De Proposición 2, se puede deducir que
\[A=\Sigma^{1/2}= P\Lambda^{1/2}P'.\] Note que \(AA'=\Sigma^{1/2}= P\Lambda^{1/2}P'P\Lambda^{1/2}P'=P\Lambda P'.\)
Distribución normal bivariada
Contenido
Distribución normal bivariada
Un vector aleatorio \(\mathbf{X}= (X_1,X_2)'\) es binormal (o normal bivariado), si su densidad es \[f_{\mathbf{X}}(\mathbf{x})= \frac{1}{2 \pi \sigma_1 \sigma_2\left(1-\rho^2\right)^{1 / 2}} e^{-\frac {1} { 2 ( 1 - \rho^2) } \left[\left(\frac{x_1-\mu_1}{\sigma_1}\right)^2\right.\left.-2 \rho\left(\frac{x_1-\mu_1}{\sigma_1}\right)\left(\frac{x_2-\mu_2}{\sigma_2}\right)+\left(\frac{x_2-\mu_2}{\sigma_2}\right)^2\right]}.\]
Más adelante, veremos que esta distribución es un caso particular de la distribución normal multivariada con media \[\mathbf{\mu}=\begin{pmatrix} \mu_1 \\ \mu_2 \end{pmatrix},\] y matriz de covariancia \[\Sigma=\left[\begin{array}{cc} \sigma_1^2 & \rho \sigma_1 \sigma_2 \\ \rho \sigma_1 \sigma_2 & \sigma_2^2 \end{array}\right], \quad \sigma_1>0, \sigma_2>0, -1<\rho<1.\]
Los parámetros \(\sigma_1^2\), \(\sigma_1^2\) y \(\rho\) son desviaciones estándares de los componentes \(X_1\) y \(X_2\) y la correlación, respectivamente.
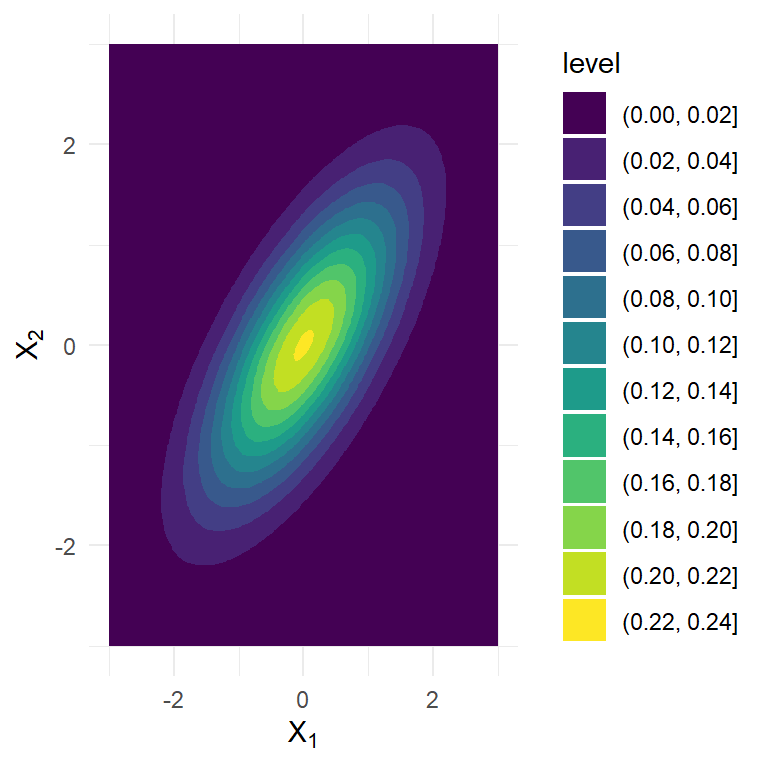
Ejemplo 2 La visualización de la densidad de una binormal con \[\mathbf{\mu}=\begin{pmatrix} 0 \\ 0 \end{pmatrix}, ~~\text{y} ~~~\Sigma=\left[\begin{array}{cc} 1 & 0.7 \\ 0.7 & 1 \end{array}\right].\]

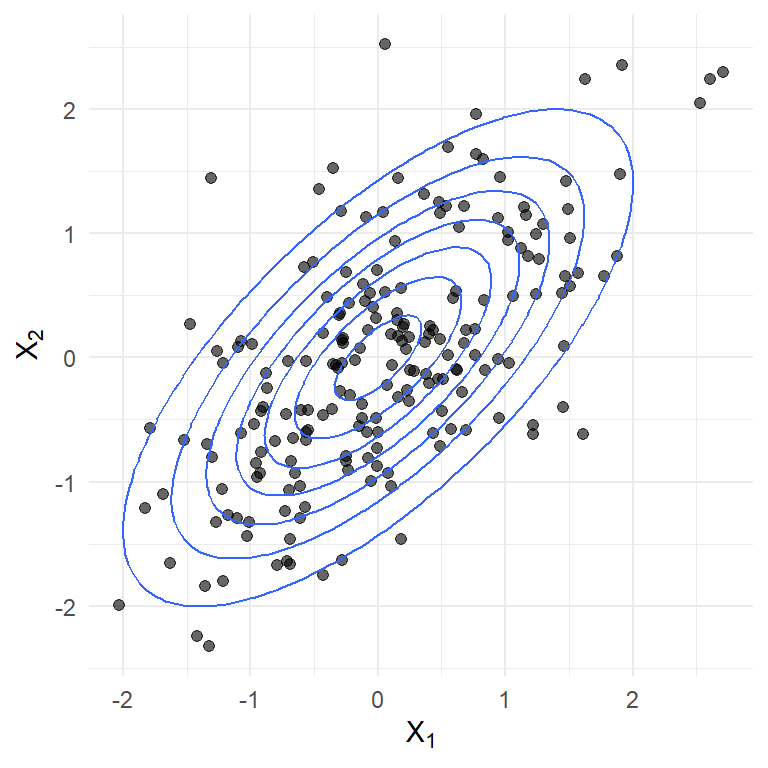
Figura 3: Muestra aleatoria de una binormal (n=200) y contornos de densidad teórica.
Distribución normal multivariada
Contenido
Distribución normal multivariada
La distribución normal multivariada es una de las distribuciones más importantes en estadística.
Sea \(\mathbf{X}=(X_1,...,X_p)'\) un vector aleatorio. \(\mathbf{X}\) tiene distribución normal multivariada con media \(\mathbf{\mu}\) y matriz de covariancia \(\Sigma=\Sigma_{XX}\) (no singular), denotada por \(\mathbf{X} \sim N(\mathbf{\mu},\Sigma)\), si \[f_{\mathbf{X}}(\mathbf{x})=(2 \pi)^{-n / 2}(\operatorname{det} \Sigma)^{-1 / 2} \exp \left\{-\frac{1}{2}(\mathbf{x}-\boldsymbol{\mu})^{\prime} \Sigma^{-1}(\mathbf{x}-\boldsymbol{\mu})\right\}.\]
Propiedades
Si \(\mathbf{X} \sim N(\mathbf{\mu},\Sigma_X)\), entonces podemos definir el vector aleatorio estandarizado, aplicando \[\mathbf{Z}=\Sigma^{-1/2}(\mathbf{X}-\mu).\] Como resultado, \(\mathbf{Z}\) tiene media \(\mathbf{0}\) y \(\Sigma_{ZZ}=I_p\), una matriz de identidad \(p \times p\).
Usando el método del cambio de variables, la densidad de \(\mathbf{Z}\) es dada por: \[\begin{aligned} f_{\mathbf{Z}}(\mathbf{z}) & =(\operatorname{det} \Sigma)^{1 / 2} f_{\mathbf{X}}\left(\Sigma^{1 / 2} \mathbf{z}+\boldsymbol{\mu}\right) \\ & =(\operatorname{det} \Sigma)^{1 / 2}(2 \pi)^{-n / 2}(\operatorname{det} \Sigma)^{-1 / 2} \exp \left\{-\frac{1}{2}\left(\Sigma^{-1 / 2} \mathbf{z}\right)^{\prime} \Sigma^{-1} \Sigma^{-1 / 2} \mathbf{z}\right\} \\ & =(2 \pi)^{-n / 2} \exp \left\{-\frac{1}{2} \mathbf{z}^{\prime} \mathbf{z}\right\} \\ & =\left((2 \pi)^{-1 / 2} \exp \left\{-\frac{1}{2} z_1^2\right\}\right) \cdots\left((2 \pi)^{-1 / 2} \exp \left\{-\frac{1}{2} z_p^2\right\}\right),\end{aligned}\] es decir, \(Z_1,...,Z_p\) son variables aleatorias i.i.d. \(N(0,1)\).
También se puede construir una distribución normal multivariada con media \(\mathbf{0}\) y matriz de covariancias \(\Sigma\), por medio de una distribución normal multivariada estándar: \[\mathbf{X}=\Sigma^{1 / 2} \mathbf{Z}+\mu.\]
- Si \(\mathbf{X} \sim N(\mathbf{\mu},\Sigma_X)\), \(B\) es una matriz \(q \times p\) y \(a\) es un vector \(q \times 1\), entonces el vector aleatorio \[\mathbf{Y}=a + B\mathbf{X}\] también es normal multivariado con media \(a + B\mathbf{\mu}\) y matriz de covariancias \(B\Sigma B'\).
- Podemos particionar \(\mathbf{X}\) en dos subvectores. \[\mathbf{X}=\left[\begin{array}{l} \mathbf{X}^{(1)} \\ \mathbf{X}^{(2)} \end{array}\right]\] Entonces, podemos escribir la matriz de media y covariancia de \(\mathbf{X}\) como \[\boldsymbol{\mu}=\left[\begin{array}{l} \boldsymbol{\mu}^{(1)} \\ \boldsymbol{\mu}^{(2)} \end{array}\right] \quad \text { and } \quad \Sigma=\left[\begin{array}{ll} \Sigma_{11} & \Sigma_{12} \\ \Sigma_{21} & \Sigma_{22} \end{array}\right],\] donde \(\boldsymbol{\mu}^{(i)}=\operatorname{E}\left( \mathbf{X}^{(i)}\right)\) y \(\Sigma_{i j}=\operatorname{E}\left[\left(\mathbf{X}^{(i)}-\boldsymbol{\mu}^{(i)}\right)\left(\mathbf{X}^{(j)}-\boldsymbol{\mu}^{(i)}\right)^{\prime}\right]\).
Proposición 3
\(\mathbf{X}^{(1)}\) y \(\mathbf{X}^{(2)}\) son idependientes si y solo si \(\Sigma_{12}=0\).
La distribución condicional de \(\mathbf{X}^{(1)}\) dado \(\mathbf{X}^{(2)}=\mathbf{x}^{(2)}\) es \(N\left(\boldsymbol{\mu}^{(1)}+\Sigma_{12} \Sigma_{22}^{-1}\left(\mathbf{x}^{(2)}-\right.\right. \left.\left.\boldsymbol{\mu}^{(2)}\right), \Sigma_{11}-\Sigma_{12} \Sigma_{22}^{-1} \Sigma_{21}\right).\) Específicamente, \[\operatorname{E}\left(\mathbf{X}^{(1)} \mid \mathbf{X}^{(2)}=\mathbf{x}^{(2)}\right)=\boldsymbol{\mu}^{(1)}+\Sigma_{12} \Sigma_{22}^{-1}\left(\mathbf{x}^{(2)}-\boldsymbol{\mu}^{(2)}\right).\]
Ejemplo 3
Sea \(\mathbf{X}=(X_1,X_2)\) una variable aleatoria binormal.
Podemos deducir que \(X_1\) y \(X_2\) son independientes si y solo si \(\rho \sigma_1 \sigma_2=0\) (es decir, \(\rho=0\)).
La distirbución condicional de \(X_1\) dado \(X_2\) es normal con media
\[\operatorname{E}(X_1 \mid X_2=x_2)= \mu_1 + \rho \sigma_1 \sigma_2^{-1}(x_2-\mu_2),\] y la variancia \[\operatorname{Var}(X_1 \mid X_2=x_2)= \sigma_1^2 (1-\rho^2).\]
Serie temporal gaussiana
Contenido
Serie temporal gaussiana
\(\left\{X_t\right\}\) es una serie temporal gaussiana (o modelo de serie temporal gaussiano) si todas sus distribuciones conjuntas son normales multivariadas, es decir, si para cualquier colección de números enteros \(i_1, \ldots, i_n\), el vector aleatorio \(\left(X_{i_1}, \ldots, X_{i_n}\right)^{\prime}\) tiene una distribución normal multivariada.
Nota
Si \(\{X_t\}\) es una serie temporal gaussiana, entonces todas sus distribuciones conjuntas son completamente determinadas por medio de la función media \(\mu_t=\operatorname{E}(X_t)\) y la función de autocovariancia \(\gamma(t,s)=\operatorname{Cov}(X_t,X_s)\).
Además, si el proceso es estacionario, entonces
- La función media es constante, \(\mu_t=\mu\) para todo \(t\),
- la función de autocovariancia \(\gamma(t,s)=\gamma(t,t+h)\) depende únicamente de \(h\), es decir podemos escribir \(\gamma(t,t+h):=\gamma(h)\).
- En este caso, la distribución de \(X_1,...,X_t\) es igual que la distribución de \(X_{1+h},...,X_{t+h}\), para todo \(h\) entero y \(t\) positivo.
- Se concluye que una serie temporal gaussiana es estrictamente estacionaria si y solo si es débilmente estacionaria.