Tema 3: Técnicas de suavizamiento exponencial
Paquetes de R
Para este tema, se necesita cargar estos paquetes:
Introducción
Contenido
Introducción
Suavizamiento exponencial simple (SES)
El método lineal de Holt
El método lineal de Holt amortiguado
El método multiplicativo y aditivo de Holt-Winters
Taxonomía de los métodos de SE
Representación como modelos de Espacio de Estados
Introducción
Desarrollados en los años 1950s.
Son aplicados ampliamente debido a su sencillez y bajo costo.
Pueden ser utilizados para pocas observaciones.
- Suavizamiento exponencial simple (SES)
- Método lineal de Holt (con tendencia)
- Métodos multiplicativo y aditivo de Holt-Winters (con estacionalidad)
Suavizamiento exponencial simple (SES)
Contenido
Introducción
Suavizamiento exponencial simple (SES)
El método lineal de Holt
El método lineal de Holt amortiguado
El método multiplicativo y aditivo de Holt-Winters
Taxonomía de los métodos de SE
Representación como modelos de Espacio de Estados
Suavizamiento exponencial simple (SES)
Es apropiada para serie que no tienen patrones estacionales ni de tendencia, y cuya media o nivel cambia lentamente.
Notación:
- \(Z_t\): la observación de la serie en el tiempo \(t\).
- \(P_t\): el pronóstico del tiempo \(t\).
- \(Z_t-P_t\): el error de pronóstico.
El método de SES consiste en: \[P_{t+1}=P_t+\alpha (Z_t-P_t)\] donde \(0\leq \alpha\leq1\) es el parámetro de suavizamiento.
- El pronóstico en el tiempo \(t+1\) es una combinación del pronóstico en el tiempo \(t\) y una proporción \(\alpha\) el error de pronóstico del tiempo \(t\).
Note que la ecuación anterior es equivalente a: \[P_{t+1}=\alpha Z_t + (1-\alpha)~ P_t\] i.e., el pronóstico en el tiempo \(t+1\) es un promedio ponderado de la observación más reciente y el pronóstico en el tiempo \(t\).
Recursivamente se obtienen: \[\begin{align*} P_{t+1} &= \alpha Z_t + (1 - \alpha) \left[ \alpha Z_{t-1} + (1 - \alpha) P_{t-1} \right] \\ &= \alpha Z_t + \alpha (1 - \alpha) Z_{t-1} + (1 - \alpha)^2 P_{t-1} \\ &= \alpha Z_t + \alpha (1 - \alpha) Z_{t-1} + \alpha (1 - \alpha)^2 Z_{t-2} + \cdots \\ &\quad\quad\quad\quad\quad\quad + \alpha (1 - \alpha)^{t-1} Z_1 + (1 - \alpha)^t P_1. \end{align*}\]
Los coeficientes \(\alpha, \alpha (1-\alpha)^2,..., \alpha (1-\alpha)^t\) decrecen exponencialmente.
El pronóstico \(P_{t+1}\) es un promedio ponderado de las observaciones pasadas \(Z_t,...,Z_1\) ya que \((1-\alpha)^t P_{1}\) es casi nulo.
En la práctica, \(\alpha\) es desconocido.
La idea es realizar SES con diferentes valores de \(\alpha\) y seleccionar el valor de \(\alpha\) que minimiza la suma de los cuadrados de los errores de pronóstico, o el MSE. \[\operatorname{MSE}=\frac{\sum\limits_{t=1}^T \left( Z_t-P_t \right)^2}{T}.\]
Además de \(\alpha\), la selección de los valores iniciales (\(P_1\)) es importante.
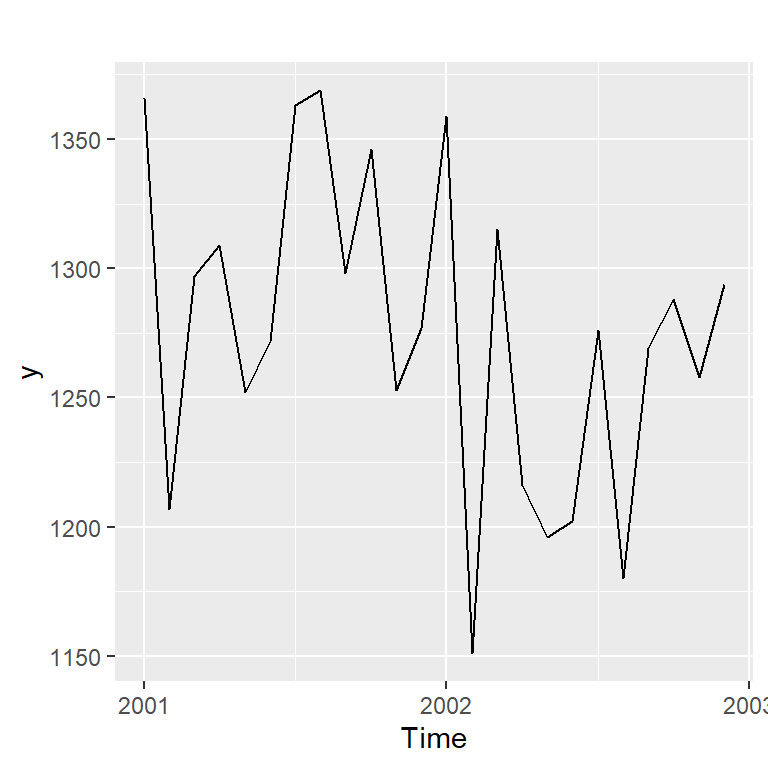
- Ejemplo 3.1 de Hernández (2011): Serie mensual de defunciones de Costa Rica de los años 2001 y 2002.
El método lineal de Holt
Contenido
Introducción
Suavizamiento exponencial simple (SES)
El método lineal de Holt
El método lineal de Holt amortiguado
El método multiplicativo y aditivo de Holt-Winters
Taxonomía de los métodos de SE
Representación como modelos de Espacio de Estados
El método lineal de Holt
- El método de Holt sirve para series con tendencia.
- El suavizamiento exponencial de Holt utiliza 3 ecuaciones y dos parámetros ( \(0 \leq \alpha \leq 1\) y \(0 \leq \beta \leq 1\)):
Ecuación del nivel: \(~~~~~~~~~~~~~l_{t}=\alpha Z_{t} + (1-\alpha)~ (l_{t-1}+b_{t-1})\)
Ecuación de la pendiente: \(~~~~b_{t}=\beta (l_t-l_{t-1}) + (1-\beta)~ b_{t-1}\)
Ecuación del pronóstico: \(~~~~~P_{t+m}=l_t+b_t m\)
\(l_t\) es una estimación del nivel promedio de \(Z_t\).
- Es un promedio ponderado del valor de \(Z_t\) y una estimación del nivel de la serie en \(t\).
\(b_t\) es una estimación de la pendiente de \(Z_t\).
- es un promedio ponderado del aumento del nivel de la serie entre \(t\) y \(t-1\), y una estimación de la pendiente en el tiempo \(t-1\).
La última ecuación pronostica el valor de \(Z_{t+m}\), i.e., pronóstico a \(m\) paso para adelante.
Es conocido como suavizamiento exponencial doble.
- Al igual que SES, los valores de \(\alpha\) y \(\beta\) se obtienen minimizando la suma de los cuadrados de los errores de pronóstico, o el MSE. \[\operatorname{MSE}=\frac{\sum\limits_{i=1}^T \left( Z_t-P_t \right)^2}{T} \]
- Además de \(\alpha\) y \(\beta\), la selección de los valores iniciales (\(l_1\) y \(b_1\)) es importante.
- Ejemplo 3.2 de Hernández (2011): Serie de graduados del ITCR de 1975-2002.
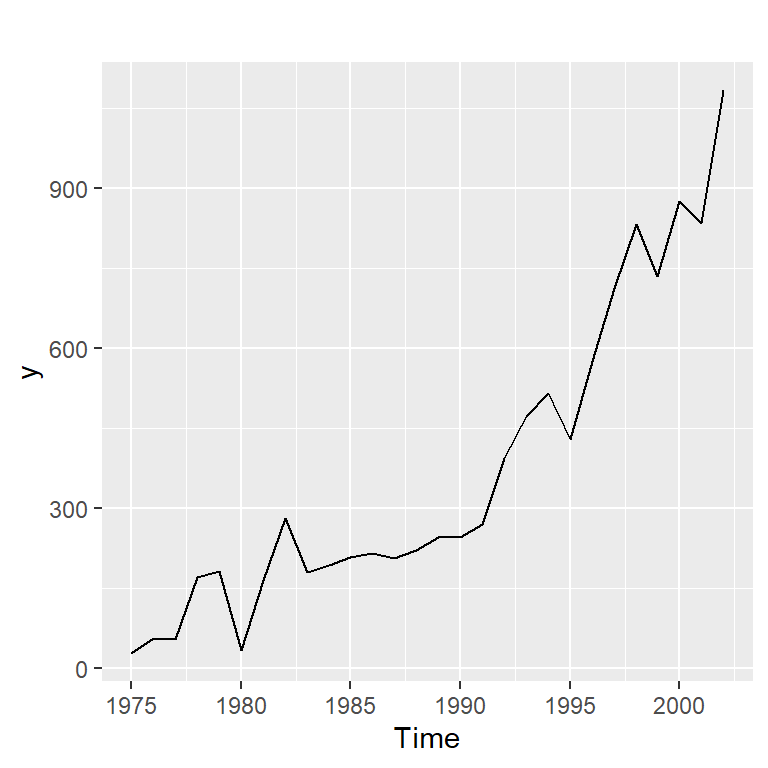
El método lineal de Holt amortiguado
Contenido
Introducción
Suavizamiento exponencial simple (SES)
El método lineal de Holt
El método lineal de Holt amortiguado
El método multiplicativo y aditivo de Holt-Winters
Taxonomía de los métodos de SE
Representación como modelos de Espacio de Estados
El método lineal de Holt amortiguado
- Crítica: el método lineal de Holt supone una tendencia constante a futuro.
- Pronósticos a largo plazo no son prácticos.
- Gardner & McKenzie (1985) introdujo un parámetro adicional para amortiguar esa tendencia constante.
Ecuación del nivel: \(~~~~~~~~~~~~~l_{t}=\alpha Z_{t} + (1-\alpha)~ (l_{t-1}+\phi b_{t-1})\)
Ecuación de la pendiente: \(~~~~b_{t}=\beta (l_t-l_{t-1}) + (1-\beta)~ \phi b_{t-1}\)
Ecuación del pronóstico: \(~~~~~P_{t+m}=l_t+ (\phi+\phi^2+...+\phi^m)~b_t\)
- Si \(\phi=1\), se tiene el método lineal de Holt.
- Para \(0<\phi<1\), el pronóstico converge a \(l_t+ \frac{\phi}{1-\phi}~b_t\), cuando \(m \rightarrow \infty\).
- Es decir, el pronóstico a corto plazo es con tendencia pero a largo plazo es constante.
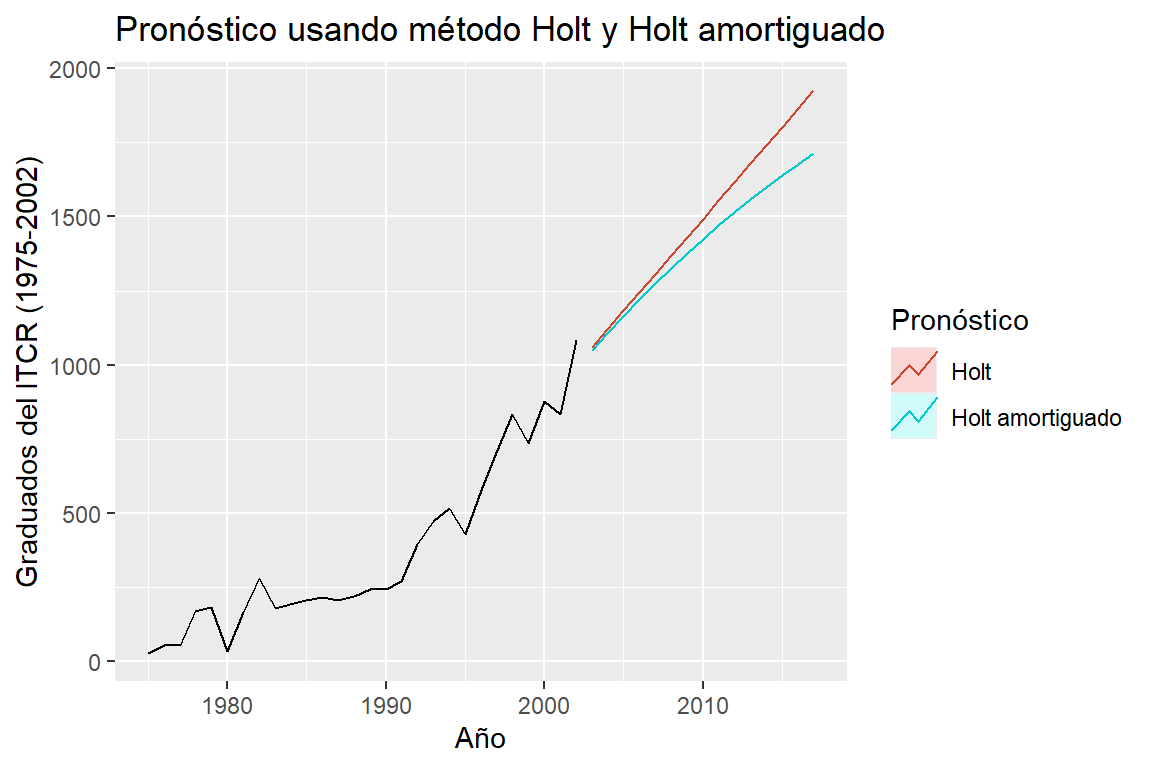
El método multiplicativo y aditivo de Holt-Winters
Contenido
Introducción
Suavizamiento exponencial simple (SES)
El método lineal de Holt
El método lineal de Holt amortiguado
El método multiplicativo y aditivo de Holt-Winters
Taxonomía de los métodos de SE
Representación como modelos de Espacio de Estados
El método multiplicativo y aditivo de Holt-Winters
Winters (1960) extendió el método lineal de Holt para tomar en cuenta la estacionalidad, el cual es conocido como Holt-Winters.
Método multiplicativo:
- Variación estacional cambia proporcionalmente con el nivel de la serie.
Método aditivo:
- Variación constante a lo largo de tiempo.
El método multiplicativo de Holt-Winters
\[l_t= \alpha \frac{Z_t}{S_{t-s}}+(1-\alpha) (l_{t-1}+b_{t-1})\] \[b_t= \beta (l_t-l_{t-1})+(1-\beta) b_{t-1}\] \[S_t= \gamma \frac{Z_t}{l_{t-1}+b_{t-1}}+(1-\gamma) S_{t-s}\] \[P_{t+m}= (l_{t}+b_t~m) S_{t+m-s}\] donde
\(s\) es la longitud de la estacionalidad,
\(l_t\) es el nivel de la serie \(Z_t\),
\(b_t\) es la tendencia,
\(S_t\) es el componente estacional,
\(P_{t+m}\) es el pronóstico \(m\) pasos adelante y
\(0<\alpha<1\), \(0<\beta<1\), \(0<\gamma<1\).
Valores iniciales: para \(s\) periodos,
El nivel \(l_t\) se inicia con: \[l_s=\frac{Z_1+...+Z_s}{s}\] como un promedio de los datos de los primeros \(s\) datos.
La pendiente \(b_t\) se inicia con: \[b_s=\frac{1}{s}\left[ \frac{Z_{s+1}-Z_1}{s}+\frac{Z_{s+2}-Z_2}{s}+...+\frac{Z_{s+s}-Z_s}{s} \right]\] \[=\frac{1}{s}\left[ \frac{Z_{s+1}+...+Z_{s+s}}{s}-\frac{Z_{1}+...+Z_{s}}{s} \right]\] como un promedio de pendientes de cada periodo en los primeros \(2s\) periodos.
Los índices estacionales se inicializan como cociente de los primeros \(s\) valores al promedio de los primeros \(s\) datos. \[S_i=\frac{Z_i}{l_s}, \text{ para } i=1,...,s\]
Ejemplo 3.3 de Hernández (2011): Serie mensual de turistas de 1991-2000.
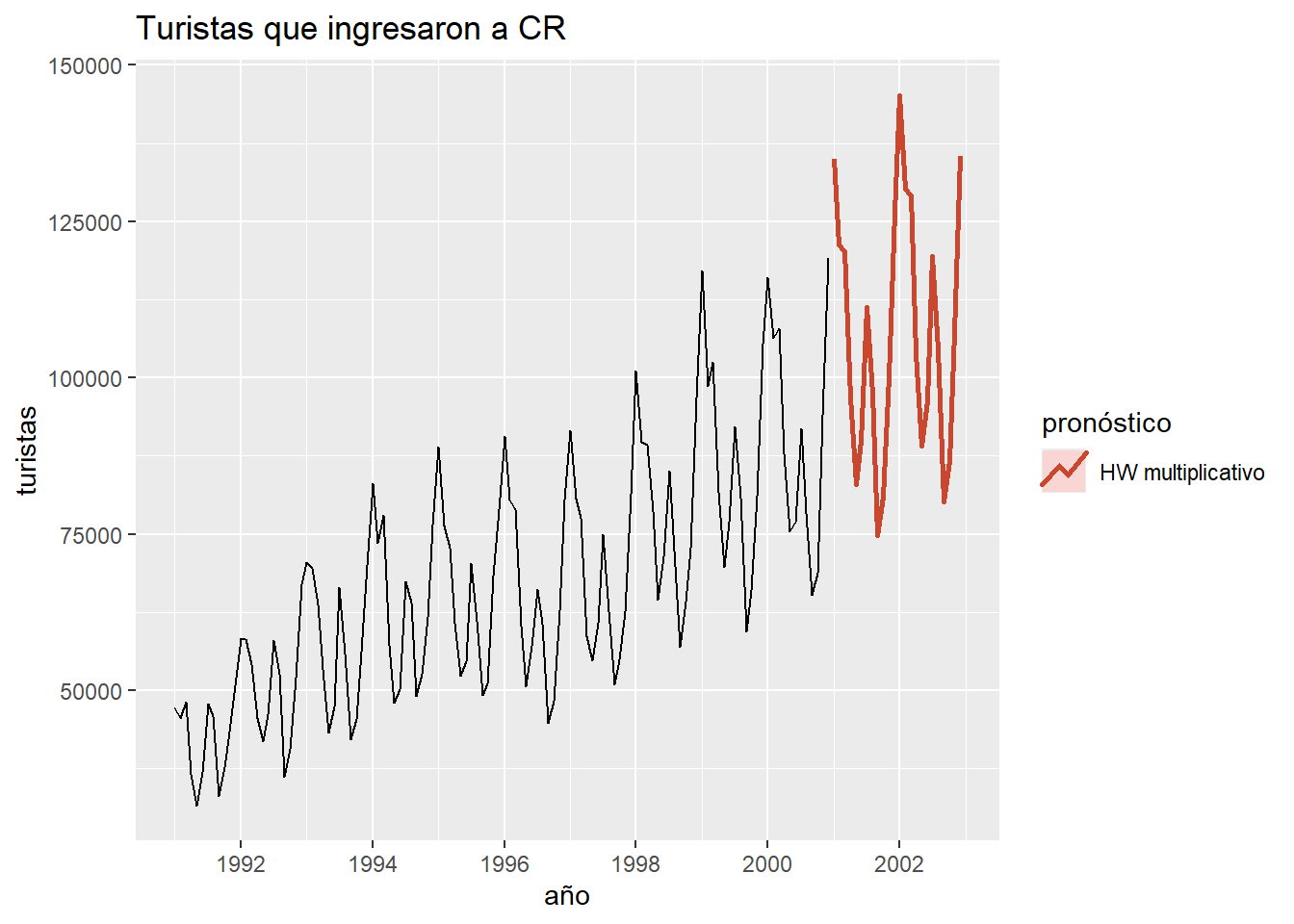
El método aditivo de Holt-Winters
\[l_t= \alpha (Z_t-S_{t-s})+(1-\alpha) (l_{t-1}+b_{t-1})\] \[b_t= \beta (l_t-l_{t-1})+(1-\beta) b_{t-1}\] \[S_t= \gamma \left( Z_t-l_{t-1}-b_{t-1} \right)+(1-\gamma) S_{t-s}\] \[P_{t+m}= l_{t}+b_t~m + S_{t+m-s}\] donde
\(s\) es la longitud de la estacionalidad,
\(l_t\) es el nivel de la serie \(Z_t\),
\(b_t\) es la tendencia,
\(S_t\) es el componente estacional,
\(P_{t+m}\) es el pronóstico \(m\) pasos adelante y
\(0<\alpha<1\), \(0<\beta<1\), \(0<\gamma<1\).
Los índices estacionales se inicializan como cociente de los primeros \(s\) valores al promedio de los primeros \(s\) datos. \[S_i=Z_i-a_s, \text{ para } i=1,...,s\]
Existen otras inicializaciones como el procedimiento basado en regresión (Bowerman, O’Connell and Koehler, 2005).
- asumir tendencia lineal de las primeras observaciones (típicamente 3 o 4 años), y usa el intercepto como \(l_0\) y pendiente como \(b_0\).
Hasta los últimos años siguen proponiendo nuevos métodos.
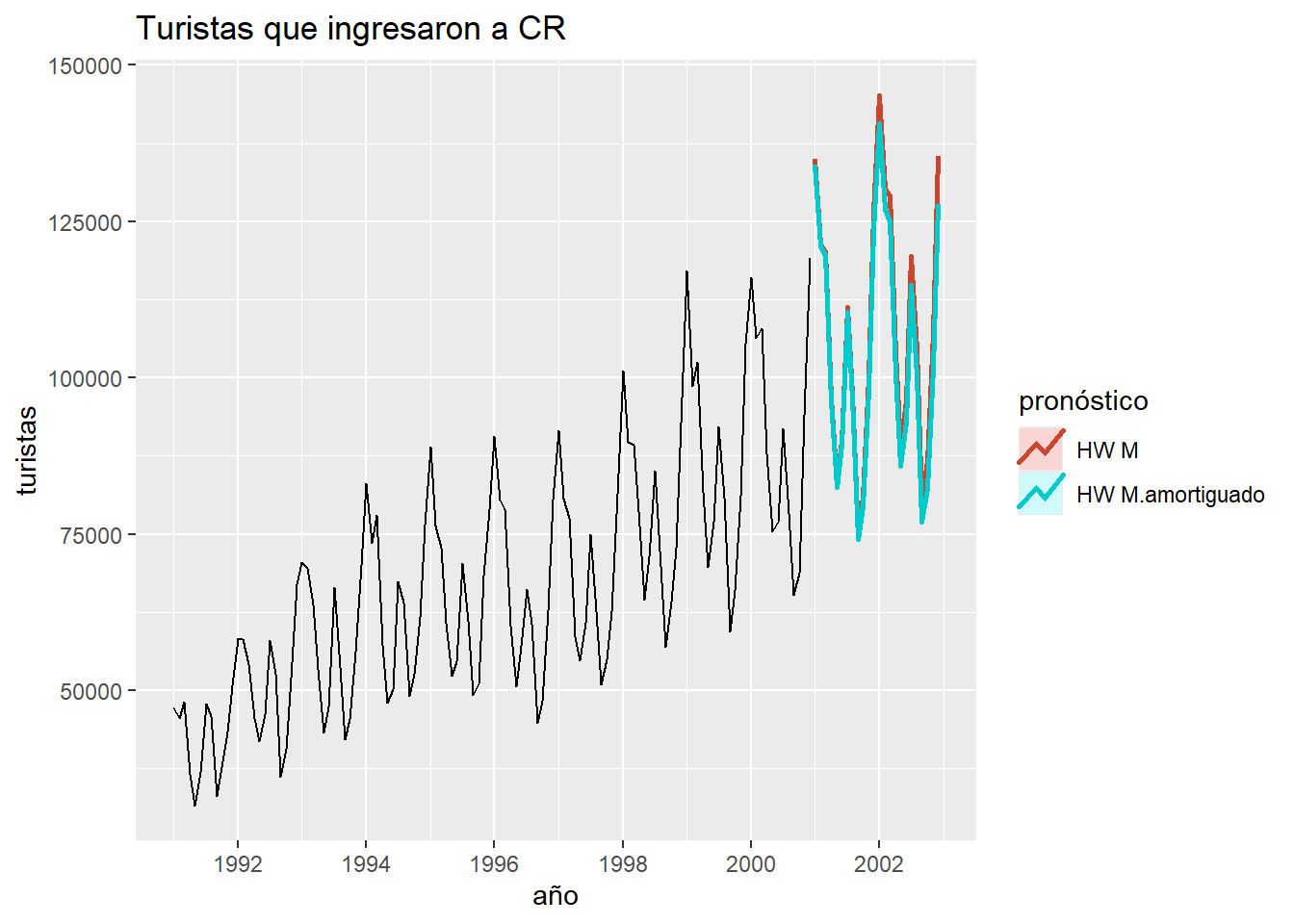
Comparación entre el aditivo y multiplicativo de H-W
ht1 <- hw(y,seasonal="multiplicative")
ht2 <- hw(y,seasonal="additive")
autoplot(y) +
autolayer(ht1, series="HW multiplicativo", PI=FALSE, size = 1) +
autolayer(ht2, series="HW aditivo", PI=FALSE, size = 1) +
xlab("año") +
ylab("turistas") +
ggtitle("Turistas que ingresaron a CR") +
guides(colour=guide_legend(title="pronóstico"))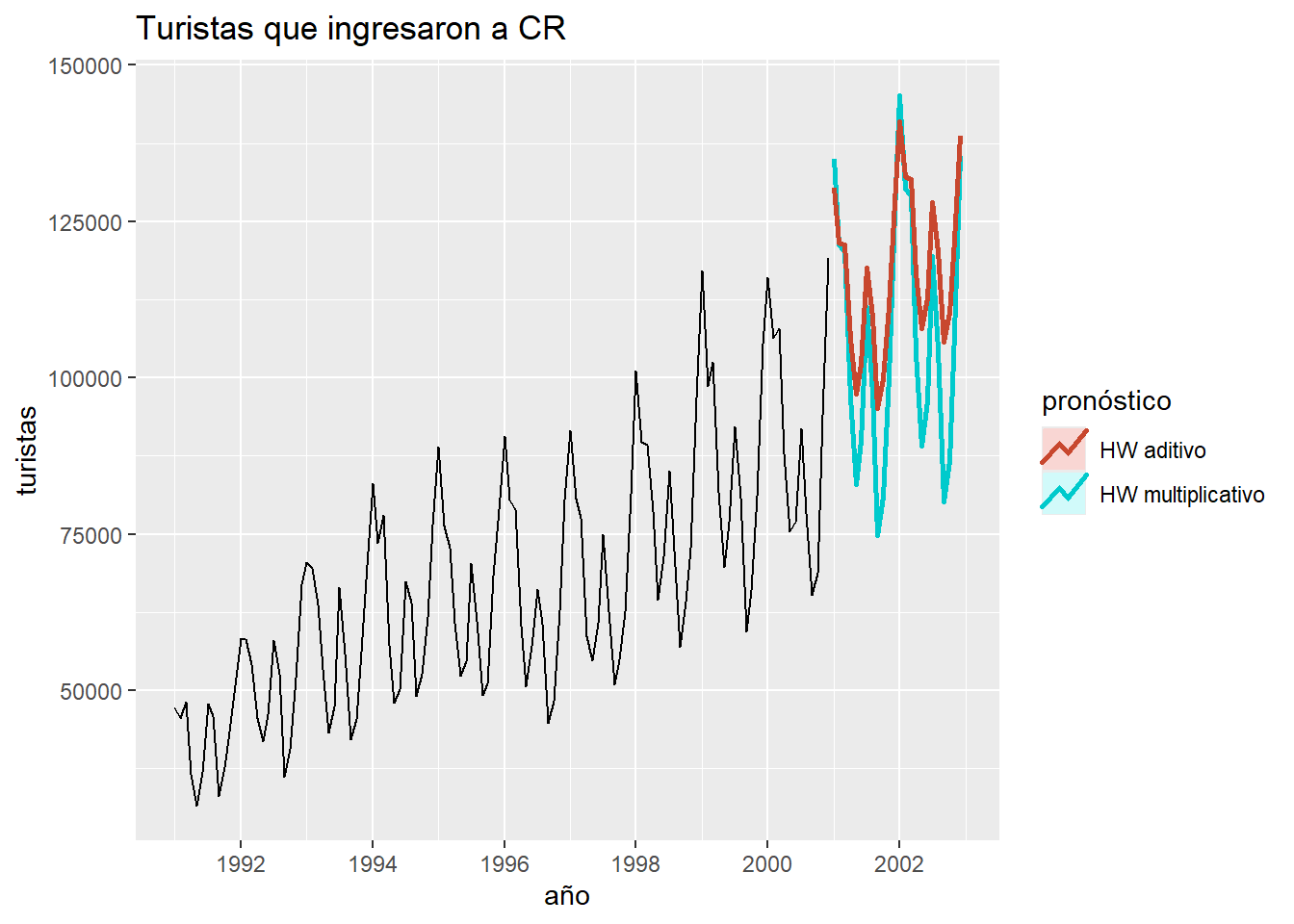
Comparación de las medidas de precisión.
El método mult. de H-W amortiguado
\[l_t= \alpha \frac{Z_t}{S_{t-s}}+(1-\alpha) (l_{t-1}+\phi~b_{t-1})\] \[b_t= \beta (l_t-l_{t-1})+(1-\beta)~\phi~ b_{t-1}\] \[S_t= \gamma \frac{Z_t}{l_{t-1}+\phi~b_{t-1}}+(1-\gamma) S_{t-s}\] \[P_{t+m}= (l_{t}+(\phi+\phi^2+...+\phi^m)~ b_t) S_{t+m-s}\]
Damped Holt-Winters' multiplicative method
Call:
hw(y = y, seasonal = "multiplicative", damped = TRUE)
Smoothing parameters:
alpha = 0.66
beta = 0.024
gamma = 1e-04
phi = 0.9684
Initial states:
l = 37734.1221
b = 789.7191
s = 1.1839 0.9441 0.7666 0.7176 0.939 1.0778
0.8739 0.8108 0.9503 1.1853 1.2078 1.3431
sigma: 0.0525
AIC AICc BIC
2539.896 2546.668 2590.071 ME RMSE MAE MPE MAPE MASE
Training set -114.3084 3239.923 2580.033 -0.3986991 3.995136 0.4245259
ACF1
Training set 0.008128625 ME RMSE MAE MPE MAPE MASE
Training set -394.643 4297.824 3312.546 -0.7003905 5.216058 0.5450557
ACF1
Training set -0.003603756 ME RMSE MAE MPE MAPE MASE
Training set 309.2038 3213.097 2587.598 0.2712205 3.958626 0.4257708
ACF1
Training set -0.01930739Taxonomía de los métodos de SE
Contenido
Introducción
Suavizamiento exponencial simple (SES)
El método lineal de Holt
El método lineal de Holt amortiguado
El método multiplicativo y aditivo de Holt-Winters
Taxonomía de los métodos de SE
Representación como modelos de Espacio de Estados
Taxonomía de los métodos de SE
| Tendencia | Componente estacional | ||
|---|---|---|---|
| \(N\) (No) | \(A\) (Aditivo) | \(M\) (Multiplicativo) | |
| \(N (\text{No)}\) | \((N,N)\) | \((N,A)\) | \((N,M)\) |
| \(A (\text{Aditivo})\) | \((A,N)\) | \((A,A)\) | \((A,M)\) |
| \(A_d\) \((\text{Aditivo}_{damped})\) | \((A_d,N)\) | \((A_d,A)\) | \((A_d,M)\) |
Note que algunos de estos ya lo acabamos de ver:
- \((N,N)\): SES
- \((A,N)\): Método lineal de Holt
- \((A_d,N)\): Holt amortiguado
- \((A,A)\): HW aditivo
- \((A,M)\): H-W Multiplicativo
- \((A_d,M)\): H-W multiplicativo amortiguado
- \((A_d,A)\): H-W aditivo amortiguado
En
R, especifica el tipo de error como “aditivo” o “multiplicativo”, y se usa la notación del modelo ETS como(ZZZ), donde las 3Z’s representan:- El error (“A”, “M”, “Z”),
- La tendencia (“N”,“A”,“M” or “Z”), y
- El componente estacional (“N”,“A”,“M” or “Z”).
- \(N:\) no, \(A:\) aditivo, \(M:\) multiplicativo y \(Z:\) automático.
- Por ejemplo, si necesito estimar
turistas<-read.csv("turistas.csv",sep=";")
y<-ts(turistas$turistas,start=c(1991,1),frequency=12)
hw_ad<-ets(y,model="AAA",damped = FALSE)
hw_ad_a<-ets(y,model="AAA",damped = TRUE)
hw_mul<-ets(y,model="MAM",damped = FALSE)
hw_mul_a<-ets(y,model="MAM",damped = TRUE)
hw_auto<-ets(y,model="ZZZ") #selecciona el mejor modelo usando AIC.
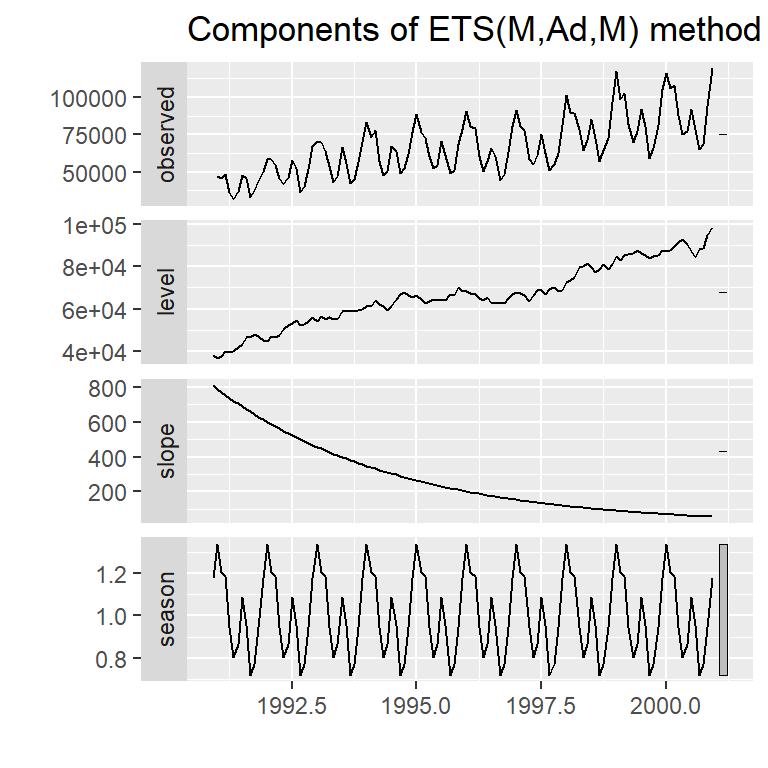
plot(hw_auto)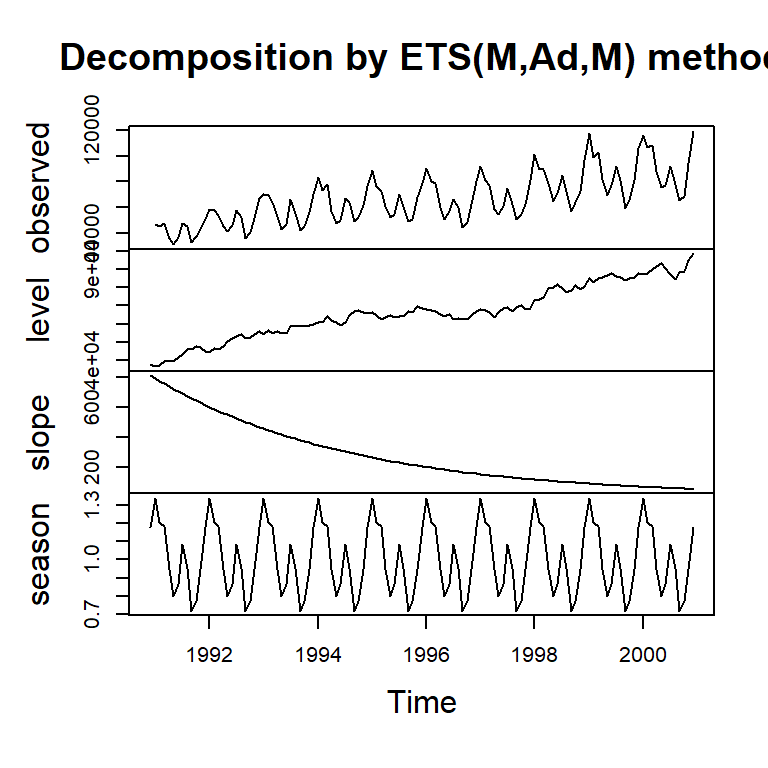
¿Qué es el término del error y cómo se define los criterios de información como el AIC?
Representación como modelos de Espacio de Estados
Contenido
Introducción
Suavizamiento exponencial simple (SES)
El método lineal de Holt
El método lineal de Holt amortiguado
El método multiplicativo y aditivo de Holt-Winters
Taxonomía de los métodos de SE
Representación como modelos de Espacio de Estados
Representación como modelos de Espacio de Estados
- El modelo de Espacio de Estados en general está caracterizado por dos procesos en el tiempo:
Un proceso latente (o oculto) \(x_t\): Se supone que es un proceso de Markov, i.e. \[P(x_t|x_{t-1},x_{t-2},...)=P(x_t|x_{t-1})\]
Un proceso de observaciones \(y_t\): Se supone que son independientes dado los estados \(x_t\).
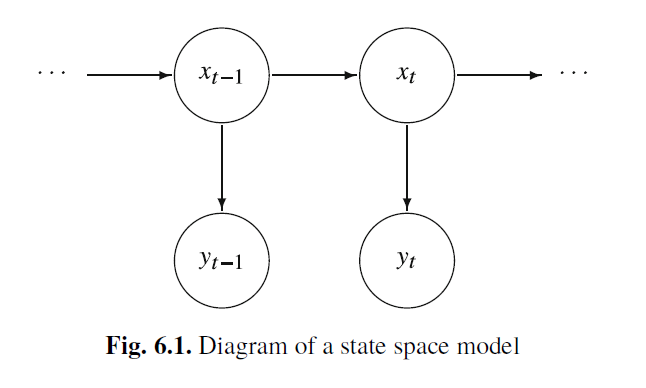
Fuente: Shumway & Stoffer (2017)
Representación del SES
Como ilustración, note que la ecuación del SES: \(P_{t+1}=\alpha Z_t + (1-\alpha)~ P_t\), se puede reescribir como:
- La ecuación del pronóstico:
\[\begin{align*}P_{t+1}=l_t \end{align*}\]
- La ecuación del suavizamiento:
\[\begin{align*} \ell_t &= \alpha Z_t + (1 - \alpha) P_t \\ &= \alpha Z_t + (1 - \alpha) \ell_{t-1} \end{align*}\]
Arreglando la ecuación del suavizamiento:
\[\begin{align*} \ell_t &= \ell_{t-1} + \alpha (Z_t - \ell_{t-1}) \\ &= \ell_{t-1} + \alpha e_t \end{align*}\]
donde \(e_t = Z_t - l_{t-1} = Z_t - P_{t}\) es el error.
Podríamos definir la ecuación del pronóstico como \(Z_t = l_{t-1}+e_t\), introduciendo un error aleatorio. Finalmente, la representación del modelo Espacio de Estados se escribe de la siguiente forma: \[\begin{align*} Z_t &= \ell_{t-1} + e_t \\ \ell_t &= \ell_{t-1} + \alpha e_t \end{align*}\]
Asumiendo alguna distribución de \(e_t\), se puede especificar el modelo estadístico. Por lo que se puede realizar inferencias a los parámetros y los pronósticos con intervalo de confianza.
De forma similar, el SES con el error multiplicativo es
\[\begin{align*} Z_t &= \ell_{t-1} ( 1+ e_t) \\ \ell_t &= \ell_{t-1} (1 + \alpha e_t) \end{align*}\]
Comparación de varios modelos
ME RMSE MAE MPE MAPE MASE
Training set -394.6563 4297.824 3312.536 -0.7004108 5.216048 0.5450541
ACF1
Training set -0.003568228 ME RMSE MAE MPE MAPE MASE ACF1
Training set 260.7423 4254.83 3302.818 0.2544367 5.10127 0.543455 0.00139745 ME RMSE MAE MPE MAPE MASE
Training set -296.167 3301.525 2602.353 -0.7057268 3.976193 0.4281986
ACF1
Training set 0.07227753 ME RMSE MAE MPE MAPE MASE ACF1
Training set 372.8259 3283.797 2633.531 0.3366449 3.939674 0.4333287 0.07885943 ME RMSE MAE MPE MAPE MASE ACF1
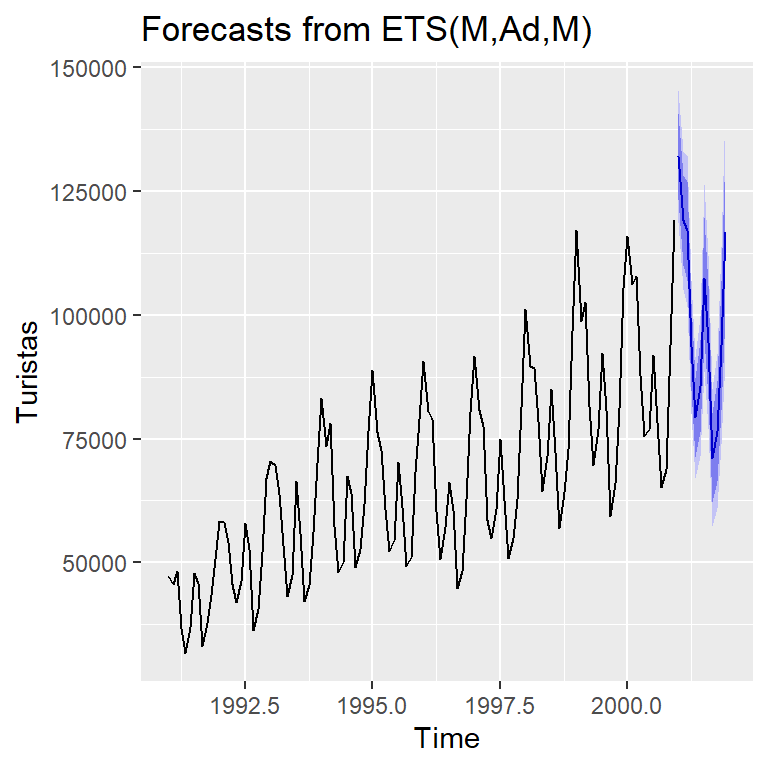
Training set 372.8259 3283.797 2633.531 0.3366449 3.939674 0.4333287 0.07885943ETS(M,Ad,M)
Call:
ets(y = y, model = "ZZZ")
Smoothing parameters:
alpha = 0.5798
beta = 1e-04
gamma = 1e-04
phi = 0.9774
Initial states:
l = 37996.857
b = 809.5089
s = 1.1769 0.9461 0.7722 0.7183 0.955 1.0858
0.8657 0.8016 0.9472 1.1851 1.2074 1.3387
sigma: 0.0516
AIC AICc BIC
2535.688 2542.460 2585.863
Training set error measures:
ME RMSE MAE MPE MAPE MASE ACF1
Training set 372.8259 3283.797 2633.531 0.3366449 3.939674 0.4333287 0.07885943