Tema 4: Regresión con series de tiempo
Paquetes de R
Para este tema, se necesita cargar estos paquetes:
Introducción
Contenido
Introducción
Modelos de regresión
Regresión espuria
El tiempo como covariables
Pronósticos usando regresión
Extensiones de modelos de regresión
Introducción
La idea es ajustar un modelo de regresión para la serie temporal \(Y_t, t=1,...,T\) utlizando un conjunto de \(p\) covariables: \(X_1,...,X_p\).
Por ejemplo:
- \(Y\) una serie mensual de ventas con la variable independiente \(X_1\) gasto mensual en anuncios.
- \(Y\) una serie diaria de demanda de energía eléctrica con las variables independientes: \(X_1\) temperatura y \(X_2\) el día de la semana.
Modelos de regresión
Contenido
Introducción
Modelos de regresión
Regresión espuria
El tiempo como covariables
Pronósticos usando regresión
Extensiones de modelos de regresión
Regresión lineal simple
Un modelo de regresión lineal simple establece una relación lineal entre una variable dependiente \(Y\) y una sola variable predictora \(X\):
\[
Y_t = \beta_0 + \beta_1 X_t + \epsilon_t,
\] donde los coeficientes \(\beta_0\) y \(\beta_1\) denotan la intersección y la pendientes, respectivamente;
\(\varepsilon_t \overset{\text{iid}}{\sim} N(0,\sigma^2)\).
- La intercepción \(\beta_0\) representa el valor predicho de \(y\) cuando \(X=0\).
- La pendiente \(\beta_1\) representa el cambio promedio previsto en \(Y\) resultante de un aumento de una unidad en \(X\).
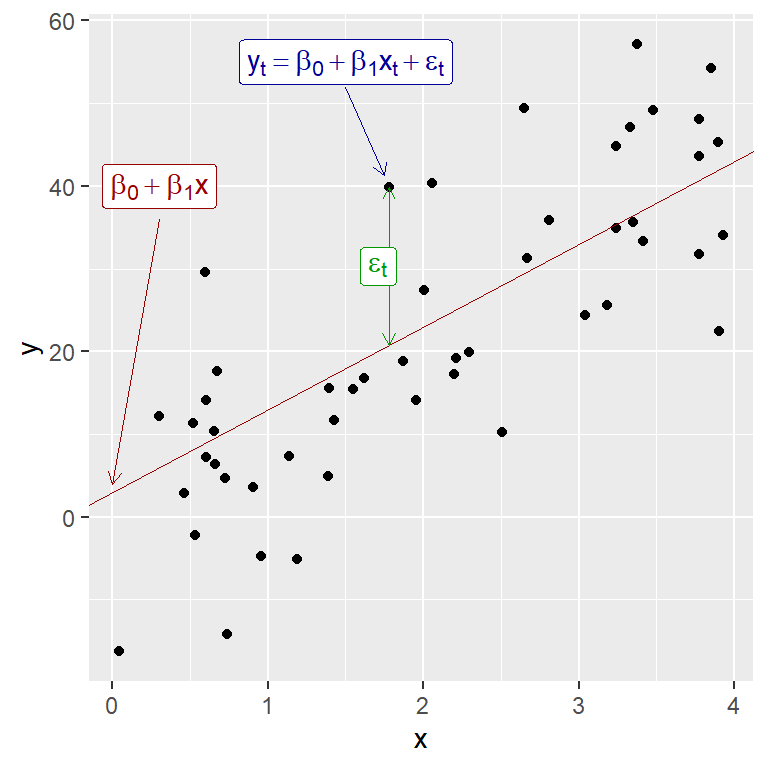
Ejemplo simulado de un modelo de regresión lineal simple (Fig 5.1 de Hyndman)
Ejemplo
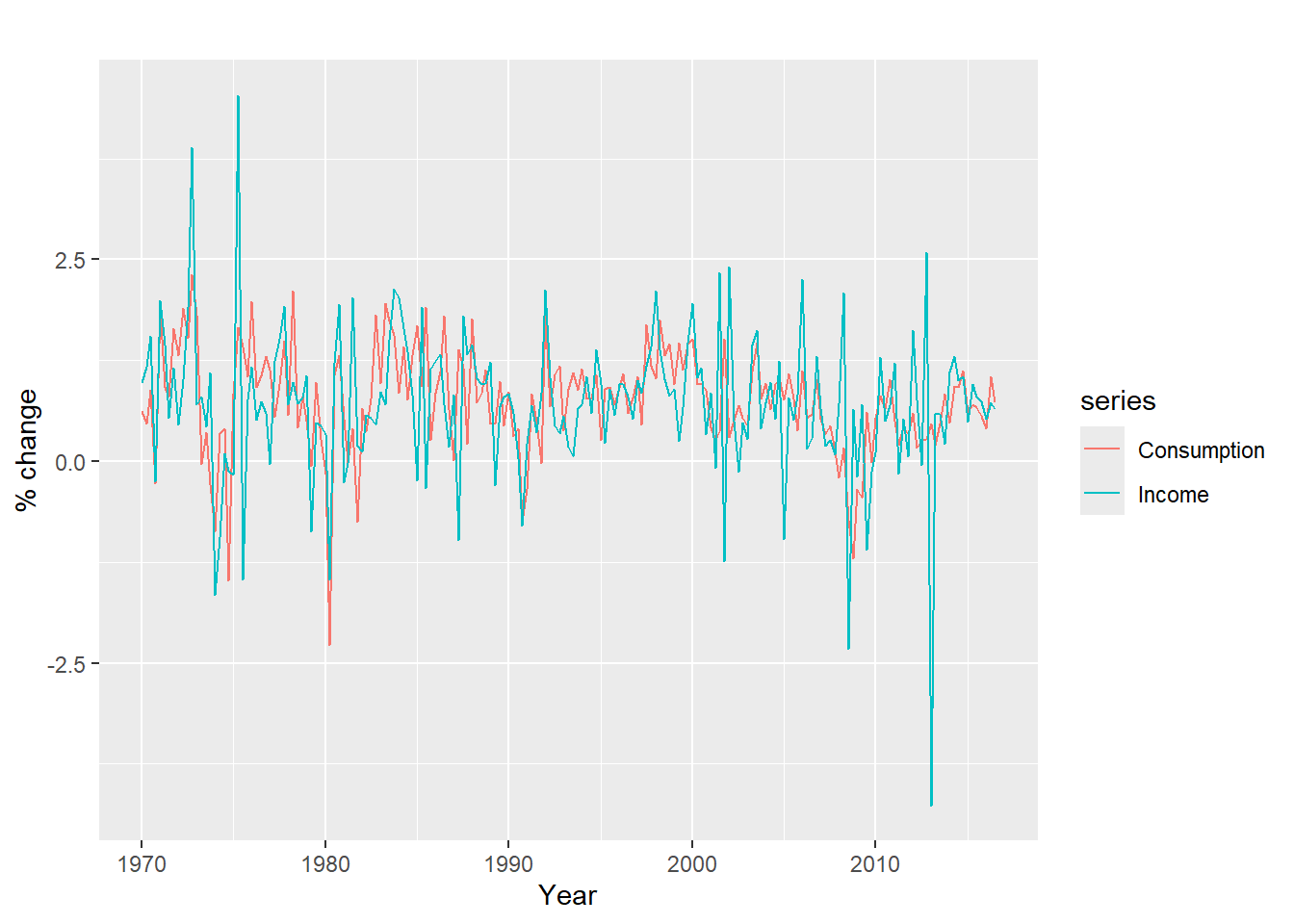
- La serie de cambios porcentuales trimestrales (tasas de crecimiento) del gasto de consumo personal real (\(Y_t\), variable dependiente), y el cambio porcentual de los ingresos disponibles(\(X_t\), covariable), para EE.UU. desde 1970 a 2016.
Consumption Income Production Savings Unemployment
1970 Q1 0.6159862 0.9722610 -2.4527003 4.8103115 0.9
1970 Q2 0.4603757 1.1690847 -0.5515251 7.2879923 0.5
1970 Q3 0.8767914 1.5532705 -0.3587079 7.2890131 0.5
1970 Q4 -0.2742451 -0.2552724 -2.1854549 0.9852296 0.7
1971 Q1 1.8973708 1.9871536 1.9097341 3.6577706 -0.1
1971 Q2 0.9119929 1.4473342 0.9015358 6.0513418 -0.1uschange %>%
as.data.frame() %>%
ggplot(aes(x=Income, y=Consumption)) +
ylab("Consumption (quarterly % change)") +
xlab("Income (quarterly % change)") +
geom_point() +
geom_smooth(method="lm", se=FALSE)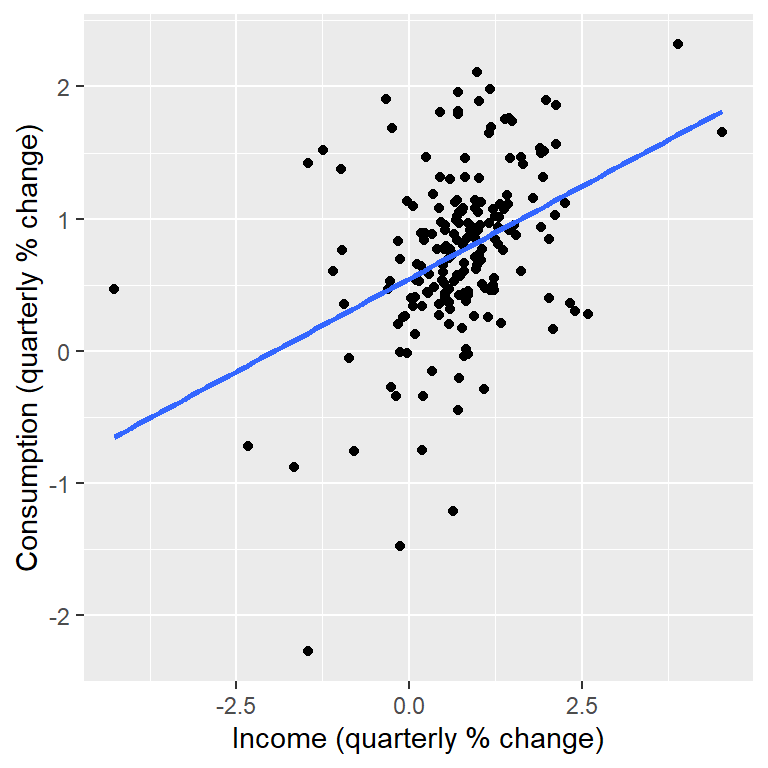
- Más adelante vemos que
tslmes programado para series temporales, pero el cálculo es lo mismo.
Call:
lm(formula = Consumption ~ Income, data = uschange)
Coefficients:
(Intercept) Income
0.5451 0.2806
Call:
tslm(formula = Consumption ~ Income, data = uschange)
Coefficients:
(Intercept) Income
0.5451 0.2806 \[Y_t=0.55 + 0.28X_t + \epsilon_t\]
- El coeficiente de pendiente muestra que un aumento de una unidad en \(X\)(un aumento de 1 punto porcentual en el ingreso personal disponible) resulta en un promedio de 0.28 unidades de aumento en \(Y\).
Regresión lineal múltiple
- La forma general de un modelo de regresión lineal múltiple es:
\[Y_t=\beta_0+\beta_1 X_{t,1}+\beta_2 X_{t,2}+...+\beta_p X_{t,p}+\epsilon_t, t=1,...,T,\]
donde \(Y_t\) es la variable a pronosticar y \(X_1,...,X_p\) son los \(p\) variables predictoras. Las variables predictoras pueden ser numéricas o categóricas (con el manejo apropiado de factores).
Los coeficientes \(\beta_1,...,\beta_p\) miden el efecto de cada predictor después de tener en cuenta los efectos de todos los demás predictores del modelo. Por lo tanto, los coeficientes miden los efectos marginales de las variables predictoras.
- El modelo de regresión lineal múltiple en su forma matricial:
\[ Y=X \beta+\epsilon \] donde
\[Y=\left[ \begin{array}{c}Y_1 \\ \vdots \\Y_T \end{array} \right],~~ X= \left(\begin{array}{ccccc} 1& X_{11}& X_{12} & ... & X_{1p}\\ 1 & X_{21}& X_{22} & ... &X_{2p}\\ \vdots& \vdots & \ddots &\vdots& \vdots\\ 1& X_{T1}& X_{T2} & ... &X_{Tp} \end{array}\right),\] \[\beta=\left[ \begin{array}{c}\beta_0 \\ \vdots \\\beta_T \end{array} \right],~~\epsilon=\left[ \begin{array}{c}\epsilon_1 \\ \vdots \\\epsilon_T \end{array} \right].\]
Supocisiones del modelo:
La relación entre la variable de pronóstico y las variables predictoras satisface esta ecuación lineal.
Los errores \(\varepsilon_1,...,\varepsilon_T\):
- tienen media cero,
- no están autocorrelacionados,
- no están relacionados con las variables predictoras
Los errores se distribuyan normalmente con una varianza constante \(\sigma^2\).
Cada predictor \(X_i, i=1,...,p\) supone que es observado y fijo, i.e. no es una variable aleatoria.
Tópicos importantes:
- Estimación:
- Por mínimos cuadrados.
- Por máxima verosimilitud.
- Selección de variables
- Diagnósticos
- Medidas remediales
Estimación por mínimos cuadrados: minimizar \[\sum_{t=1}^T \epsilon_t^2=\sum_{t=1}^T [y_t-(\beta_0+\beta_1 x_{1,t}+...+\beta_k x_{k,t})]^2,\] en función de \(\beta_0,...\beta_k\).
Como resultado: \[\hat{\beta}=(X^\top X)^{-1}X^\top Y.\]
El estimador de máxima verosimilitud es equivalente.
Ejemplo
- El objetivo es generar pronósticos del consumo más precisos usando otros predictores, además del ingreso personal.
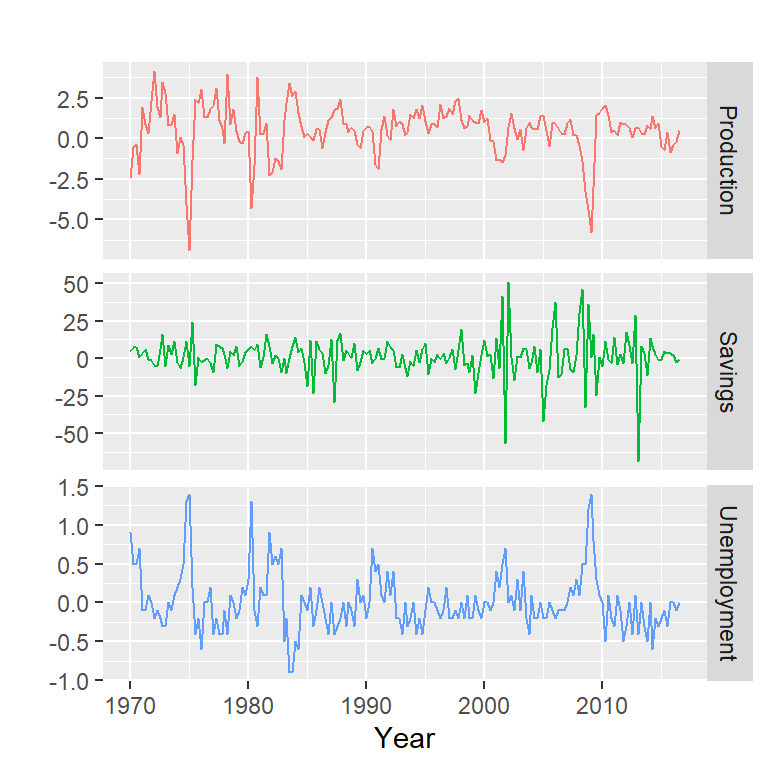
Variaciones porcentuales trimestrales en la producción industrial y ahorros personales y variaciones trimestrales en la tasa de desempleo de los EE. UU. Durante el período 1970T1-2016T3 (Hyndman)
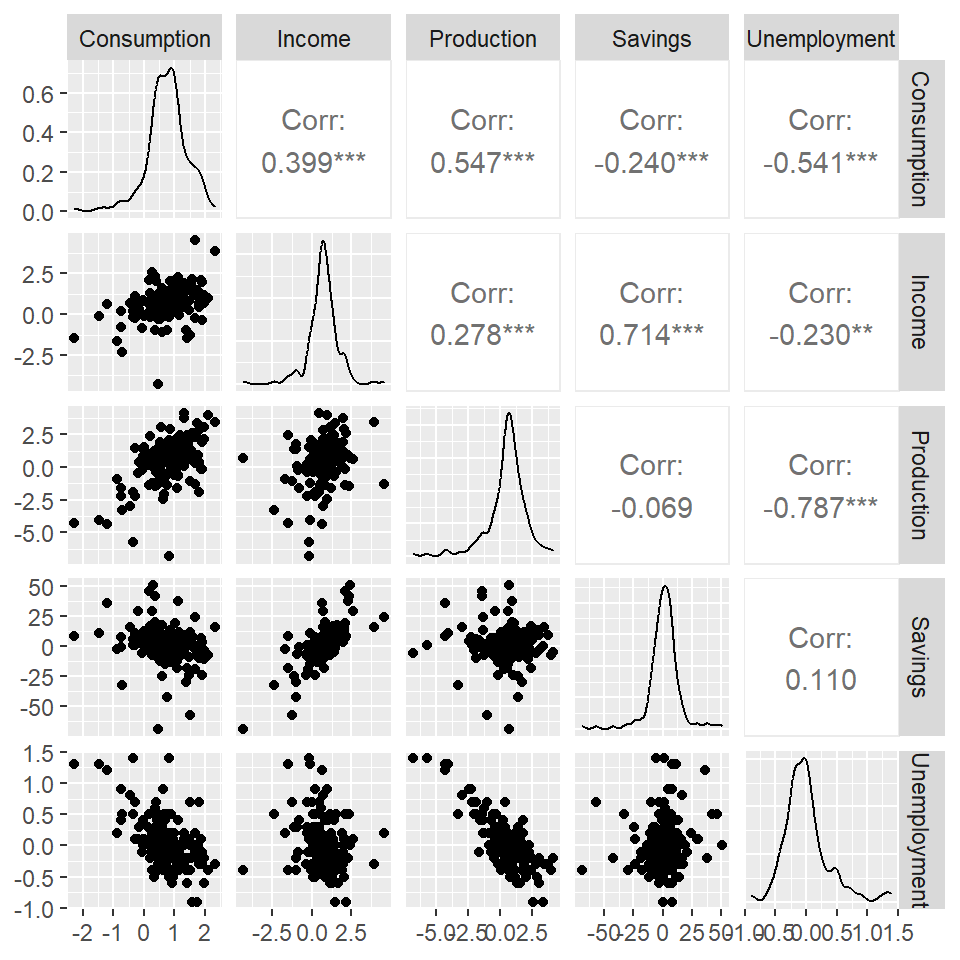
Matriz de diagrama de dispersión del gasto de consumo de EE. UU. y los cuatro predictores.
modreg <- tslm(
Consumption ~ Income + Production + Unemployment + Savings,
data=uschange)
summary(modreg)
Call:
tslm(formula = Consumption ~ Income + Production + Unemployment +
Savings, data = uschange)
Residuals:
Min 1Q Median 3Q Max
-0.88296 -0.17638 -0.03679 0.15251 1.20553
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 0.26729 0.03721 7.184 1.68e-11 ***
Income 0.71449 0.04219 16.934 < 2e-16 ***
Production 0.04589 0.02588 1.773 0.0778 .
Unemployment -0.20477 0.10550 -1.941 0.0538 .
Savings -0.04527 0.00278 -16.287 < 2e-16 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 0.3286 on 182 degrees of freedom
Multiple R-squared: 0.754, Adjusted R-squared: 0.7486
F-statistic: 139.5 on 4 and 182 DF, p-value: < 2.2e-16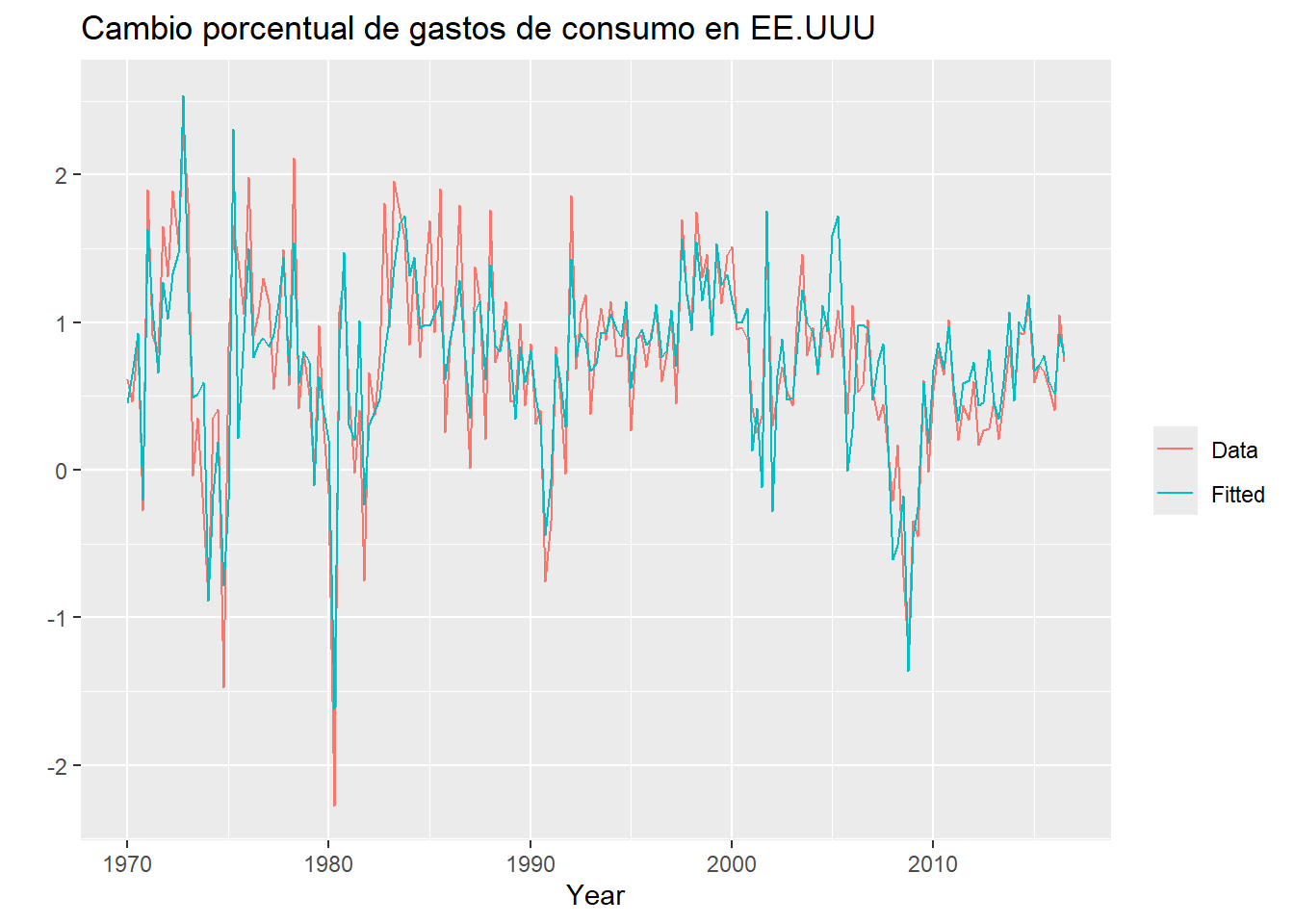
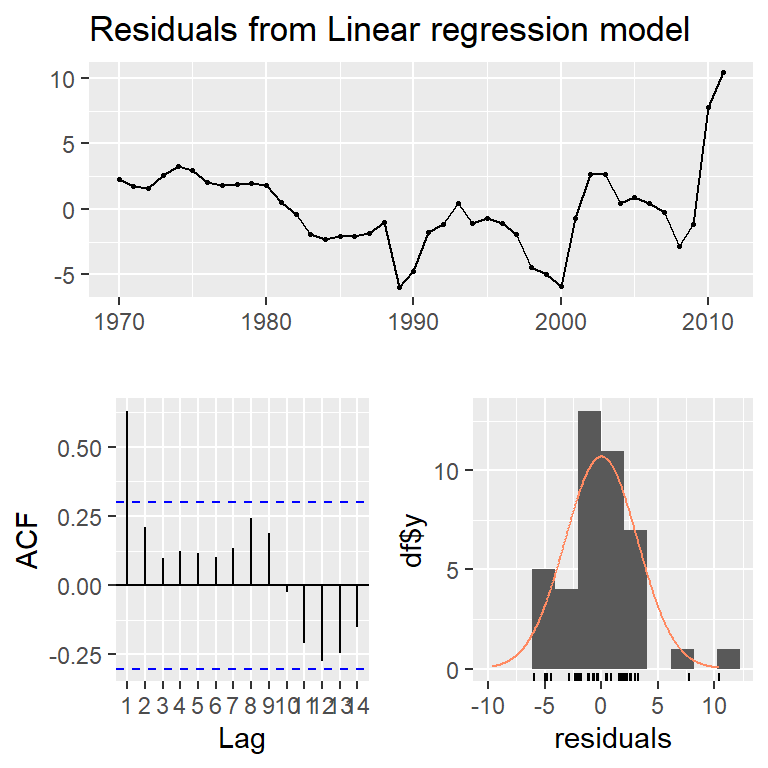
Breusch-Godfrey test for serial correlation of order up to 8
data: Residuals from Linear regression model
LM test = 14.874, df = 8, p-value = 0.06163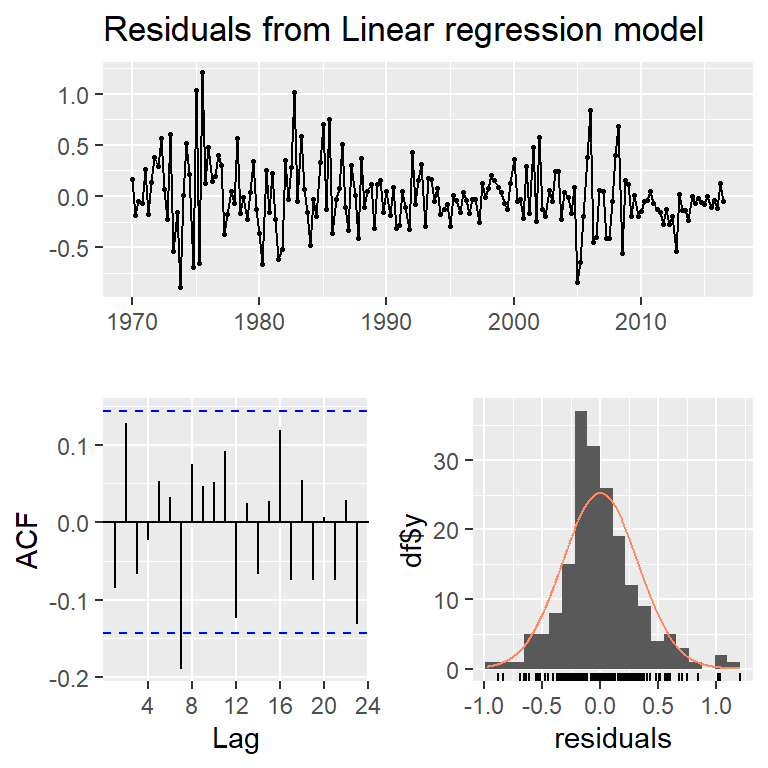
Regresión espuria
Contenido
Introducción
Modelos de regresión
Regresión espuria
El tiempo como covariables
Pronósticos usando regresión
Extensiones de modelos de regresión
Regresión espuria
- Cuando las series no son estacionarias1, los resultados de regresión no son confiables y presenta lo que se llama correlación espuria.
Los datos de las series cronológicas de tendencias pueden parecer relacionados.
Por ejemplo, los pasajeros aéreos en Australia tienen una correlación positiva con la producción de arroz en Guinea.
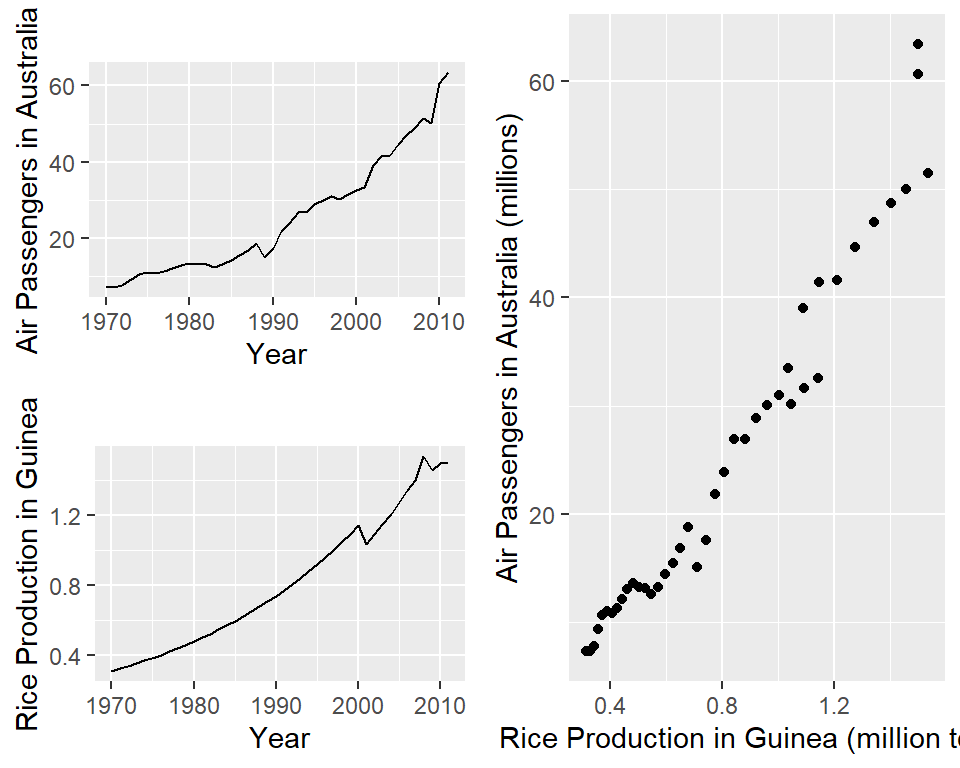
Call:
tslm(formula = aussies ~ guinearice)
Residuals:
Min 1Q Median 3Q Max
-5.9448 -1.8917 -0.3272 1.8620 10.4210
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) -7.493 1.203 -6.229 2.25e-07 ***
guinearice 40.288 1.337 30.135 < 2e-16 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 3.239 on 40 degrees of freedom
Multiple R-squared: 0.9578, Adjusted R-squared: 0.9568
F-statistic: 908.1 on 1 and 40 DF, p-value: < 2.2e-16El tiempo como covariables
Contenido
Introducción
Modelos de regresión
Regresión espuria
El tiempo como covariables
Pronósticos usando regresión
Extensiones de modelos de regresión
El tiempo como covariables
El tiempo también sirve como variable predictora:
- Modelos de tendencia (lineales o no lineales)
- Modelos estacionalidad (variables indicadoras)
Veremos más adelante en regresión dinámica:
- Análisis de intervención.
- Estrategias para valores extremos.
Modelos de tendencia
Como las variables independiente son asumidas como fijas, se puede utilizar el tiempo como una variable independiente.
Los modelos más frecuentes:
- Tendencia lineal: \[Y_t=\beta_0+\beta_1 t + \epsilon_t\]
- Tendencia cuadrática: \[Y_t=\beta_0+\beta_1 t +\beta_2 t^2 + \epsilon_t\]
Regresión no lineal.
- Por ejemplo: LOESS.
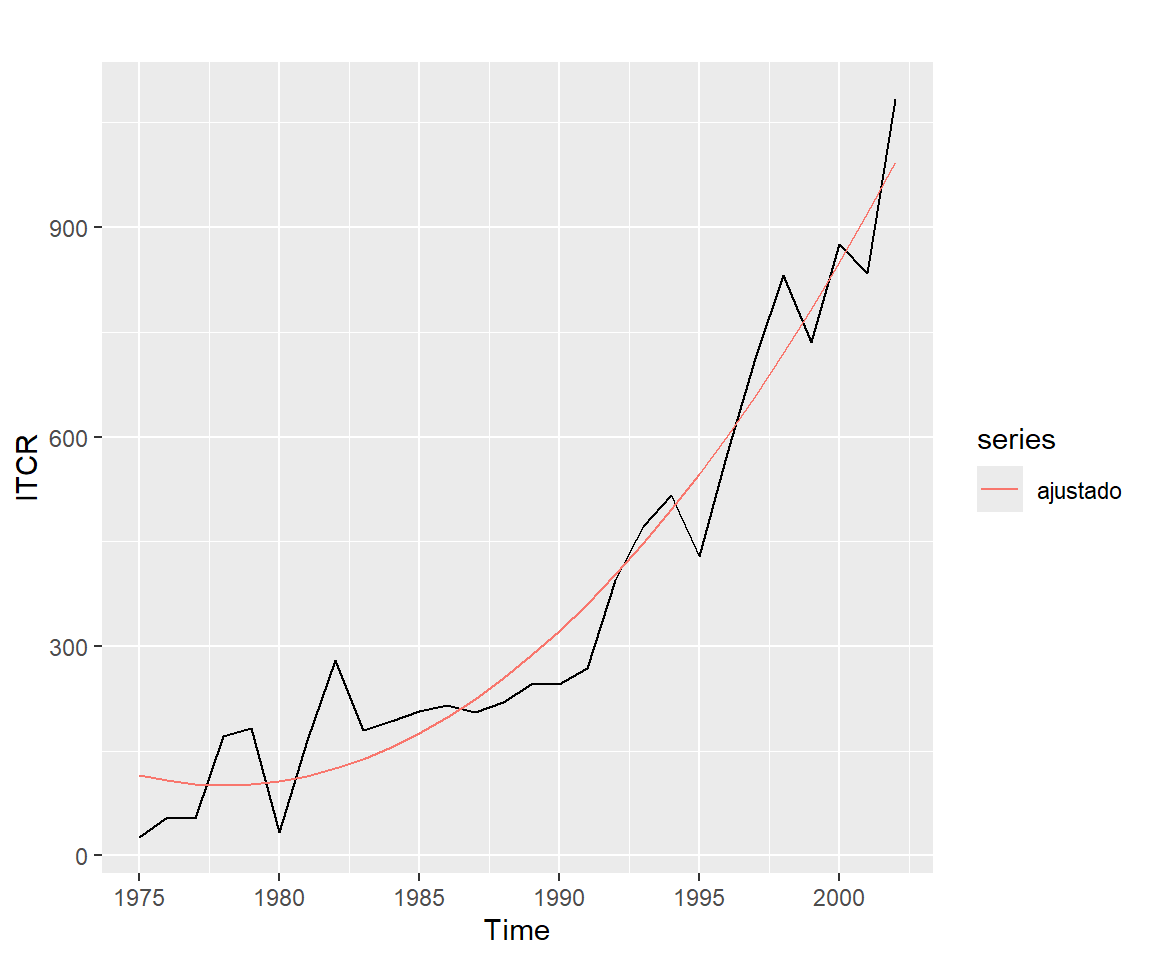
Vamos a ajustar un modelo de tendencia cuadrática a la serie de graduados de ITCR de 1975 a 2002: \[Y_t=\beta_0+\beta_1 t +\beta_2 t^2 + \epsilon_t, t=1,...,T\]
Call:
lm(formula = y ~ tiempo + tiempo2)
Residuals:
Min 1Q Median 3Q Max
-117.932 -49.683 4.506 43.234 155.390
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 127.0021 43.6818 2.907 0.00753 **
tiempo -12.7887 6.9427 -1.842 0.07736 .
tiempo2 1.5612 0.2323 6.720 4.83e-07 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 71.61 on 25 degrees of freedom
Multiple R-squared: 0.944, Adjusted R-squared: 0.9395
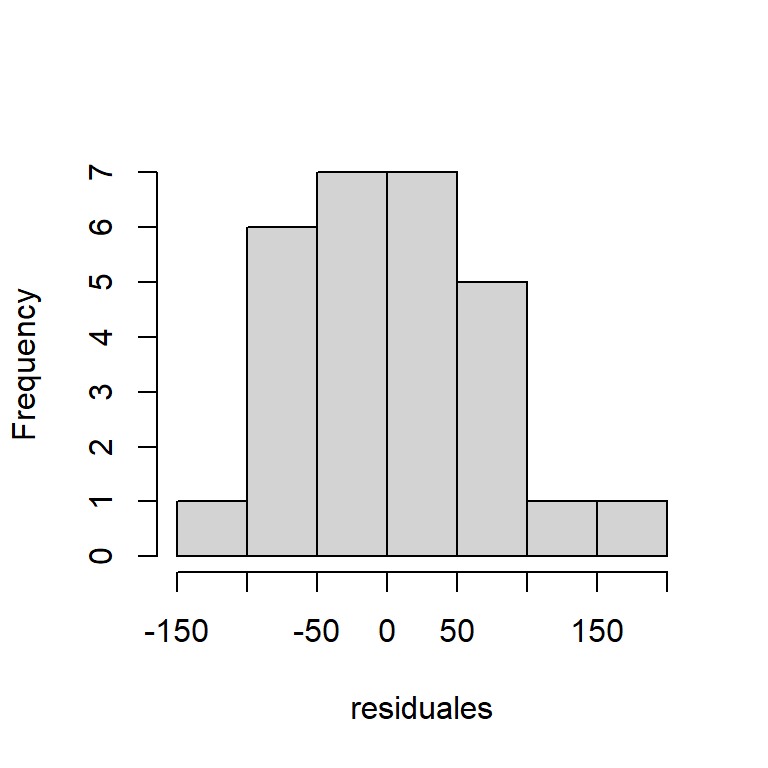
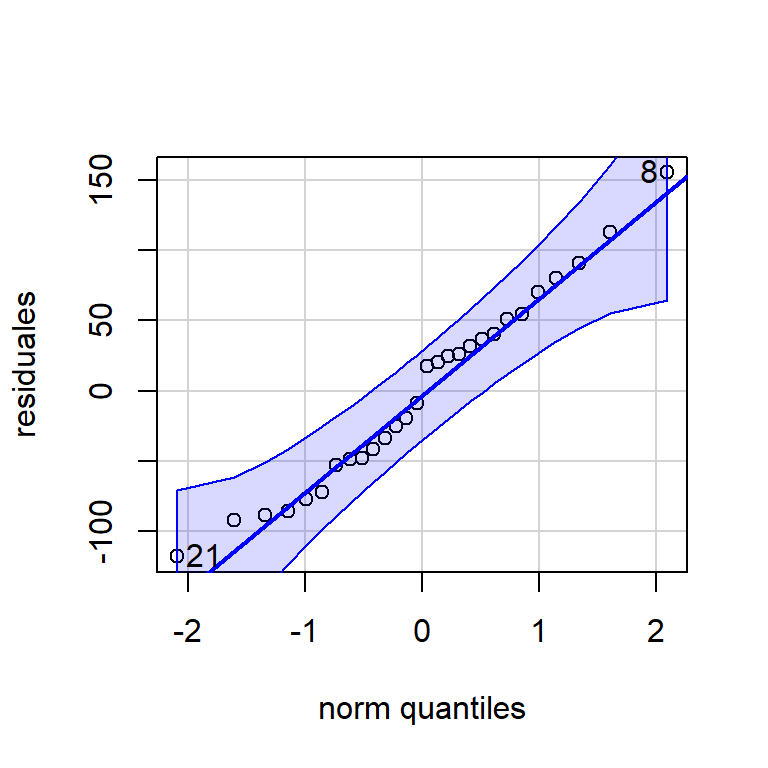
F-statistic: 210.6 on 2 and 25 DF, p-value: 2.268e-16- Los residuales en el tiempo:
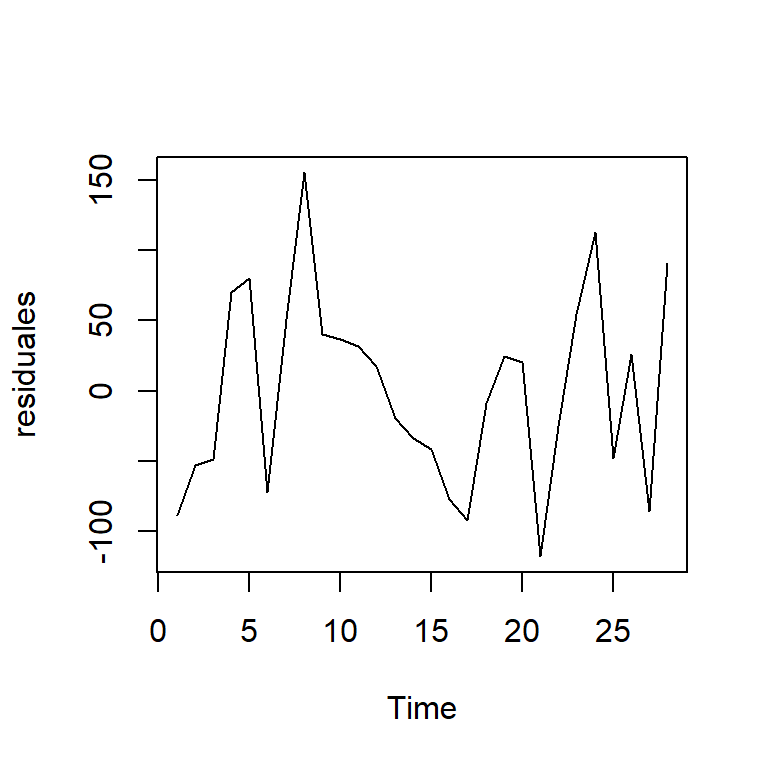
Breusch-Godfrey test for serial correlation of order up to 6
data: Residuals
LM test = 3.9215, df = 6, p-value = 0.6873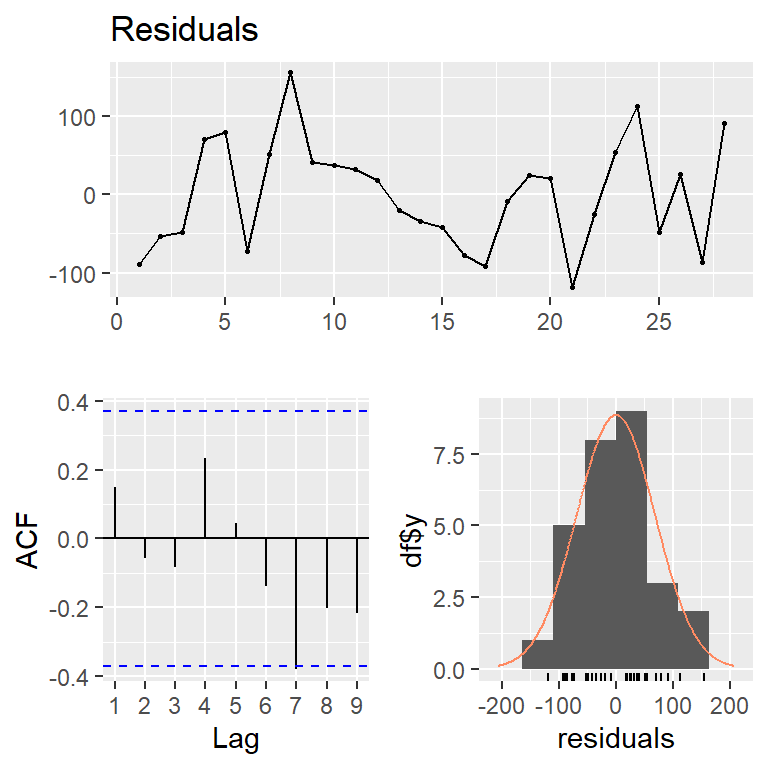
Transformación en modelos estacionales
- Si la magnitud del cambio estacional se mantiene aproximadamente constante con el cambio del nivel de la serie, se dice que la variación estacional es constante (aditiva).
- Si la variación estacional aumenta proporcionalmente con el nivel de la serie, se dice que la variación estacional es multiplicativa.
Transformaciones usadas en la práctica:
\(W_t=Y_t^\alpha,~~\text{con} -1<\alpha<1\)
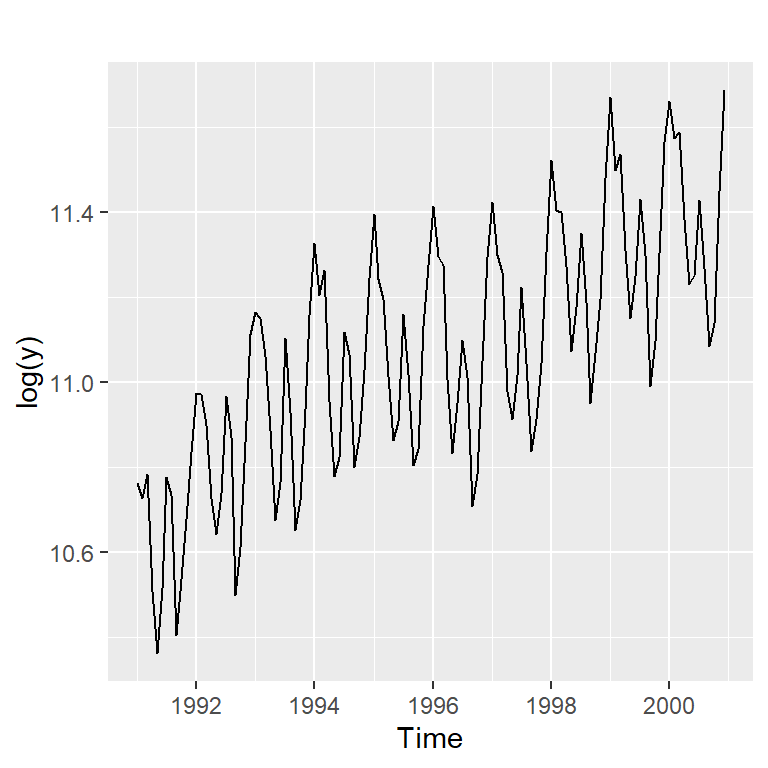
\(W_t=\ln Y_t\)
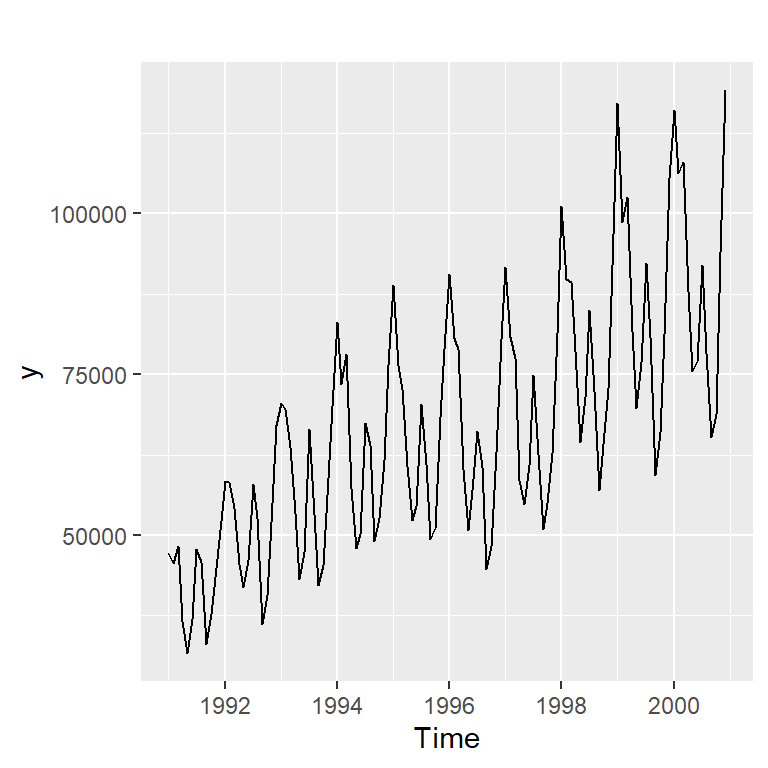
Ejemplo de turistas
Modelos de series estacionales mediante variables indicadoras
- La idea es utilizar un factor (variables indicadoras) como predictor para indicar el periodo de la estacionalidad.
- Ejemplo de turistas (datos mensuales y con tendencia cuadrática)
\[ln Y_t=\alpha_0+\alpha_1 t + \alpha_2 t^2 +\beta_1 I_{1}+...+\beta_11 I_{11}+\epsilon_t\]
w tiempo tiempo2 mes
1 10.76223 1 1 1
2 10.72731 2 4 2
3 10.78324 3 9 3
4 10.50832 4 16 4
5 10.36113 5 25 5
6 10.51486 6 36 6 w tiempo tiempo2 mes
115 11.42852 115 13225 7
116 11.26863 116 13456 8
117 11.08610 117 13689 9
118 11.13942 118 13924 10
119 11.45100 119 14161 11
120 11.68831 120 14400 12 Estimate Std. Error t value Pr(>|t|)
(Intercept) 10.9420 0.0294 372.1819 0.0000
tiempo 0.0086 0.0008 11.1807 0.0000
tiempo2 0.0000 0.0000 -3.2291 0.0017
mes2 -0.1013 0.0324 -3.1246 0.0023
mes3 -0.1181 0.0324 -3.6408 0.0004
mes4 -0.3467 0.0324 -10.6900 0.0000
mes5 -0.5050 0.0324 -15.5680 0.0000
mes6 -0.4243 0.0324 -13.0771 0.0000
mes7 -0.2037 0.0325 -6.2784 0.0000
mes8 -0.3326 0.0325 -10.2482 0.0000
mes9 -0.6091 0.0325 -18.7601 0.0000
mes10 -0.5293 0.0325 -16.2990 0.0000
mes11 -0.3263 0.0325 -10.0431 0.0000
mes12 -0.1042 0.0325 -3.2068 0.0018 Estimate Std. Error t value Pr(>|t|)
(Intercept) 10.9420 0.0294 372.1819 0.0000
trend 0.0086 0.0008 11.1807 0.0000
I(trend^2) 0.0000 0.0000 -3.2291 0.0017
season2 -0.1013 0.0324 -3.1246 0.0023
season3 -0.1181 0.0324 -3.6408 0.0004
season4 -0.3467 0.0324 -10.6900 0.0000
season5 -0.5050 0.0324 -15.5680 0.0000
season6 -0.4243 0.0324 -13.0771 0.0000
season7 -0.2037 0.0325 -6.2784 0.0000
season8 -0.3326 0.0325 -10.2482 0.0000
season9 -0.6091 0.0325 -18.7601 0.0000
season10 -0.5293 0.0325 -16.2990 0.0000
season11 -0.3263 0.0325 -10.0431 0.0000
season12 -0.1042 0.0325 -3.2068 0.0018- Pronóstico de \(W_t = log (Y_t)\).
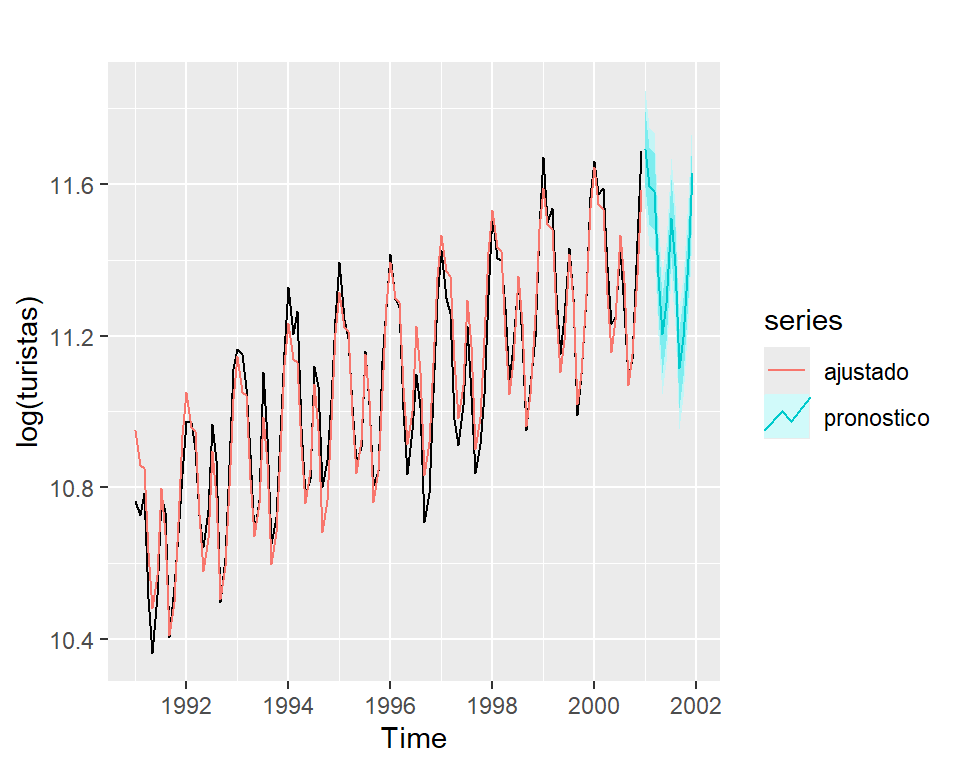
- La ventaja de
tslmes que se puede especificar la transformación con el argumenlambda.
Call:
tslm(formula = y ~ trend + I(trend^2) + season, lambda = 0)
Residuals:
Min 1Q Median 3Q Max
-0.188378 -0.048245 0.007514 0.052592 0.135323
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 1.094e+01 2.940e-02 372.182 < 2e-16 ***
trend 8.617e-03 7.707e-04 11.181 < 2e-16 ***
I(trend^2) -1.992e-05 6.169e-06 -3.229 0.001654 **
season2 -1.013e-01 3.243e-02 -3.125 0.002297 **
season3 -1.181e-01 3.243e-02 -3.641 0.000422 ***
season4 -3.467e-01 3.243e-02 -10.690 < 2e-16 ***
season5 -5.050e-01 3.244e-02 -15.568 < 2e-16 ***
season6 -4.243e-01 3.244e-02 -13.077 < 2e-16 ***
season7 -2.037e-01 3.245e-02 -6.278 7.65e-09 ***
season8 -3.326e-01 3.246e-02 -10.248 < 2e-16 ***
season9 -6.091e-01 3.247e-02 -18.760 < 2e-16 ***
season10 -5.293e-01 3.248e-02 -16.299 < 2e-16 ***
season11 -3.263e-01 3.249e-02 -10.043 < 2e-16 ***
season12 -1.042e-01 3.250e-02 -3.207 0.001775 **
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 0.07251 on 106 degrees of freedom
Multiple R-squared: 0.9439, Adjusted R-squared: 0.937
F-statistic: 137.3 on 13 and 106 DF, p-value: < 2.2e-16Pronósticos usando regresión
Contenido
Introducción
Modelos de regresión
Regresión espuria
El tiempo como covariables
Pronósticos usando regresión
Extensiones de modelos de regresión
Pronósticos usando regresión
y<-ts(turistas$turistas,start=c(1991,1),frequency=12)
y.train<-window(y,start=c(1991,1),end=c(1999,12))
y.test<-window(y,start=c(2000,1),end=c(2000,12))
mod4<-tslm(y.train~trend+I(trend^2)+season, lambda = 0)
summary(mod4)
Call:
tslm(formula = y.train ~ trend + I(trend^2) + season, lambda = 0)
Residuals:
Min 1Q Median 3Q Max
-0.17475 -0.04751 0.00836 0.04812 0.13057
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 1.093e+01 3.104e-02 352.036 < 2e-16 ***
trend 9.663e-03 9.059e-04 10.667 < 2e-16 ***
I(trend^2) -3.135e-05 8.048e-06 -3.895 0.000184 ***
season2 -1.023e-01 3.427e-02 -2.986 0.003605 **
season3 -1.221e-01 3.427e-02 -3.561 0.000581 ***
season4 -3.528e-01 3.428e-02 -10.291 < 2e-16 ***
season5 -5.110e-01 3.428e-02 -14.905 < 2e-16 ***
season6 -4.229e-01 3.429e-02 -12.335 < 2e-16 ***
season7 -1.969e-01 3.430e-02 -5.741 1.15e-07 ***
season8 -3.217e-01 3.431e-02 -9.376 3.89e-15 ***
season9 -6.078e-01 3.432e-02 -17.713 < 2e-16 ***
season10 -5.245e-01 3.433e-02 -15.277 < 2e-16 ***
season11 -3.327e-01 3.434e-02 -9.688 8.44e-16 ***
season12 -1.116e-01 3.436e-02 -3.249 0.001606 **
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 0.0727 on 94 degrees of freedom
Multiple R-squared: 0.9382, Adjusted R-squared: 0.9296
F-statistic: 109.7 on 13 and 94 DF, p-value: < 2.2e-16 Point Forecast Lo 80 Hi 80 Lo 95 Hi 95
Jan 2000 109989.74 99272.84 121863.56 93941.82 128779.09
Feb 2000 99569.71 89844.97 110347.04 85008.45 116625.19
Mar 2000 97891.63 88306.78 108516.81 83540.84 114707.61
Apr 2000 77932.30 70281.62 86415.81 66478.26 91359.84
May 2000 66701.49 60135.29 73984.66 56871.81 78230.13
Jun 2000 73026.02 65816.53 81025.24 62234.20 85689.22
Jul 2000 91775.62 82687.92 101862.10 78173.48 107744.53
Aug 2000 81205.70 73139.61 90161.35 69133.73 95385.65
Sep 2000 61139.77 55047.22 67906.64 52022.30 71855.18
Oct 2000 66609.59 59949.83 74009.18 56644.23 78328.14
Nov 2000 80866.86 72753.77 89884.68 68728.01 95149.70
Dec 2000 101095.83 90917.22 112413.98 85868.09 119024.03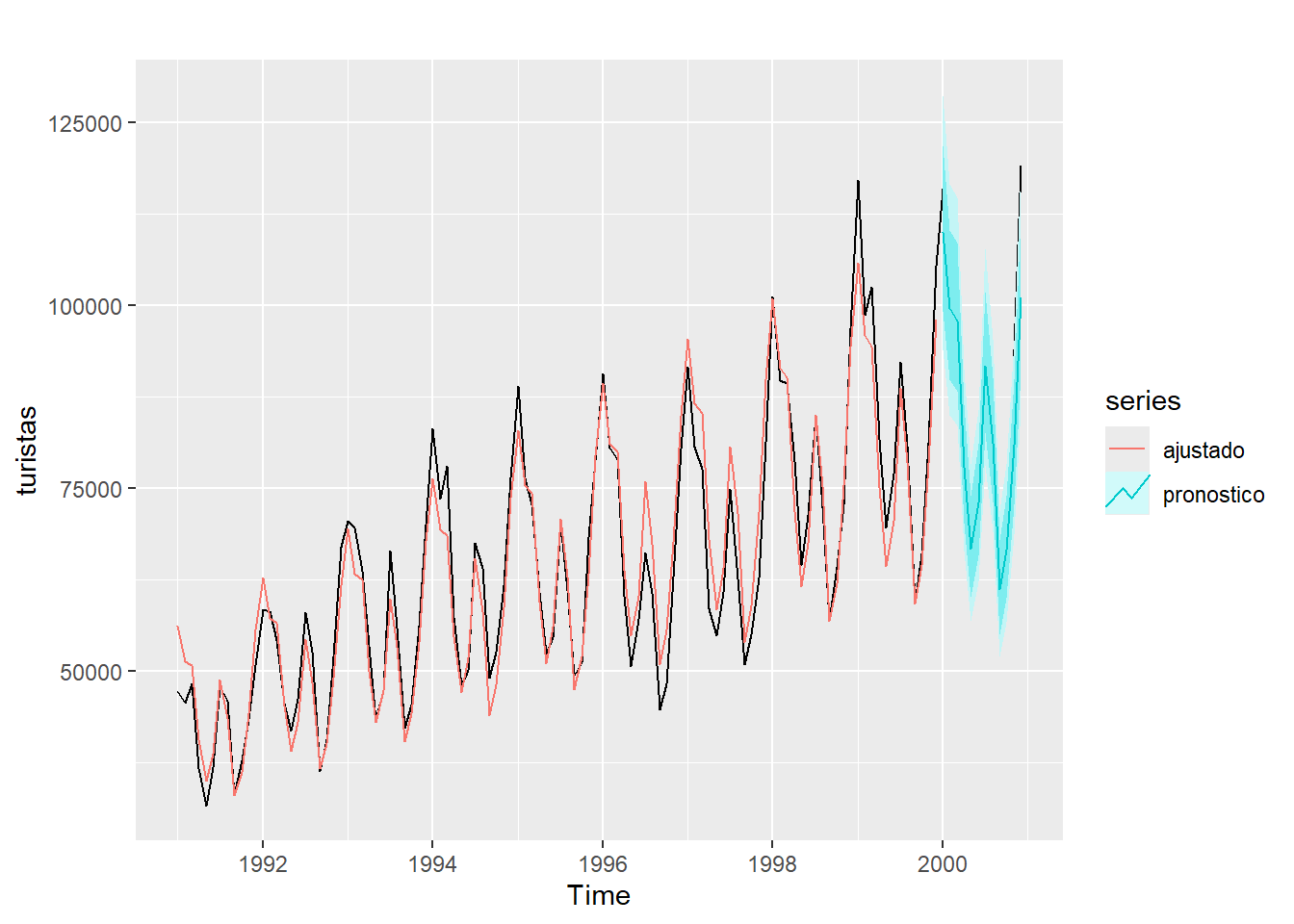
Extensiones de modelos de regresión
Contenido
Introducción
Modelos de regresión
Regresión espuria
El tiempo como covariables
Pronósticos usando regresión
Extensiones de modelos de regresión
Extensiones de modelos de regresión
Modelos no lineales.
Modelos lineales generalizados (GLM).
- Variables dependientes que pertenecen a una familia exponencial: Poisson, Exponencial, etc.
Modelos aditivos generalizados (GAM).
- Efectos fijos y aleatorios.
Modelos aditivos generalizados para locación, escala y forma (GAMLSS).
Ejemplo
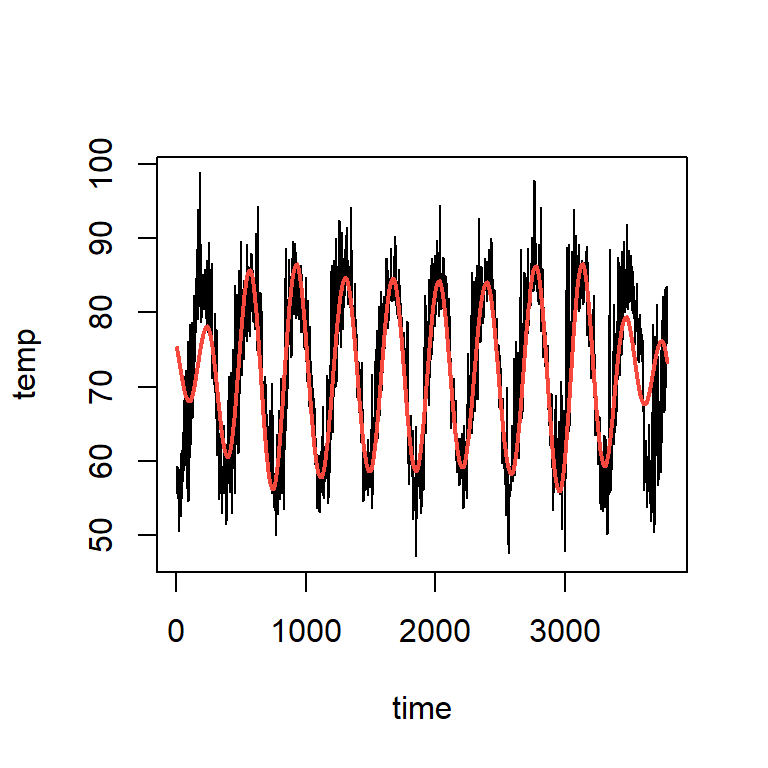
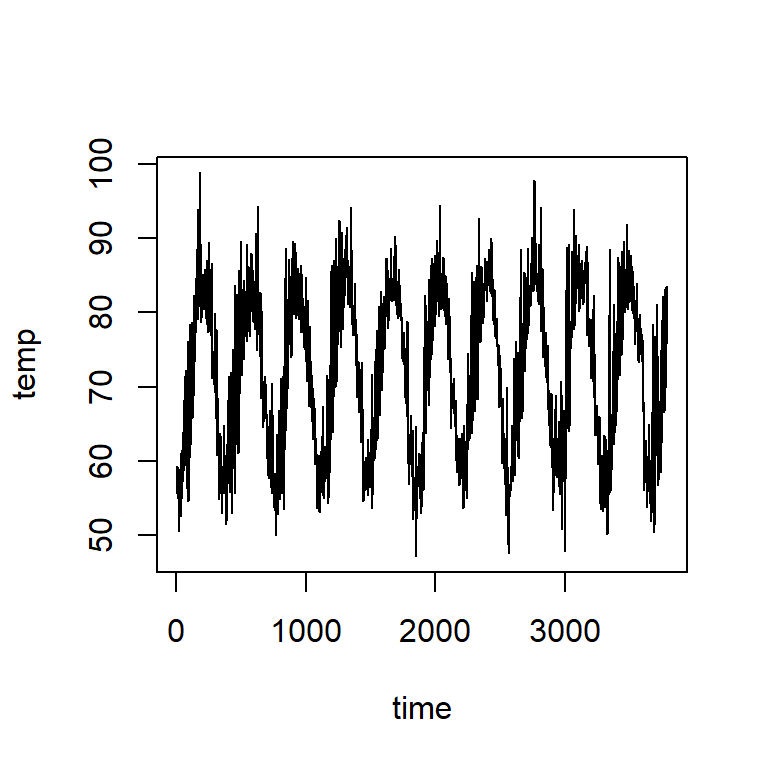
Temperatura diaria (F) en Cairo de 01-01-1995 hasta 21-05-2005
- Ajuste de un GAM
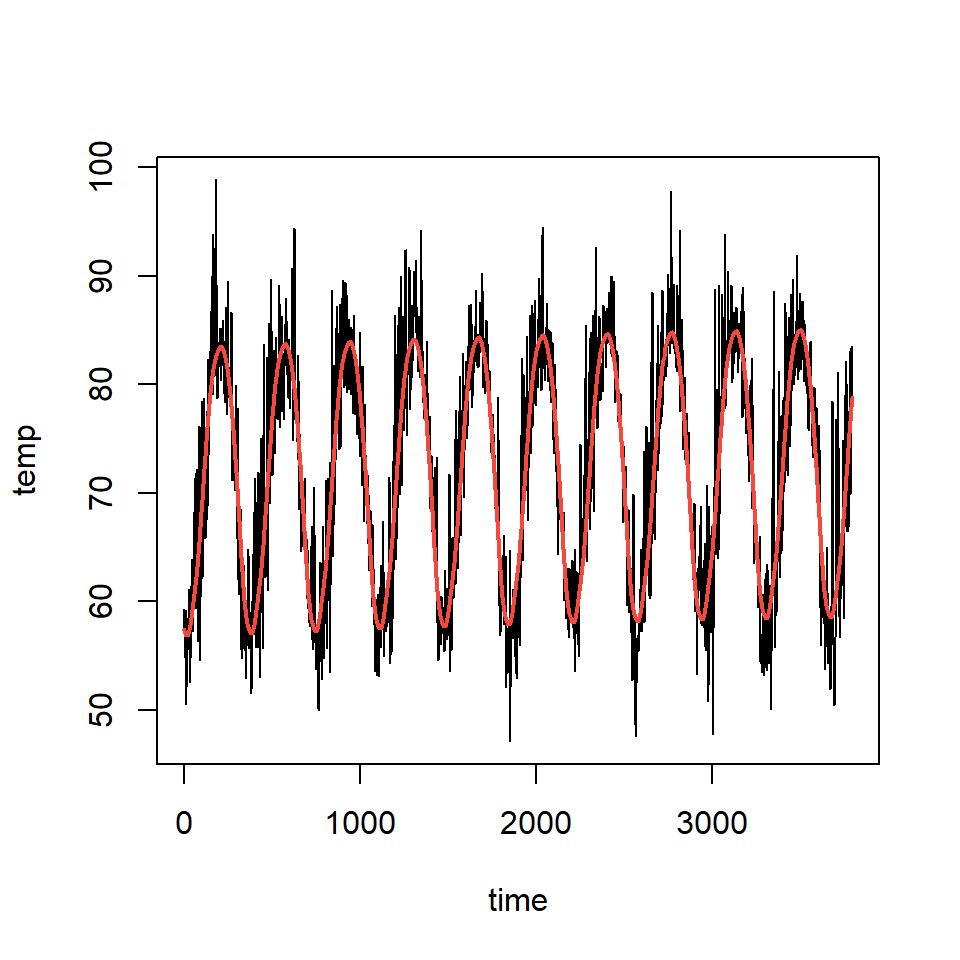
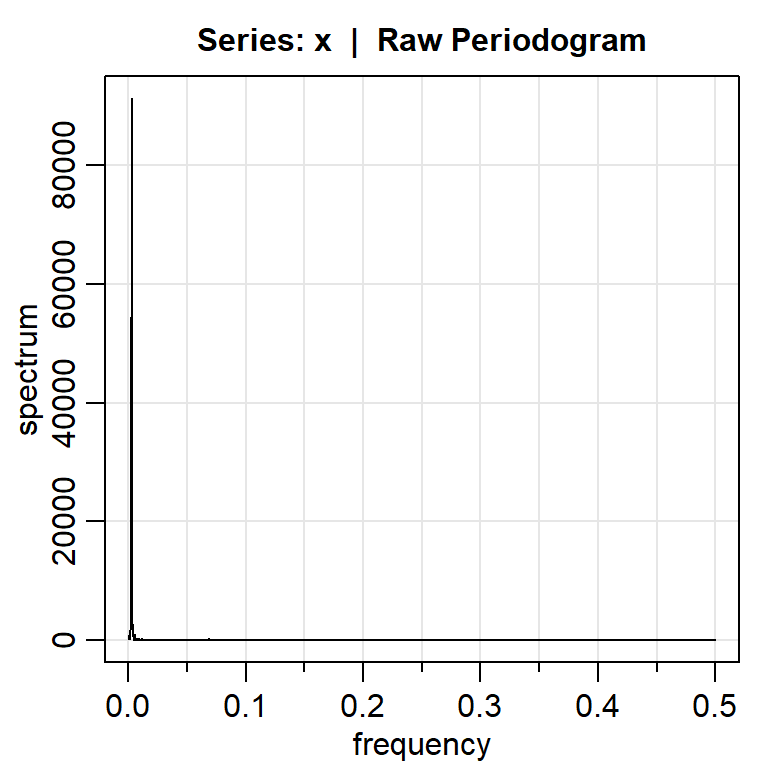
La frecuencia dominante \(\omega\) es 0.002864583, es decir, se completa un ciclo aproximadamente cada 349.09 días.
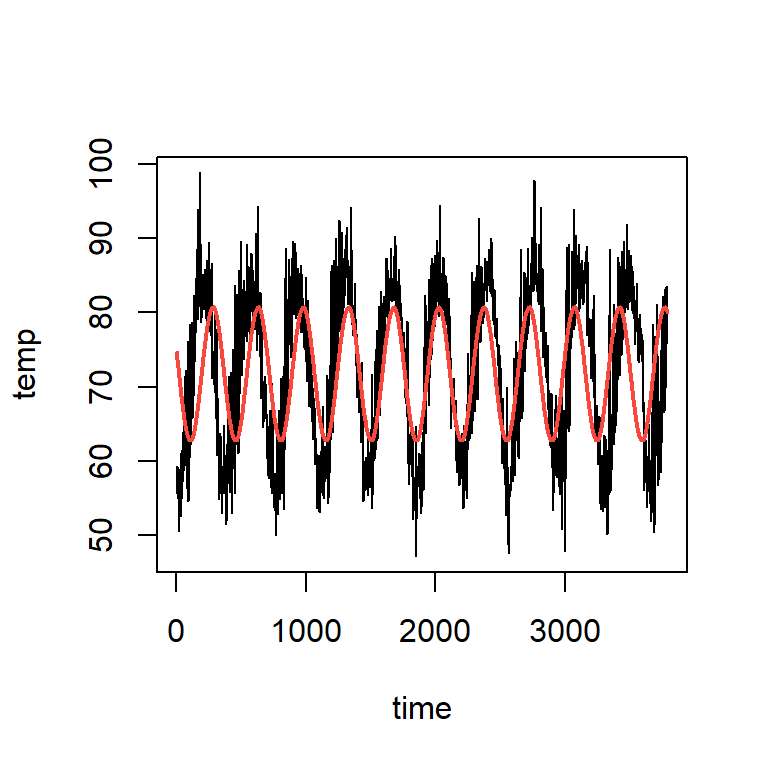
- Modelo de regresión lineal con covariables senos y cosenos \[y_t=\alpha+\beta_1 cos(2 \pi \omega t)+\beta_2 sen(2 \pi \omega t)+\varepsilon_t\]
- Modelo de regresión lineal con covariables senos y cosenos con 5 frecuencias más importantes:
\[y_t=\alpha+ \sum_{k=1}^{5} \left[ \beta_{1k} cos(2 \pi \omega_k t)+\beta_{2k} sen(2 \pi \omega_k t) \right]+\varepsilon_t\]
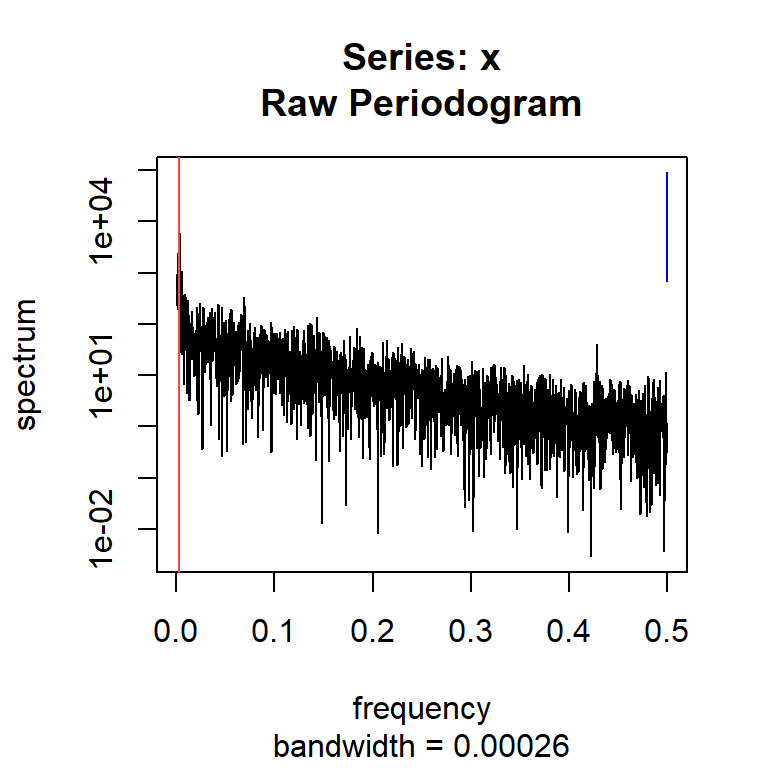
- Las 8 frecuencias más importantes:
frequency period spectrum
1 0.0029 349.0909 91251.731
2 0.0026 384.0000 54420.640
3 0.0023 426.6667 8986.496
4 0.0031 320.0000 6148.723
5 0.0034 295.3846 2902.172
6 0.0021 480.0000 2409.255
7 0.0018 548.5714 1666.177
8 0.0039 256.0000 1331.423frecuencia1 <- spectro_orden$frequency[1]
frecuencia2 <- spectro_orden$frequency[2]
frecuencia3 <- spectro_orden$frequency[3]
frecuencia4 <- spectro_orden$frequency[4]
frecuencia5 <- spectro_orden$frequency[5]
cos1<-cos(2*pi*frecuencia1*cairo$time)
sin1<-sin(2*pi*frecuencia1*cairo$time)
cos2<-cos(2*pi*frecuencia2*cairo$time)
sin2<-sin(2*pi*frecuencia2*cairo$time)
cos3<-cos(2*pi*frecuencia3*cairo$time)
sin3<-sin(2*pi*frecuencia3*cairo$time)
cos4<-cos(2*pi*frecuencia4*cairo$time)
sin4<-sin(2*pi*frecuencia4*cairo$time)
cos5<-cos(2*pi*frecuencia5*cairo$time)
sin5<-sin(2*pi*frecuencia5*cairo$time)
data=data.frame(x=x,
cos1=cos1,sen1=sin1,
cos2=cos2,sen2=sin2,
cos3=cos3,sen3=sin3,
cos4=cos4,sen4=sin4,
cos5=cos5,sen5=sin5)
mod2<-lm(x~.,data=data)
plot(cairo$temp~cairo$time,type="l", ylab="temp",xlab="time")
points(cairo$time,fitted(mod2),type="l",col=2,lwd=2)