Tema 6: Modelos ARIMA de Box&Jenkins⁽¹⁾

shuwei.chou@ucr.ac.cr

Escuela de Estadística, Universidad de Costa Rica

Paquetes de R

Para este tema, se necesita cargar estos paquetes:

library(ggplot2)
library(forecast)
library(fpp2)
library(astsa)

Modelos ARIMA

Contenido

Modelos ARIMA
AR(1) y AR(2)
MA(1) y MA(2)
ARMA(1,1)

Modelos ARIMA

ARIMA se refiere a AutoRegressive Integrated Moving Average.
Es un conjunto de modelos en que cada modelo tiene una función de autocorrelación teórica y una función de autocorrelación parcial teórica específica.
La idea del enfoque de Box-Jenkins es que compara estas funciones teóricas con las respectivas funciones muestrales de autocorrelación y de autocorrelación parcial con el fin de identificar y ajustar el modelo apropiado.

AR(1) y AR(2)

Contenido

Modelos ARIMA
AR(1) y AR(2)
MA(1) y MA(2)
ARMA(1,1)

AR(1)

El AR(1), modelo no estacional autorregresivo de orden 1, está definido por el siguiente proceso estocástico lineal:

\[Z_t=C+\phi_1 Z_{t-1}+a_t\] donde:
\(C\) y \(\phi_1\) son constantes desconocidas,
\(a_t \sim wn(0,\sigma_a^2)\) (independiente de \(Z_t\)), i.e. una sucesión de v.a. mutuamente no correlacionadas e idénticamente distribuidas con media \(0\) y variancia \(\sigma_a^2\).

Nota

Generalmente se supone que \(a_t\) es ruido blanco gaussiano.

Recursivamente se puede obtener:

\[\begin{align*} Z_t &= C + \phi_1 Z_{t-1} + a_t \\ &= C + \phi_1(C + \phi_1 Z_{t-2} + a_{t-1}) + a_t \\ &= C(1 + \phi_1 + \phi_1^2 + \cdots + \phi_1^{J-1}) + a_t + \phi_1 a_{t-1} + \phi_1^2 a_{t-2} + \cdots + \phi_1^{J-1} a_{t-(J-1)} + \phi_1^J Z_{t-J} \\ &= C \left( \frac{1 - \phi_1^J}{1 - \phi_1} \right) + \sum_{j=0}^{J-1} \phi_1^j a_{t-j} + \phi_1^J Z_{t-J} \end{align*}\]

Recursivamente se puede obtener una serie infinita: \[Z_t=C \left( \frac{1-\phi_1^J}{1-\phi_1} \right)+\sum_{j=0}^{J-1} \phi_1^j a_{t-j}+\phi_1^J Z_{t-J}\] En el caso de \(|\phi_1|<1\), cuando \(J \rightarrow \infty\),

\[Z_t=C \left( \frac{1}{1-\phi_1} \right)+\sum_{j=0}^{\infty} \phi_1^j a_{t-j}\]

Como \(\mathbb{E}(a_t)=0\) para todo \(t\), \[E(Z_t)=C \left( \frac{1}{1-\phi_1}\right)=\mu, ~~\text{es independiente de}~ t.\]
Además, \(\mathrm{Var}(a_t)=\sigma_a^2\) para todo \(t\), \[\mathrm{Var}(Z_t)=\sum_{j=0}^{\infty} \phi_1^{2j} \mathrm{Var}(a_{t-j})=\left( \frac{1}{1-\phi_1^2} \right) \sigma_a^2\] es finito e independiente de \(t\).

Puesto que \(Z_t-\mu=\sum\limits_{j=0}^{\infty} \phi_1^j a_{t-j}\), la función de autocovariancia es

\[\begin{aligned} \gamma_Z(t, t-k) &= \mathrm{Cov}(Z_t, Z_{t-k}) = \mathbb{E}\left[(Z_t - \mu)(Z_{t-k} - \mu)\right] \\ &= \mathbb{E} \left[ \left( \sum_{i=0}^{\infty} \phi_1^i a_{t-i} \right) \left( \sum_{j=0}^{\infty} \phi_1^j a_{t-k-j} \right) \right] \end{aligned}\]

Tome \(m=k+j (o~ j=m-k)\),

\[\begin{aligned} \gamma_Z(t, t-k) &= \mathbb{E}\left[ \left(\sum_{i=0}^{\infty} \phi_1^i a_{t-i}\right) \left( \sum_{m=k}^{\infty} \phi_1^{m-k} a_{t-m} \right) \right] \\ &= \mathbb{E}\left[ \left( \sum_{i=0}^{k-1} \phi_1^i a_{t-i} + \sum_{i=k}^{\infty} \phi_1^i a_{t-i} \right) \left( \sum_{m=k}^{\infty} \phi_1^{m-k} a_{t-m} \right) \right]. \end{aligned}\]

\[\begin{aligned} \gamma_Z(t, t-k) &= \mathbb{E}\left[ \left( \sum_{i=0}^{k-1} \phi_1^i a_{t-i} + \sum_{i=k}^{\infty} \phi_1^i a_{t-i} \right) \left( \sum_{m=k}^{\infty} \phi_1^{m-k} a_{t-m} \right) \right] \\ &= \mathbb{E}\left[ \left( \sum_{i=k}^{\infty} \phi_1^i a_{t-i} \right) \left( \sum_{m=k}^{\infty} \phi_1^{m-k} a_{t-m} \right) \right] = \sum_{i=k}^{\infty} \phi_1^i \phi_1^{i-k} \mathbb{E}[a_{t-i}^2] \\ &= \sigma_a^2 \sum_{j=0}^{\infty} \phi_1^{k+j} \phi_1^j \quad \text{(tomando } j = i - k\text{)} \\ &= \phi_1^k \sigma_a^2 \sum_{j=0}^{\infty} \phi_1^{2j} = \phi_1^k \sigma_a^2 \cdot \frac{1}{1 - \phi_1^2} \\ &= \phi_1^k \, \mathrm{Var}(Z_t), \quad \text{para } k = 1, 2, \ldots \end{aligned}\]

depende únicamente del regazo \(k\), y es independiente de \(t\).

Por lo tanto, el proceso AR(1) es estacionario si \(|\phi_1|<1\).

La función de autocorrelación teórica es:

\[\begin{aligned} \rho_k &= \frac{\mathrm{Cov}(Z_t, Z_{t-k})}{\sqrt{\mathrm{Var}(Z_t)\mathrm{Var}(Z_{t-k})}} = \frac{\mathrm{Cov}(Z_t, Z_{t-k})}{\mathrm{Var}(Z_t)} \\ &= \frac{\phi_1^k \, \mathrm{Var}(Z_t)}{\mathrm{Var}(Z_t)} = \phi_1^k, \quad k = 1, 2, \ldots \end{aligned}\]

Note que la función de autocorrelación teórica decae exponencialmente a cero.

La función de autocorrelación teórica de un AR(1) es:

\[\rho_k=\phi_1^k,~k=1,2,...\]

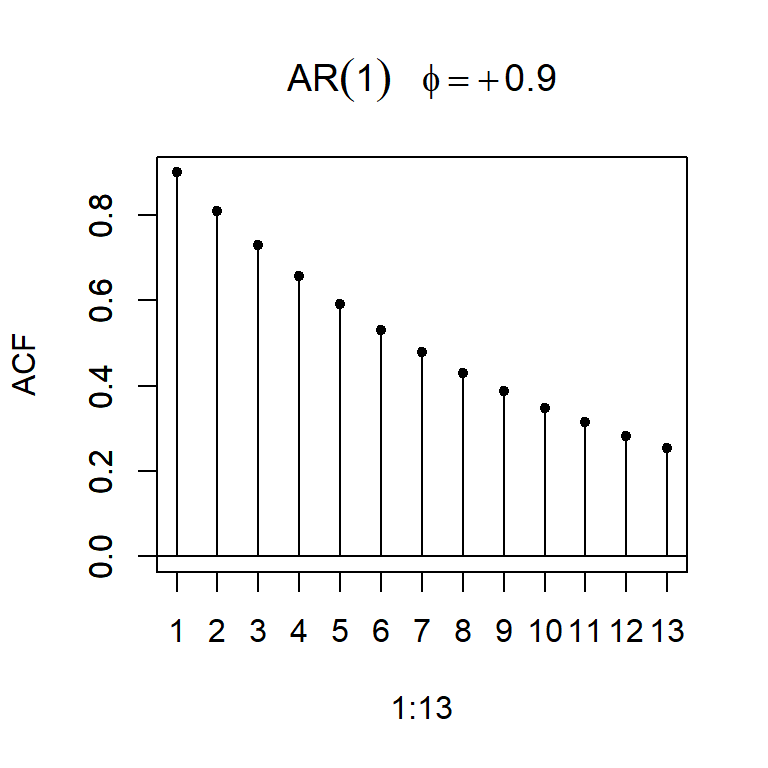
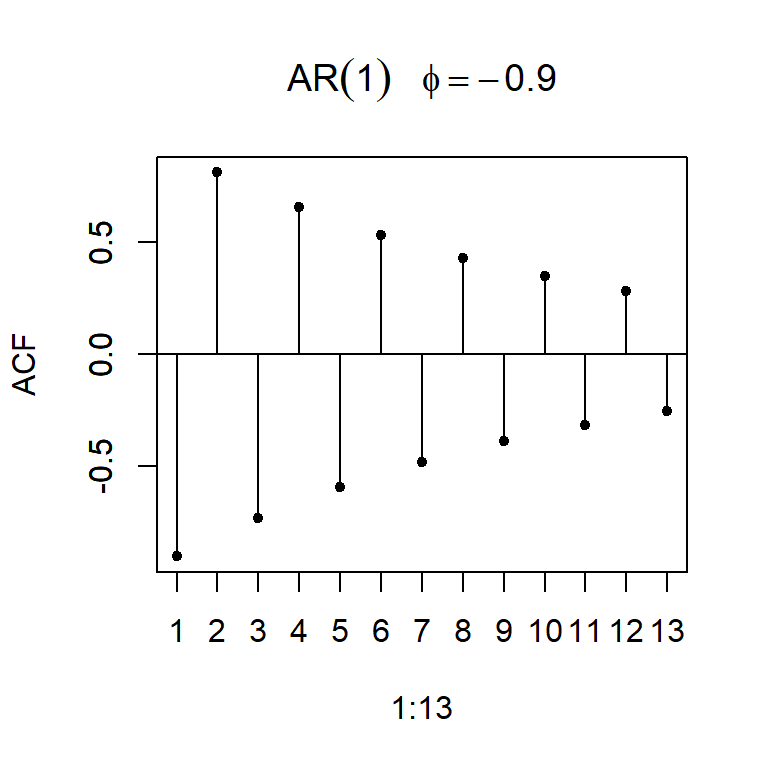
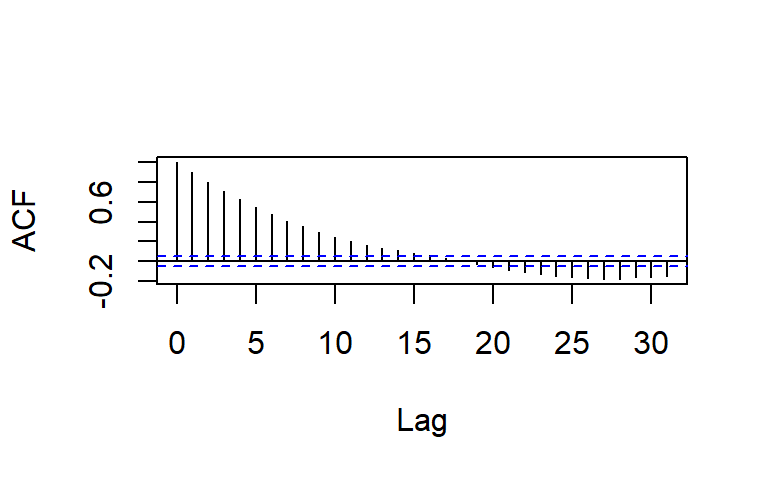
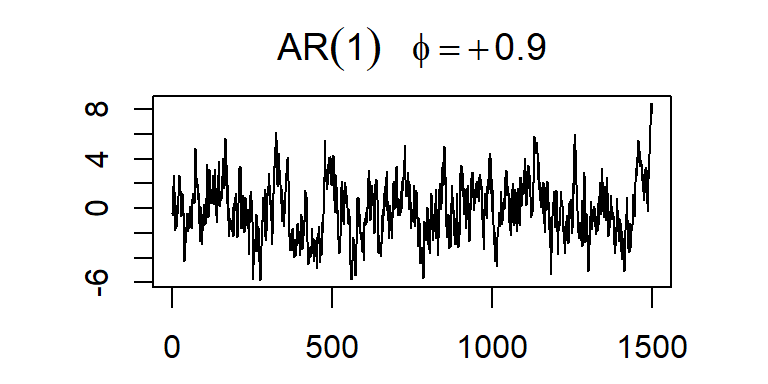
Considere \(a_t \sim N(0,1)\), y un modelo AR(1): \[Z_t=\phi_1 Z_{t-1}+a_t\]

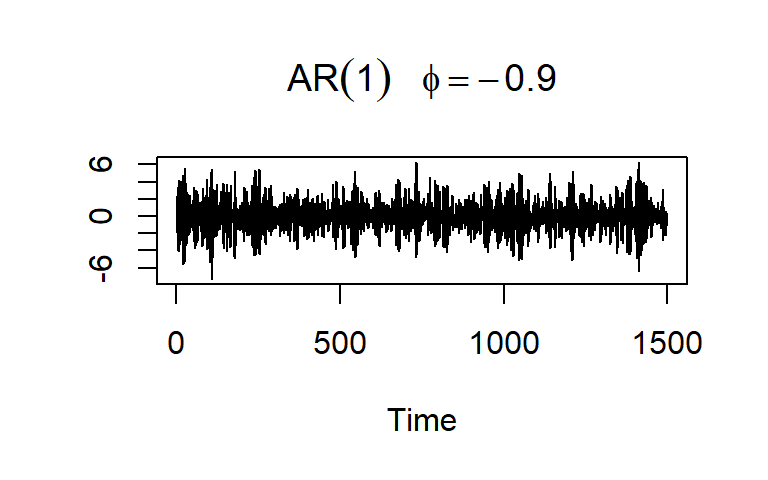
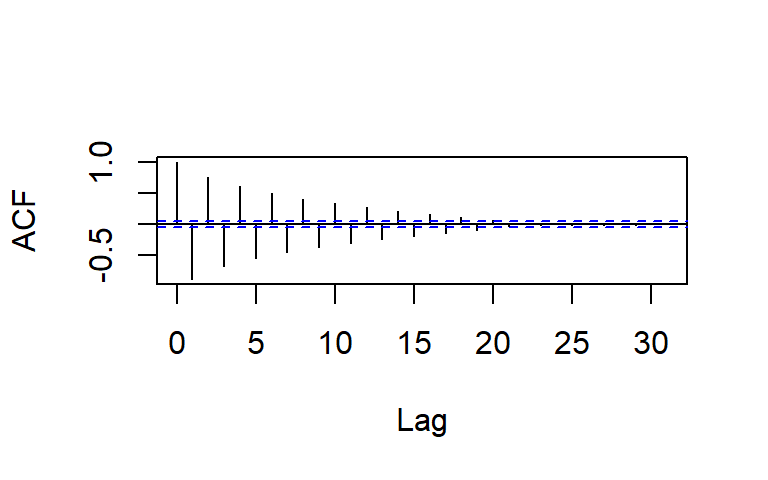
AR(2)

El AR(2), modelo no estacional autorregresivo de orden 2, está definido por el siguiente proceso estocástico lineal:

\[Z_t=C+\phi_1 Z_{t-1}+\phi_2 Z_{t-2}+a_t\] donde:
\(C\), \(\phi_1\) y \(\phi_2\) son constantes desconocidas,
\(a_t \sim wn(0,\sigma_a^2)\) (independiente de \(Y_t\)).

Se puede mostrar que el proceso AR(2) es estacionario si:
- \(|\phi_2|<1\).
- \(\phi_1+\phi_2<1\).
- \(-\phi_1+\phi_2<1\).

Se puede mostrar que:

\(\mathbb{E}(Z_t)= \frac{C}{1-\phi_1-\phi_2}=\mu\) es independiente de \(t\).
\(\mathrm{Var}(Z_t)=\frac{(1-\phi_2) \sigma_a^2}{(1+\phi_2)(1-\phi_1-\phi_2)(1+\phi_1-\phi_2)}\) es independiente de \(t\) y finito.
La función de autocorrelación teórica, \(\rho_k\), es dada por:

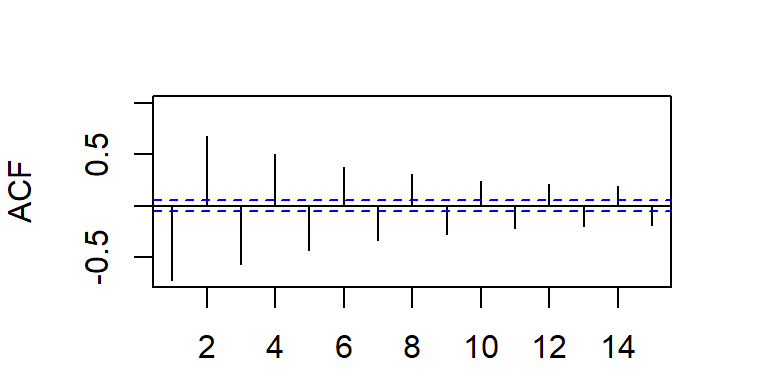
\[\begin{aligned} \rho_1 &= \frac{\phi_1}{1 - \phi_2} \\[1ex] \rho_2 &= \frac{\phi_1^2}{1 - \phi_2} + \phi_2 \\[1ex] \rho_k &= \phi_1 \rho_{k-1} + \phi_2 \rho_{k-2}, \quad \text{para } k \geq 3 \end{aligned}\]

Bajo las condiciones de estacionariedad, \(\rho_k\) depende únicamente de \(k\) y no depende del \(t\) y decae hacia cero según una combinación de exponenciales y/o ondas sinusoidales amortiguadas.

La función de autocorrelación teórica de un AR(2):

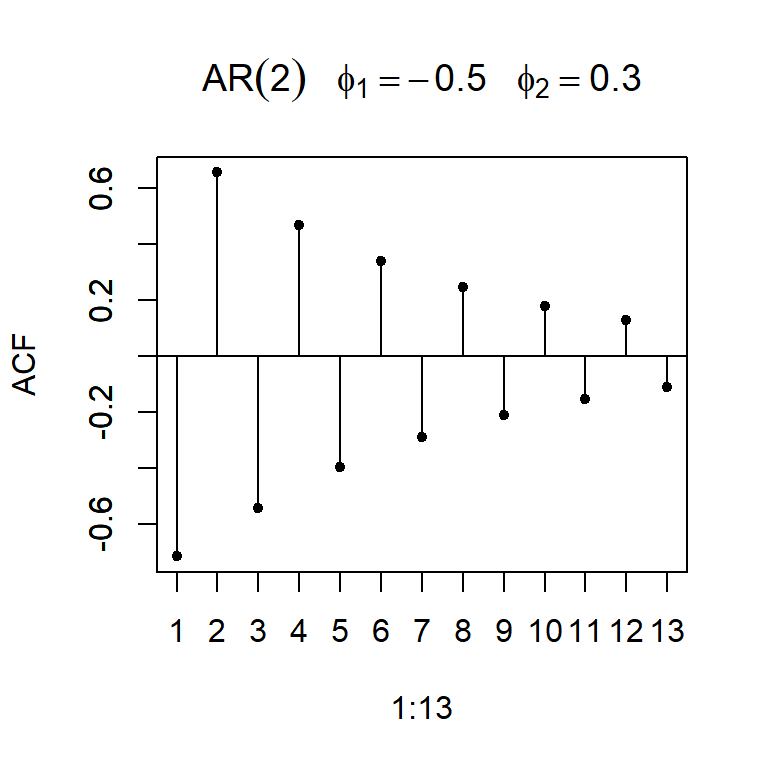
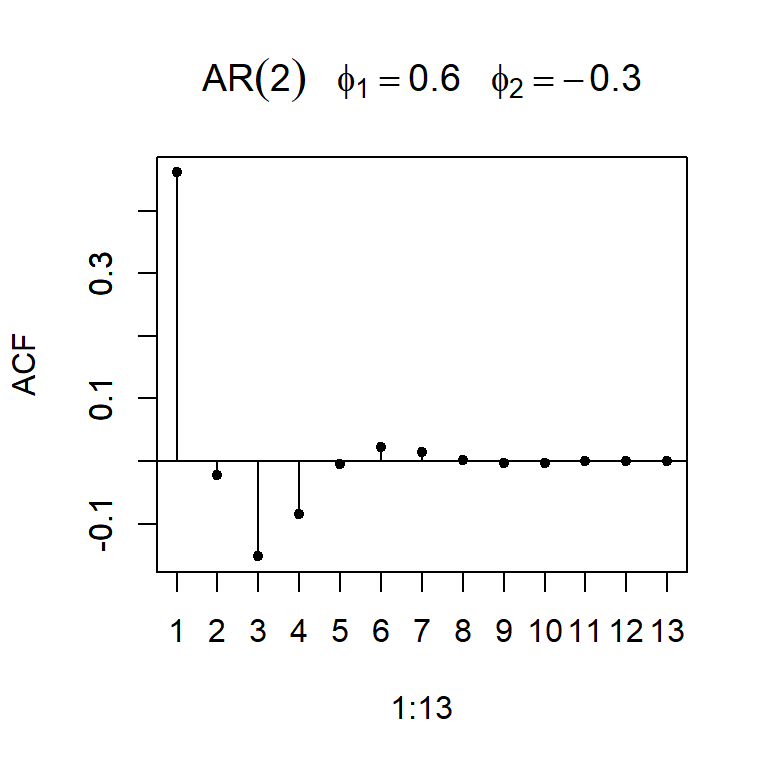
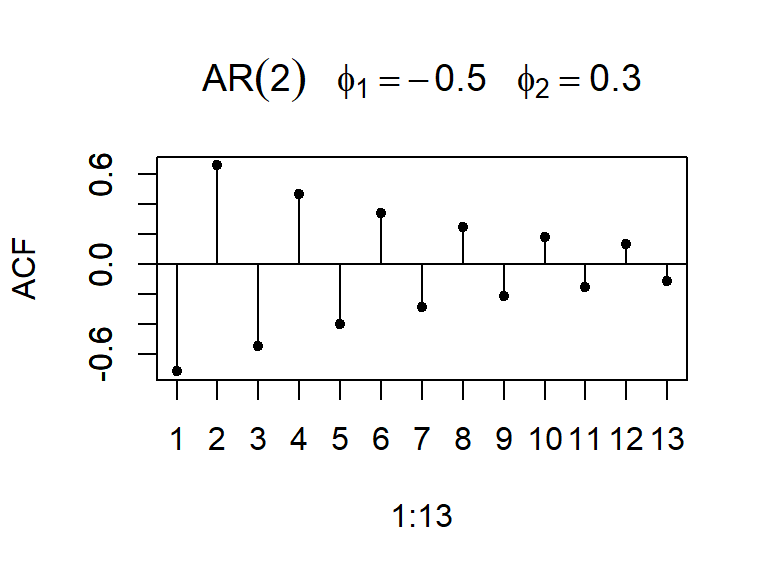
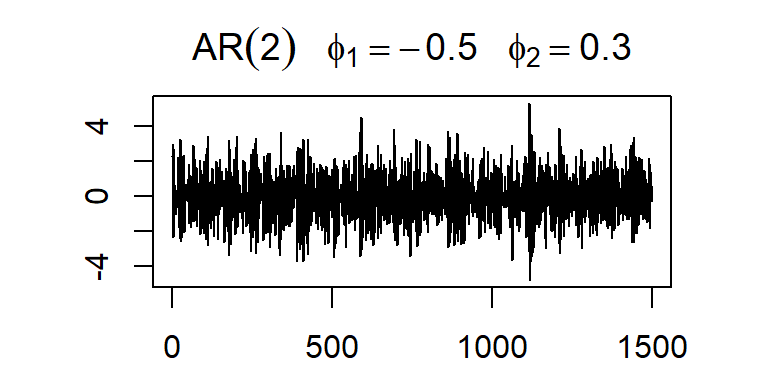
Considere \(a_t \sim N(0,1)\), y un modelo AR(2): \[Z_t=\phi_1 Z_{t-1}+\phi_2 Z_{t-2}+a_t\]

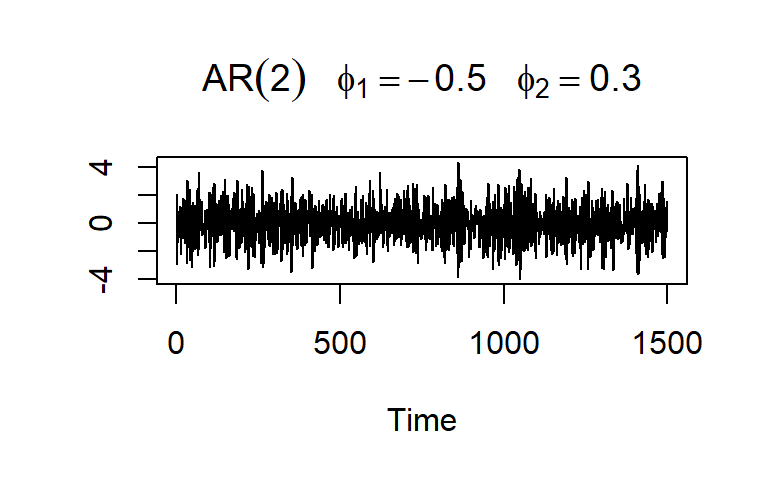
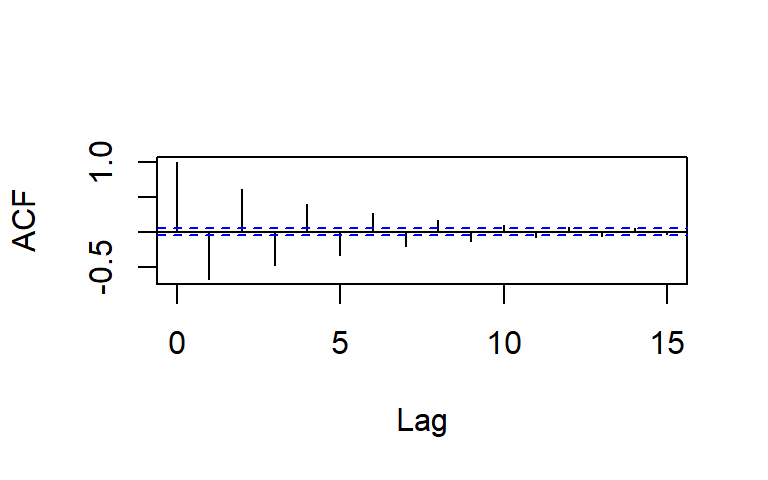
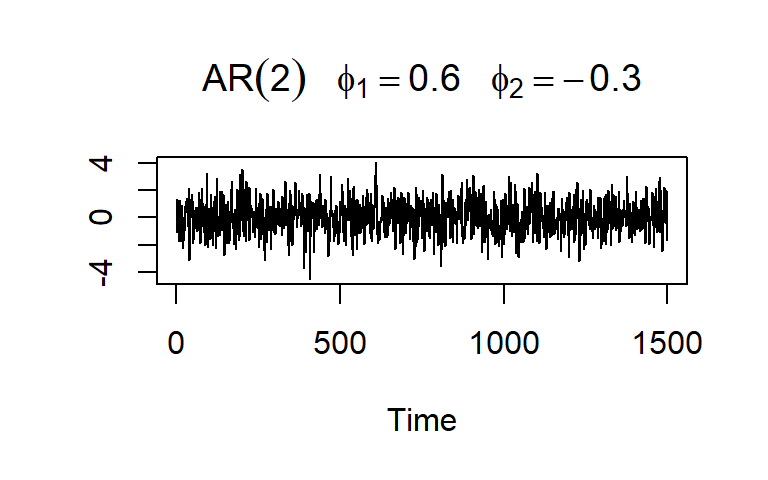
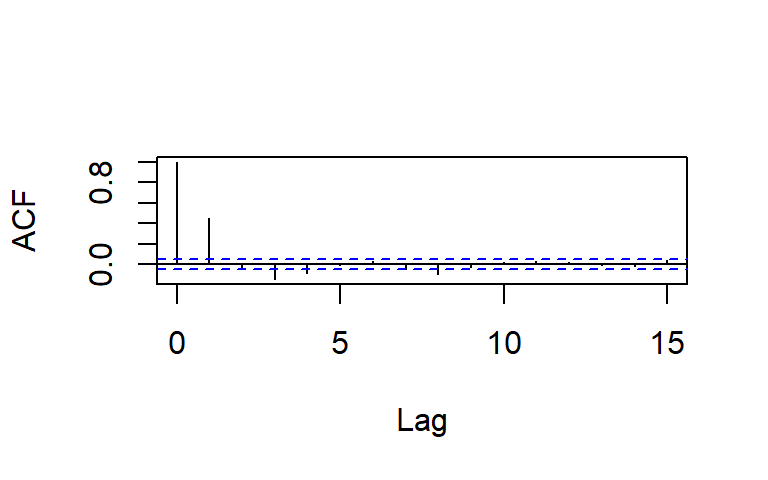
La función de autocorrelación parcial

La autocorrelación parcial (PACF) en el rezago \(k\) mide el grado de asociación lineal entre \(Z_t\) y \(Z_{t-k}\) cuando los efectos de los otros rezagos \(1,2,...,k-1\) han sido eliminados.
Denotemos la función de autocorrelación parcial teórica de orden \(k\) por \(\rho_{kk}\) para \(k=1,2,...\) y la función de autocorrelación parcial muestral de orden \(k\) con \(r_{kk}\), para \(k=1,2,...\).
Teóricamente la función de autocorrelación parcial de un proceso estacionario \(Z_t\), denotado por \(\rho_{kk}\), para \(k=1,2,...\) es \[\rho_{11}=corr(Z_{t+1},Z_t)=\rho_1, ~~~~\text{y}\]

\[\rho_{kk}=corr\left[Z_{t+k}-\hat{Z}_{t+k}~,~Z_t-\hat{Z}_{t}\right],~~\text{para}~~ k \geq 2,\] donde
\(\hat{Z}_{t+k}=\beta_1 Z_{t+k-1}+\beta_2 Z_{t+k-2}+...+\beta_{h-1} Z_{t+1}\)
\(\hat{Z}_{t}=\beta_1 Z_{t+1}+\beta_2 Z_{t+2}+...+\beta_{h-1} Z_{t+k-1}\)

Si \(Z_t\) es un proceso gaussiano, \[\rho_{kk}=corr(Z_{t+k},Z_t|Z_{t+1},...,Z_{t+k-1}).\] i.e. es la correlación de una distribución normal bivariada \((Z_{t+k},Z_t)\) condicional a \({Z_{t+1},...,Z_{t+k-1}}\).
Se puede comprobar que:

Para AR(1):

\(\rho_{11}=\phi_1\)
\(\rho_{kk}=0\) para \(k \geq 2\).
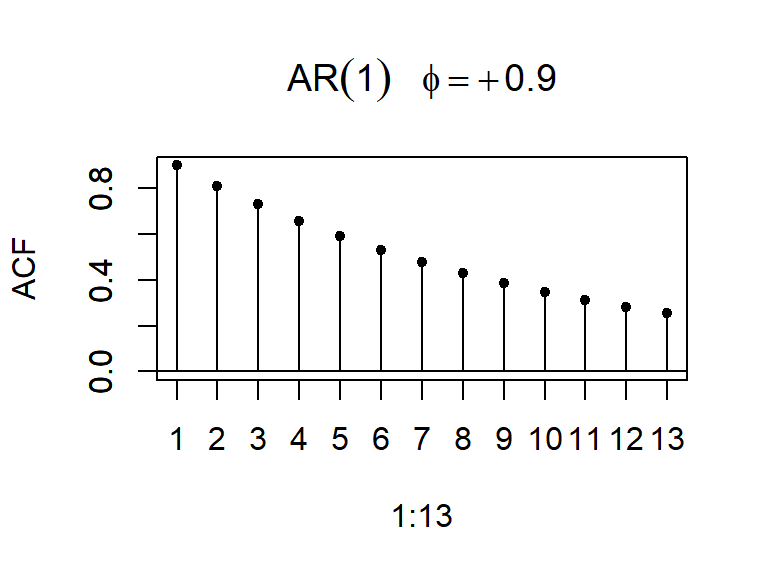
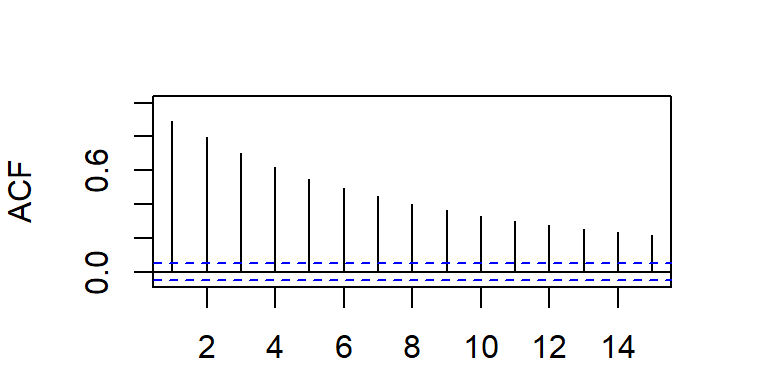
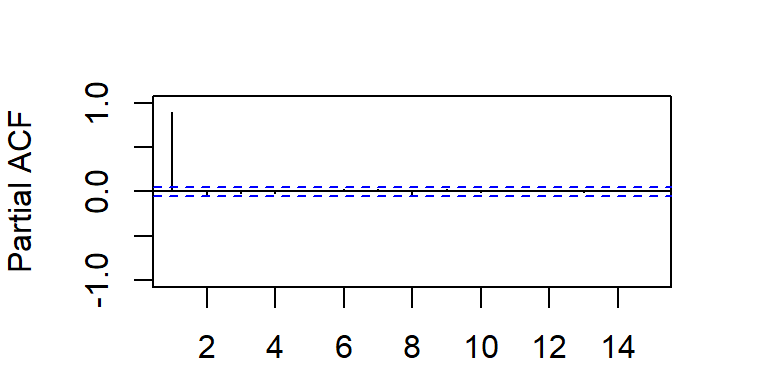
La función de autocorrelación parcial cae bruscamente a cero después del rezago 1.

Para AR(2):

\(\rho_{11}=\rho_1=\frac{\phi_1}{1-\phi_2}\)
\(\rho_{22}=\phi_2\)
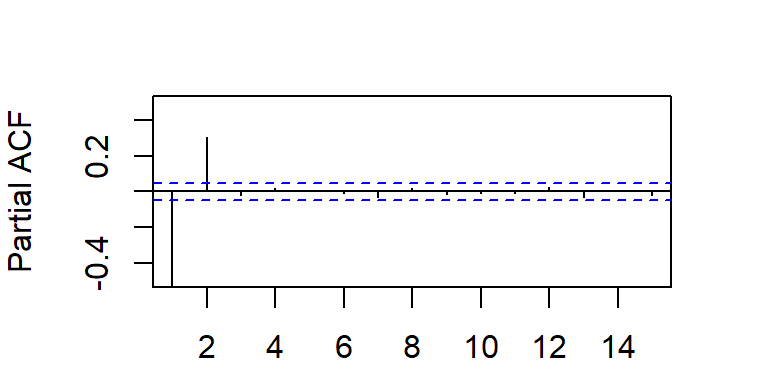
\(\rho_{kk}=0\) para \(k \geq 3\).
La función de autocorrelación parcial cae bruscamente a cero después del rezago 2.

ACF y PACF teórica y empírica de un AR(1)

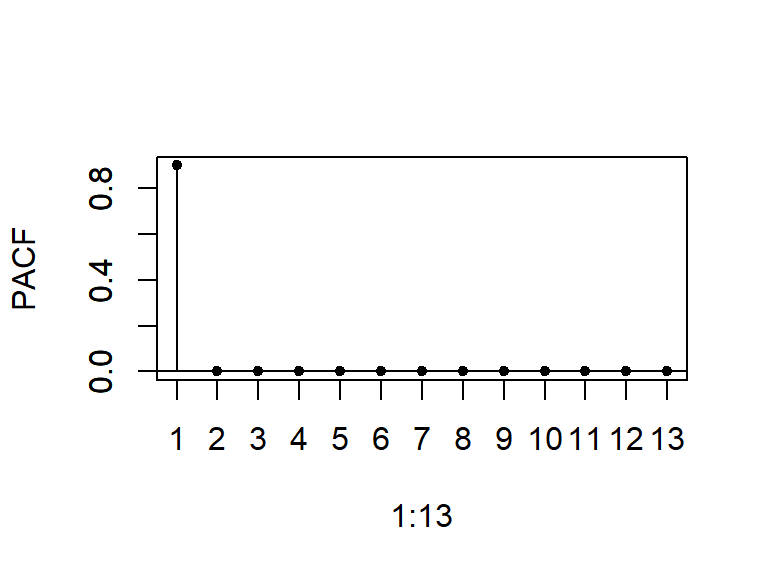
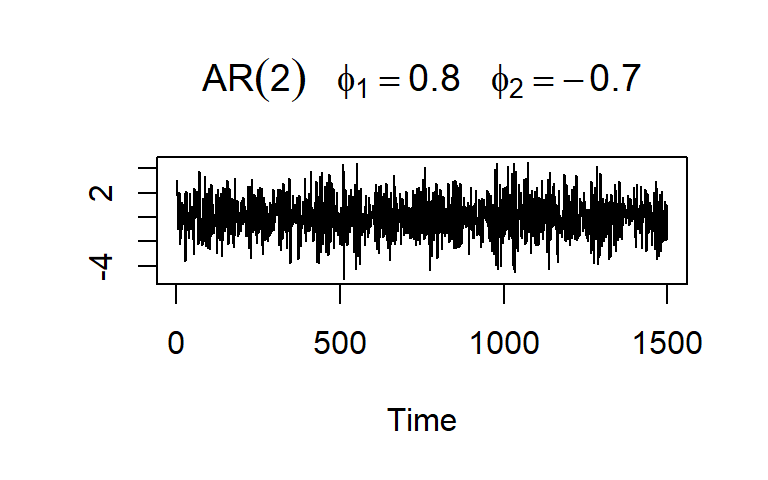
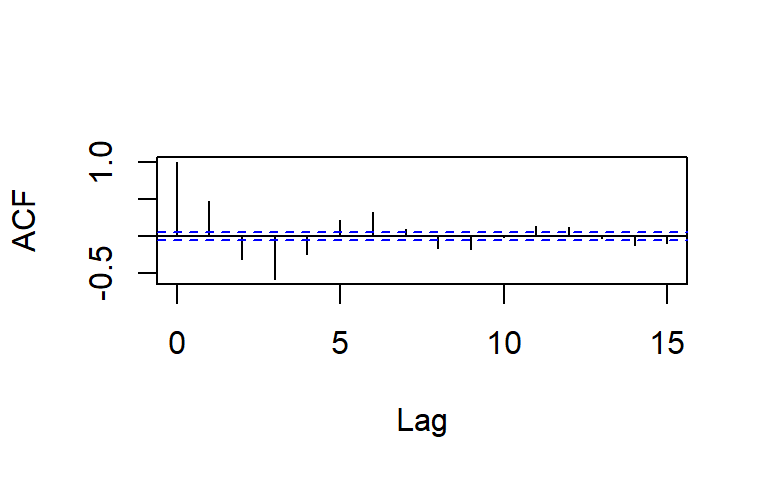
La ACF y PACF teórica y empírica de un AR(2)

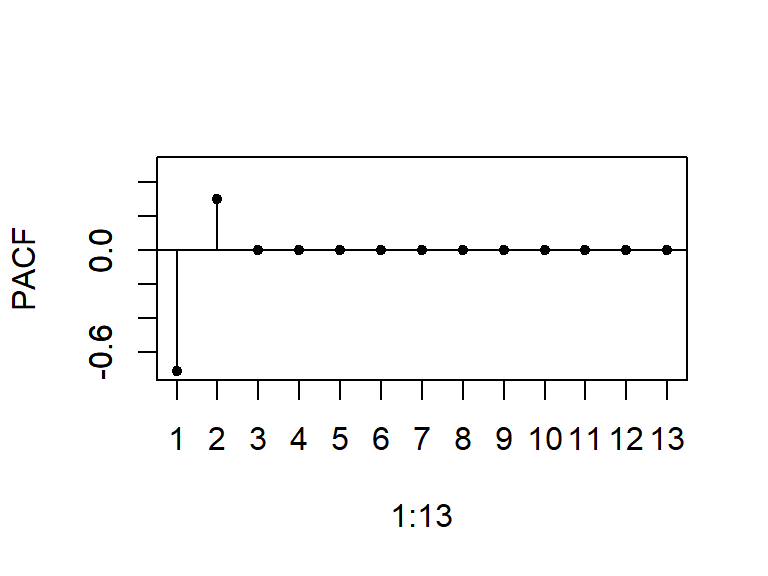
MA(1) y MA(2)

Contenido

Modelos ARIMA
AR(1) y AR(2)
MA(1) y MA(2)
ARMA(1,1)

MA(1)

El MA(1), modelo no estacional de medias móviles de orden 1, está definido por el siguiente proceso estocástico lineal: \[Z_t=C+a_t-\theta_1 a_{t-1}\] donde \(C\) y \(\theta_1\) son constantes desconocidas, y \(a_t \sim wn(0,\sigma_a^2)\).

Como \(E(a_t)=0\) para todo \(t\), \[\mathbb{E}(Z_t)=C~~ \text{es independiente de} ~t.\]
\[\mathrm{Var}(Z_t)= \mathrm{Var}(a_t)+\theta_1^2 \mathrm{Var}(a_{t-1})=\sigma_a^2+\theta_1^2 \sigma_a^2=\sigma_a^2(1+\theta_1^2)~~ \text{es finito e independiente de} ~t.\]
La función de autocovariancia es:

\[\begin{aligned} \gamma_Z(t, t-k) &= \mathrm{Cov}(Z_t, Z_{t-k}) = \mathbb{E} \left[ (Z_t - C)(Z_{t-k} - C) \right] \\ &= \mathbb{E} \left[ (a_t - \theta_1 a_{t-1})(a_{t-k} - \theta_1 a_{t-k-1}) \right] \\ &= \begin{cases} -\theta_1 \sigma_a^2, & \text{if } k = 1 \\ 0, & \text{if } k > 1 \end{cases} \end{aligned}\]

Note que MA(1) es siempre estacionario independiente del valor de \(\theta\).

Sin embargo, es necesario aplicar la restricción \(|\theta_1|<1\).
Note que a partir de \(Z_t=C+a_t-\theta_1 a_{t-1}\), se puede despejar \(a_t\), \[-C+Z_t+\theta_1 a_{t-1}=a_t.\] Esta misma ecuación cumple para \(t-1\): \[-C+Z_{t-1}+\theta_1 a_{t-2}=a_{t-1}.\] Podemos sustituirla recursivamente: en el modelo \[Z_t=C+a_t-\theta_1 \left[ -C+Z_{t-1}+\theta_1 a_{t-2} \right],\] y obtener: \[Z_t=C(1+\theta_1+\theta_1^2+...)-\theta_1 Z_{t-1}-\theta_1^2 Z_{t-2}-\theta_1^3 Z_{t-3}-...+a_t\]
Si \(|\theta_1|\geq 1\), la ecuación anterior implica que \(Z_t\) depende más a los valores pasados lejanos que los valores cercanos, lo cual no es realista en su interpretación. Esta condición es conocida como condición de invertibilidad.

La función de autocorrelación del proceso MA(1) es:

\[\begin{aligned} \rho_1 &= \frac{\mathrm{Cov}(Z_t, Z_{t-1})}{\sqrt{\mathrm{Var}(Z_t)\mathrm{Var}(Z_{t-1})}} = \frac{\mathrm{Cov}(Z_t, Z_{t-1})}{\mathrm{Var}(Z_t)} \\ &= \frac{-\theta_1 \sigma_a^2}{\sigma_a^2(1 + \theta_1^2)} = \frac{-\theta_1}{1 + \theta_1^2}, ~~\text{y} \\ \rho_k &= 0, \quad \text{para } k \geq 2 \end{aligned}\]

La función de autocorrelación teórica de MA(1) cae bruscamente a cero después del rezago 1.

Se puede demostrar que la función de autocorrelación parcial está dada por: \[\rho_{kk}=\frac{-\theta_1^k (1-\theta_1^2)}{1-\theta_1^{2(k+1)}},~~\text{para}~k \geq 1.\]
La PACF decae a cero de forma exponencial amortiguada.

La ACF y PACF teórica de un MA(1):

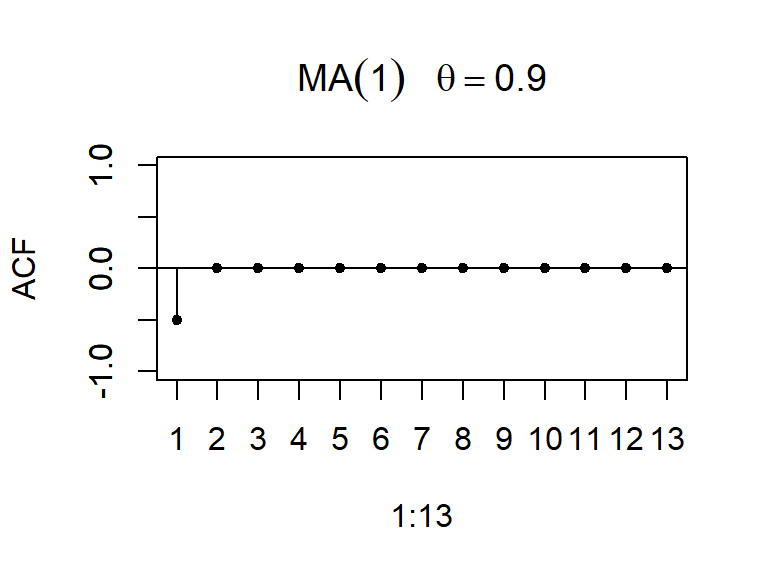
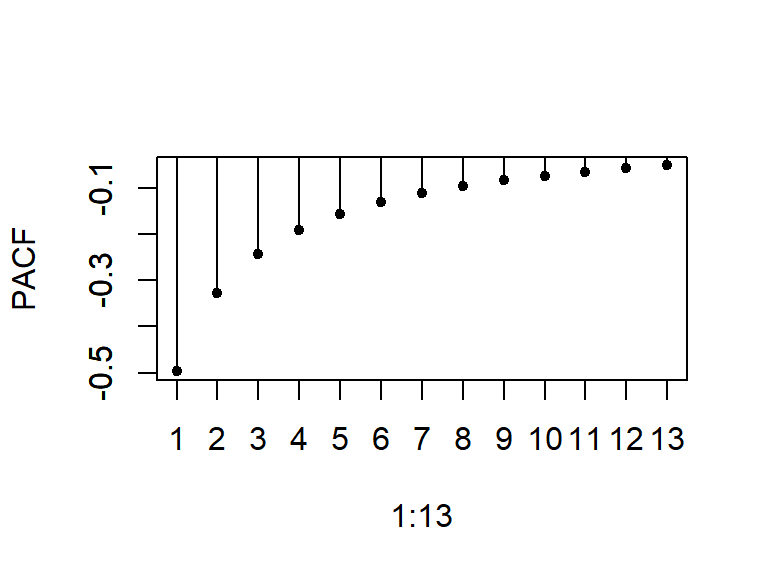
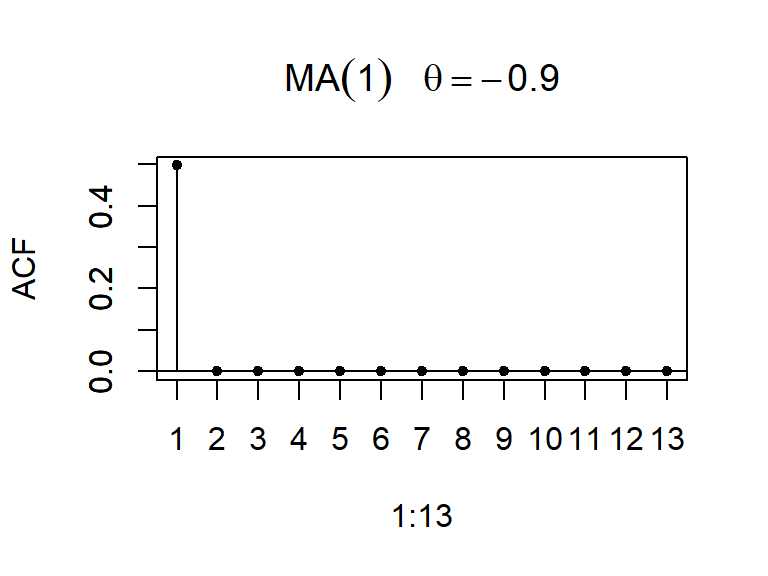
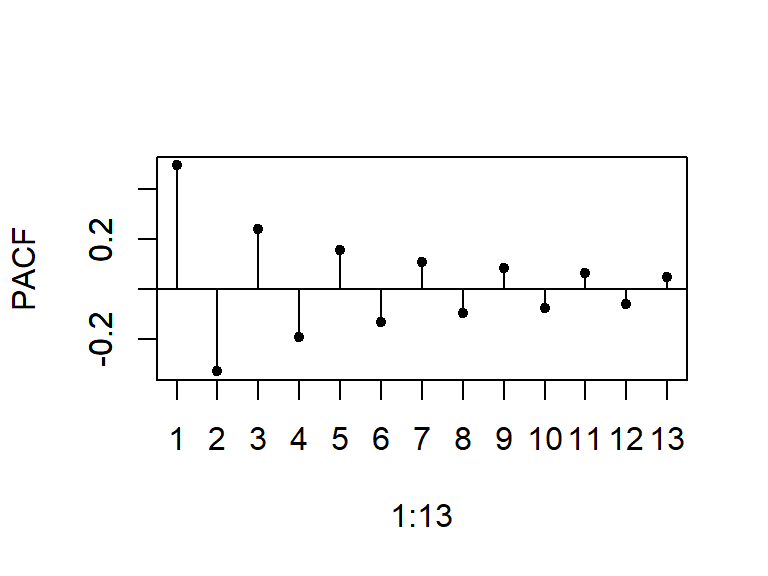
Considere dos simulaciones de un modelo MA(1)

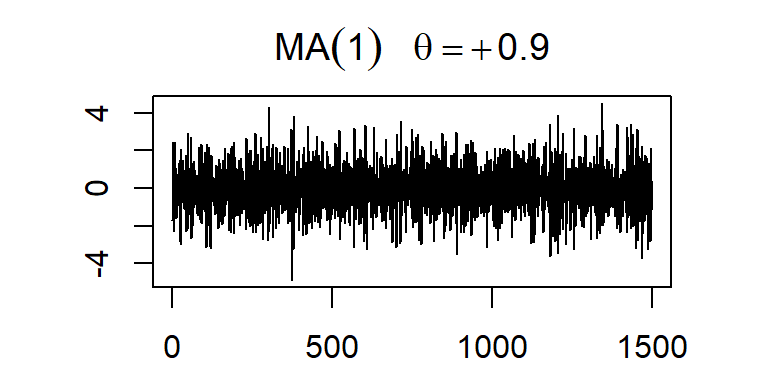
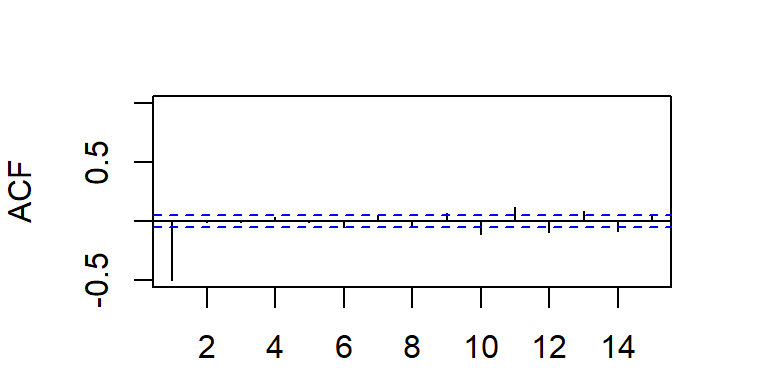
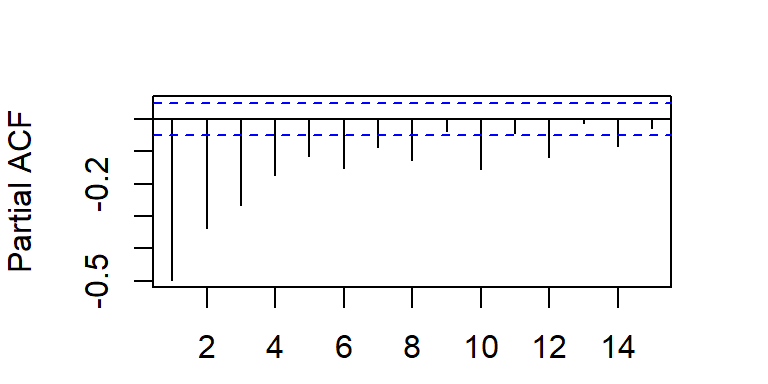
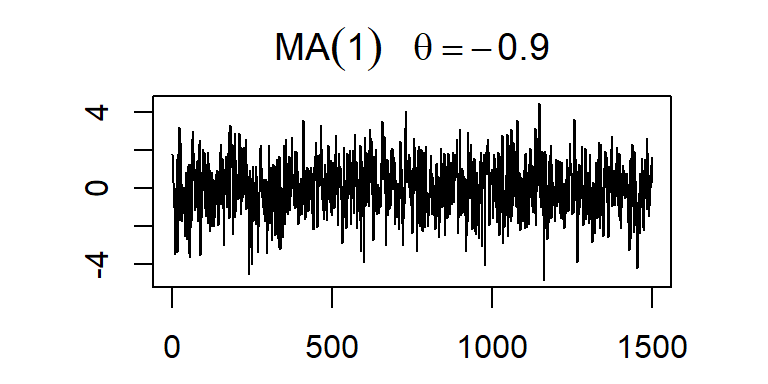
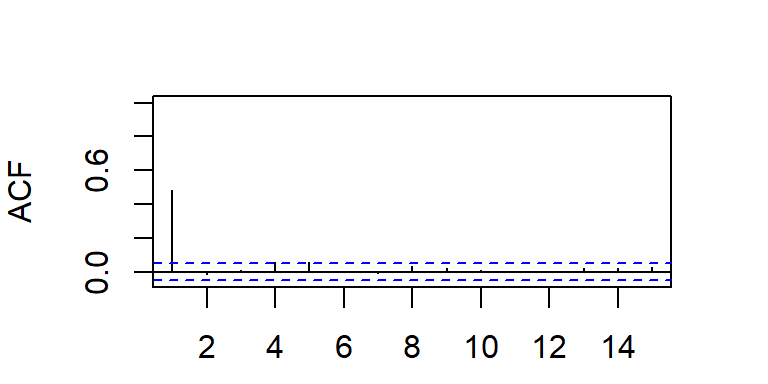
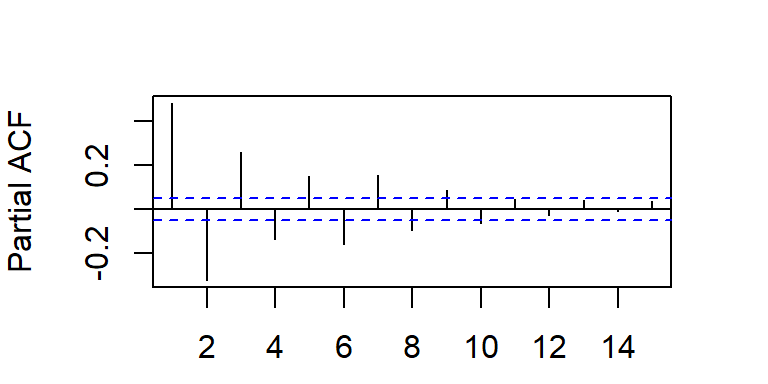
MA(2)

El modelo no estacional de medias móviles de orden 2, MA(2), está definido por el siguiente proceso estocástico lineal:

\[Z_t=C+a_t-\theta_1 a_{t-1}-\theta_2 a_{t-2}\] donde \(C\), \(\theta_1\) y \(\theta_2\) son constantes desconocidas, y \(a_t \sim wn(0,\sigma_a^2)\).

Se puede demostrar que MA(2) es estacionario para todo \(\theta_1\) y \(\theta_2\), con:

\(E(Z_t)=C\).
\(Var(Z_t)=\sigma_a^2(1+\theta_1^2+\theta_2^2)\).

La función de autocorrelación está dada por:

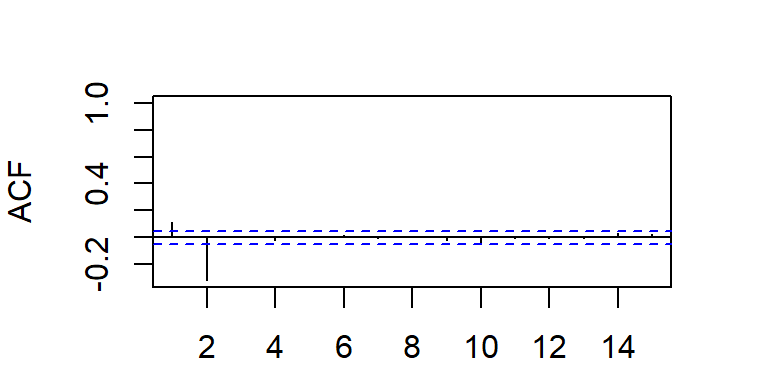
\[ \rho_k=\left\lbrace \begin{aligned} \frac{-\theta_1 (1-\theta_2) }{1+\theta_1^2+\theta_2^2}, & & k = 1 \\ \frac{-\theta_2}{1+\theta_1^2+\theta_2^2} & & k=2 \\ 0, & & k \geq 3 \\ \end{aligned} \right. \]

La función de autocorrelación parcial decae a cero según una combinación de exponenciales amortiguadas y/o ondas sinusoidales amortiguadas.
El proceso MA(2) es invertible si: \[|\theta_2|<1\] \[\theta_1+\theta_2<1\] \[\theta_2-\theta_1<1\]

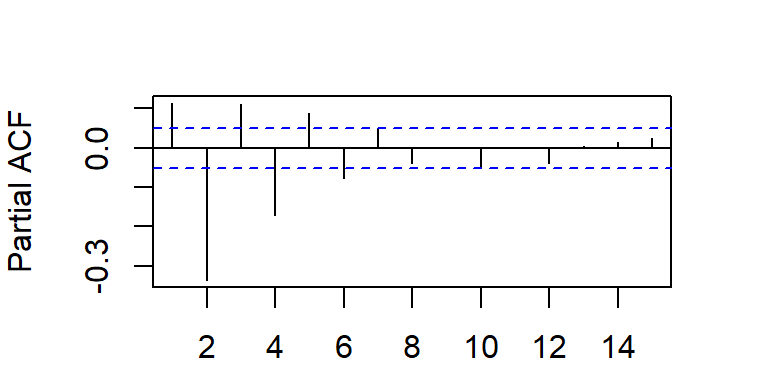
La ACF y PACF teórica y empírica de un modelo MA(2)

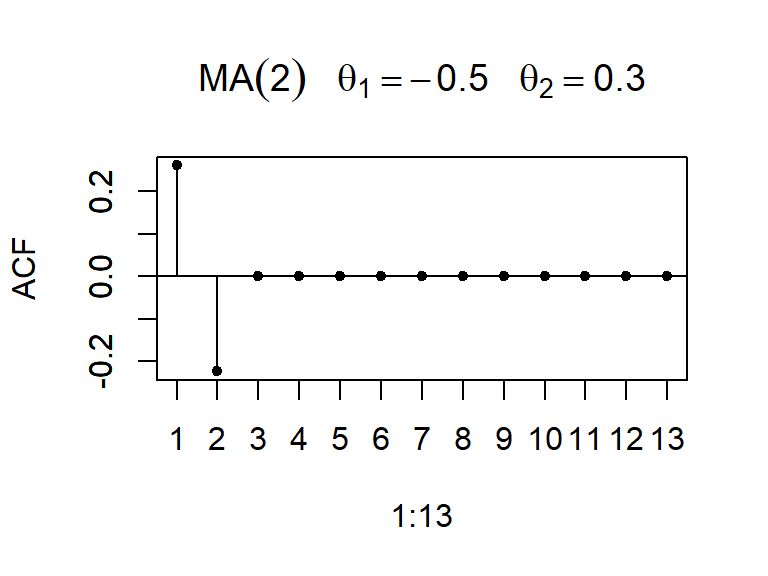
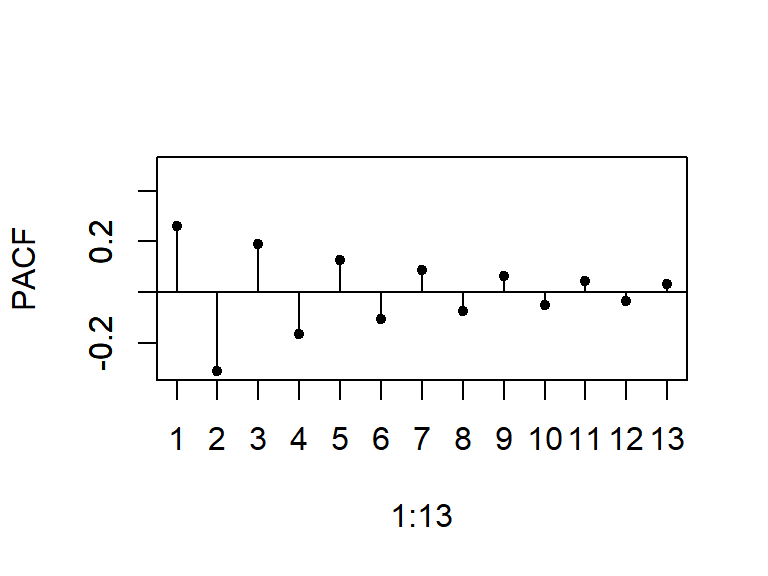
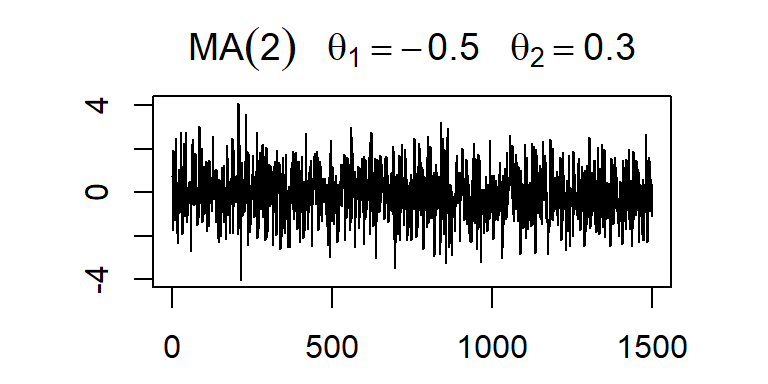
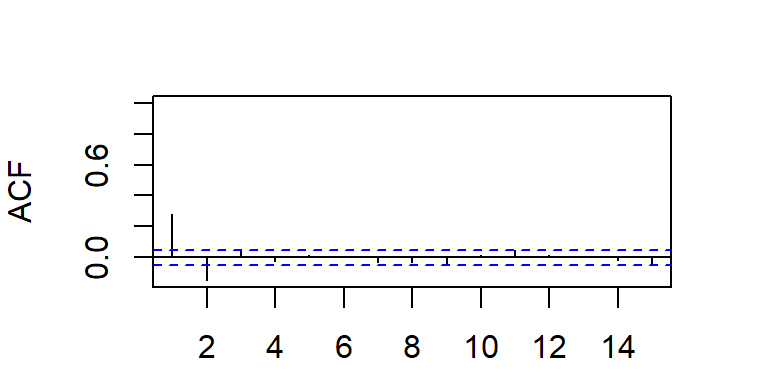
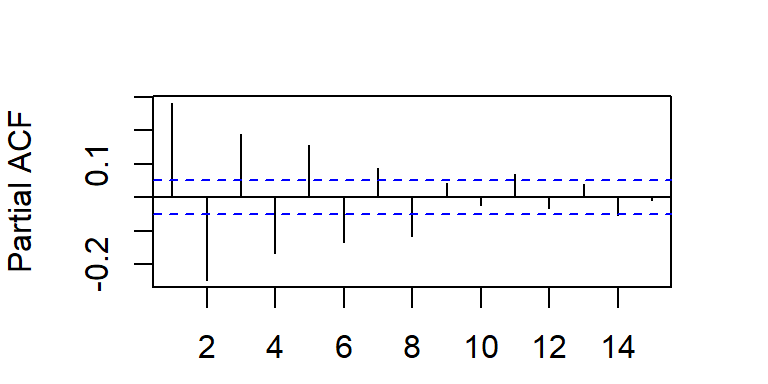
La ACF y PACF teórica y empírica de un modelo MA(2)

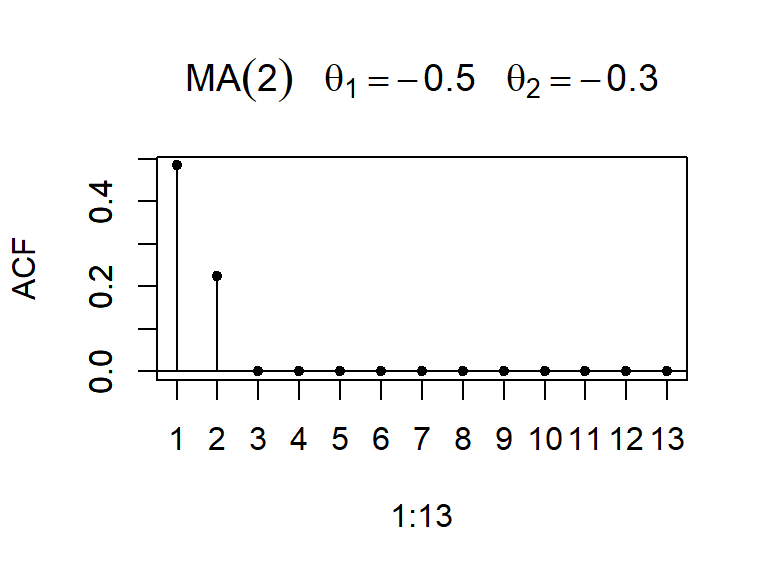
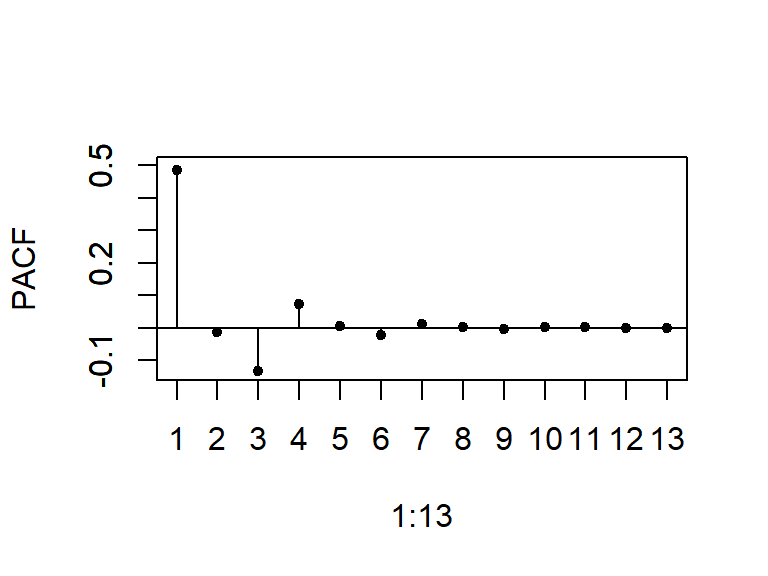
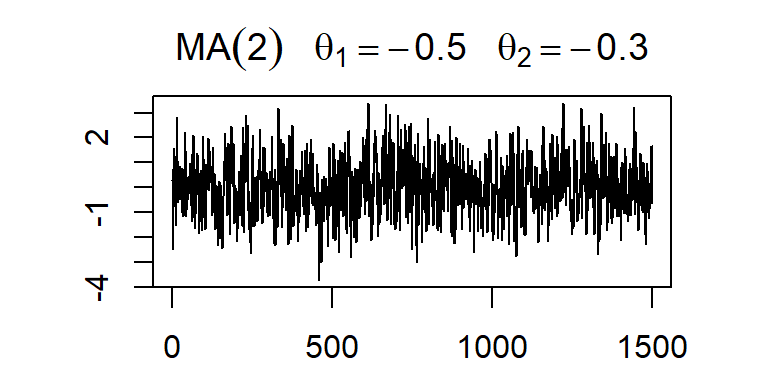
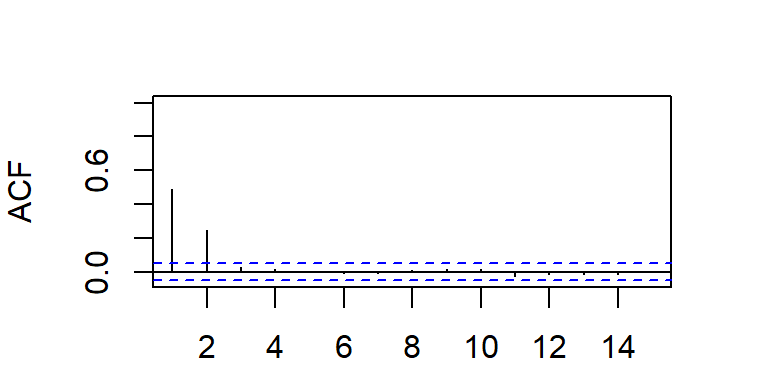
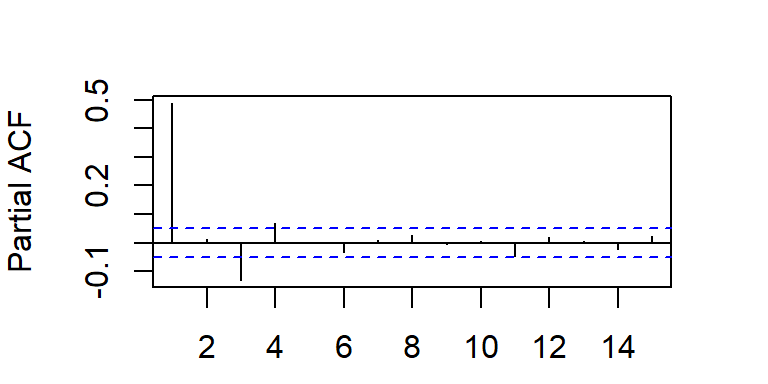
La ACF y PACF teórica y empírica de un modelo MA(2)

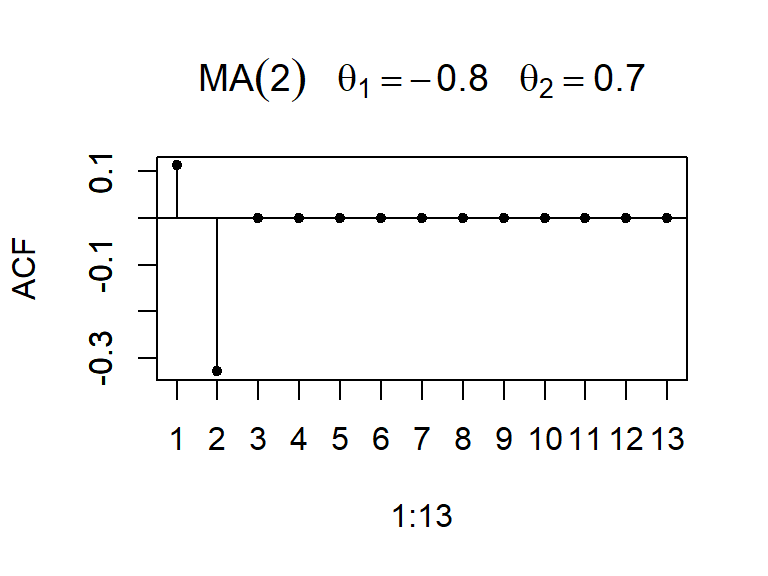
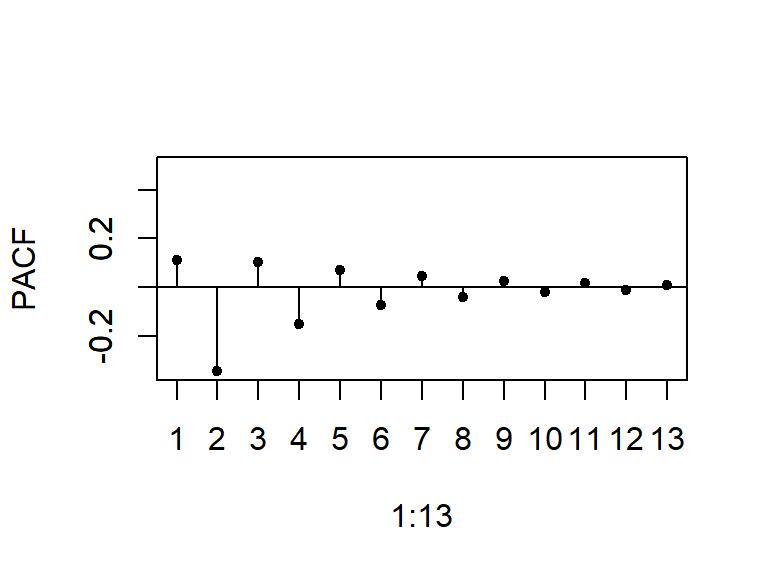
ARMA(1,1)

Contenido

Modelos ARIMA
AR(1) y AR(2)
MA(1) y MA(2)
ARMA(1,1)

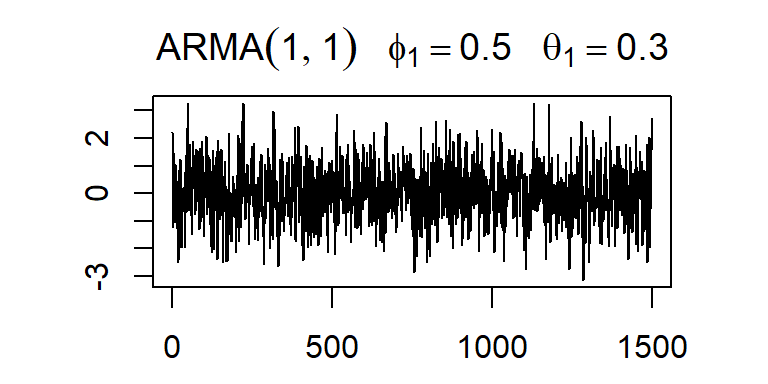
ARMA(1,1)

El ARMA(1,1) está definido por el siguiente proceso estocástico lineal: \[Z_t=C+a_t+\phi_1 Z_{t-1}-\theta_1 a_{t-1}\] o \[Z_t-\phi_1 Z_{t-1}=C+a_t-\theta_1 a_{t-1}\]

donde \(C\), \(\phi_1\) y \(\theta_1\) son constantes desconocidas, y \(a_t \sim wn(0,\sigma_a^2)\).

Condición de estacionariedad: \[|\phi_1|<1\]

Condición de invertibilidad: \[|\theta_1|<1\]

Con las condiciones de estacionariedad e invertibilidad, se puede mostrar que:

\[\mathbb{E}(Z_t)=\frac{C}{1-\phi_1}, ~~ \text{y}~~\mathrm{Var}(Z_t)=\frac{(1+ 2\theta_1 \phi_1+\theta_1^2)}{1-\phi_1^2} \sigma_a^2.\]

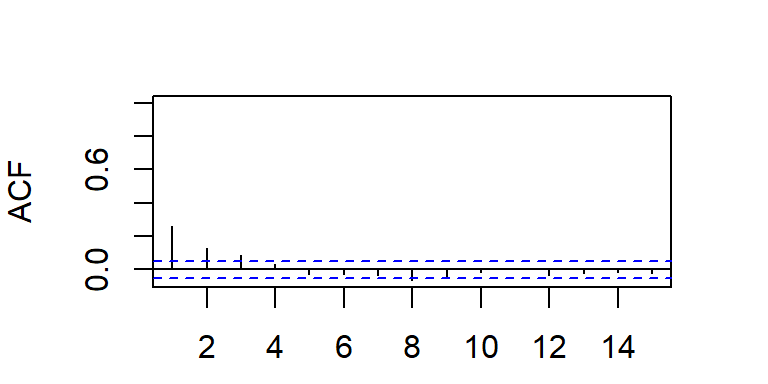
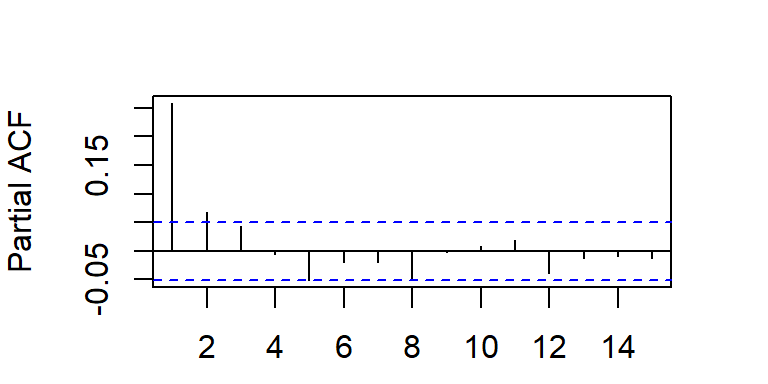
La función de autocorrelación teórica:

\[\rho_1=\frac{(1-\phi_1 \theta_1) (\phi_1-\theta_1)}{1+\theta_1^2-2\theta_1 \phi_1}\]

\[\rho_k=\phi_1 \rho_{k-1},~~~\text{para}~ k \geq 2,\] la cual decae de forma exponencial amortiguado desde el rezago 1.

Se puede demostrar que la función de autocorrelación parcial teórica decae de forma exponencial amortiguado desde el rezago 1 también.

La ACF y PACF teórica y empírica de un ARMA(1,1).

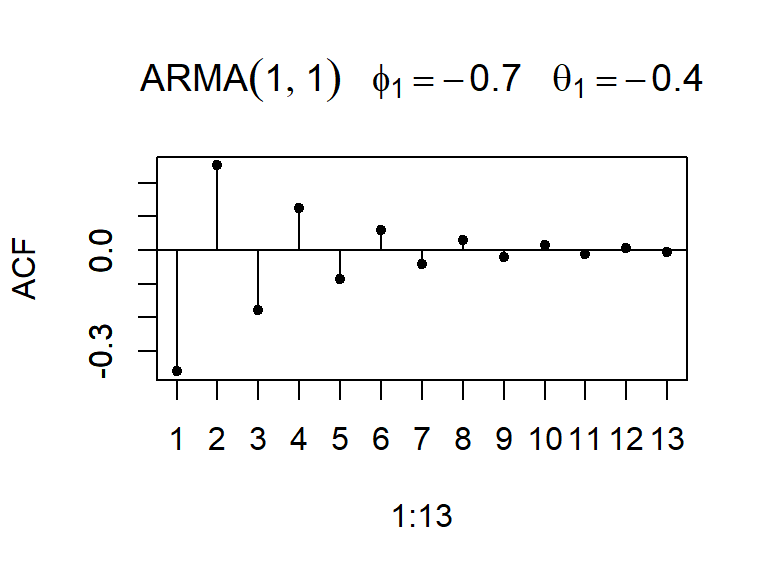
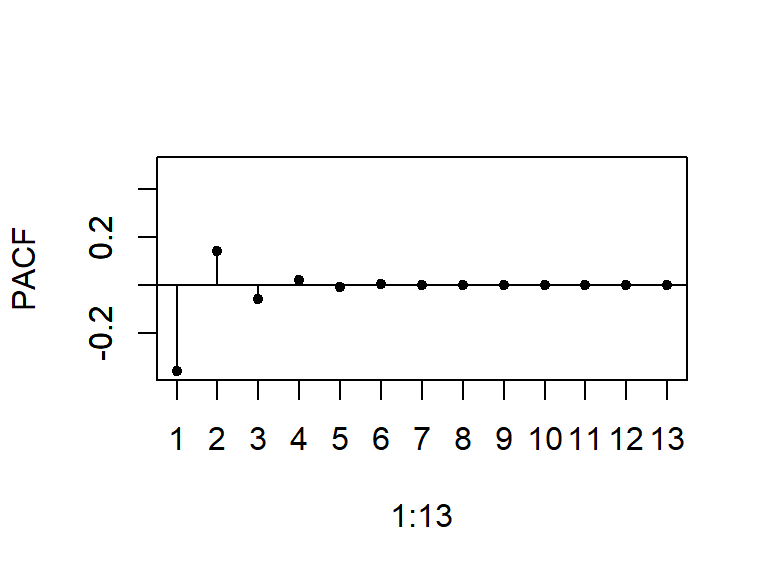
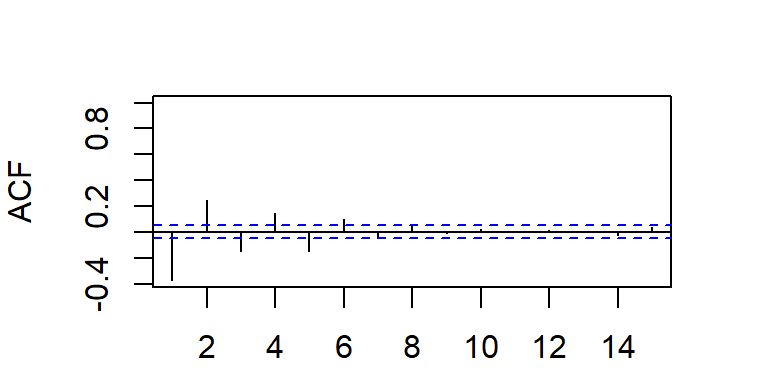
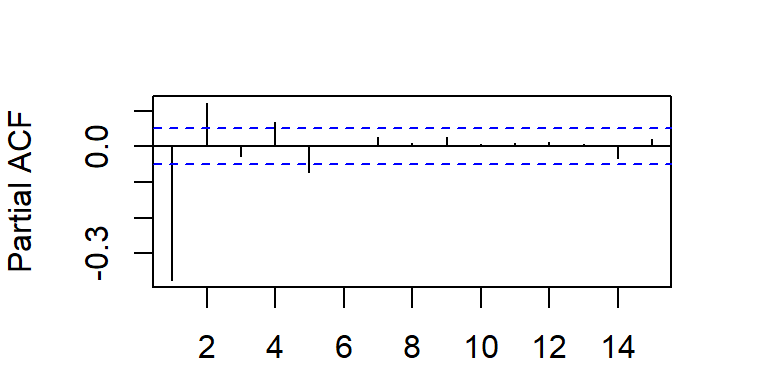
La ACF y PACF teórica y empírica de un ARMA(1,1).

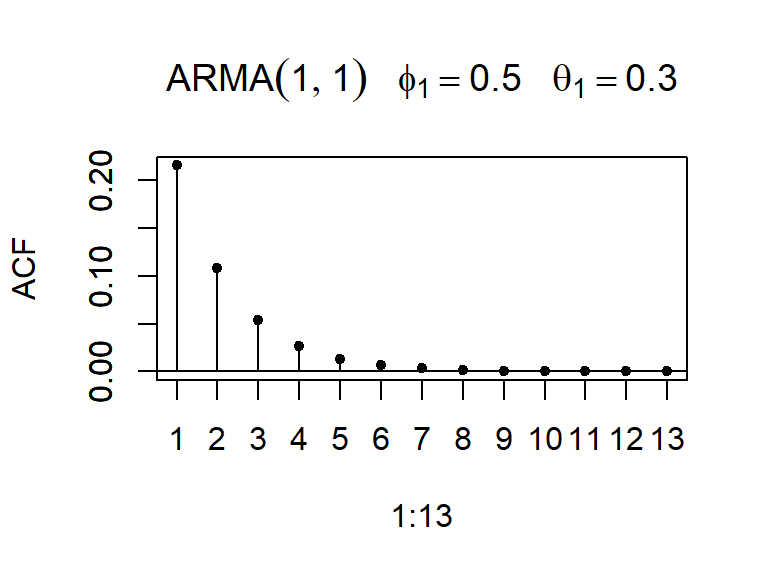
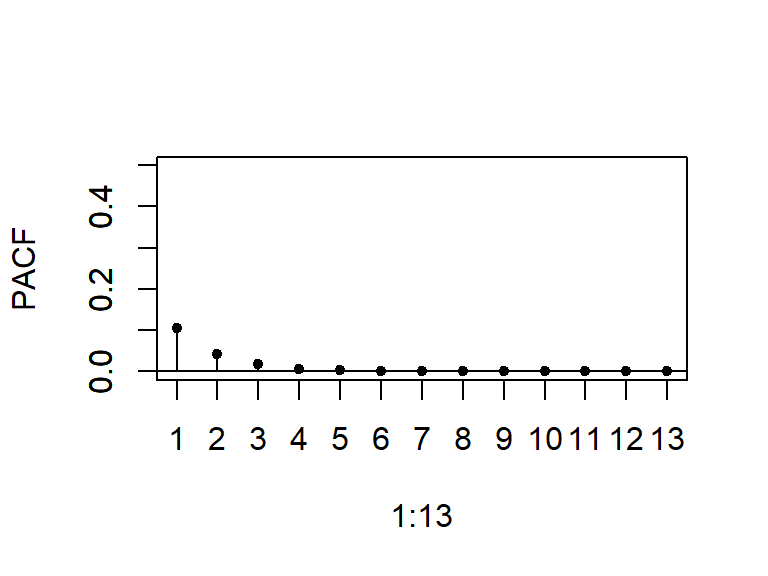
Note que el modelo ARMA(1,1) se puede reescribir como:

\[\begin{aligned} Z_t - \phi_1 Z_{t-1} &= C + a_t - \theta_1 a_{t-1} \\ &= \mathbb{E}(Z_t)(1 - \phi_1) + a_t - \theta_1 a_{t-1} \\ \Rightarrow \left[ Z_t - \mathbb{E}(Z_t) \right] - \phi_1 \left[ Z_{t-1} - \mathbb{E}(Z_t) \right] &= a_t - \theta_1 a_{t-1} \\ \Rightarrow \tilde{Z}_t - \phi_1 \tilde{Z}_{t-1} &= a_t - \theta_1 a_{t-1} \end{aligned}\]

donde \(\tilde{Z_t} = Z_t - E(Z_t)= Z_t - \mu_Z\).

Tabla de resumen 1

Modelo	Condición de estacionariedad	Condición de invertibilidad	ACF	PACF
AR(1)	\(\|\phi_1\|<1\)		Decae hacia cero según una combinación de exponenciales y/o ondas sinusoidales amortiguadas.	1 rezago
AR(2)	\(\|\phi_2\|<1\). \(\phi_1+\phi_2<1\). \(-\phi_1+\phi_2<1\).			2 regagos
MA(1)		\(\|\theta_1\|<1\)	1 rezago	Decae hacia cero según una combinación de exponenciales y/o ondas sinusoidales amortiguadas.
MA(2)		\(\|\theta_2\|<1\) \(\theta_1+\theta_2<1\) \(-\theta_1+\theta_2<1\)	2 regagos
ARMA(1,1)	\(\|\phi_1\|<1\)	\(\|\theta_1\|<1\)	Decae de forma exponencial amortiguado desde el rezago 1	Decae de forma exponencial amortiguado desde el rezago 1

Próximo tema

Modelos ARIMA de Box&Jenkins - Parte 2

AR(p)
MA(q)
ARMA(p,q)
ARIMA(p,d,q)

Tema 6: Modelos ARIMA de Box&Jenkins(1)

Paquetes de R

Modelos ARIMA

Modelos ARIMA

AR(1) y AR(2)

AR(1)

AR(2)

La función de autocorrelación parcial

ACF y PACF teórica y empírica de un AR(1)

La ACF y PACF teórica y empírica de un AR(2)

MA(1) y MA(2)

MA(1)

MA(2)

ARMA(1,1)

ARMA(1,1)

Tabla de resumen 1

Próximo tema

Modelos ARIMA de Box&Jenkins - Parte 2

Tema 6: Modelos ARIMA de Box&Jenkins⁽¹⁾