Tema 6: Modelos ARIMA de Box&Jenkins⁽²⁾

shuwei.chou@ucr.ac.cr

Escuela de Estadística, Universidad de Costa Rica

Paquetes de R

Para este tema, se necesita cargar estos paquetes:

library(ggplot2)
library(forecast)
library(fpp2)
library(astsa)

Tabla de resumen 1

Modelo	Condición de estacionariedad	Condición de invertibilidad	ACF	PACF
AR(1)	\(\|\phi_1\|<1\)		Decae hacia cero según una combinación de exponenciales y/o ondas sinusoidales amortiguadas.	1 rezago
AR(2)	\(\|\phi_2\|<1\). \(\phi_1+\phi_2<1\). \(-\phi_1+\phi_2<1\).			2 regagos
MA(1)		\(\|\theta_1\|<1\)	1 rezago	Decae hacia cero según una combinación de exponenciales y/o ondas sinusoidales amortiguadas.
MA(2)		\(\|\theta_2\|<1\) \(\theta_1+\theta_2<1\) \(-\theta_1+\theta_2<1\)	2 regagos
ARMA(1,1)	\(\|\phi_1\|<1\)	\(\|\theta_1\|<1\)	Decae de forma exponencial amortiguado desde el rezago 1	Decae de forma exponencial amortiguado desde el rezago 1

MA(q)

Contenido

MA(q)
AR(p)
ARMA(p,q)
Operadores de rezagos
Operador de diferencia
ARIMA(p,d,q)

MA(q)

El Modelo no estacional de medias móviles de orden q, MA(q), está definido por el siguiente proceso estocástico lineal:

\[Z_t=C+a_t-\theta_1 a_{t-1}-\theta_2 a_{t-2}-...-\theta_q a_{t-q}\]

donde \(C\) y \(\theta_i, i=1,...,q\) son constantes desconocidas, y \(a_t \sim wn(0,\sigma_a^2)\).

Se puede demostrar que MA(q) es estacionario para todo \(\theta_i\) para \(i=1,...,q\), con:

\(\mathbb{E}(Z_t)=C=\mu\).
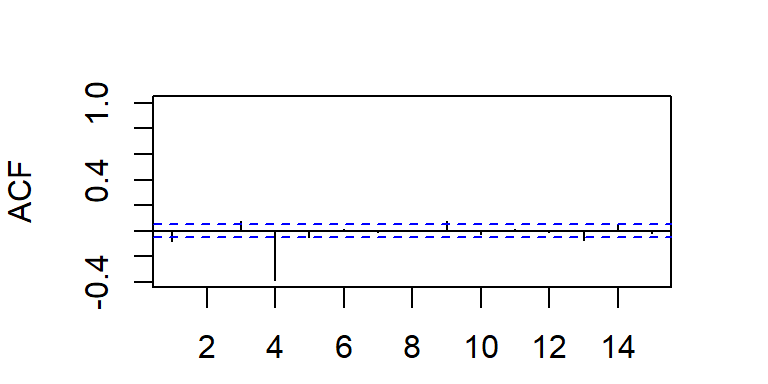
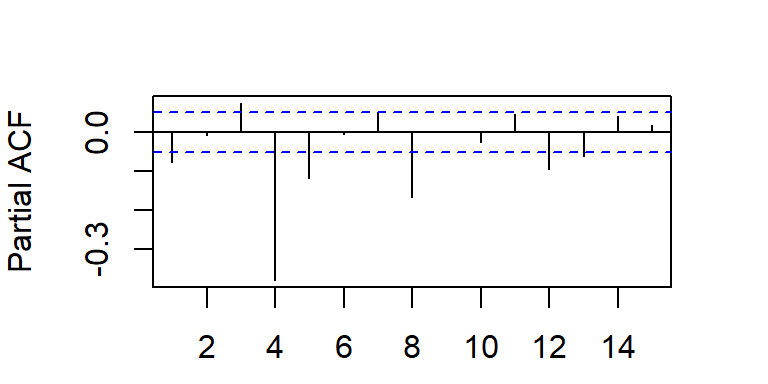
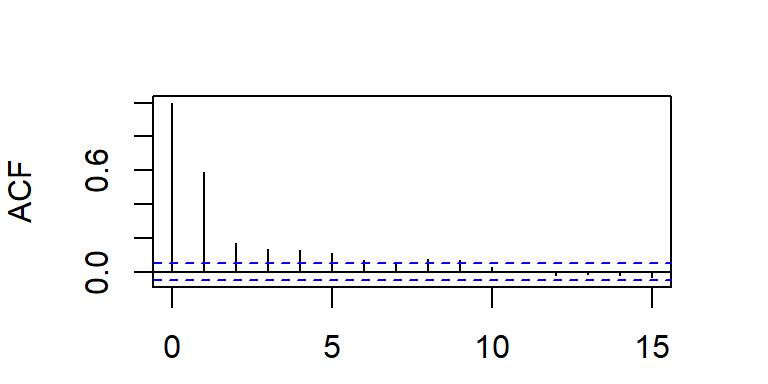
La ACF teórica tiene correlaciones no nulas en los rezagos \(1,...,q\) y ceros para rezagos mayores que \(q\), i.e.

\[\begin{align*} \rho_k &\neq 0 \quad \text{para } k = 1, \dots, q, \\ \rho_k &= 0 \quad \text{para } k > q. \end{align*}\]

La PACF decae a cero según una combinación de exponenciales amortiguadas y/o ondas sinusoidales amortiguadas.
MA(q) siempre es estacionario pero no es invertible (veremos los supuestos).

Considere \(a_t \sim N(0,1)\), y un modelo MA(q).

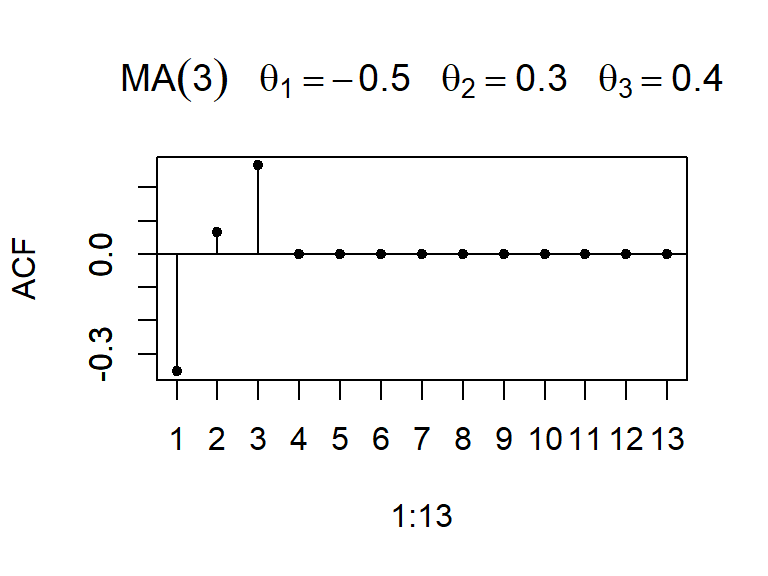
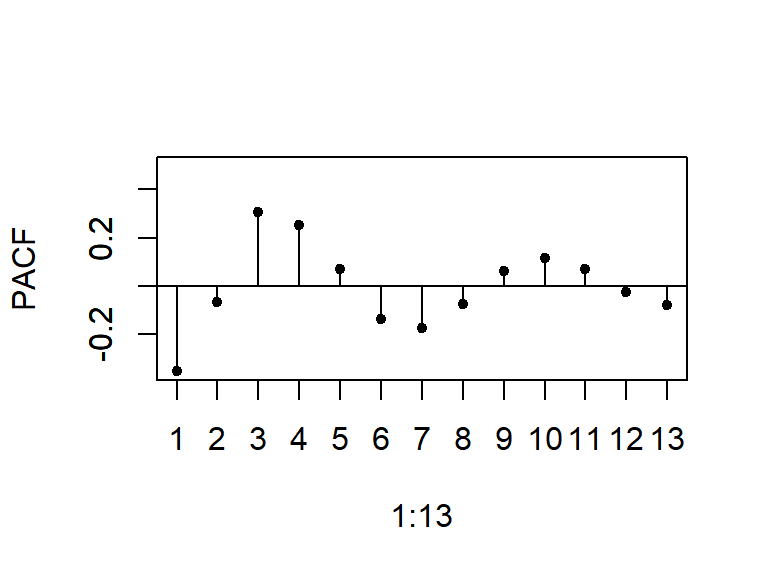
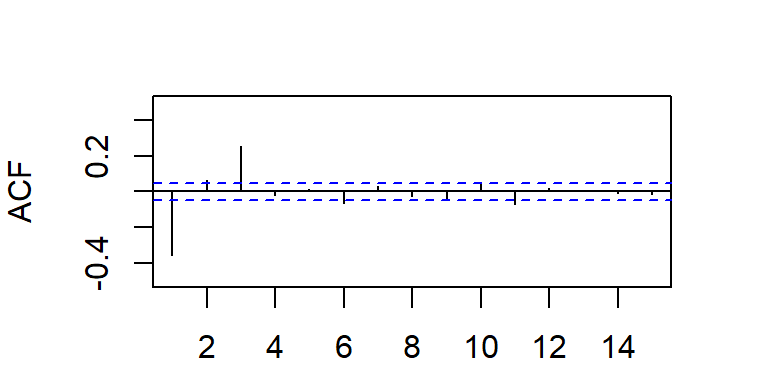
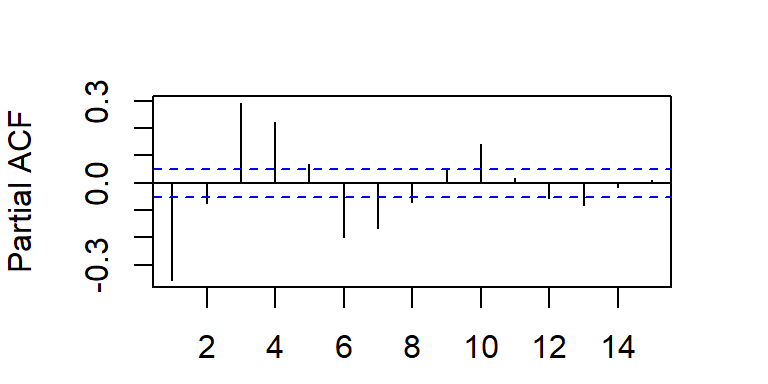
Considere \(a_t \sim N(0,1)\), y un modelo MA(q).

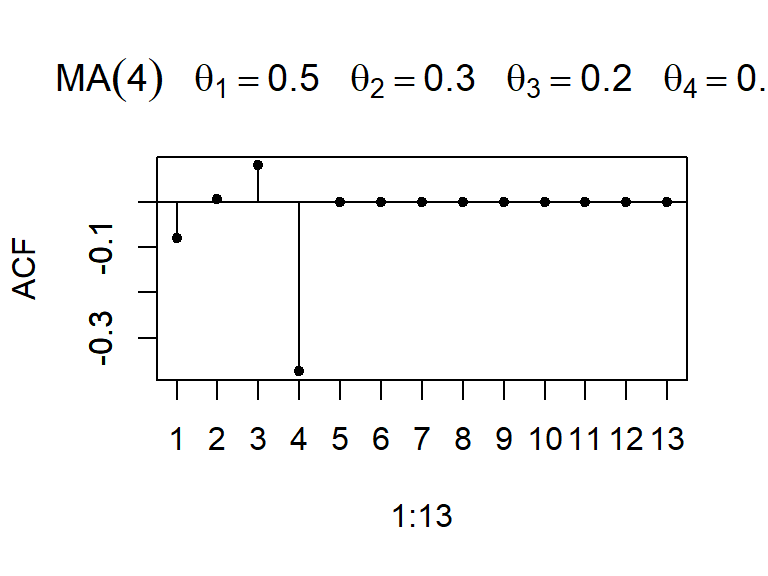
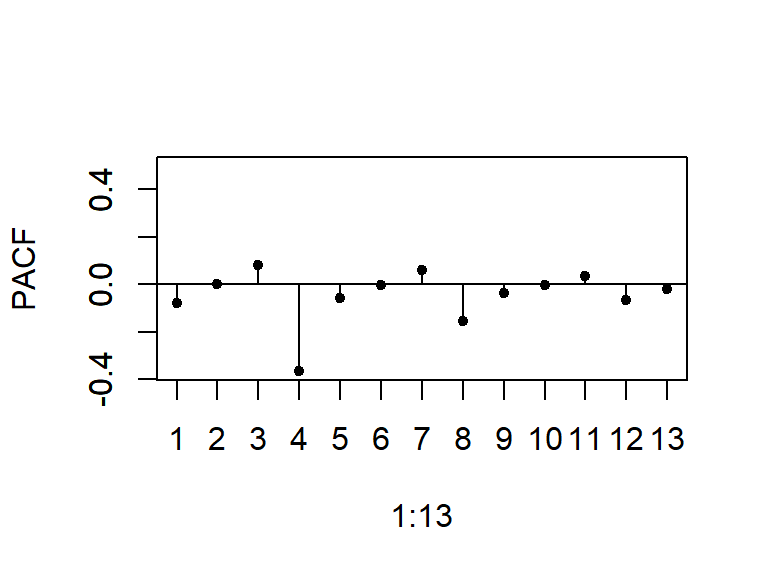
AR(p)

Contenido

MA(q)
AR(p)
ARMA(p,q)
Operadores de rezagos
Operador de diferencia
ARIMA(p,d,q)

AR(p)

El modelo no estacional autoregresivo de orden p, AR(p), está definido por el siguiente proceso estocástico lineal:

\[Z_t=C+\phi_1 Z_{t-1}+\phi_2 Z_{t-2}+...+\phi_p Z_{t-p}+a_t\] donde: \(C\) y \(\phi_i, i=1,...,p\) son constantes desconocidas, y \(a_t \sim wn(0,\sigma_a^2)\).

Se puede demostrar que:

\(\mathbb{E}(Z_t)= \frac{C}{1-\phi_1-\phi_2-...-\phi_p}=\mu\).
La ACF decae a cero según una combinación de exponenciales amortiguadas y/o ondas sinusoidales amortiguadas.
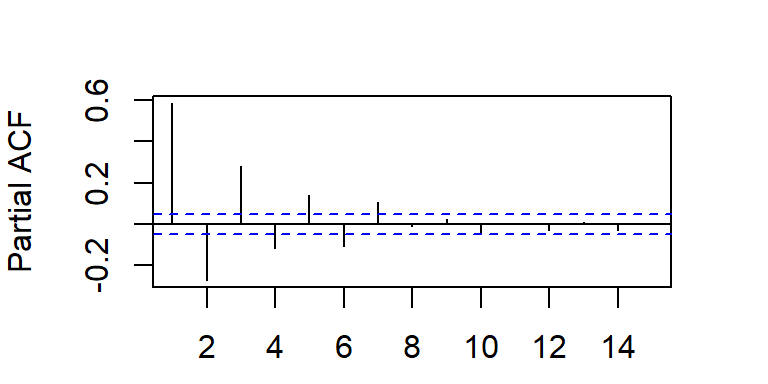
La PACF teórica tiene autocorrelaciones parciales no nulas en los rezagos \(1,...,p\) y ceros para rezagos mayores que \(p\), i.e. \[\begin{align*} \rho_{kk} &\neq 0 \quad \text{para } k = 1, \dots, p, \\ \rho_{kk} &= 0 \quad \text{para } k > p. \end{align*}\]
El AR(p) es invertible pero no es siempre estacionario (veremos las condiciones).

Considere \(a_t \sim N(0,1)\), y un modelo AR(p).

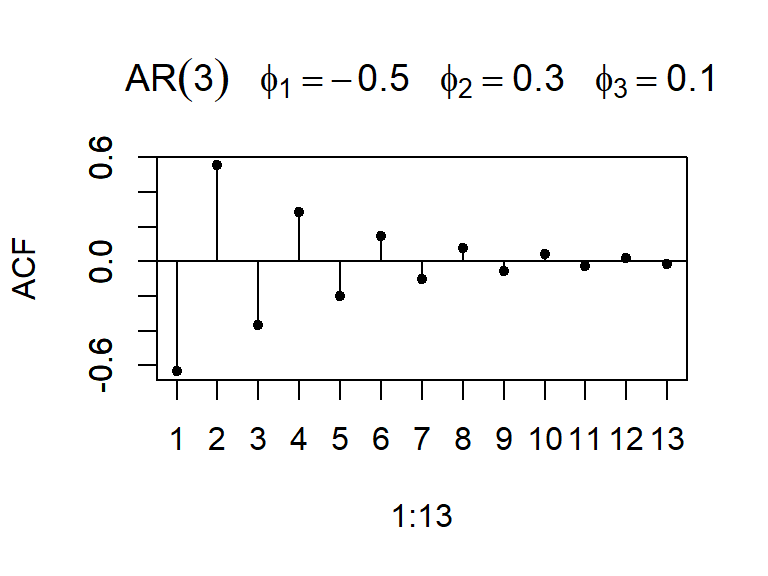
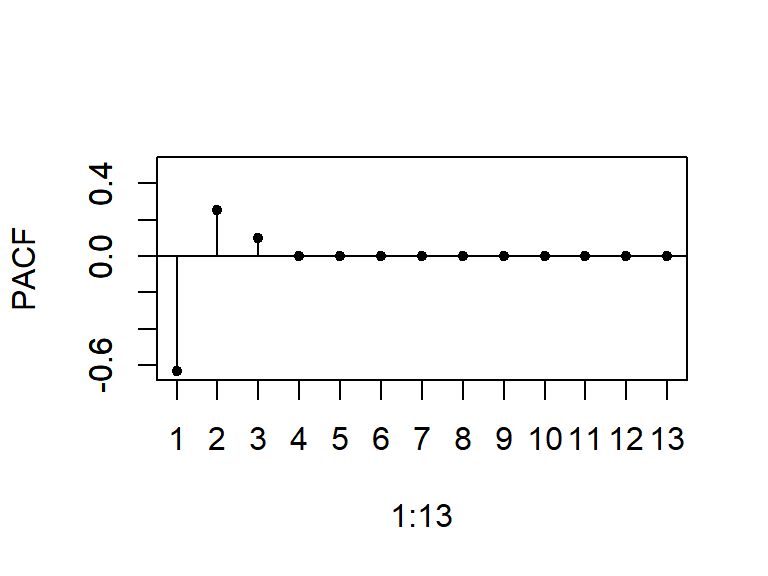
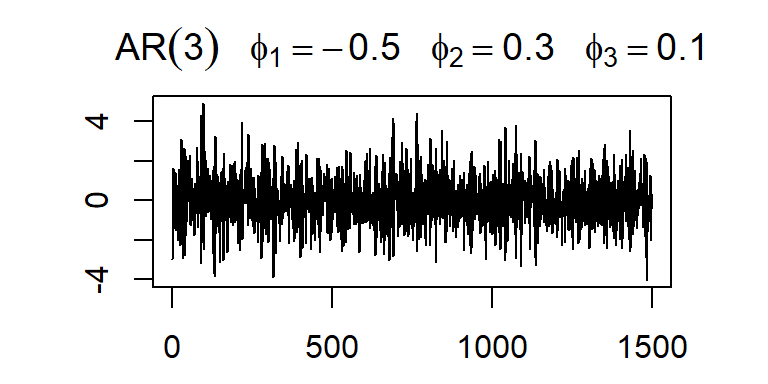
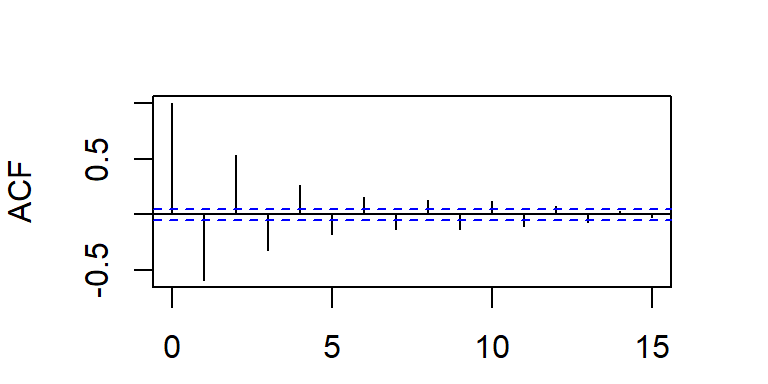
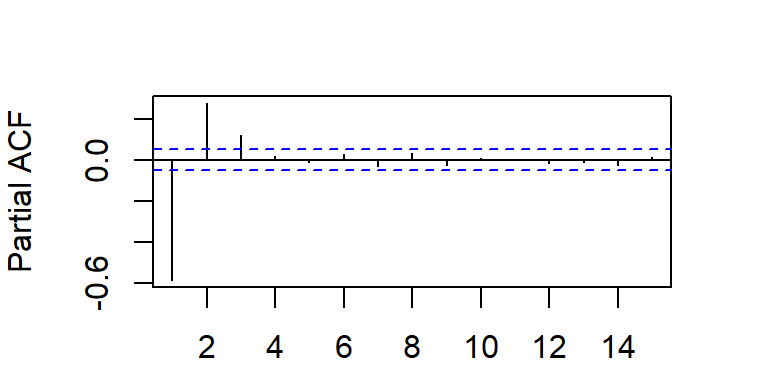
Considere \(a_t \sim N(0,1)\), y un modelo AR(p).

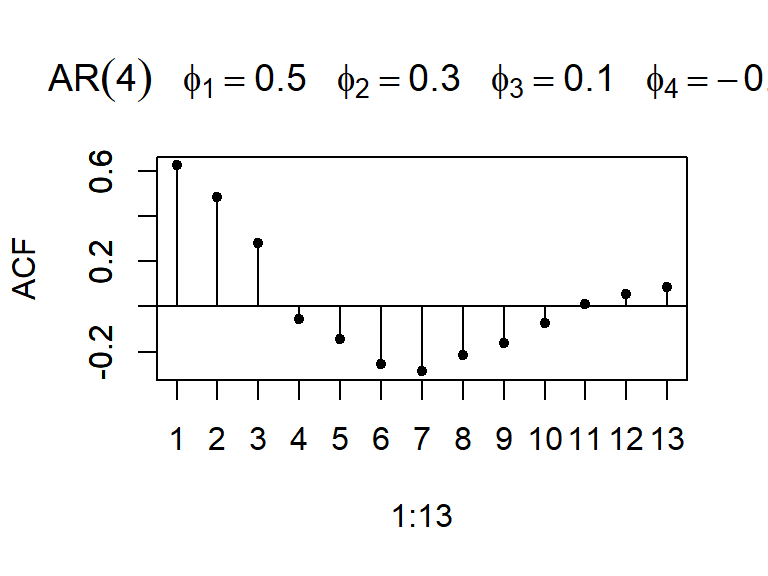
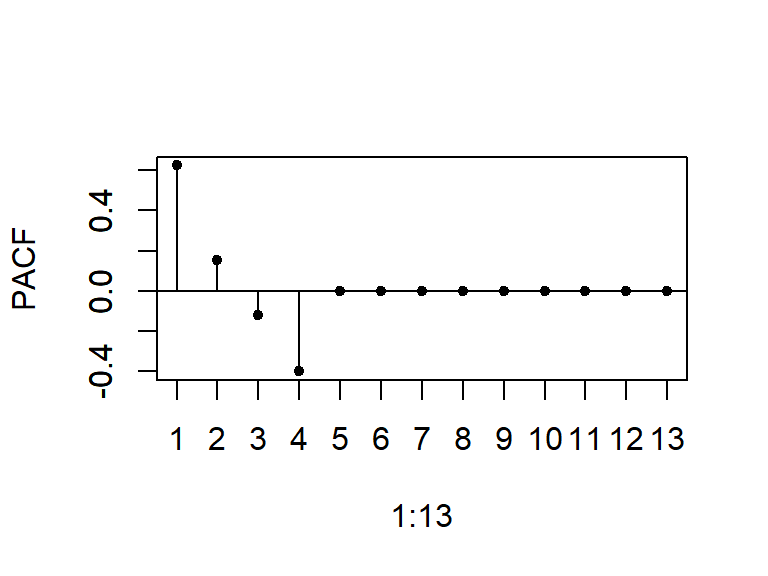
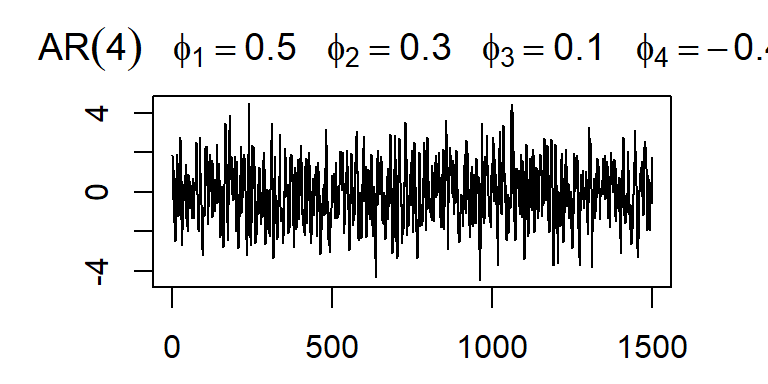
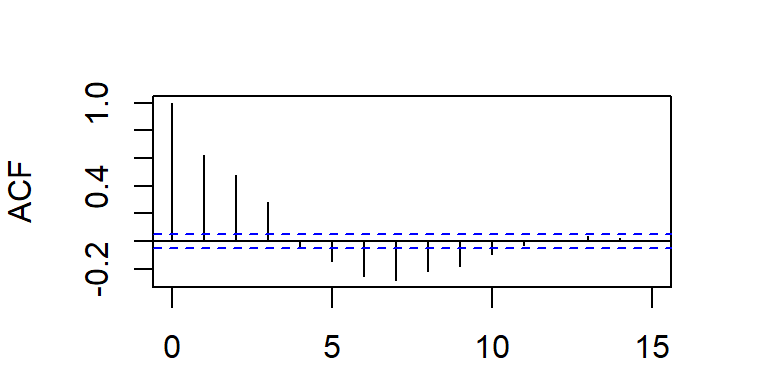
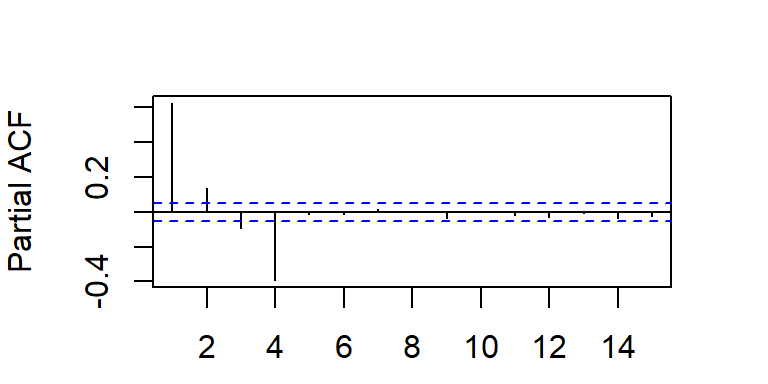
ARMA(p,q)

Contenido

MA(q)
AR(p)
ARMA(p,q)
Operadores de rezagos
Operador de diferencia
ARIMA(p,d,q)

ARMA(p,q)

El modelo mixto no estacional autoregresivo de medias móviles de orden \(p\) y \(q\), ARMA(p,q), está definido por el siguiente proceso estocástico lineal:

\[Z_t=C+\phi_1 Z_{t-1}+\phi_2 Z_{t-2}+...+\phi_p Z_{t-p}+a_t-\theta_1 a_{t-1}-\theta_2 a_{t-2}-...-\theta_q a_{t-q}\] donde \(C\), \(\phi_i, i=1,...,p\) y \(\theta_j, j=1,...,q\) son constantes desconocidas, y \(a_t \sim wn(0,\sigma_a^2)\) (independiente de \(Y_t\)).

Se puede demostrar que:

\(\mathbb{E}(Z_t)= \frac{C}{1-\phi_1-\phi_2-...-\phi_p}=\mu\).
La ACF decae a cero después de los primeros \(q-p\) según una combinación de exponenciales amortiguadas y/o ondas sinusoidales amortiguadas.
La PACF teórica decae a cero después de los primeros \(p-q\) según una combinación de exponenciales amortiguadas y/o ondas sinusoidales amortiguadas.
¿Condición de estacionariedad y invertibilidad? (veremos más adelante)

Considere \(a_t \sim N(0,1)\), y un modelo ARMA(2,1).

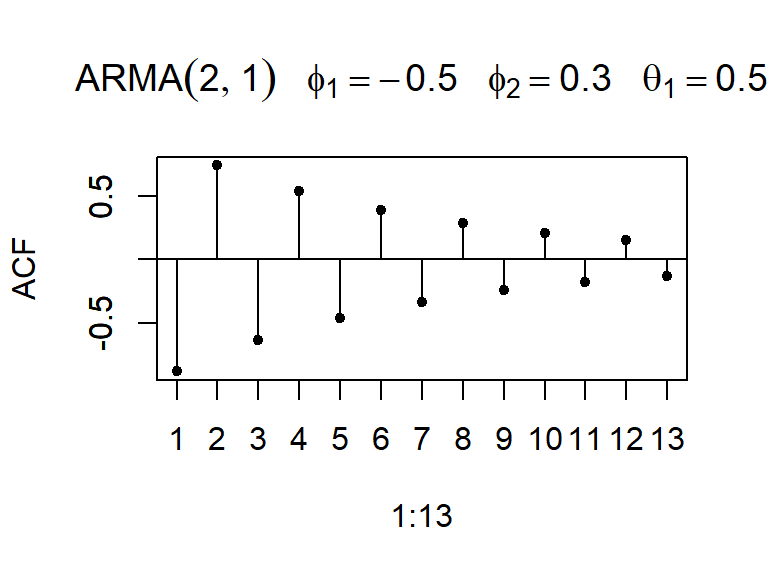
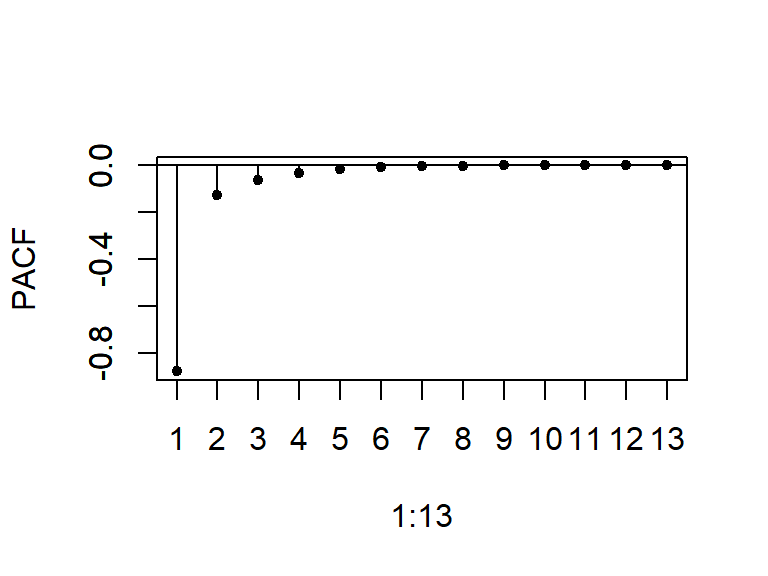
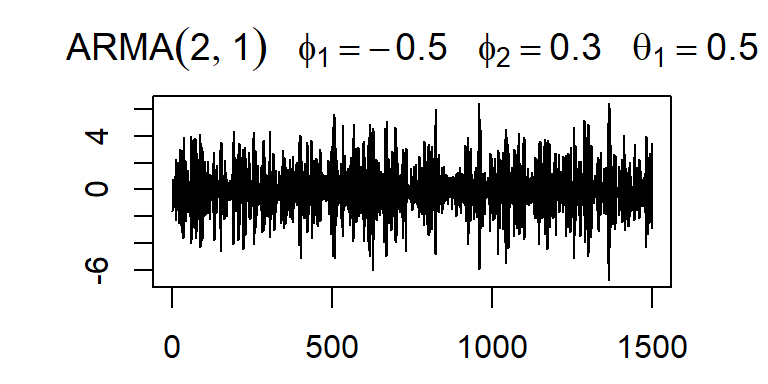
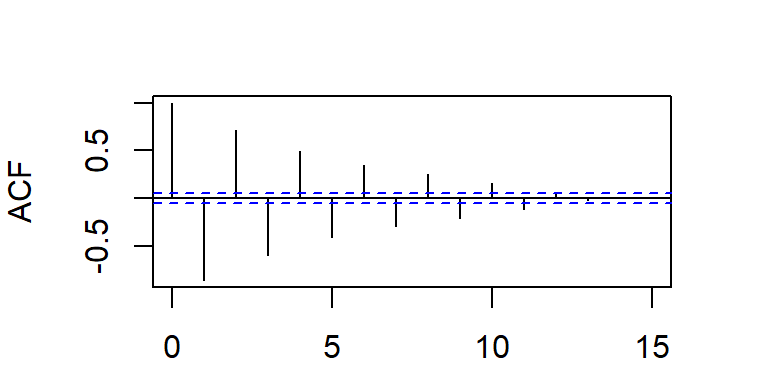
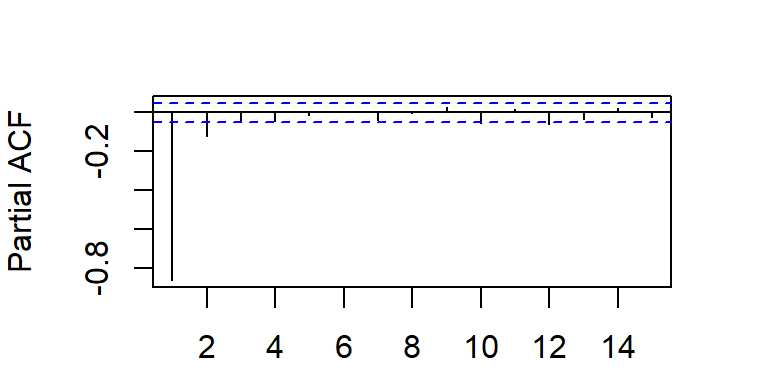
Considere \(a_t \sim N(0,1)\), y un modelo ARMA(1,2).

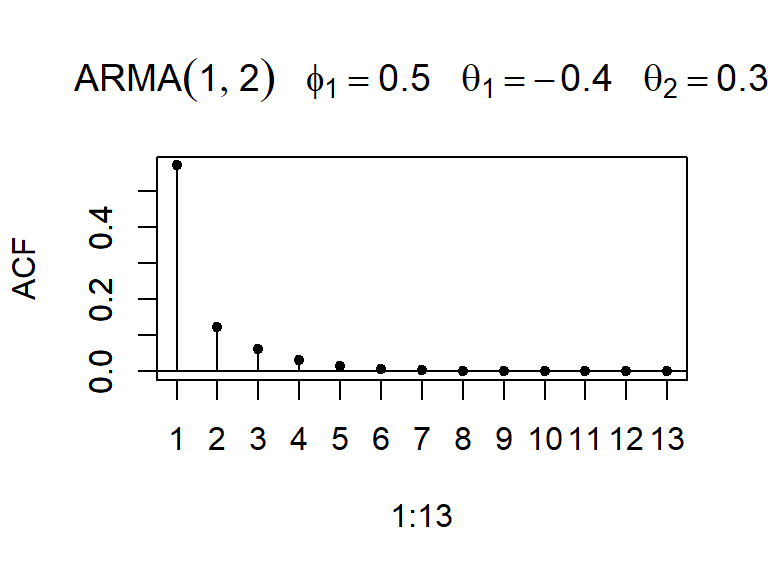
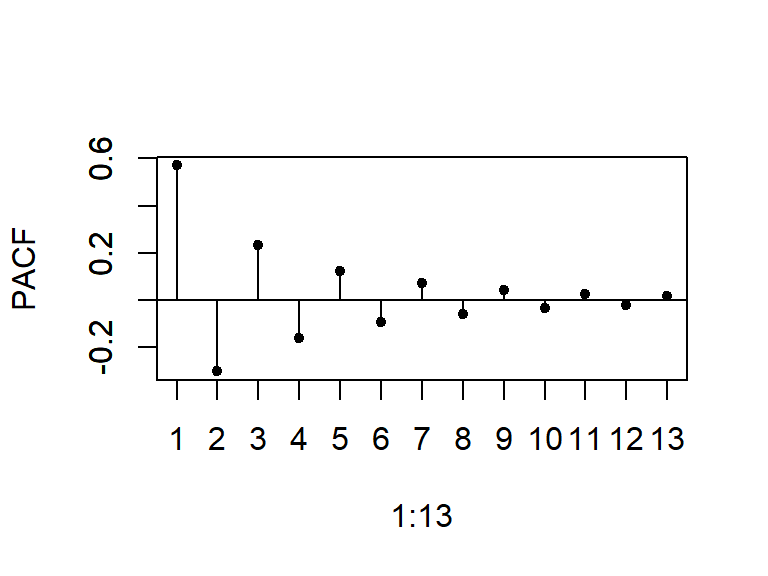
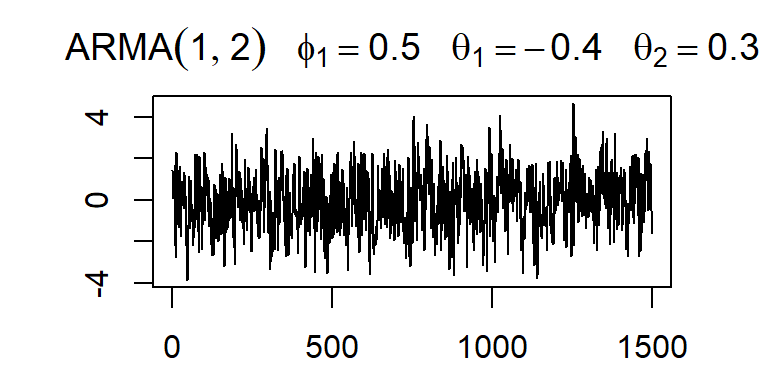
Operadores de rezagos

Contenido

MA(q)
AR(p)
ARMA(p,q)
Operadores de rezagos
Operador de diferencia
ARIMA(p,d,q)

Operadores de rezagos

El operador de rezago \(B\) es definido como \[B Z_t= Z_{t-1}\]
El operador de rezago \(B\) se puede volver a aplicar: \[B Z_{t-1} = Z_{t-2}=BBZ_{t}=B^2 Z_t\]
De esta forma, se puede extender el operador de rezago a: \[B^k Z_t = Z_{t-k}\]
También se puede definir el operador inverso \(B^{-1}\) de tal forma que \(B^{-1}B=1\), entonces \[B^{-1} Z_{t-1} = Z_{t}\]
\(B\) es llamado como operador de retroceso (backshift).
\(B^{-1}\) es llamado como operador de progreso (forward-shift).

Ejemplo con AR(2)

Note que:

\[\begin{align*} Z_t &= C + \phi_1 Z_{t-1} + \phi_2 Z_{t-2} + a_t \\ \Rightarrow\quad Z_t - \phi_1 Z_{t-1} - \phi_2 Z_{t-2} &= C + a_t \\ \Rightarrow\quad Z_t - \phi_1 Z_{t-1} - \phi_2 Z_{t-2} &= \mu (1 - \phi_1 - \phi_2) + a_t \end{align*}\]

ya que \(\mathbb{E}(Z_t)= \frac{C}{1-\phi_1-\phi_2}=\mu\).

Reordenando los términos, \[(Z_t-\mu)-\phi_1 (Z_{t-1}-\mu)-\phi_2 (Z_{t-2}-\mu)=a_t.\] Tome \(\tilde{Z}_t=Z_t-\mu\), \[\begin{align*} \tilde{Z}_t - \phi_1 \tilde{Z}_{t-1} - \phi_2 \tilde{Z}_{t-2} &= a_t \\ \tilde{Z}_t - \phi_1 B \tilde{Z}_t - \phi_2 B^2 \tilde{Z}_t &= a_t \\ (1 - \phi_1 B - \phi_2 B^2)\, \tilde{Z}_t &= a_t \end{align*}\]

Ejemplo con MA(2)

De la misma forma, el MA(2): \[Z_t=C+a_t-\theta_1 a_{t-1}-\theta_2 a_{t-2}\] se puede escribir como
\[\tilde{Z}_t=(Z_t-\mu)=(1-\theta_1 B-\theta_2 B^2)a_t\]

ARMA(p,q)

El ARMA(p,q):

\[Z_t=C+\phi_1 Z_{t-1}+\phi_2 Z_{t-2}+...+\phi_p Z_{t-p}+a_t-\theta_1 a_{t-1}-\theta_2 a_{t-2}-...-\theta_q a_{t-q}\]

se puede escribir como:

\[(1-\phi_1 B -\phi_2 B^2-...-\phi_p B^p)\tilde{Z}_t=(1-\theta_1 B-\theta_2 B^2-...-\theta_q B^q)a_t.\]

\[\phi(B)\tilde{Z}_t=\theta(B)a_t.\] donde:
\(\phi(B)=1-\phi_1 B -\phi_2 B^2-...-\phi_p B^p\) es el operador autoregresivo.
\(\theta(B)=1-\theta_1 B-\theta_2 B^2-...-\theta_q B^q\) es el operador de medias móviles.

AR(p)

El modelo AR(p) se puede escribir como: \[(1-\phi_1 B -\phi_2 B^2-...-\phi_p B^p)Z_t=C+a_t,\]

Teorema 1 Considere el polinomio autoregresivo: \[\phi(z)=1-\phi_1 z -\phi_2 z^2-...-\phi_p z^p.\] se puede demostrar que el proceso AR(p) es estacionario si todas las raíces \(z\) del polinomio autoregresivo tienen módulo mayores a 1.¹

Ejemplo: Para un AR(1), la raíz del polinomio autoregresivo es dada por la solución \(z\) que satisface la ecuación \[\begin{align*} \phi(z) &= 1 - \phi_1 z = 0 \Rightarrow\quad 1 = \phi_1 z \\ \Rightarrow\quad z &= \frac{1}{\phi_1} \Rightarrow\quad |z| = \left|\frac{1}{\phi_1}\right| > 1 \\ \Rightarrow\quad 1 &> |\phi_1| \end{align*}\]

Ejemplo: Considere \[Z_t=2+1.5 Z_{t-1}-0.9 Z_{t-2}+a_t\]
La ecuación característica es: \(\phi(B)=1-1.5 B +0.9 B^2\) con raíces imaginarias:

\[B=\frac{1.5\pm \sqrt{2.25-3.6}}{1.8}=\frac{1.5\pm \sqrt{-1.35}}{1.8}=0.83\pm 0.65 i\] donde \(i=\sqrt{-1}\).

Las raíces de la ecuación quedan fuera del círculo unitario ya que \(|B|=\sqrt{0.83^2+0.65^2}=1.05\).

La ecuación característica de un AR(2) es: \(\phi(B)=1-\phi_1 B - \phi_2 B^2\) con raíces imaginarias:

\[z=\frac{\phi_1 \pm \sqrt{\phi_1^2 - 4 \phi_2 (-1)}}{2 (-\phi_2)}.\]

Para que AR(2) sea estacionario, necesitamos que: \[\left|\frac{\phi_1 \pm \sqrt{\phi_1^2 + 4 \phi_2 }}{-2 \phi_2}\right|> 1.\]
Esta condición se puede deducir a las siguientes 3 condiciones: \[|\phi_2|<1\] \[\phi_1+\phi_2<1\] \[-\phi_1+\phi_2<1\].

Estas 3 condiciones: \(|\phi_2|<1\); \(\phi_1+\phi_2<1\); \(-\phi_1+\phi_2<1\), abarcan la siguiente región.

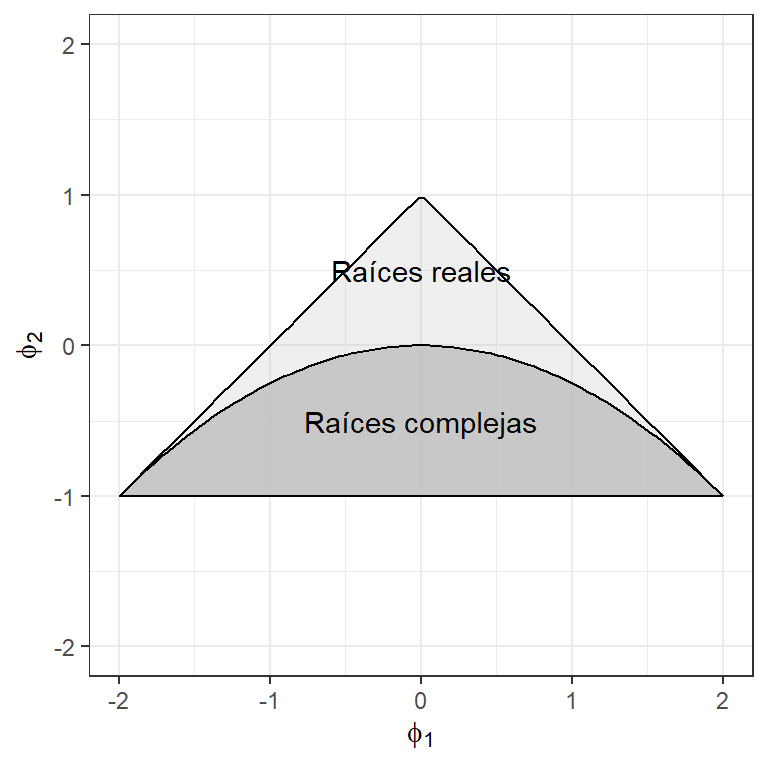
Región de estacionariedad de AR(2)

MA(q)

El modelo MA(q) se puede reescribir como:

\[Z_t-\mu=(1-\theta_1 B-\theta_2 B^2-...-\theta_q B^q)a_t,\]

Teorema 2 Considere el polinomio de medias móviles: \[\theta(z)=1-\theta_1 z-\theta_2 z^2-...-\theta_q z^q\] Se puede demostrar que el proceso MA(q) es invertible si todas las raíces \(z\) del polinomio de medias móviles tienen módulo mayores a 1.¹

Operador de diferencia

Contenido

MA(q)
AR(p)
ARMA(p,q)
Operadores de rezagos
Operador de diferencia
ARIMA(p,d,q)

Operador de diferencia

Recuerde que la primera diferencia de una serie se define como: \[W_t=Z_t-Z_{t-1}.\]
Utilizando la definición del operador de rezagos, \[W_t=Z_t-Z_{t-1}=Z_t-BZ_{t}=(1-B)Z_t.\]
Defina el operador de diferencia \(\nabla\) como \[\nabla Z_t=Z_t-BZ_{t}=(1-B)Z_t\]
De esta forma, se puede generalizar a \(d\) diferencias

\[\nabla^d Z_t=(1-B)^d Z_t\]

Nota

Son diferentes estas dos expresiones

\[(1-B^2)Z_t = Z_t-Z_{t-2},~~\text{y}\] y

\[\nabla^2 Z_t=(1-B)^2 Z_t=(1-2B+B^2)Z_t=Z_t-2Z_{t-1}+Z_{t-2}\]

Compruebe la igualdad anterior con \(\nabla^2 Z_t=\nabla (\nabla Z_t)\) \[\nabla (Z_t-Z_{t-1})=\nabla Z_t- \nabla Z_{t-1}=Z_t-Z_{t-1}-(Z_{t-1}-Z_{t-2})\] \[=Z_t-2 Z_{t-1}+Z_{t-2}\]

ARIMA(p,d,q)

Contenido

MA(q)
AR(p)
ARMA(p,q)
Operadores de rezagos
Operador de diferencia
ARIMA(p,d,q)

ARIMA(p,d,q)

En la práctica, muchas series son no estacionarias pero las diferencias consecutivas de orden \(d\) puede llegar a una serie estacionaria.
Sea \[\tilde{W}_t=\nabla^d \tilde{Z}_t=(1-B)^d \tilde{Z}_t\] la diferencia consecutiva de orden \(d\) de la serie \(\tilde{Z}_t\).
Suponga que después de realizar estas \(d\) diferencias \(\tilde{W}_t\) puede ser representado por un proceso ARMA(p,q), i.e.

\[(1-\phi_1 B -\phi_2 B^2-...-\phi_p B^p)\tilde{W}_t=(1-\theta_1 B-\theta_2 B^2-...-\theta_q B^q)a_t,\] O equivalentemente,

\[(1-\phi_1 B -\phi_2 B^2-...-\phi_p B^p)(1-B)^d \tilde{Z}_t=(1-\theta_1 B-\theta_2 B^2-...-\theta_q B^q)a_t.\]

Usando las notaciones del operador de diferencia, autoregresivo \(\phi(B)\) y de medias móviles \(\theta(B)\),

\[\phi(B)\nabla^d \tilde{Z}_t=\theta(B)a_t.\] donde:
\(\phi(B)=1-\phi_1 B -\phi_2 B^2-...-\phi_p B^p\) es el operador autorregresivo.
\(\theta(B)=1-\theta_1 B-\theta_2 B^2-...-\theta_q B^q\) es el operador de medias móviles.
\(\nabla^d=(1-B)^d\) es el operador de \(d\) diferencias.

Este modelo es denominado modelo autoregresivo integrado de promedios móviles (en inglés: AutoRegressive Integrated Moving Average model).
Se denota con ARIMA(p,d,q).

El término “integrado” proviene del hecho de que cuando \(d=1\), \(Z_t\) se puede presentar como la suma: \[Z_t=W_t+W_{t-1}+W_{t-2}+...,\] i.e. obtener \(Z_t\) sumando (integrando) del proceso estacionario \(W_t\).

\[W_t+W_{t-1}+W_{t-2}+...\] \[=(Z_{t}-Z_{t-1})+(Z_{t-1}-Z_{t-2})+(Z_{t-2}-Z_{t-3})+...\] \[=Z_{t}~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~\]

Condiciones de ARIMA(p,d,q)

La condición de estacionariedad se verifica con la ecuación característica del proceso autoregresivo \[\phi(B)=1-\phi_1 B -\phi_2 B^2-...-\phi_p B^p=0.\]
Si las raíces características de la ecuación característica están fuera del círculo unitario, el proceso AR(p) es estacionario.
De forma similar, la condición de invertibilidad se verifica con la ecuación característica del proceso de medias móviles

\[\theta(B)=1-\theta_1 B-\theta_2 B^2-...-\theta_q B^q=0.\]

Si las raíces características de la ecuación característica están fuera del círculo unitario, el proceso MA(q) es invertible.

Tema 6: Modelos ARIMA de Box&Jenkins⁽²⁾

Paquetes de R

Tabla de resumen 1

MA(q)

MA(q)

AR(p)

AR(p)

ARMA(p,q)

ARMA(p,q)

Operadores de rezagos

Operadores de rezagos

Ejemplo con AR(2)

Ejemplo con MA(2)

ARMA(p,q)

AR(p)

MA(q)

Operador de diferencia

Operador de diferencia

ARIMA(p,d,q)

ARIMA(p,d,q)

Condiciones de ARIMA(p,d,q)

Próximo tema

Modelos ARIMA de Box&Jenkins - Parte 3

Identificación, estimación y diagnóstico de modelos ARIMA.

Tema 6: Modelos ARIMA de Box&Jenkins(2)

Paquetes de R

Tabla de resumen 1

MA(q)

MA(q)

AR(p)

AR(p)

ARMA(p,q)

ARMA(p,q)

Operadores de rezagos

Operadores de rezagos

Ejemplo con AR(2)

Ejemplo con MA(2)

ARMA(p,q)

AR(p)

MA(q)

Operador de diferencia

Operador de diferencia

ARIMA(p,d,q)

ARIMA(p,d,q)

Condiciones de ARIMA(p,d,q)

Próximo tema

Modelos ARIMA de Box&Jenkins - Parte 3

Identificación, estimación y diagnóstico de modelos ARIMA.

Tema 6: Modelos ARIMA de Box&Jenkins⁽²⁾