Tema 7: Modelos de regresión dinámica
Paquetes de R
Para este tema, se necesita cargar estos paquetes:
Introducción
Contenido
Introducción
Regresión lineal con error de tipo ARIMA
Serie estacionaria por tendencia y por diferencia.
Regresión con covariables rezagadas
Análisis de intervención
Introducción
- En el Tema 4, hemos visto regresión con series de tiempo:
\[Y_t=\beta_0+\beta_1 X_{t,1}+\beta_2 X_{t,2}+...+\beta_p X_{t,p}+\epsilon_t, ~~t=1,...,T,\] en donde \(\left\lbrace \epsilon_t \right\rbrace\) es ruido blanco Gaussiano.
Los modelos de regresión dinámicos son modelos de regresión en los que el término de error sigue un modelo ARIMA.
Veremos que una forma es considerar la variable independiente \(X_t\) influye a \(Y_t\) no solo instantáneamente en el tiempo \(t\) sino a través de varios periodos.
El caso con únicamente una covariable es dado por: \[Y_t=\beta_0+\beta_1 X_{t}+\beta_2 X_{t-1}+...+\beta_p X_{t-p}+\eta_t\] \[\left\lbrace \eta_t \right\rbrace \sim ARIMA(p,d,q)\]
Regresión lineal con error de tipo ARIMA
Contenido
Introducción
Regresión lineal con error de tipo ARIMA
Serie estacionaria por tendencia y por diferencia.
Regresión con covariables rezagadas
Análisis de intervención
Regresión lineal con error de tipo ARIMA
- Primeramente, considere el siguiente modelo: \[Y_t=\beta_0+\beta_1 X_{t,1}+\beta_2 X_{t,2}+...+\beta_p X_{t,p}+\eta_t, ~~t=1,...,T,\] en donde \(\left\lbrace \eta_t \right\rbrace \sim ARIMA(p,d,q)\), i.e.
\[\phi(B) (1-B)^d \eta_t=\theta(B) \epsilon_t,\] con ruido blanco \(\left\lbrace \epsilon_t \right\rbrace\).
- La estimación de los parámetros del modelo minimizando la suma de cuadrados \(\eta_t\) en vez de \(\eta_t\) ignorando su estructura dependiente del tiempo es incorrecta.
- La estimación de los coeficientes \(\beta_i, i=1,...,p\) no satisfacen las propiedades óptimas (insesgamiento, variancia mínima, etc.). Por lo tanto, toda la teoría de inferencia, pruebas de hipótesis de regresión no funciona.
Nota
- Verifique que la variable \(Y_t\) y las \(X_{t1},X_{t2},...,X_{tp}\) sean estacionarias, porque si se estiman los coeficientes con variables no estacionarias, los estimadores no son consistentes.
- Además, podría presentar problema de la regresión espuria.
- Realice diferencias a las variables no estacionarias.
- El modelo después de aplicar la diferencia es llamado modelo de regresión en diferencias.
- Se puede demostrar que el modelo de regresión con error de tipo ARIMA es equivalente a un modelo de regresión en diferencias con error tipo ARMA.
- Por ejemplo, considere \[Y_t=\beta_0+\beta_1 X_{t,1}+\beta_2 X_{t,2}+...+\beta_p X_{t,p}+\eta_t, ~~t=1,...,T,\] \[(1-\phi_1B) (1-B) \eta_t=(1-\theta_1 B) \epsilon_t,\]
- Después de aplicar las diferencias \[Y'_t=Y_{t}-Y_{t-1}, ~~~~ X'_{t,k}=X_{t,k}-X_{t-1,k},~k=1,...,p,~~\text{y}~~ \eta'_t=\eta_t-\eta_{t-1}\]
obtenemos
\[Y'_t=\beta_1 X'_{t,1}+\beta_2 X'_{t,2}+...+\beta_p X'_{t,p}+\eta'_t, ~~t=1,...,T,\] \[(1-\phi_1B) \eta'_t=(1-\theta_1 B) \epsilon_t,\]
- En
R, si queremos ajustar un modelo de regresión con error tipo ARIMA(1,1,0), i.e. \[Y_t=\beta_0+\beta_1 X_{t,1}+\eta_t\] \[(1-\phi_1B) (1-B) \eta_t=\epsilon_t,\] con el siguiente comando:
- El programa considera el modelo en diferencias con error tipo AR(1):
\[Y'_t=\beta_1 X'_{t1}+\eta_t\] \[(1-\phi_1B) \eta_t=\epsilon_t,\]
- Ejemplo tomado de Hyndman (2018): pronóstico del cambio de gasto basado en el ingreso personal (serie trimestral) de 01-1970 a 03-2016.
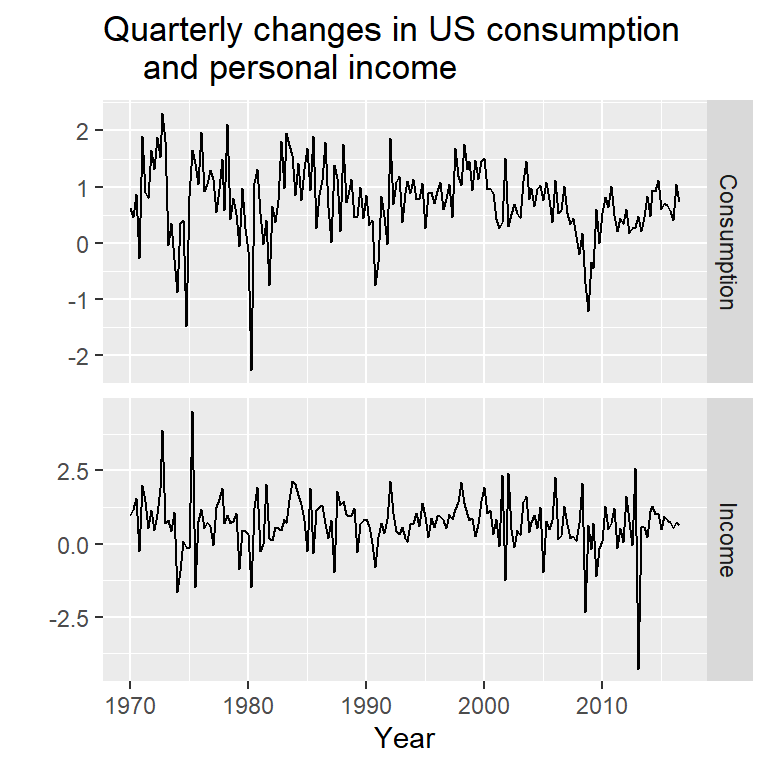
Como ilustración, note que son equivalentes:
y <- uschange[,"Consumption"]
x <- uschange[,"Income"]
mod0 <- Arima(y, xreg=x, order=c(1,1,0))
summary(mod0)Series: y
Regression with ARIMA(1,1,0) errors
Coefficients:
ar1 xreg
-0.5412 0.1835
s.e. 0.0638 0.0429
sigma^2 = 0.3982: log likelihood = -177.46
AIC=360.93 AICc=361.06 BIC=370.61
Training set error measures:
ME RMSE MAE MPE MAPE MASE
Training set 0.002476011 0.6259787 0.4671324 21.24398 182.2579 0.7319011
ACF1
Training set -0.1727835Series: diff(y)
Regression with ARIMA(1,0,0) errors
Coefficients:
ar1 intercept xreg
-0.5413 0.0019 0.1835
s.e. 0.0638 0.0299 0.0429
sigma^2 = 0.4004: log likelihood = -177.46
AIC=362.93 AICc=363.15 BIC=375.83
Training set error measures:
ME RMSE MAE MPE MAPE MASE
Training set -0.0003963677 0.6276524 0.4697909 -181.0816 364.3807 0.5583989
ACF1
Training set -0.1727715Series: y
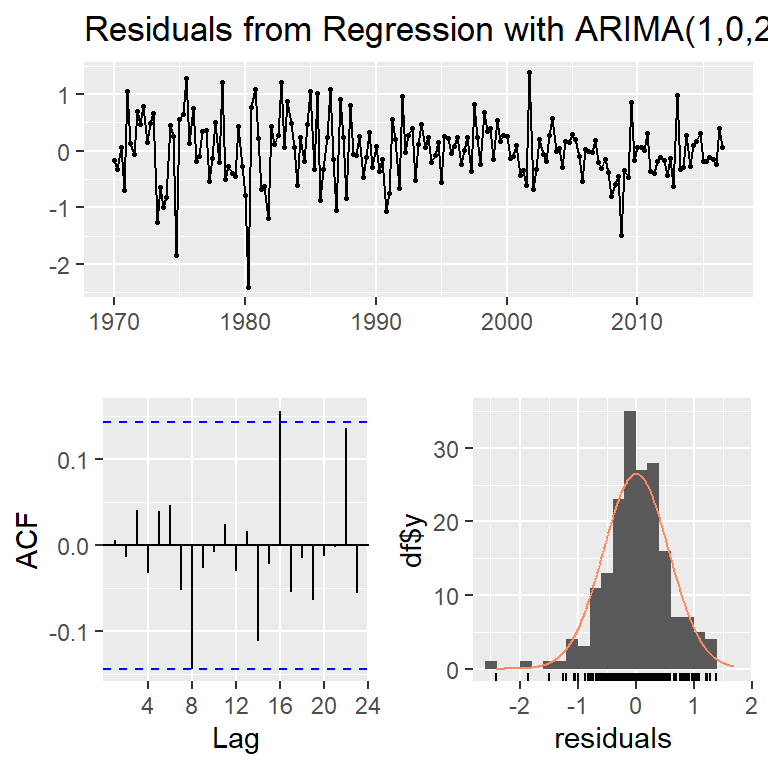
Regression with ARIMA(1,0,2) errors
Coefficients:
ar1 ma1 ma2 intercept xreg
0.6922 -0.5758 0.1984 0.5990 0.2028
s.e. 0.1159 0.1301 0.0756 0.0884 0.0461
sigma^2 = 0.3219: log likelihood = -156.95
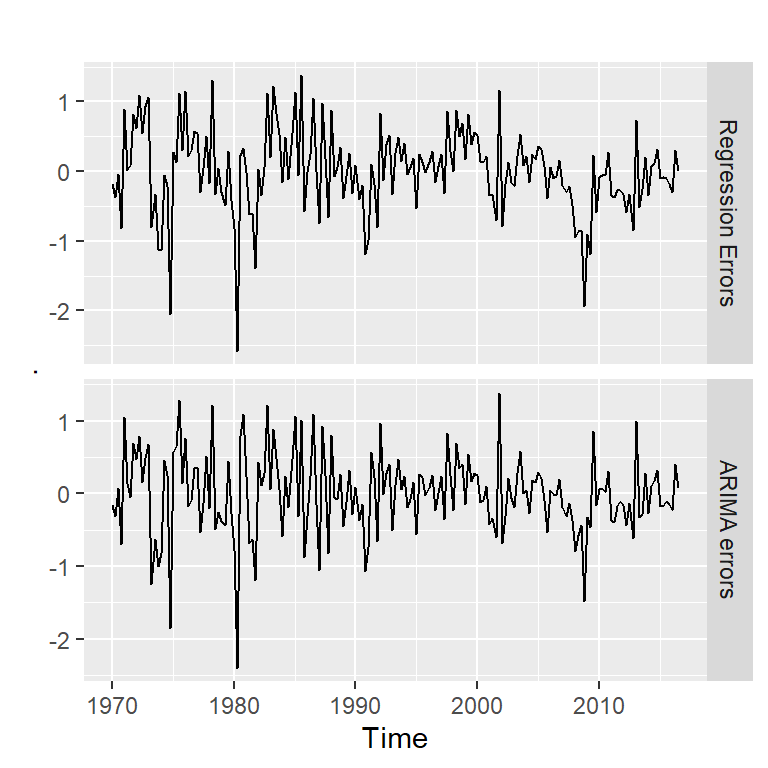
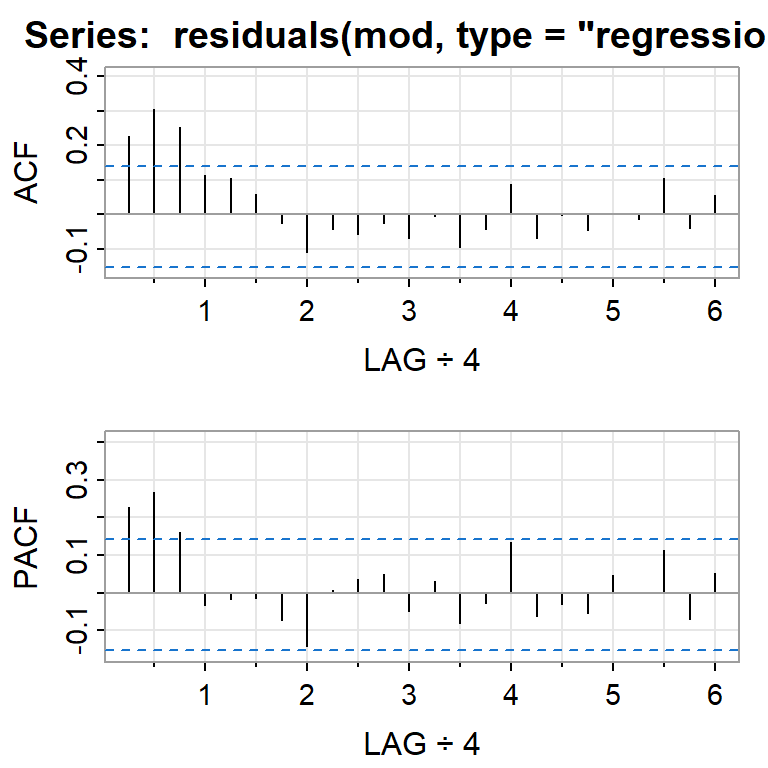
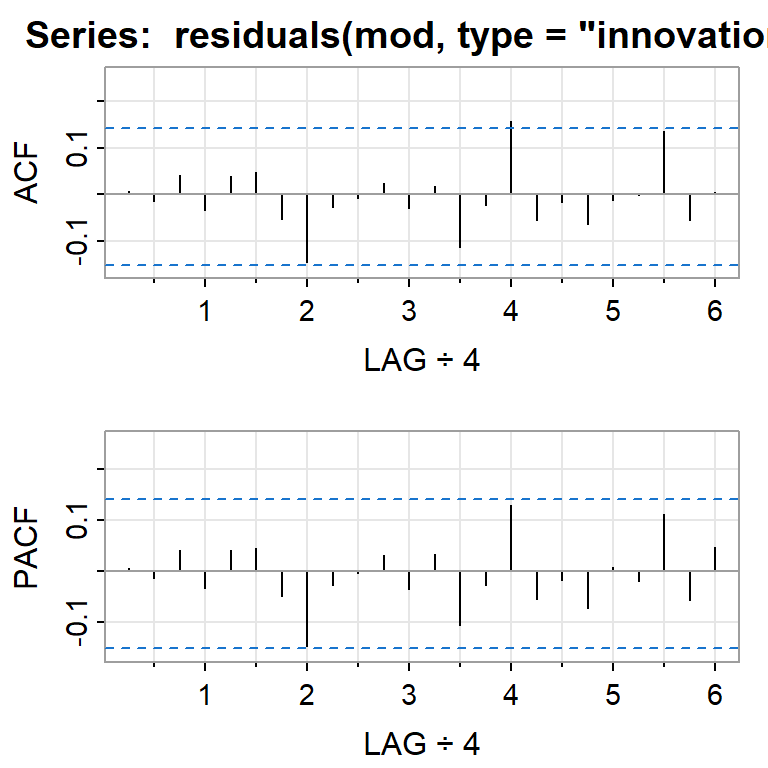
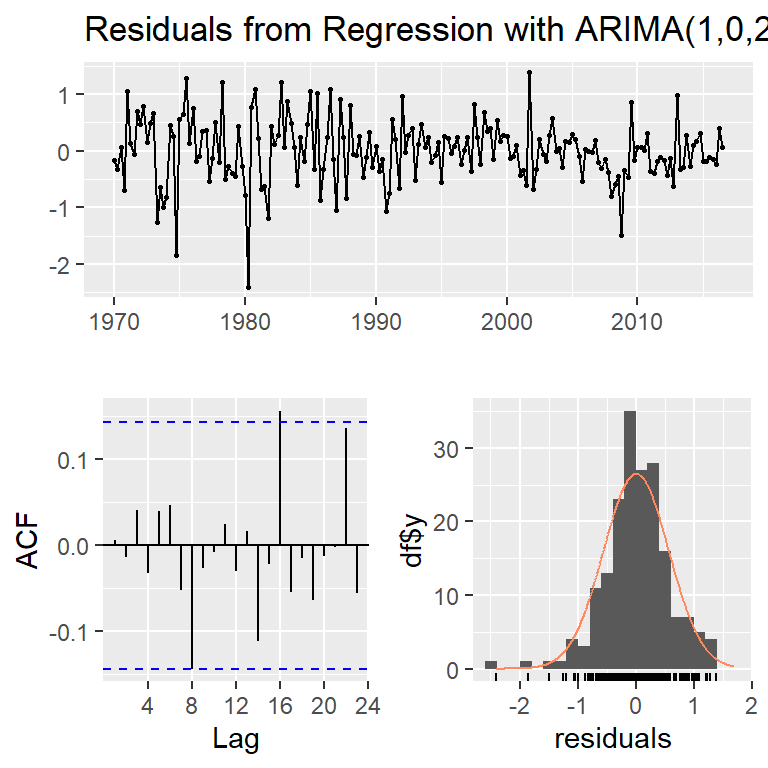
AIC=325.91 AICc=326.37 BIC=345.29El modelo final estimado es:
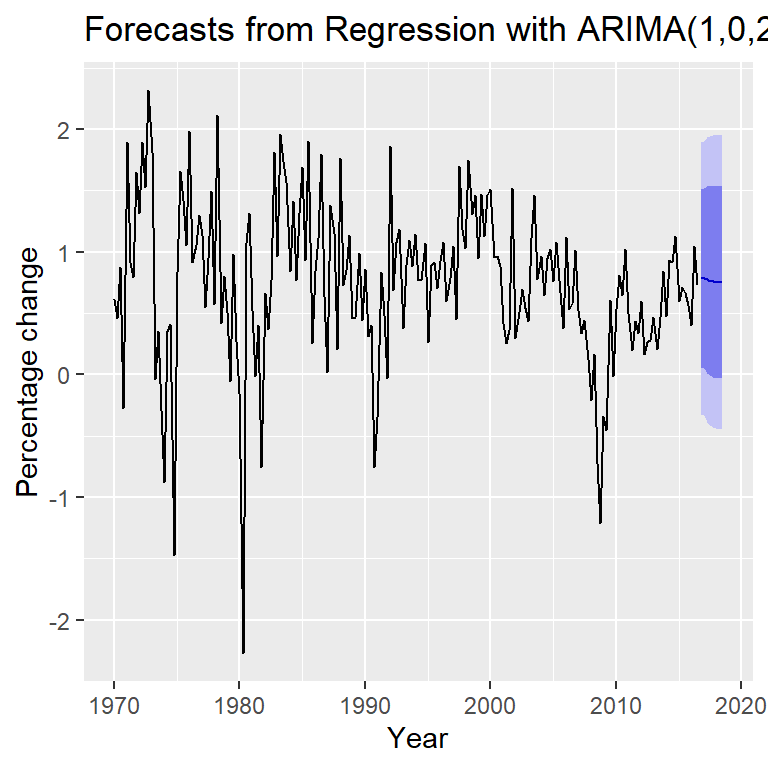
\[Y_t=0.599+ 0.203 X_{t1}+\eta_t\] \[\eta_t=0.692 \eta_{t-1}+\epsilon_t-0.576 \epsilon_{t-1}+ 0.198\epsilon_{t-2},\] \[\epsilon_{t} \sim N(0,0.322)\]
Pronóstico
Serie estacionaria por tendencia y por diferencia.
Contenido
Introducción
Regresión lineal con error de tipo ARIMA
Serie estacionaria por tendencia y por diferencia.
Regresión con covariables rezagadas
Análisis de intervención
Serie estacionaria por tendencia y por diferencia.
Suponga que una serie temporal \(\left\lbrace Y_t \right\rbrace\) es una realización de una tendencia determinística y un componente estocástico:
\[ Y_t=TD_t+ \eta_t, \] donde \(TD_t=\beta_0+\beta_1 t\) y \(\eta_t \sim ARIMA(p,d,q)\).
Caso 1: si \(d=0\), \(\left\lbrace Y_t \right\rbrace\) es estacionaria alrededor de una tendencia determinística. Por lo tanto, se puede eliminar la tendencia de la serie original y ajustar un modelo ARMA a los residuales.
Caso 2: si \(d>0\), \(\left\lbrace Y_t \right\rbrace\) es estacionaria por diferencia. Por lo tanto, se puede realizar una diferencia para obtener una serie estacionaria. Caso más común es cuando \(d=1\).
Ejemplo de estos dos tipos de estacionariedad:
- Tendencia determinística: \[Y_t=Y_{t-1}+\mu=Y_0+\mu t\]
- Tendencia estocástica (acumulación de choques aleatorias): \[Y_t=Y_{t-1}+\epsilon_t=Y_0+\sum_{s=1}^t \epsilon_s\] donde \(\mu\) es una constante y \(\epsilon_t\) es ruido blanco.
- En síntesis, una serie temporal \(\left\lbrace Y_t \right\rbrace\) está compuesto por una tendencia determinística y un componente estocástico que es modelado por \(ARIMA(p,d,q)\).
- Se puede descomponer \(\eta_t\) en dos componentes: tendencia estocástica (choques aleatorios) y el componente aleatorio “estacionario”.
- Entonces, \(\left\lbrace Y_t \right\rbrace\) se puede descomponer en tres componentes:
- tendencia determinística,
- tendencia estocástica, y
- el componente “aleatorio”.
- Un modelo estacionario por tendencia, no tiene la tendencia estocástica, y el componente aleatorio es \(ARMA(p,q)\).
- En el caso de un modelo estacionario por diferencia, el polinomio autoregresivo del componente \(\eta_t\) tiene al menos una raíz unitaria.
Ejemplo simulado
Tendencia determinística: \(Y_t= 0 + 0.5 t + \epsilon_t\)
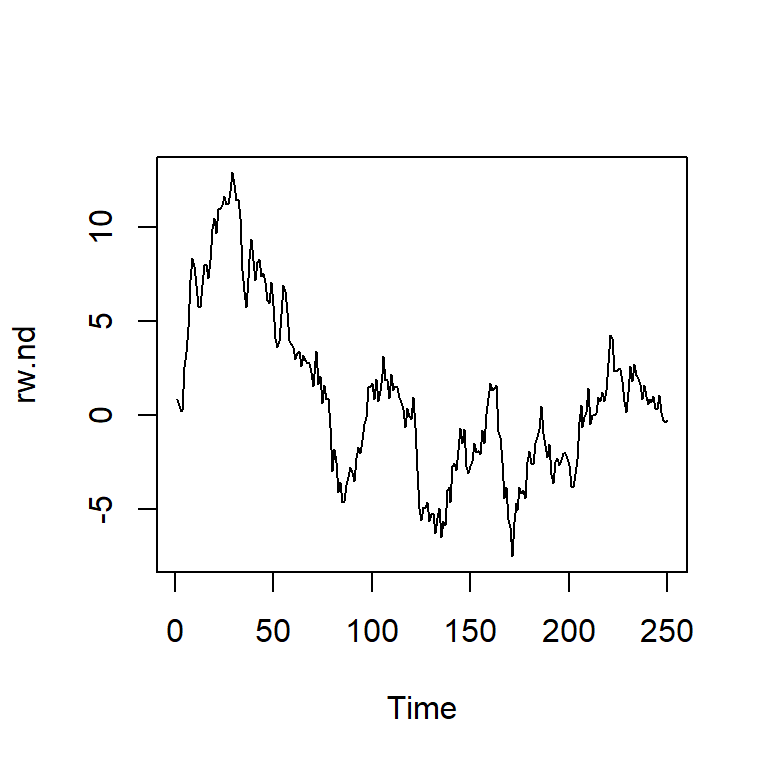
Tendencia estocástica: \(Y_t = \sum_{s=1}^t \epsilon_s\)
- Tendencia determinística con tendencia estocástica: \(Y_t= 0 + 0.5 t + \sum_{s=1}^t \epsilon_s\)
tend <- 1:250 ## tendencia
dt <- e + 0.5*tend ## tendencia determinística con ruido
rw.wd <- 0.5*tend + cumsum(e) ## caminata aleatoria con desvío
plot.ts(dt, lty=1, col=1)
lines(rw.wd, lty=2, col= 2)
legend("topleft", legend=c('tend. det. + ruido',
'tend. det. + tend. est.'),
lty=c(1, 2),col=c(1,2)) 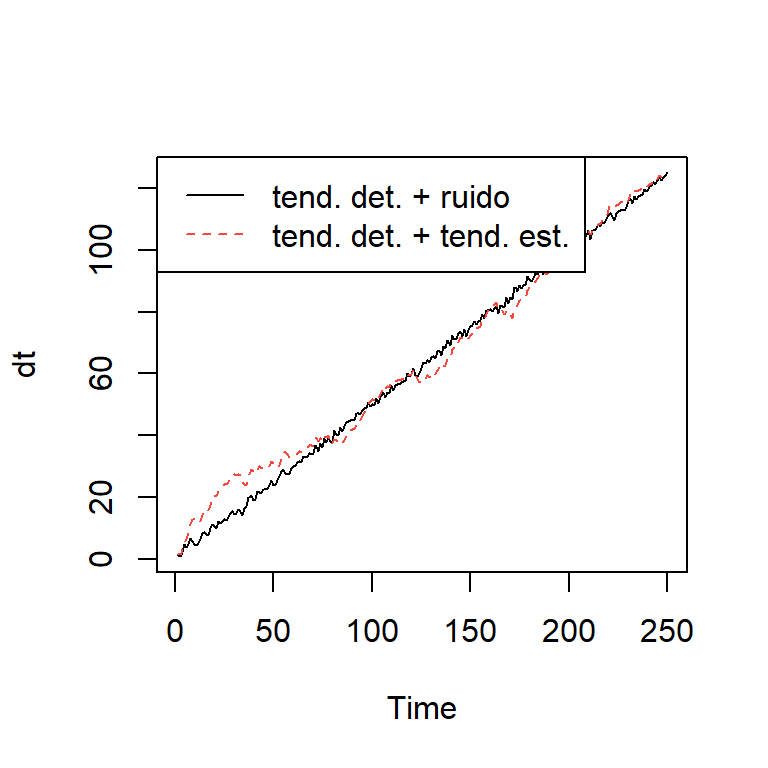
Tendencia determinística y estocástica
- Devolviendo al modelo regresión, en la práctica se puede modelar una tendencia lineal usando: \[Y_t=\beta_0+\beta_1 t + \eta_t\]
- \(\eta_t \sim ARMA(p,q)\), o
- \(\eta_t \sim ARIMA(p,1,q)\).
- En el caso 2, se puede simplificar el modelo en: \[Y_t=Y_{t-1}+\beta_1+ \eta'_t.\] Este modelo es similar a un modelo de caminata aleatoria pero con un desvío \(\beta_1\) y el error es ARMA.
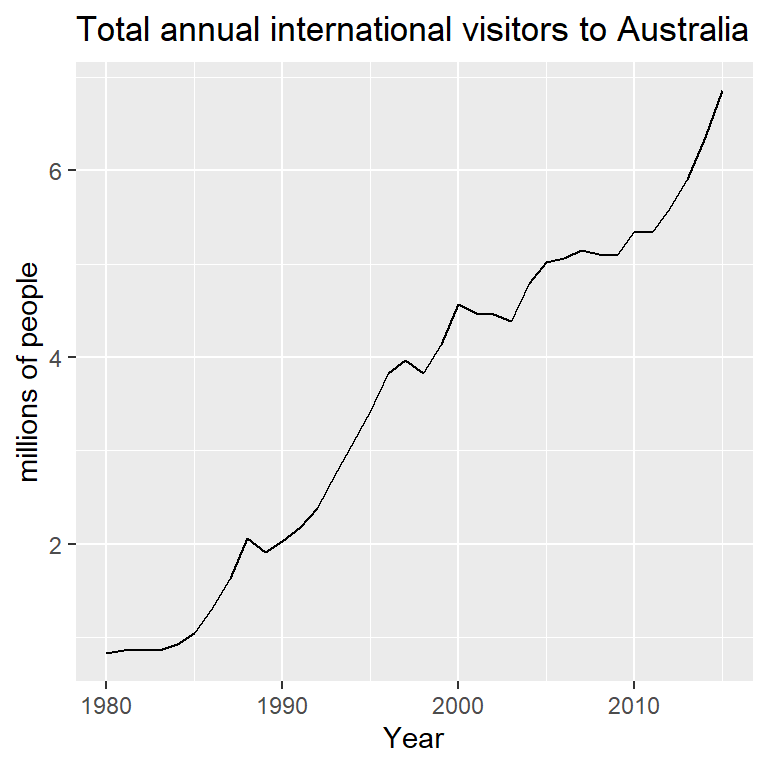
Ajuste con tendencia determinística
Series: austa
Regression with ARIMA(2,0,0) errors
Coefficients:
ar1 ar2 intercept xreg
1.1127 -0.3805 0.4156 0.1710
s.e. 0.1600 0.1585 0.1897 0.0088
sigma^2 = 0.02979: log likelihood = 13.6
AIC=-17.2 AICc=-15.2 BIC=-9.28\[Y_t=0.416+0.171t+\eta_t\] \[\eta_t=1.113\eta_{t-1}-0.380 \eta_{t-2}+\epsilon_t\] \[\epsilon_t \overset{iid}{\sim} N(0,0.03)\]
Ajuste con tendencia estocástica
Series: austa
ARIMA(0,1,1) with drift
Coefficients:
ma1 drift
0.3006 0.1735
s.e. 0.1647 0.0390
sigma^2 = 0.03376: log likelihood = 10.62
AIC=-15.24 AICc=-14.46 BIC=-10.57\[Y_t-Y_{t-1}=0.173+\eta'_t,\] o de otra forma,
\[Y_t=Y_0+0.173t+\eta_t\] \[\eta_t=\eta_{t-1}+0.301\epsilon_{t-1}+\epsilon_t\] \[\epsilon_t \overset{iid}{\sim} N(0,0.034)\]
fc1 <- forecast(fit1,
xreg = length(austa) + 1:10)
fc2 <- forecast(fit2, h=10)
autoplot(austa) +
autolayer(fc2, series="Stochastic trend") +
autolayer(fc1, series="Deterministic trend") +
ggtitle("Forecasts from trend models") +
xlab("Year") + ylab("Visitors to Australia (millions)") +
guides(colour=guide_legend(title="Forecast"))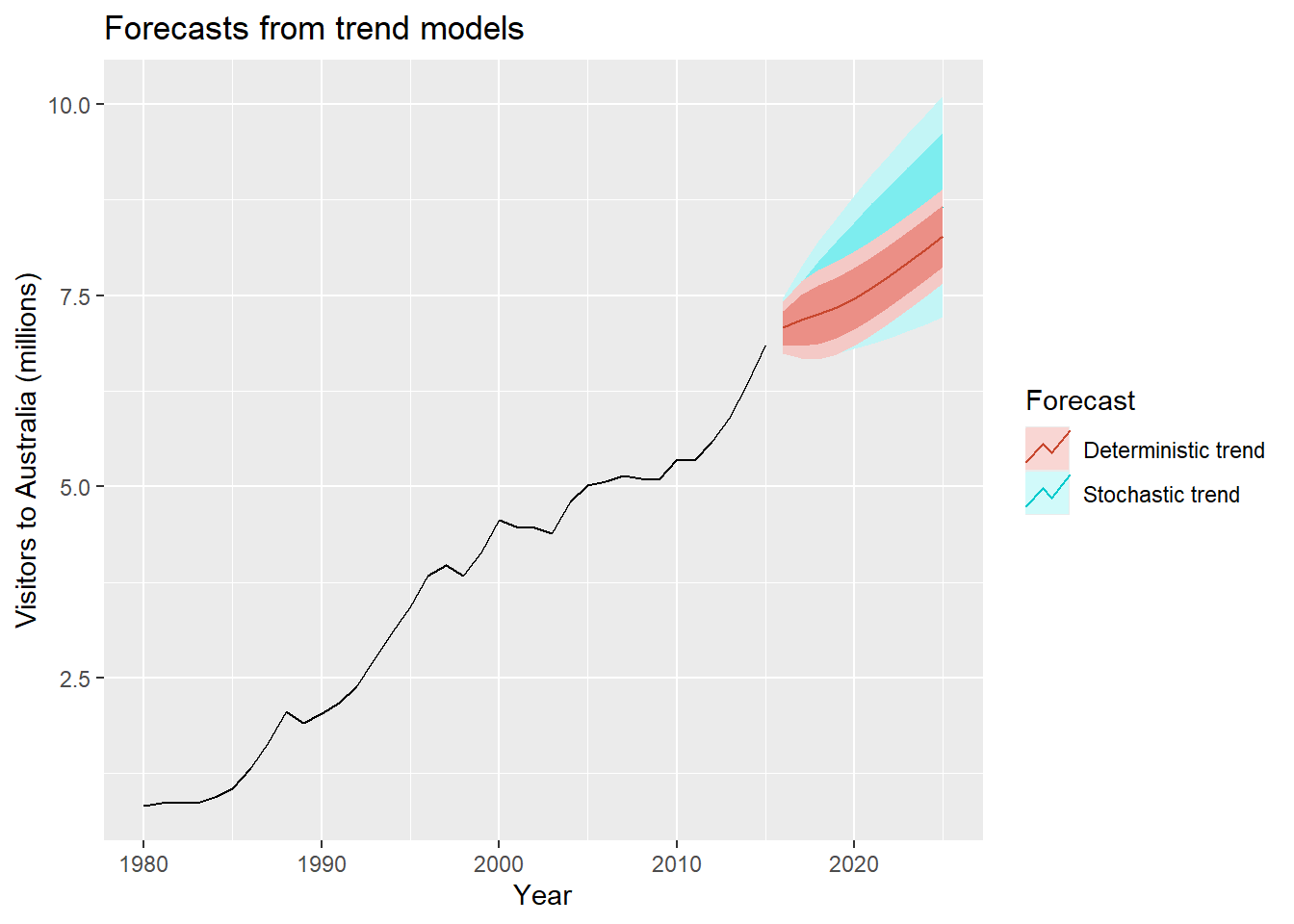
Regresión con covariables rezagadas
Contenido
Introducción
Regresión lineal con error de tipo ARIMA
Serie estacionaria por tendencia y por diferencia.
Regresión con covariables rezagadas
Análisis de intervención
Regresión con covariables rezagadas
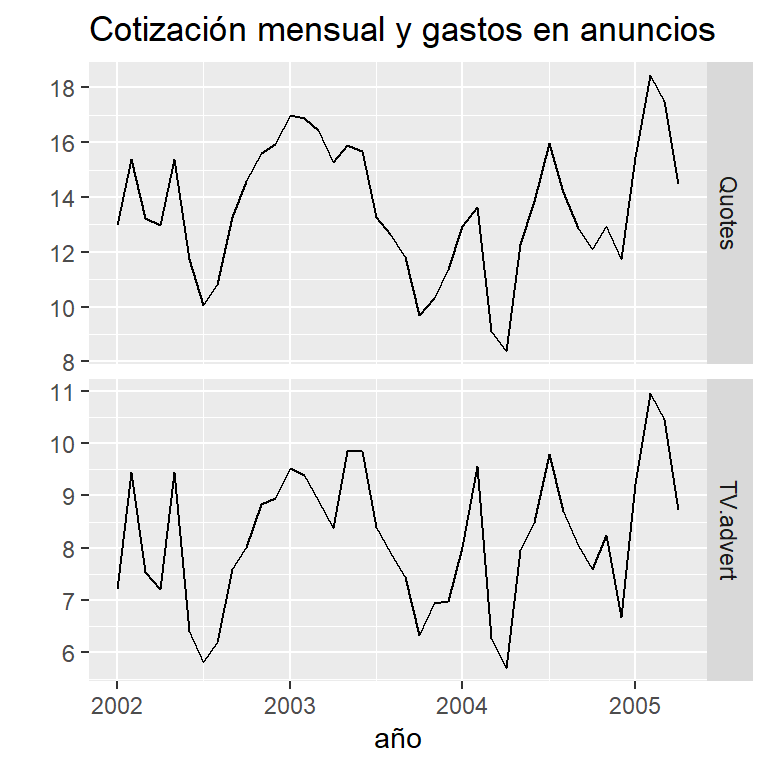
- Cotización mensual y gastos en publicidad de una compañía estadounidense (enero 2002- abril 2005)
- Predictores rezagadas (0,1,2 y 3 rezagos)
anuncios <- cbind(
x0 = x,
x1 = stats::lag(x,-1),
x2 = stats::lag(x,-2),
x3 = stats::lag(x,-3)) %>%
head(NROW(insurance)) #eliminar los NA al final
anuncios[1:10,] x0 x1 x2 x3
[1,] 7.212725 NA NA NA
[2,] 9.443570 7.212725 NA NA
[3,] 7.534250 9.443570 7.212725 NA
[4,] 7.212725 7.534250 9.443570 7.212725
[5,] 9.443570 7.212725 7.534250 9.443570
[6,] 6.415215 9.443570 7.212725 7.534250
[7,] 5.806990 6.415215 9.443570 7.212725
[8,] 6.203600 5.806990 6.415215 9.443570
[9,] 7.586430 6.203600 5.806990 6.415215
[10,] 8.004935 7.586430 6.203600 5.806990Ajuste de modelos
Series: insurance[4:40, 1]
Regression with ARIMA(2,0,0) errors
Coefficients:
ar1 ar2 intercept xreg
1.2321 -0.4642 3.4263 1.2413
s.e. 0.1636 0.1708 0.6805 0.0751
sigma^2 = 0.2891: log likelihood = -28.28
AIC=66.56 AICc=68.5 BIC=74.62Series: insurance[4:40, 1]
Regression with ARIMA(1,0,1) errors
Coefficients:
ar1 ma1 x0 x1
0.6718 0.6713 1.3770 0.2745
s.e. 0.1324 0.1302 0.0374 0.0362
sigma^2 = 0.2285: log likelihood = -24.04
AIC=58.09 AICc=60.02 BIC=66.14Series: insurance[4:40, 1]
Regression with ARIMA(1,0,1) errors
Coefficients:
ar1 ma1 x0 x1 x2
0.6701 0.6757 1.3843 0.2764 -0.0111
s.e. 0.1349 0.1311 0.0487 0.0369 0.0470
sigma^2 = 0.2352: log likelihood = -24.02
AIC=60.03 AICc=62.83 BIC=69.7Series: insurance[4:40, 1]
Regression with ARIMA(1,0,1) errors
Coefficients:
ar1 ma1 intercept x0 x1 x2 x3
0.7567 0.6071 3.6314 1.2901 0.1323 -0.1303 -0.0643
s.e. 0.1155 0.1369 1.8656 0.0656 0.0797 0.0759 0.0612
sigma^2 = 0.2262: log likelihood = -22.16
AIC=60.31 AICc=65.46 BIC=73.2[1] 68.49968 60.02357 62.83253 65.45747Series: insurance[, 1]
Regression with ARIMA(3,0,0) errors
Coefficients:
ar1 ar2 ar3 intercept x0 x1
1.4117 -0.9317 0.3591 2.0393 1.2564 0.1625
s.e. 0.1698 0.2545 0.1592 0.9931 0.0667 0.0591
sigma^2 = 0.2165: log likelihood = -23.89
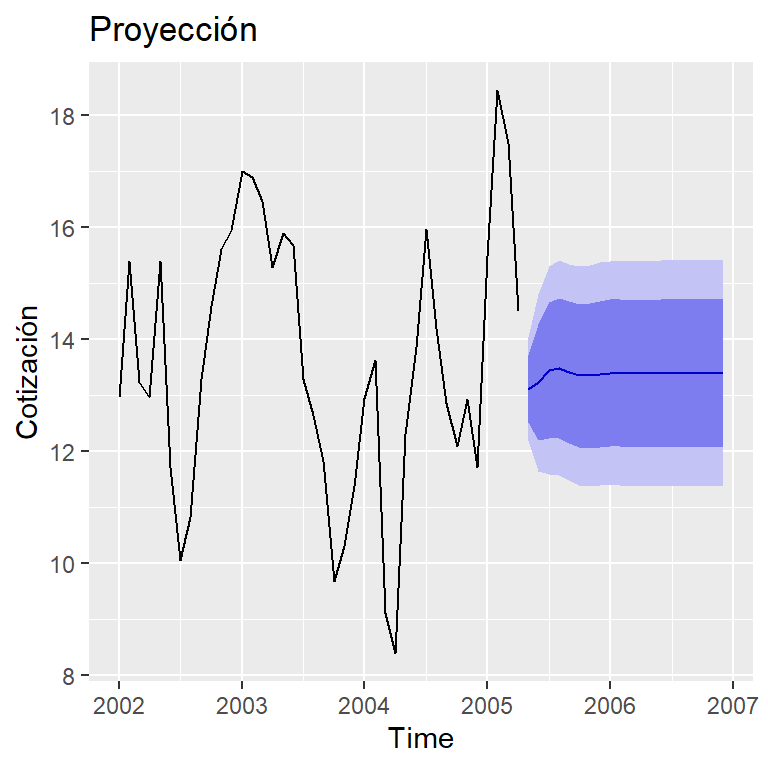
AIC=61.78 AICc=65.4 BIC=73.43pronóstico
Análisis de intervención
Contenido
Introducción
Regresión lineal con error de tipo ARIMA
Serie estacionaria por tendencia y por diferencia.
Regresión con covariables rezagadas
Análisis de intervención
Análisis de intervención
Una serie puede experimentar cambios de comportamiento en el tiempo cuando ocurren fenómenos como cambios en las políticas públicas, desastres naturales, crisis económicas serias, aumentos sustanciales en gastos de publicidad, etc.
La suposición del mismo comportamiento a lo largo de tiempo puede ser no realista.
El análisis de intervención introducida por Box & Tiao en 1975 toma en cuenta este tipo de eventos.
Ilustramos el análisis con el siguiente ejemplo (Wichern & Jones, 1977).
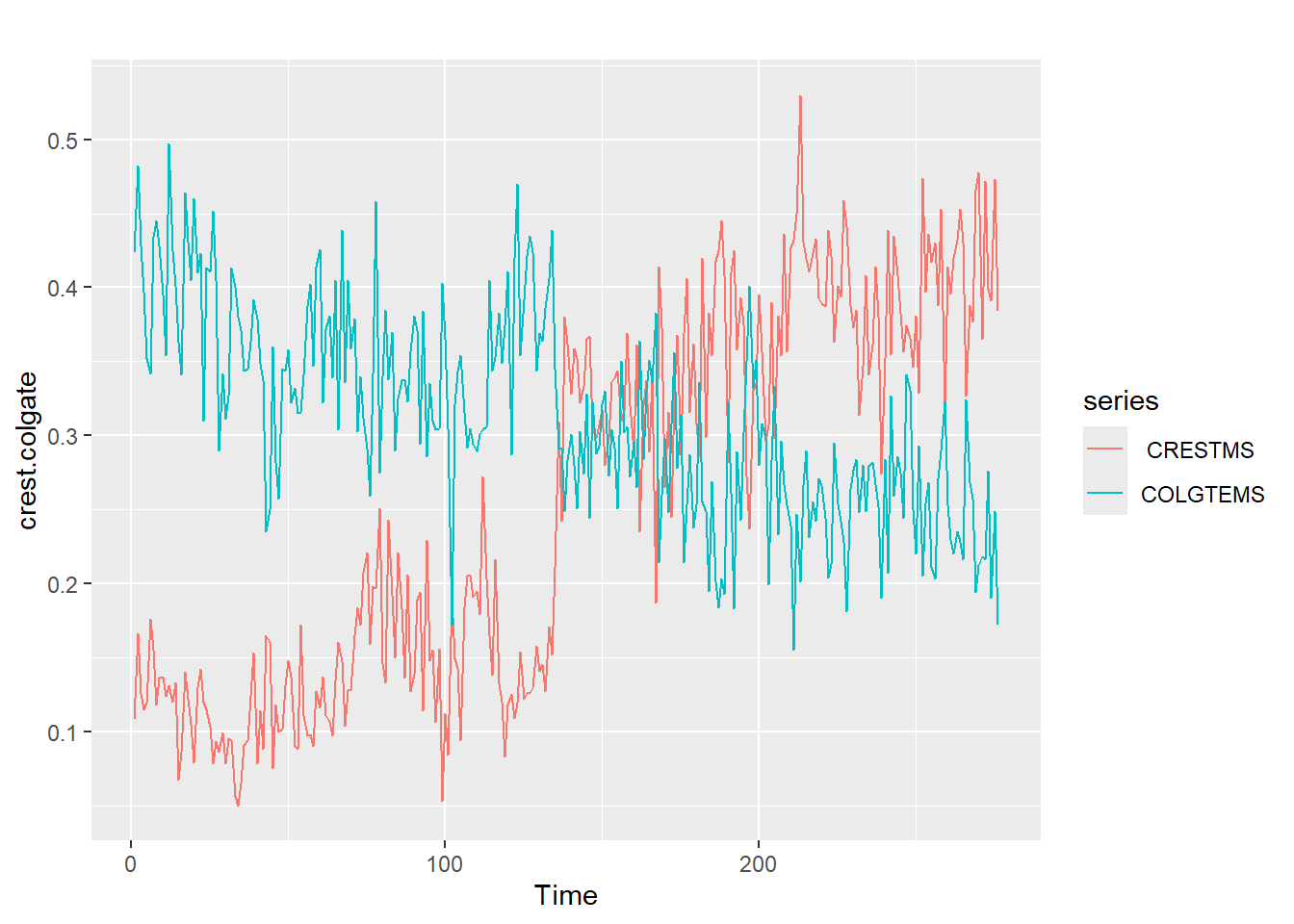
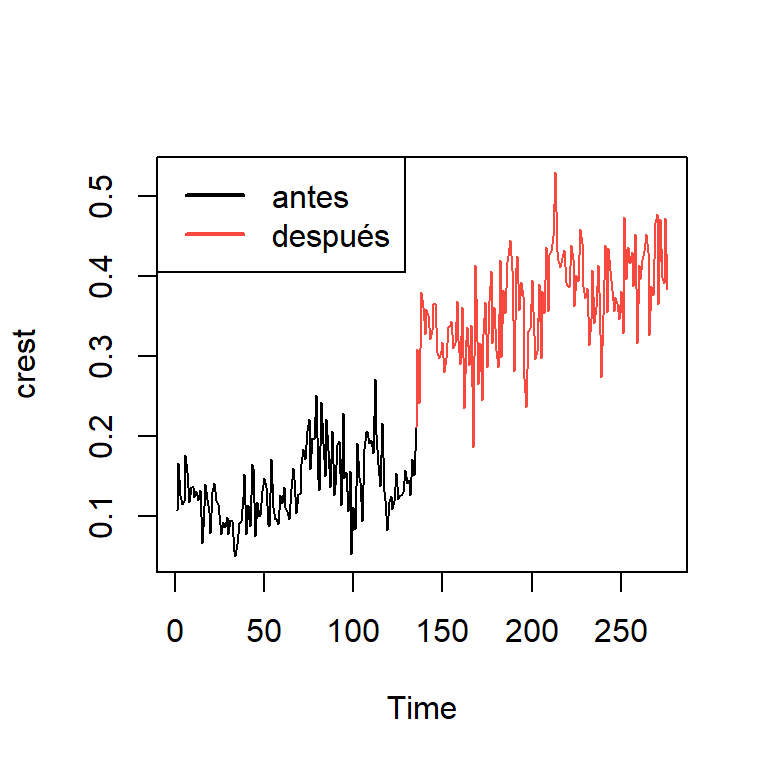
Ejemplo de Crest
- Series semanales de cuotas de mercado dentífrico de las marcas Colgate y Crest en los Estados Unidos de 1 de enero de 1958 al abril de 1963.
- Al inicio, Colgate aventajaba a la marca Crest en el mercado.
- El 1 de agosto de 1960 ocurrió el cambio de comportamiento: la Asociación Dental Americana dio un respaldo enorme a la marca Crest al hacer público que era una pasta dental eficaz para prevenir las caries dentales.
- Procter y Gamble, la compañía que producía la marca Crest, aprovechó y divulgó intensamente durante dos semanas el enuncio.
Pasos del análisis de intervención
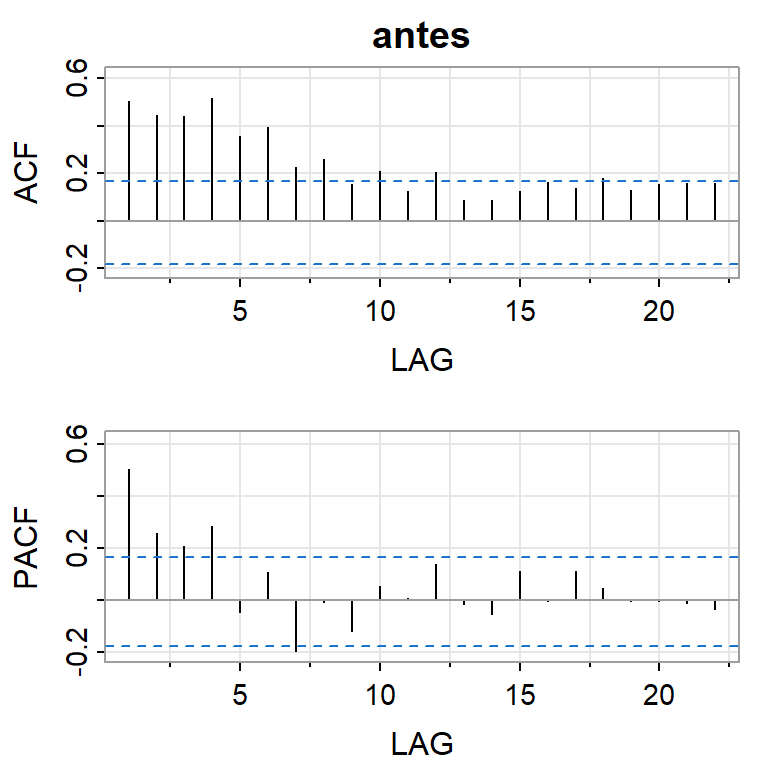
- Asumimos que antes de la intervención, la serie se puede modelar con ARIMA.
Elaborar un modelo ARIMA antes de la intervención, i.e. durante las primeras 134 semanas.
Ampliar el modelo agregando variables indicadoras para registrar la intervención.
Reestimar el modelo con la serie completa con las variables indicadoras.
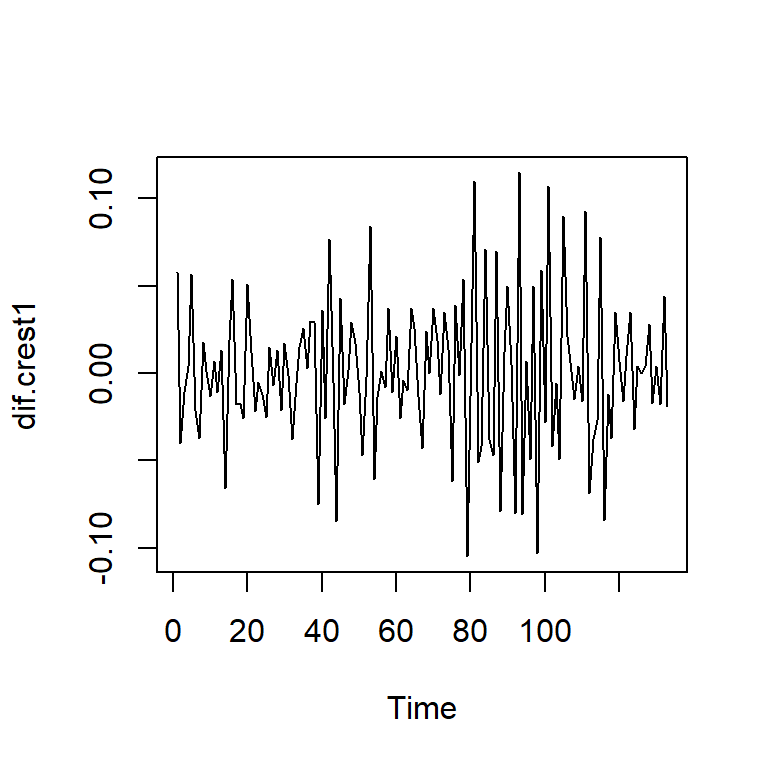
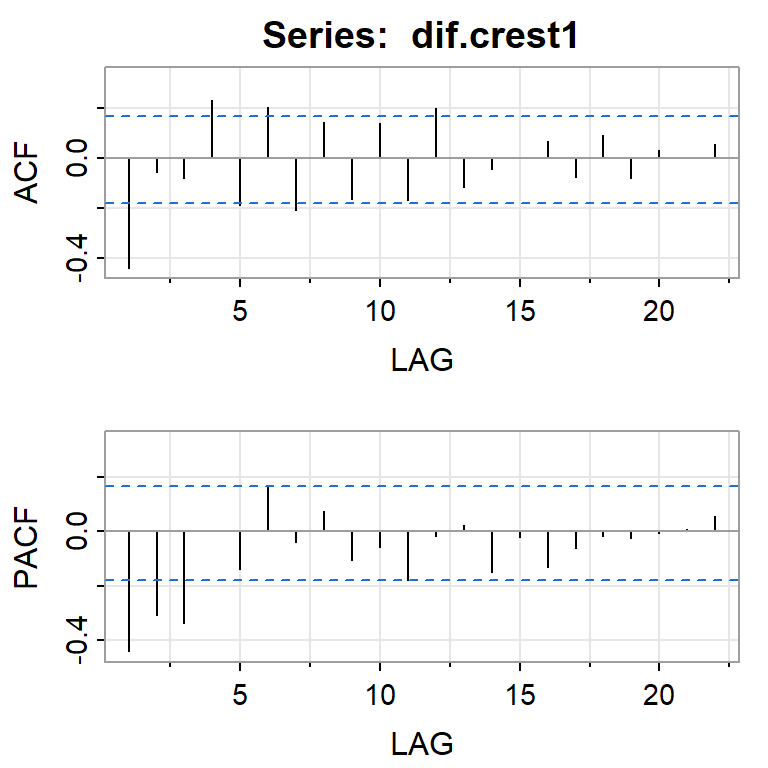
- Serie diferenciada (antes de la intervención)
- Vamos a ajustar un ARIMA(0,1,1): \[(1-B)Z_t=(1-\theta_1B)a_t\]
Series: crest1
ARIMA(0,1,1)
Coefficients:
ma1
-0.6918
s.e. 0.0644
sigma^2 = 0.001248: log likelihood = 256.11
AIC=-508.22 AICc=-508.12 BIC=-502.44
Training set error measures:
ME RMSE MAE MPE MAPE MASE
Training set 0.0006404213 0.03505771 0.02747198 -5.725771 22.02557 0.8434379
ACF1
Training set -0.0009184472El modelo se puede despejar \(Z_t\): \[Z_t=\frac{(1-\theta_1B)}{(1-B)}a_t\]
Creación de variables indicadoras para indicar la intervención: \[I_{1t}=\left\lbrace \begin{aligned} 0, & & \text{si}~~ t<135 \\ 1, & & \text{si}~~ t \geq135, \end{aligned} \right., ~~ \text{y}~~~I_{2t}=\left\lbrace \begin{aligned} 0, & & \text{si}~~ t<136 \\ 1, & & \text{si}~~ t \geq136, \end{aligned} \right.\]
El modelo ARIMA con intervención: \[Z_t=c_1 I_{1t} +c_2 I_{2t}+ \frac{(1-\theta_1B)}{(1-B)}a_t.\]
Multiplicando por ambos lados \((1-B)\): \[(1-B) Z_t=c_1 (1-B) I_{1t} +c_2 (1-B) I_{2t}+ (1-\theta_1B)a_t\] Note que en realidad, estamos modelando la intervención como un impulso en la serie diferenciada.
Series: crest
Regression with ARIMA(0,1,1) errors
Coefficients:
ma1 I1 I2
-0.7782 0.0654 0.1119
s.e. 0.0437 0.0434 0.0434
sigma^2 = 0.001902: log likelihood = 472.22
AIC=-936.44 AICc=-936.29 BIC=-921.98
Training set error measures:
ME RMSE MAE MPE MAPE MASE
Training set 0.00186971 0.04329952 0.03363337 -3.49533 16.66087 0.7903928
ACF1
Training set -0.01155037- La intervención produce el cambio a partir de la segunda semana.
Series: crest
Regression with ARIMA(0,1,1) errors
Coefficients:
ma1 I2
-0.7758 0.1624
s.e. 0.0442 0.0283
sigma^2 = 0.001911: log likelihood = 471.09
AIC=-936.18 AICc=-936.09 BIC=-925.33
Training set error measures:
ME RMSE MAE MPE MAPE MASE
Training set 0.002091025 0.04347852 0.03386705 -3.380261 16.76654 0.7958844
ACF1
Training set -0.01500684
Ljung-Box test
data: Residuals from Regression with ARIMA(0,1,1) errors
Q* = 16.273, df = 19, p-value = 0.639
Model df: 1. Total lags used: 20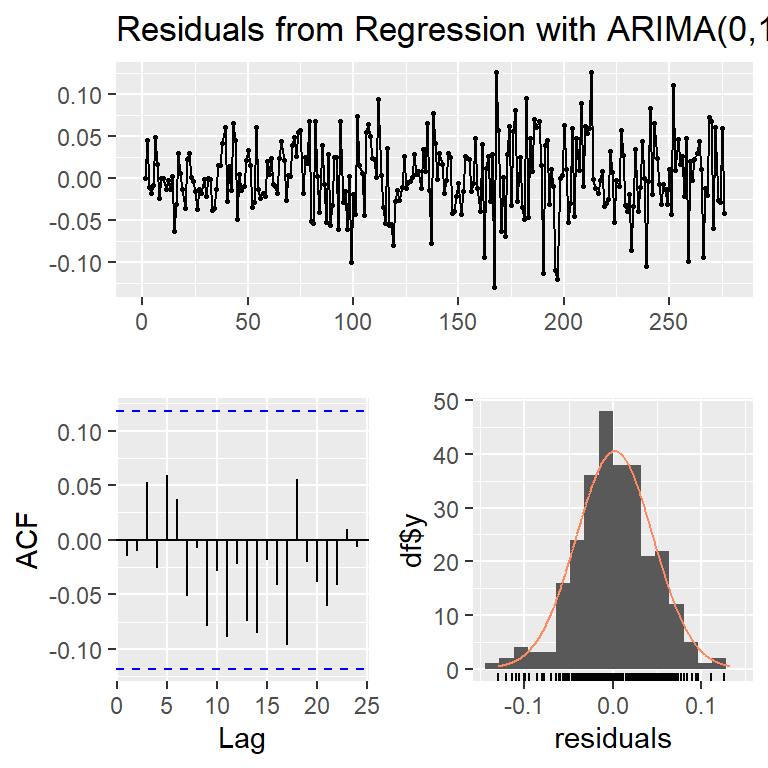
Análisis de intervención
- De manera formal, un modelo de intervención se define como \[Z_t = m_t + N_t,\] donde \(N_t \sim ARIMA(p,d,q)\) (Podría ser SARIMA).
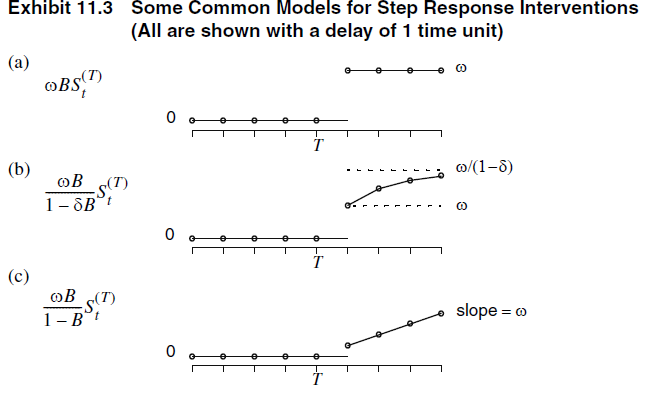
- Una intervención que produce un cambio inmediato y permanente, se puede modelar con
\[m_t = \omega S_t^{(T)},\]
donde \(S_t^{(T)}\) es una función escalonada \[S_t^{(T)} = \begin{cases} 1, & t \geq T, \\ 0, & t < T. \end{cases}\]
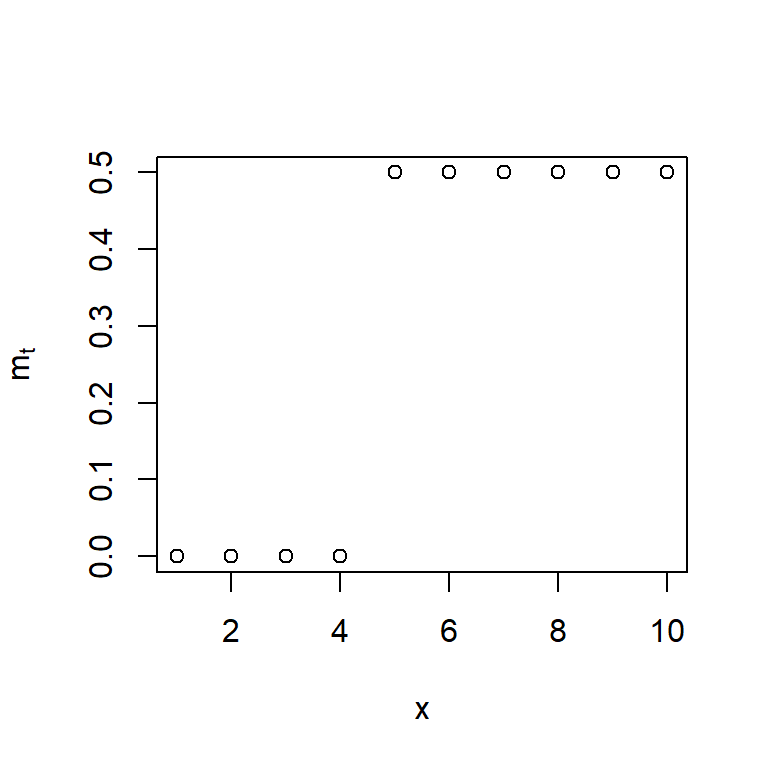
- Note que es posible establecer un efecto rezagado de período \(d\).
\[m_t = \omega S_{t-d}^{(T)}=\omega B^d S_{t}^{(T)},\]
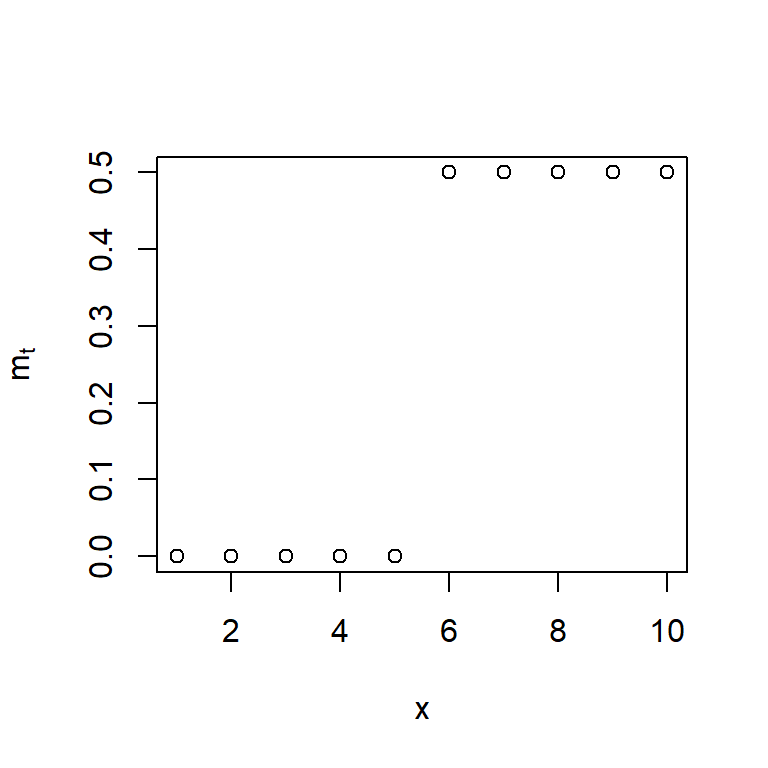
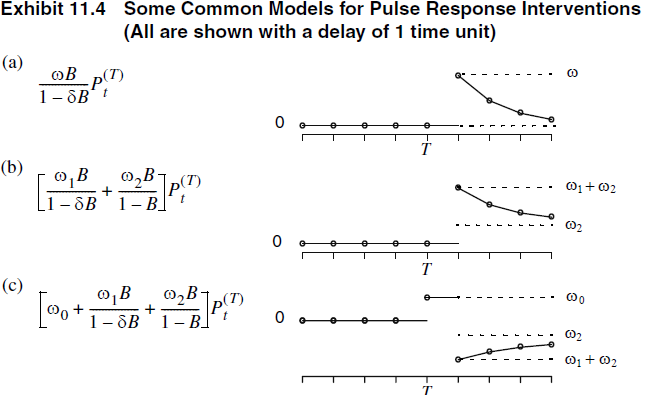
- Otro tipo de intervención produce solamente un cambio inmediato en el tiempo \(t\):
\[m_t = \omega P_t^{(T)},\]
donde \(P_t^{(T)} = S_t^{(T)} - S_{t-1}^{(T)}\) es una función de impulso. \[P_t^{(T)} = \begin{cases} 1, & t = T, \\ 0, & t \neq T. \end{cases}\]
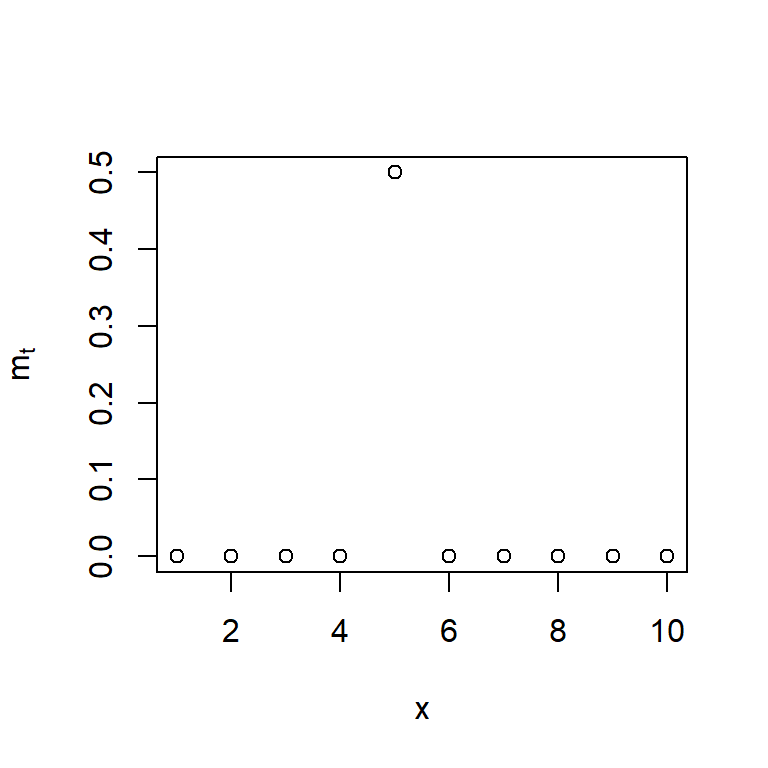
- Otros tipos de intervención se puede incorporar con la especificación de una ecuación tipo AR(1) y con \(d=1\):
\[m_t = \delta m_{t-1} + \omega S_{t-1}^{(T)},\] con la condición inicial de \(m_0=0\).
- Se puede mostrar que con el uso del operador de rezago \(B\), se puede escribir como
\[m_t = \begin{cases} \omega \frac{1-\delta^{t-T}}{1-\delta}, & t > T, \\ 0, & t \leq T. \end{cases}\]
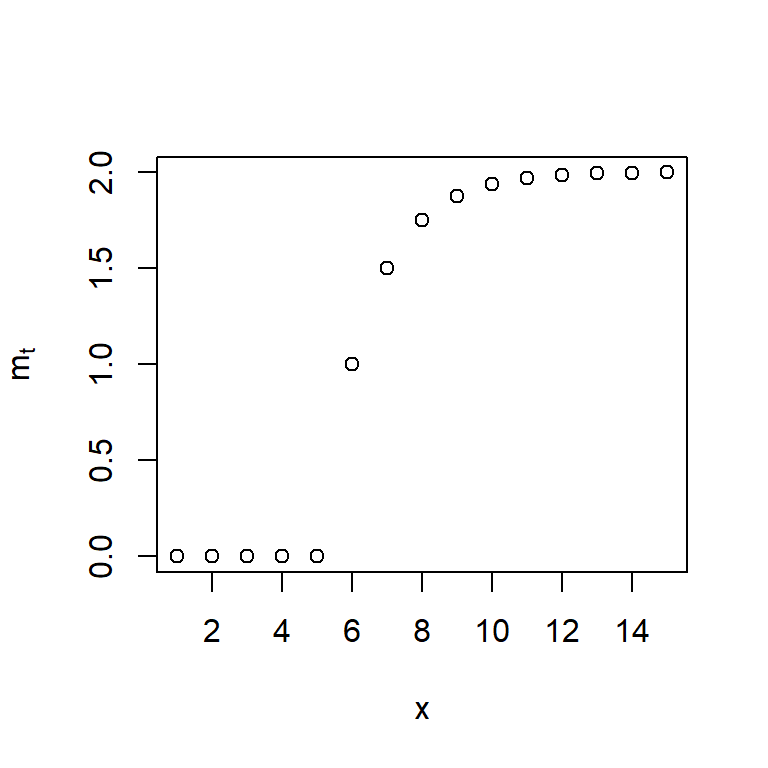
- De igual forma, se puede incorporar con la especificación de una ecuación tipo AR(1) y con \(d=1\) a \(P_{t}^{(T)}\):
\[m_t = \delta m_{t-1} + \omega P_{t-1}^{(T)},\] con la condición inicial de \(m_0=0\).
- Con el uso del operador de rezago \(B\), se puede escribir como
\[m_t =\omega \frac{B}{1-\delta B} P_{t}^{(T)} \]
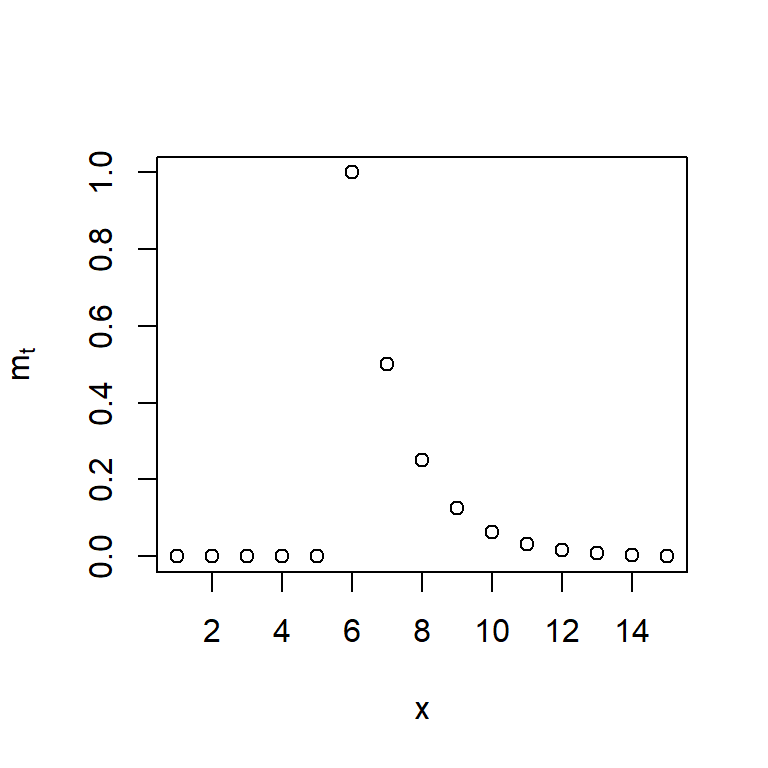
- En general, se puede modelar la función de media \(m_t\) usando un modelo similar a ARMA:
\[ \phi(B) m_t = \theta(B) P_{t}^{(T)},\] o bien \[ m_t = \frac{\theta(B)}{\phi(B)} P_{t}^{(T)}.\]
- Note que se puede usar tanto la función \(P_{t}^{(T)}\) o \(S_{t}^{(T)}\) para representar el cambio pues \(P_{t}^{(T)}= (1-B)S_{t}^{(T)}\).
Fuente: Capítulo 11 del Cryer & Chan (2008) Time Series Analysis with Applications in R.
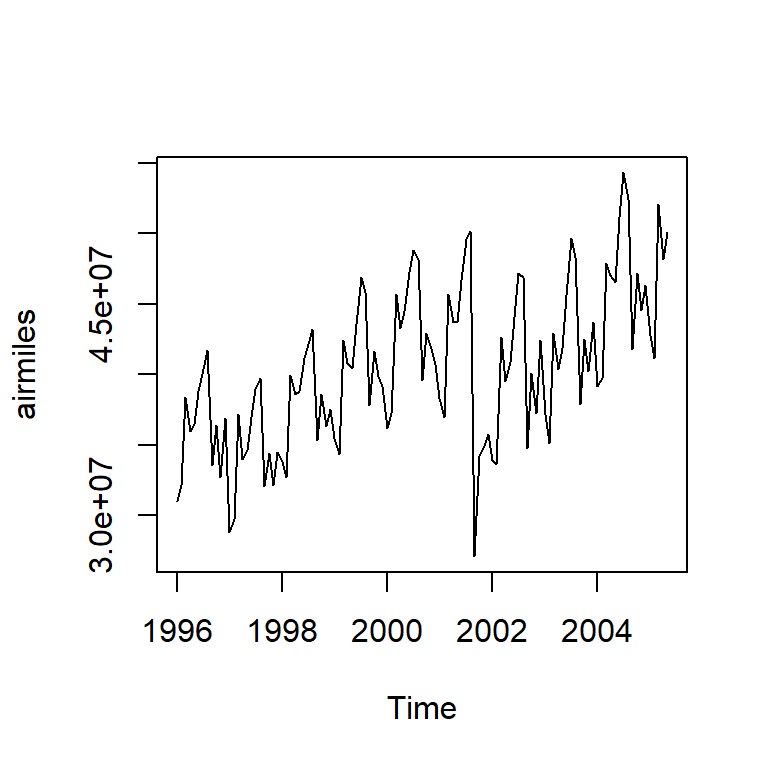
Ejemplo de millas mensuales de pasajeros
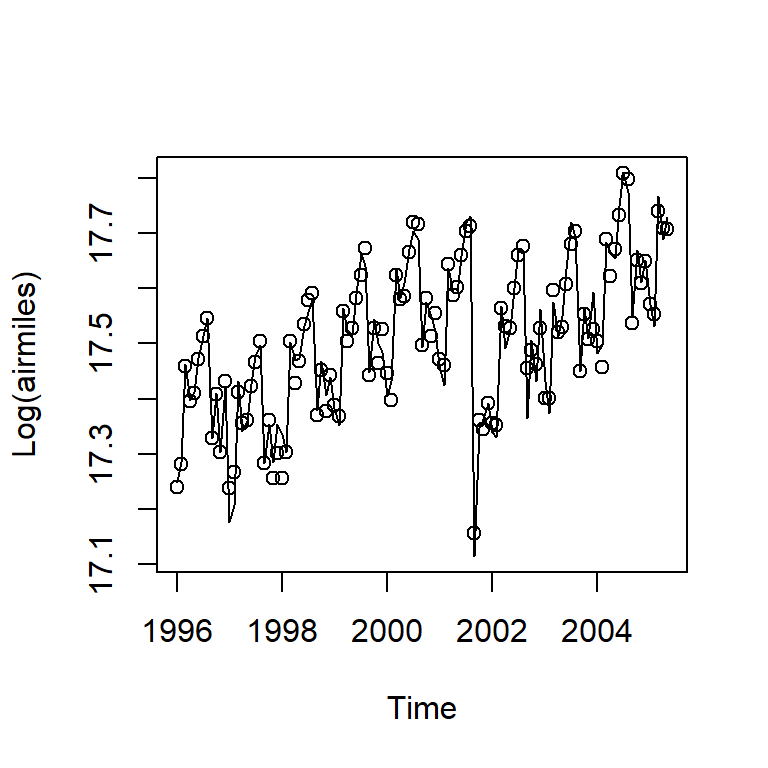
- Los datos se tratan de las millas mensuales de pasajeros de aerolíneas en los E.U de enero 1996 a mayo de 2005.
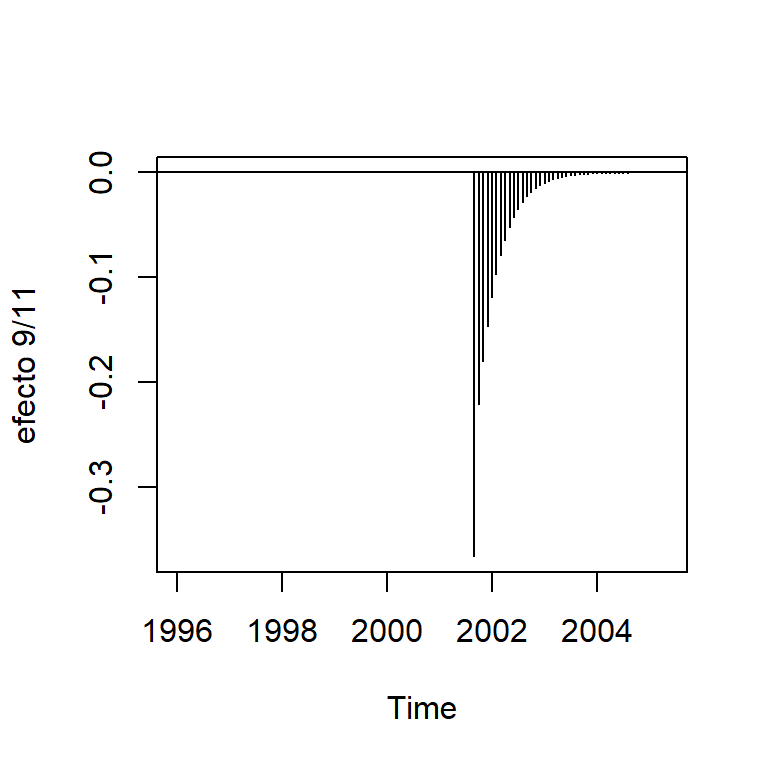
Los ataques terroristas en septiembre 2001 causó un efecto instantáneo (negativo) y lentamente se recupera a lo largo del período.
Por lo que este modelo para intervención es utilizado \[m_t = \omega_0 P_t^{(T)} + \frac{\omega_1}{1-\omega_2 B}P_t^{(T)},\] donde \(T\) es septiembre de 2001. \(\omega_0+\omega_1\) representa el efecto del mes y \(\omega_1 \omega_2^k, k=0,1,2,...\) representa el efecto de decaimiento exponencial.
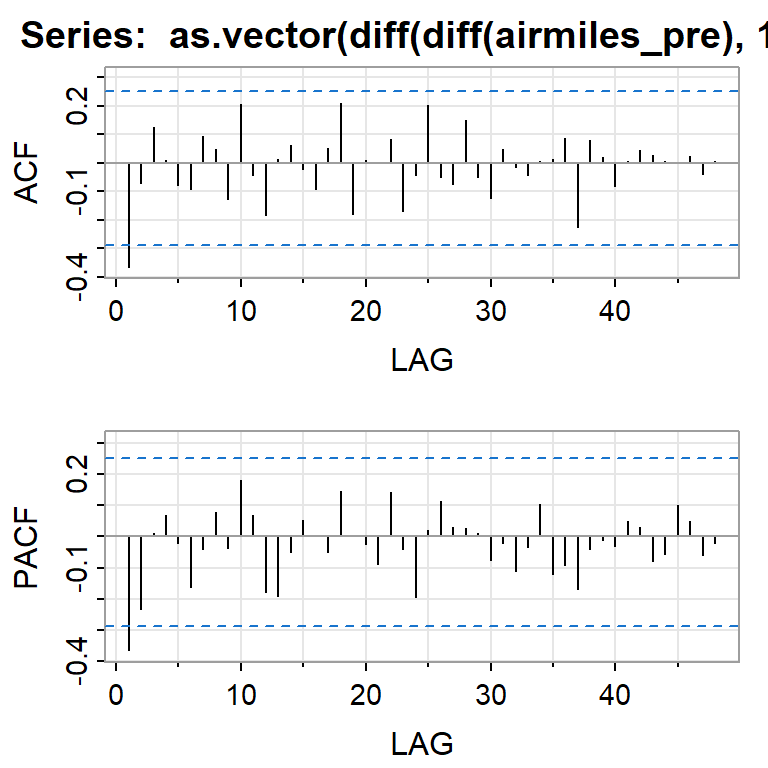
- Usando los datos antes de la intervención, un \(SARIMA(0,1,1)(0,1,0)_{12}\) es identificado.
- Después de la estimación y diagnósticos, se volvió a identificar un componente de SMA(1) que resulta ser relevante.
- Definición de las intervenciones y períodos con valores extremos.
- Estimación del modelo:
air.m1=arimax(log(airmiles),order=c(0,1,1),
seasonal=list(order=c(0,1,1),period=12),
xtransf=xtransf,transfer=list(c(0,0), # efecto instantáneo
c(1,0)), # efecto AR(1)
xreg=xreg,
method='ML')
air.m1
Call:
arimax(x = log(airmiles), order = c(0, 1, 1), seasonal = list(order = c(0, 1,
1), period = 12), xreg = xreg, method = "ML", xtransf = xtransf, transfer = list(c(0,
0), c(1, 0)))
Coefficients:
ma1 sma1 Dec96 Jan97 Dec02 I911-MA0 I911.1-AR1
-0.3825 -0.6499 0.0989 -0.0690 0.0810 -0.0949 0.8139
s.e. 0.0926 0.1189 0.0228 0.0218 0.0202 0.0462 0.0978
I911.1-MA0
-0.2715
s.e. 0.0439
sigma^2 estimated as 0.0006721: log likelihood = 219.99, aic = -423.98