Tema 8: Modelos no lineales: ARCH, GARCH y extensiones
Paquetes de R
Para este tema, se necesita cargar estos paquetes:
Introducción
Contenido
Introducción
ARCH
GARCH
Introducción
- En la práctica, se observan fenómenos con variancia condicional que evoluciona con el tiempo y los modelos ARIMA no son adecuados para estos fenómenos.
- La aplicación más utilizada y conocida es en las series financieras.
- Existe una variedad de modelos no lineales en la literatura.
- Vamos a enfocarnos en la clase de modelos GARCH:
- ARCH (AutoRegressive Conditional Heteroscedastic): Modelos autoregresivos con heteroscedasticidad condicional.
- GARCH (Generalized AutoRegressive Conditional Heteroscedastic): Modelos autoregresivos con heteroscedasticidad condicional generalizada.
- Extensiones del modelo GARCH: EGARCH y TGARCH.
Algunos modelos no lineales
- De manera general, el análisis de modelos no lineales suponen que los errores o innovaciones \(a_t\) son i.i.d. y el modelo tiene la siguiente forma: \[X_t= g(a_{t-1},a_{t-2},...)+a_{t}h(a_{t-1},a_{t-2},...),\] en donde
- \(g(\cdot)\) es la media condicional, y
- \(h^2(\cdot)\) es la variancia condicional.
- Se dice que el modelo es
- no lineal en media, si \(g(\cdot)\) es no lineal.
- no lineal en variancia, si \(h^2(\cdot)\) es no lineal.
Ejemplo 1
Los modelos ARMA (bajo el supuesto de estacionariedad) pueden ser representados por: \[X_t= \sum\limits_{i=0}^\infty \xi_i a_{t-i} = \sum\limits_{i=1}^\infty \xi_i a_{t-i} + a_{t}\]
Note que \(g(\cdot)=\sum\limits_{i=0}^\infty \xi_i a_{t-i}\) y \(h(\cdot)=1\) son lineales. Entonces, un modelo ARMA es lineal.
Ejemplo 2
- El modelo: \[X_t=a_t+\alpha a_{t-1}^2\] es no lineal en media porque \(g(\cdot)=\alpha a_{t-1}^2\) y lineal en variancia \(h(\cdot)=1\).
Ejemplo 3
- El modelo ARCH(1) \[X_t= a_t \sqrt{\alpha X_{t-1}^2}\] es no lineal en variancia porque \(g(\cdot)=0\) y \(h(\cdot)=\sqrt{\alpha X_{t-1}^2}\) y \(X_{t-1}\) depende de \(a_{t-1}\).
Ejemplo 4
- Modelos polinomiales tienen la función \(g(\cdot)\) como
\[g(a_{t-1},a_{t-2},...)=\sum\limits_{i=1}^\infty c_i a_{t-i}+\sum\limits_{i=1}^\infty \sum\limits_{j=1}^\infty b_{ij} a_{t-i} a_{t-j}+...,\] Es una expansión de Volterra, involucrando términos lineales, bilineales,… de las innovaciones.
Los modelos ARCH
Los modelos ARCH (AutoRegressive Conditional Heteroscedastic), o modelos autorregresivos con heteroscedasticidad condicional, fueron propuestos por Engle (1982).
Robert F. Engle recibió Premio Nobel de Economía por los análisis de ARCH para datos de series temporales económicos.
La idea básica del modelo es un proceso estacionario que tienen la variancia marginal constante, pero la variancia condicionada a sus valores pasados no lo es.
Estos procesos fueron propuestos para explicar ciertas propiedades que no pueden ser explicados por los modelos ARIMA y que son muy frecuentes en datos financieros y ambiantales de alta frecuencia (datos diarios, horarios, etc.).
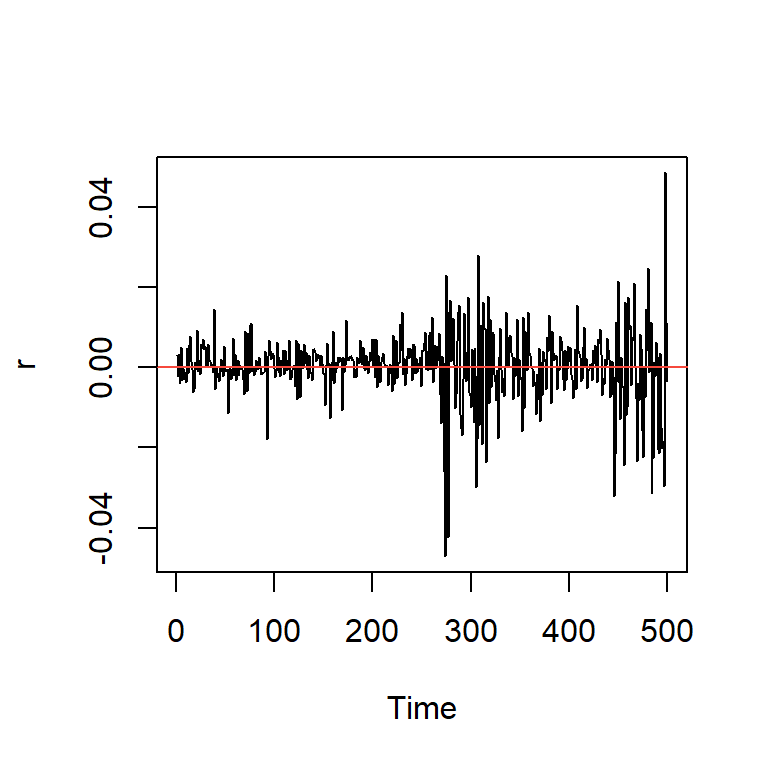
Retornos
- Suponga que \(X_t\) es el valor de un activo en el tiempo \(t\), el retorno \(r_t\) en el tiempo \(t\) es:
\[r_t=\frac{X_t-X_{t-1}}{X_{t-1}}\]
- Despejando la expresión anterior:
\[X_t=(1+r_t)X_{t-1}\] \[\Rightarrow \ln X_t=\ln (1+r_t)+ \ln X_{t-1}\] \[\Rightarrow \nabla \ln X_t = \ln X_t - \ln X_{t-1}=\ln (1+r_t) \approx r_t,\] si \(r_t\) son cambios porcentuales pequeños.
Nota
- Recuerde que para una función \(f(x)\), el polinomio de Taylor es una aproximación polinómica de una función n veces derivable en un punto \(a\). Concretamente:
\[f(x) \approx f(a) + f'(a) (x-a) + \frac{f''(a)}{2!}(x-a)^2 + ...+ \frac{f^{(n)}(a)}{n!}(x-a)^n\]
De esta forma, \[\nabla \ln X_t = \ln X_t - \ln X_{t-1}=\ln (1+r_t) = f(r_t) \approx r_t,\]
A partir de aquí, llamamos \(r_t\) o \(\nabla \ln X_t\) como retornos.
En finanzas, la variancia condicional del retorno financiero de una cartera es una medida de riesgo de una cartera (Value at Risk - VaR).
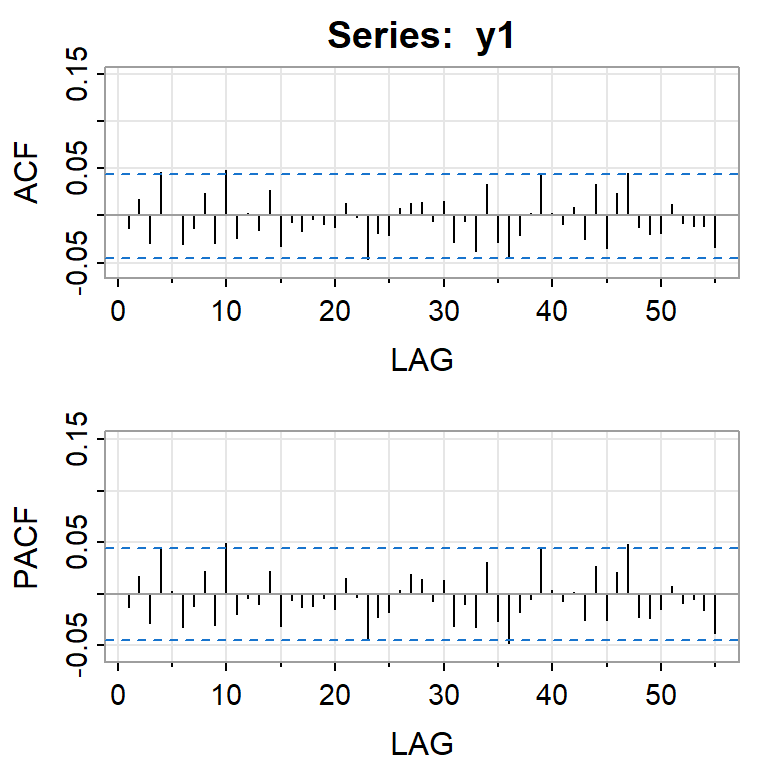
En un mercado eficiente, el retorno esperado debería ser cero, y así debería comportarse como un proceso de ruido blanco.
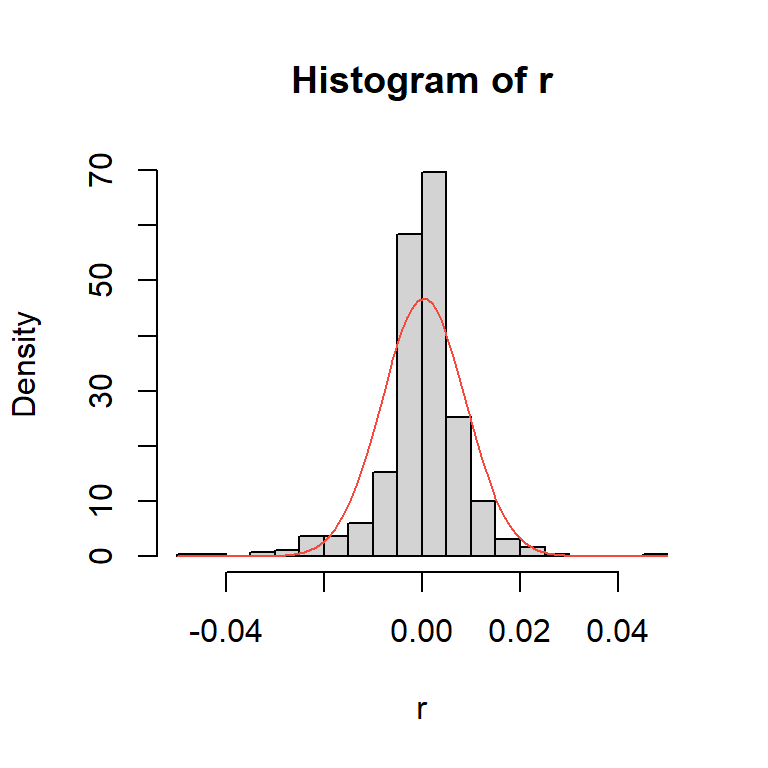
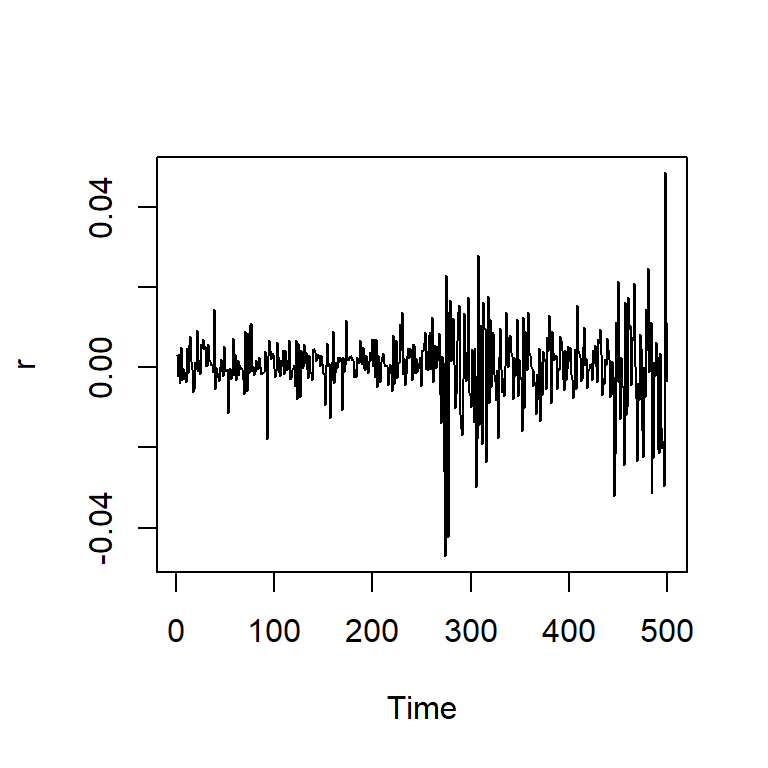
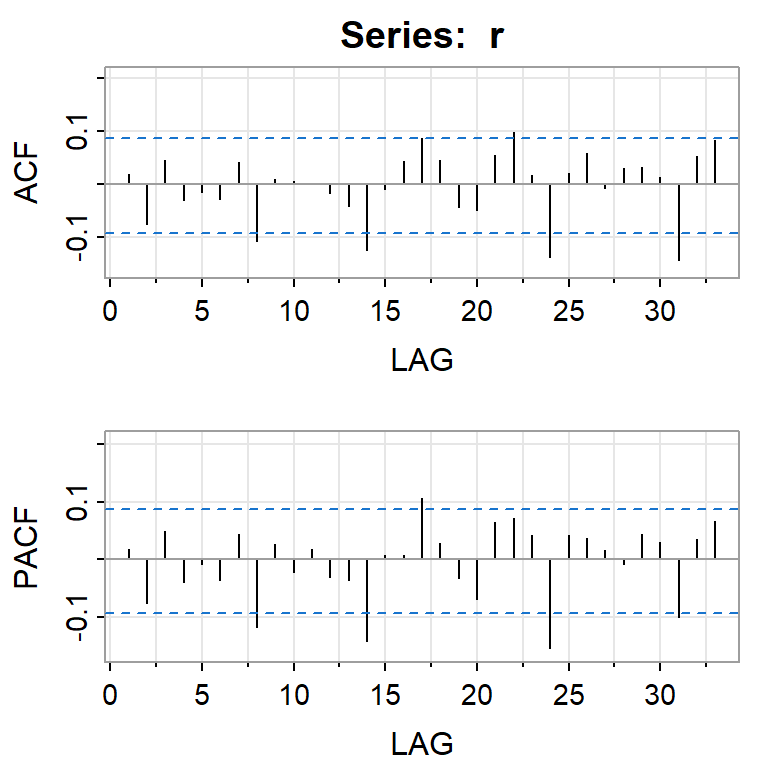
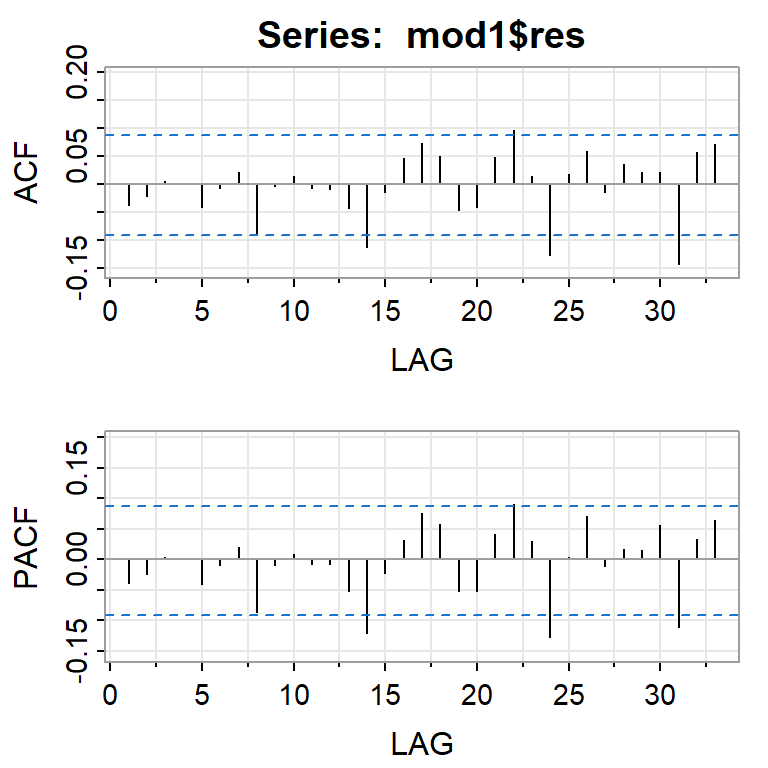
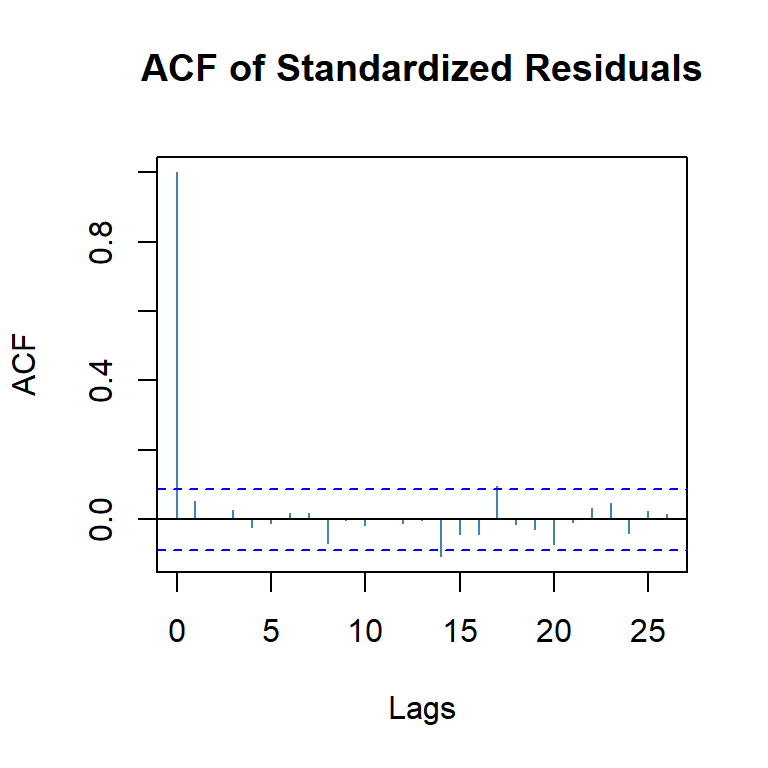
Ejemplo: promedio diario industrial Dow Jone
[1] "DJI"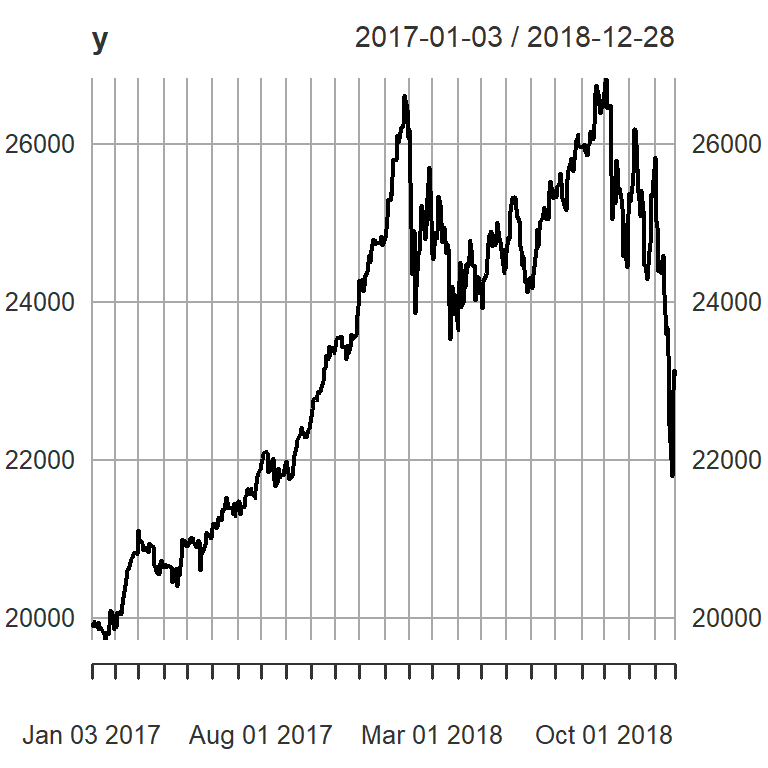
[,1] [,2] [,3] [,4] [,5] [,6] [,7] [,8] [,9] [,10] [,11] [,12] [,13]
ACF 0.02 -0.07 0.05 -0.03 -0.02 -0.03 0.04 -0.11 0.01 0.01 0.00 -0.02 -0.04
PACF 0.02 -0.08 0.05 -0.04 -0.01 -0.04 0.04 -0.12 0.03 -0.02 0.02 -0.03 -0.03
[,14] [,15] [,16] [,17] [,18] [,19] [,20] [,21] [,22] [,23] [,24] [,25]
ACF -0.12 -0.01 0.04 0.09 0.05 -0.04 -0.05 0.05 0.10 0.02 -0.14 0.02
PACF -0.14 0.01 0.01 0.11 0.03 -0.03 -0.07 0.06 0.07 0.04 -0.15 0.04
[,26] [,27] [,28] [,29] [,30] [,31] [,32] [,33]
ACF 0.06 -0.01 0.03 0.03 0.01 -0.14 0.05 0.08
PACF 0.04 0.02 -0.01 0.04 0.03 -0.10 0.04 0.07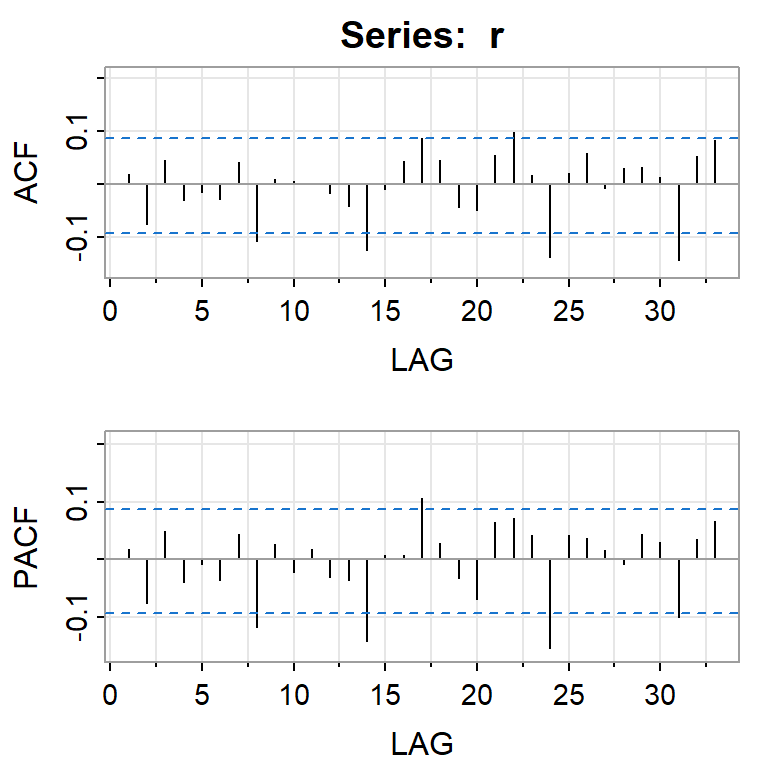
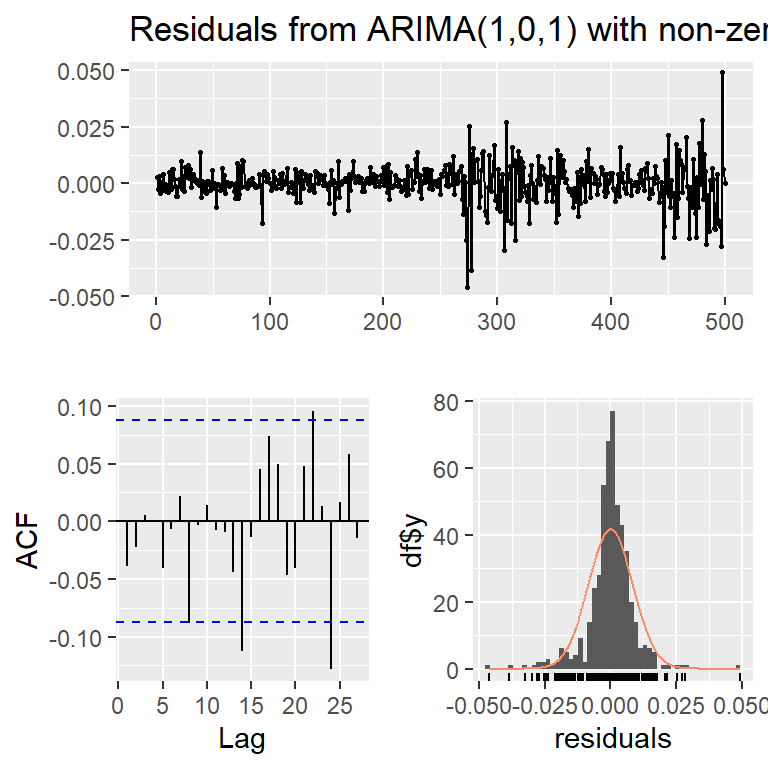
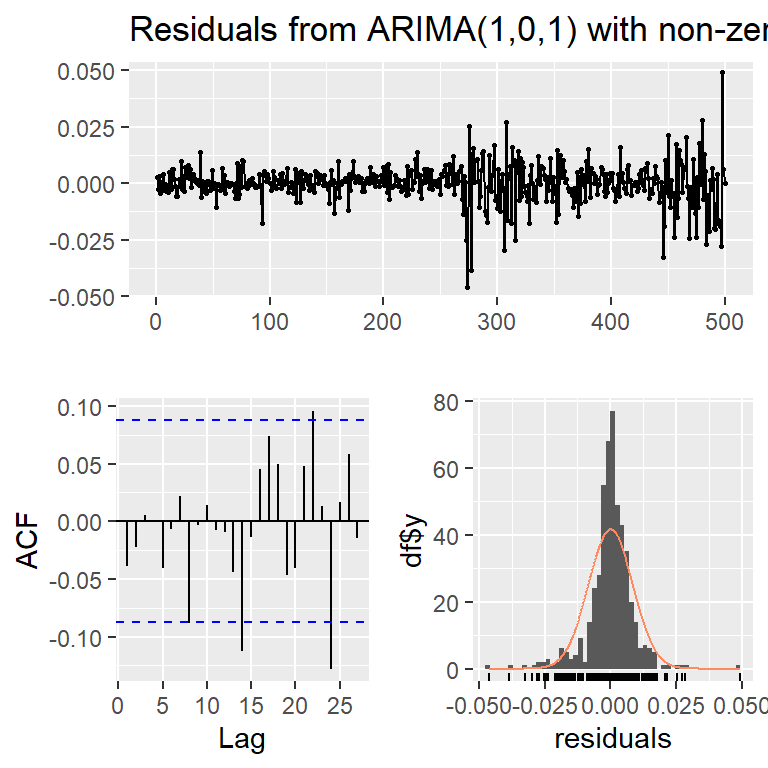
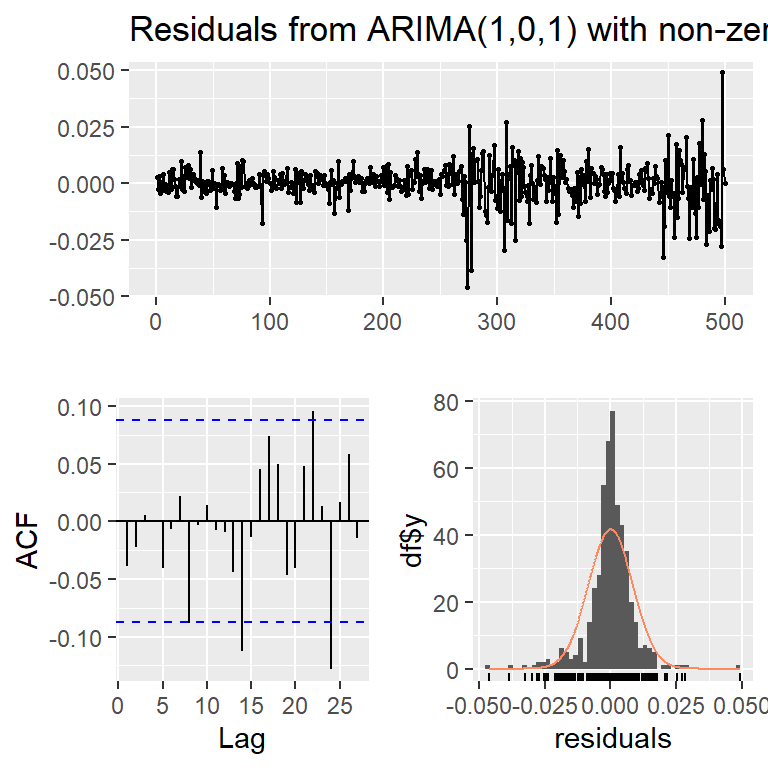
Series: r
ARIMA(1,0,1) with non-zero mean
Coefficients:
ar1 ma1 mean
-0.8613 0.9456 3e-04
s.e. 0.0418 0.0259 4e-04
sigma^2 = 7.121e-05: log likelihood = 1679.38
AIC=-3350.76 AICc=-3350.68 BIC=-3333.9
Training set error measures:
ME RMSE MAE MPE MAPE MASE
Training set 1.210921e-05 0.008413378 0.005502822 98.24685 154.1698 0.7121837
ACF1
Training set -0.03847749ARCH
Contenido
Introducción
ARCH
GARCH
ARCH
- Modelo ARCH(1):
\[X_t=\sqrt{h_t} \epsilon_t\] \[h_t= \alpha_0 +\alpha_1 X_{t-1}^2\] en donde \(\epsilon_t\) es ruido blanco gaussiano estándar, i.e. \(\epsilon_t \overset{iid}{\sim} N(0,1)\), y \(\alpha_0>0,\alpha_1 \geq 0\).
- La distribución condicional de \(X_t\) dado \(X_{t-1}\) es
\[X_t|X_{t-1} \sim N(0,\alpha_0 +\alpha_1 X_{t-1}^2)\]
Recordatorio
Las propiedades de la esperanza y variancia condicional. \[E[Y]=E[E(Y|X)]~~y~~Var[Y]=E[Var(Y|X)]+Var[E(Y|X)]\]
Defina \(\mathcal{F}_s= \left\lbrace X_{s},X_{s-1},... \right\rbrace\) como la información disponible hasta el período \(s\). Podemos calcular la media, variancia y autocorrelación incondicional de la serie:
Propiedades:
- \(E(X_t)=E \left\lbrace E \left[ X_t| \mathcal{F}_{t-1} \right] \right\rbrace=0\)
- \(Var(X_t)= E(X_t^2)=E \left\lbrace E \left[ X_t^2| \mathcal{F}_{t-1} \right] \right\rbrace=E(\alpha_0+\alpha_1 X_{t-1}^2)\) \(=\alpha_0+\alpha_1 E(X_{t-1}^2)\)
Si el proceso es estacionario, entonces para todo \(t\), \(E(X_{t}^2)=E(X_{t-1}^2)=Var(X_t)\) \[\Rightarrow Var(X_t)=\frac{\alpha_0}{1-\alpha_1}\] con \(0 \leq \alpha_1<1\).
- Para la autocovariancia \(\gamma_X(t+k,t) = \mathrm{Cov}(X_{t+k}, X_t)\),
\[\begin{align} \mathrm{Cov}(X_{t+k}, X_t) &= E(X_{t+k} X_t), \quad k \ge 1, \\ &= E\!\left\{ E\!\left[ X_{t+k} X_t \mid \mathcal{F}_{t+k-1} \right] \right\} \\ &= E\!\left\{ X_t\, E\!\left[ X_{t+k} \mid \mathcal{F}_{t+k-1} \right] \right\} \\ &= E\!\left\{ X_t\, E\!\left[ \sqrt{h_{t+k}}\, \epsilon_{t+k} \mid \mathcal{F}_{t+k-1} \right] \right\} \\ &= 0. \end{align}\]
Por lo tanto, \(\gamma_X(k)=0, k \geq 1\). En otras palabras, \(X_t\) es una secuencia de variables aleatorias no correlacionadas (ruido blanco) con variancia \(\frac{\alpha_0}{1-\alpha_1}\).
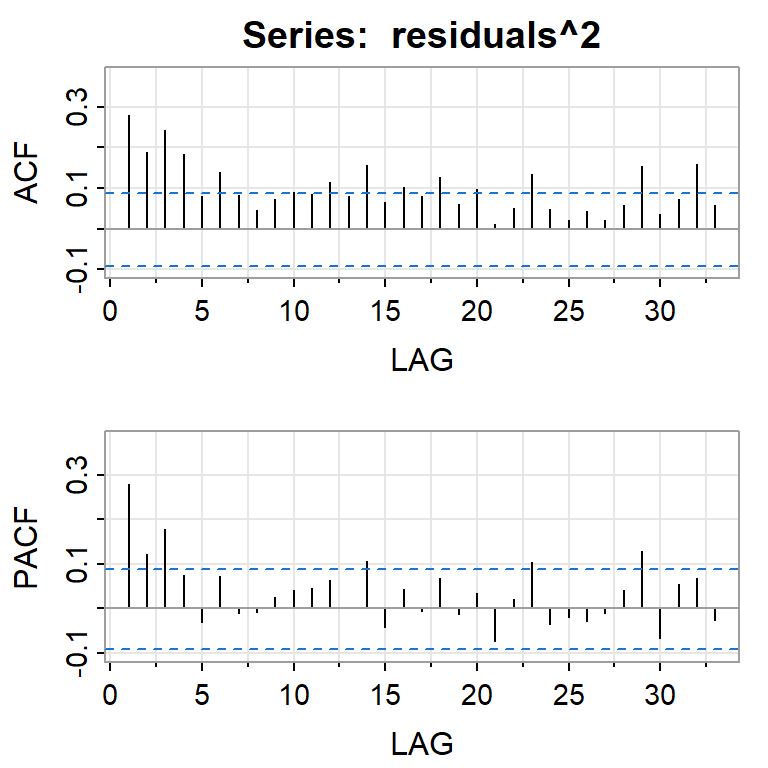
- Se puede demostrar que la kurtosis es \[K=3\frac{1-\alpha_1^2}{1-3 \alpha_1^2}>3.\] El modelo ARCH(1) es leptocúrtico ya que las colas son más pesadas que una distribución normal.
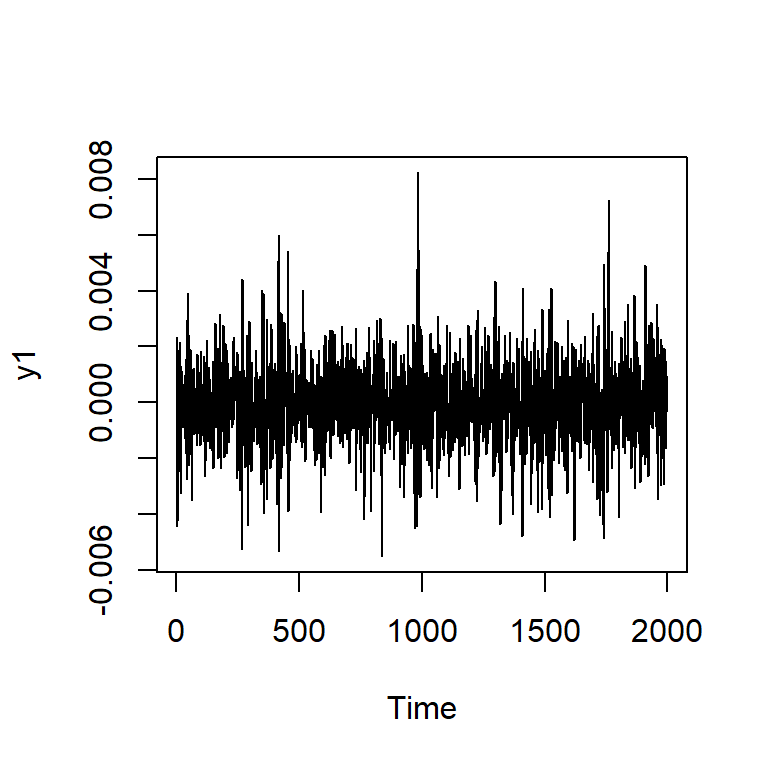
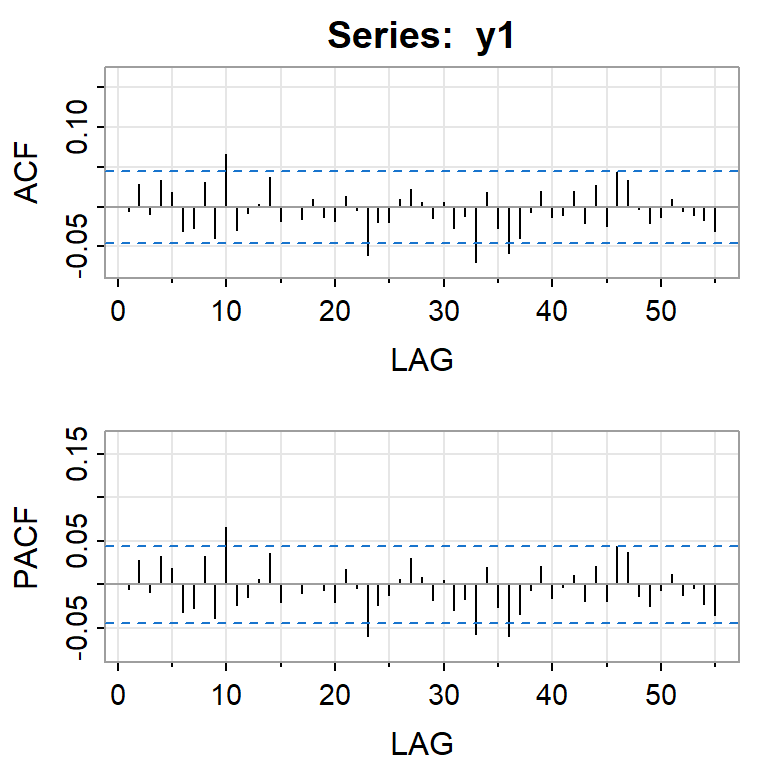
Simulación de ARCH(1) con \(\alpha_0=0.01\), \(\alpha_1=0.8\)
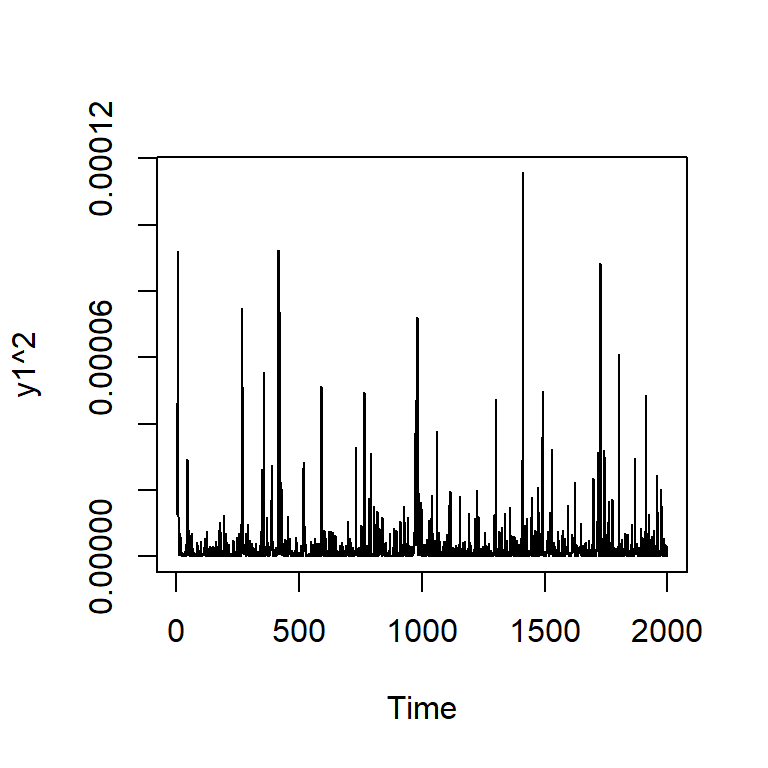
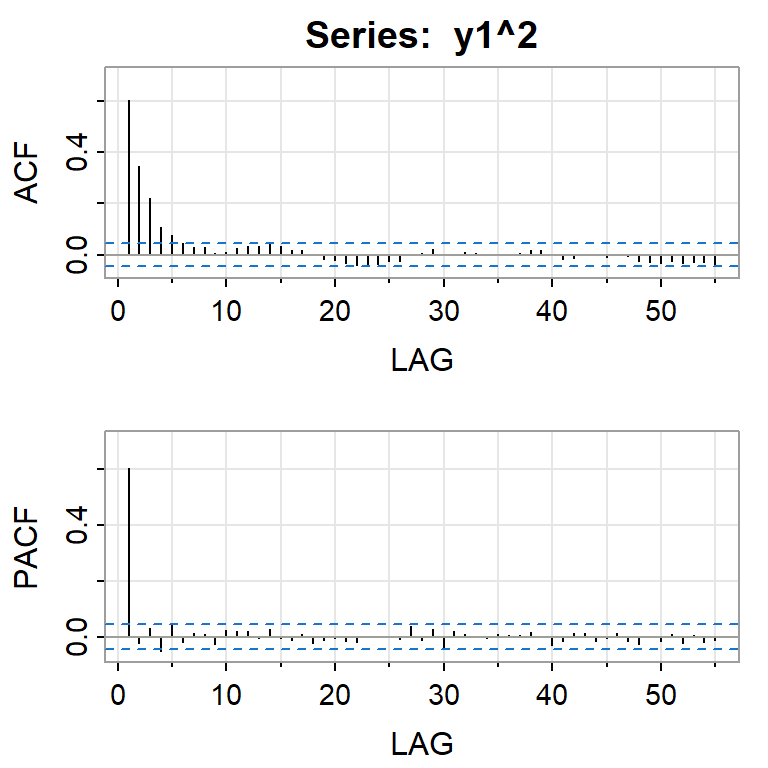
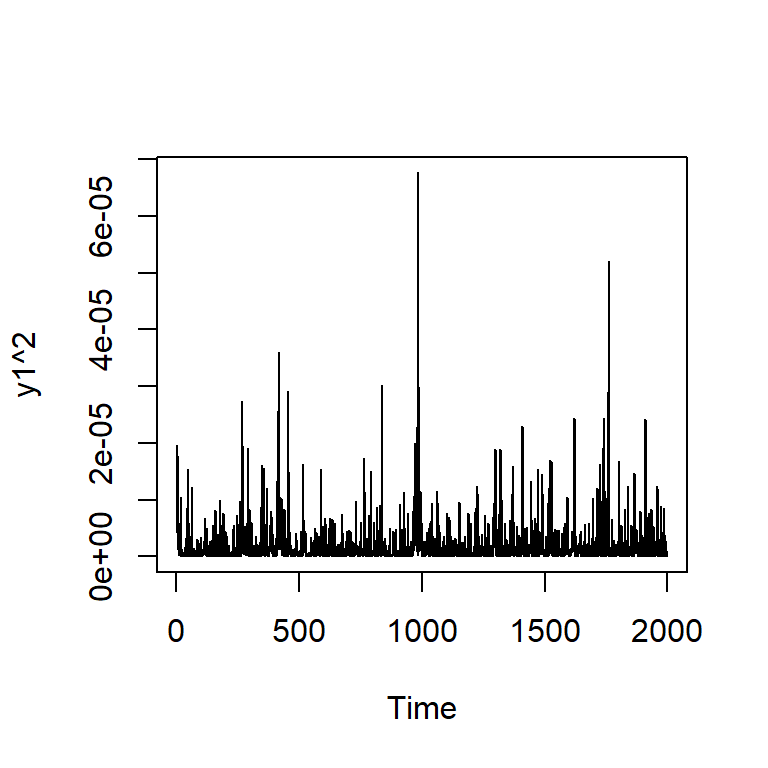
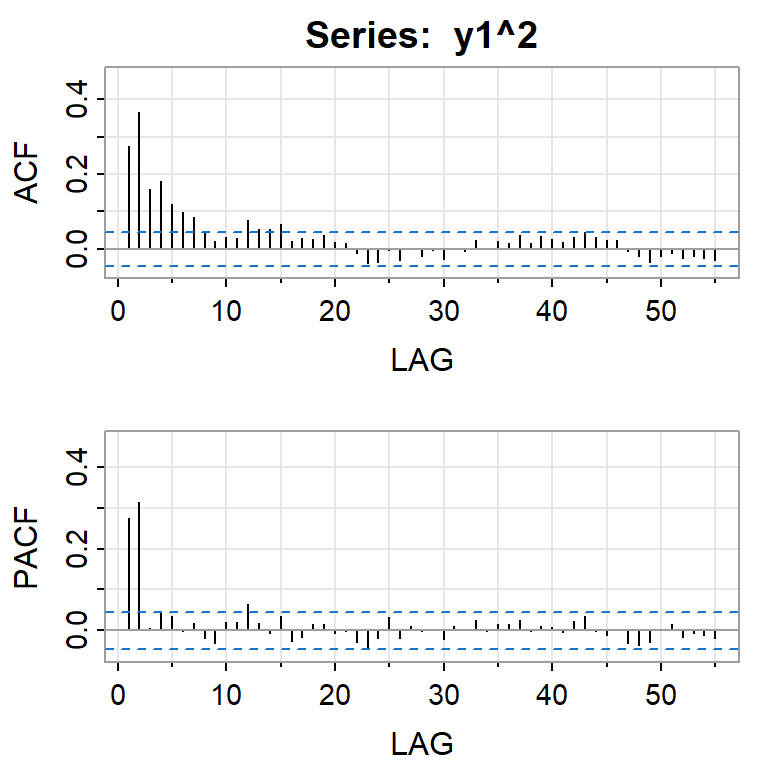
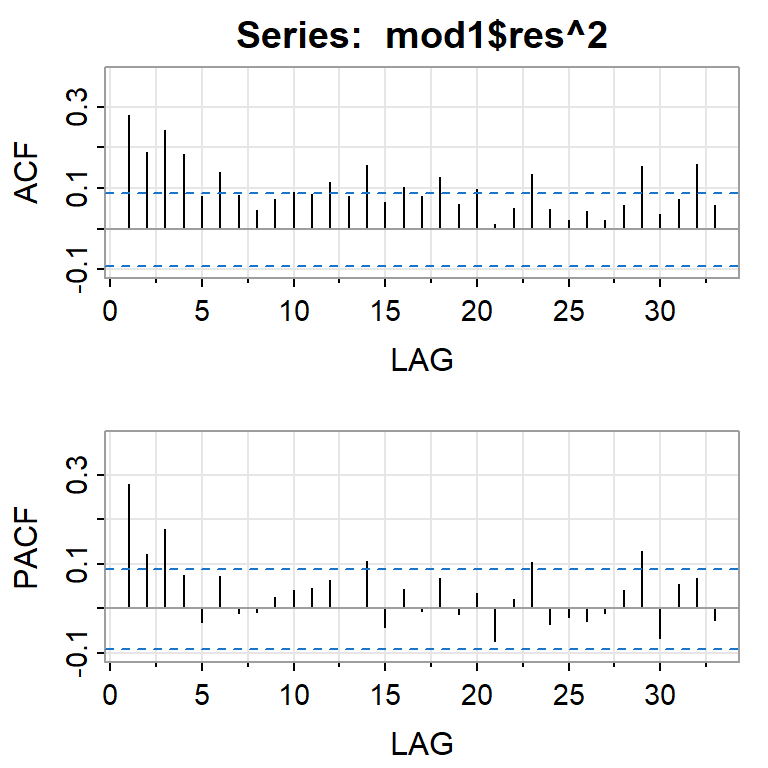
Si elevamos al cuadrado la serie simulada \(X_t\).
- Modelo ARCH(r):
\[X_t=\sqrt{h_t} \epsilon_t\] \[h_t= \alpha_0 +\alpha_1 X_{t-1}^2+\alpha_2 X_{t-2}^2+...+\alpha_r X_{t-r}^2\] en donde \(\epsilon_t\) es ruido blanco gaussiano estándar, i.e. \(\epsilon_t \overset{i.i.d.}{\sim} N(0,1)\), y \(\alpha_0 >0\) y \(\alpha_i \geq 0,i=1,...,r\).
Simulación de ARCH(2) con \(\alpha_0=0.01\), \(\alpha_1=0.2\), \(\alpha_2=0.4\)
Si elevamos al cuadrado la serie simulada \(X_t\).
GARCH
Contenido
Introducción
ARCH
GARCH
GARCH
El Modelo GARCH(1,1) es definido por:
\[X_t=\sqrt{h_t} \epsilon_t\] \[h_t= \alpha_0 + \alpha_1 X_{t-1}^2 + \beta_1 h_{t-1}\]
con \(\epsilon_t \overset{i.i.d.}{\sim} N(0,1)\), \(\alpha_0 >0\), \(\alpha_1 \geq 0\), \(\beta_1 \geq 0\) y \(\alpha_1+\beta_1 < 1\).
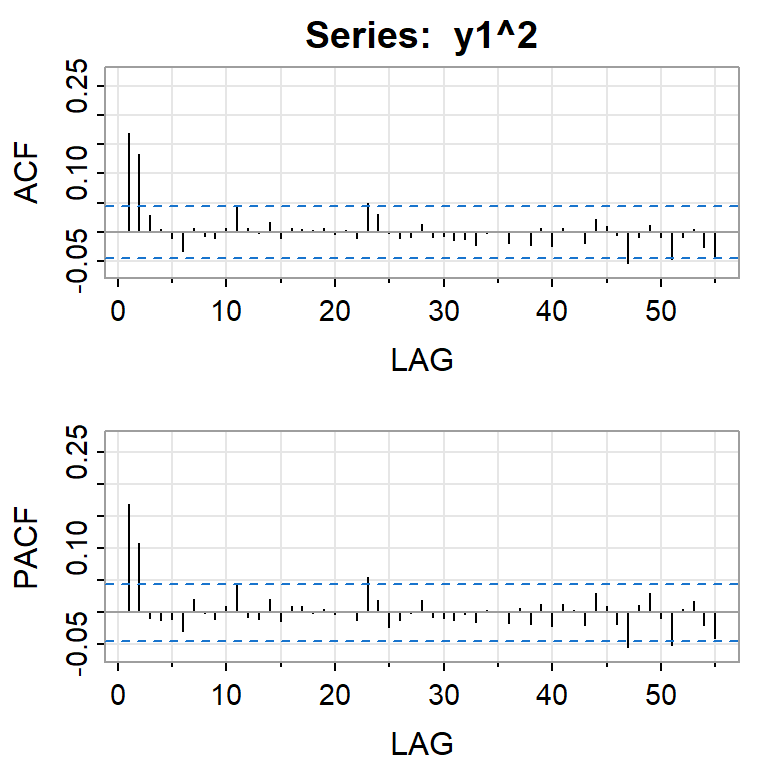
Simulación de GARCH(1,1) con \(\alpha_0=0.01\), \(\alpha_1=0.2\), \(\beta_2=0.4\)
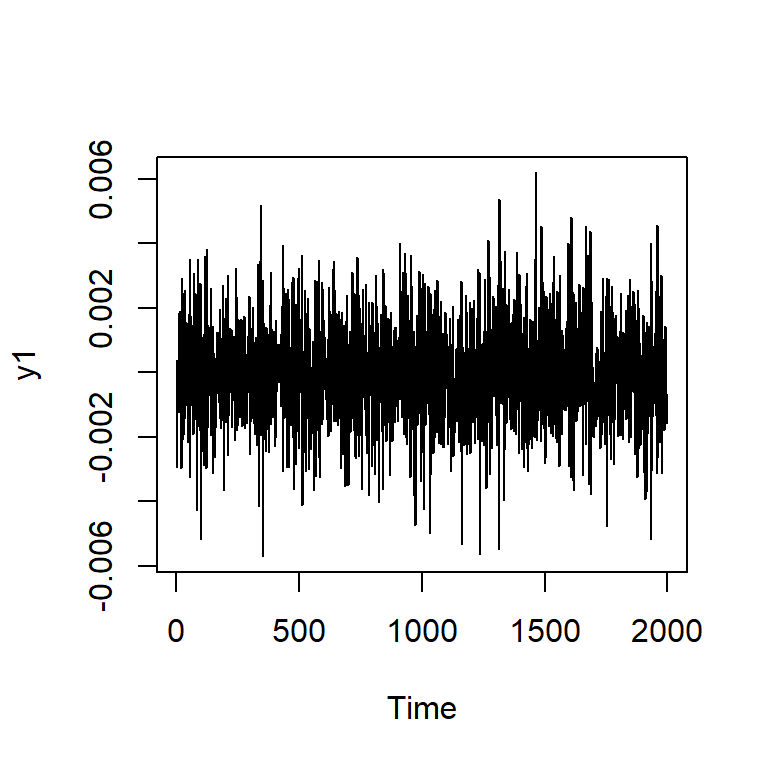
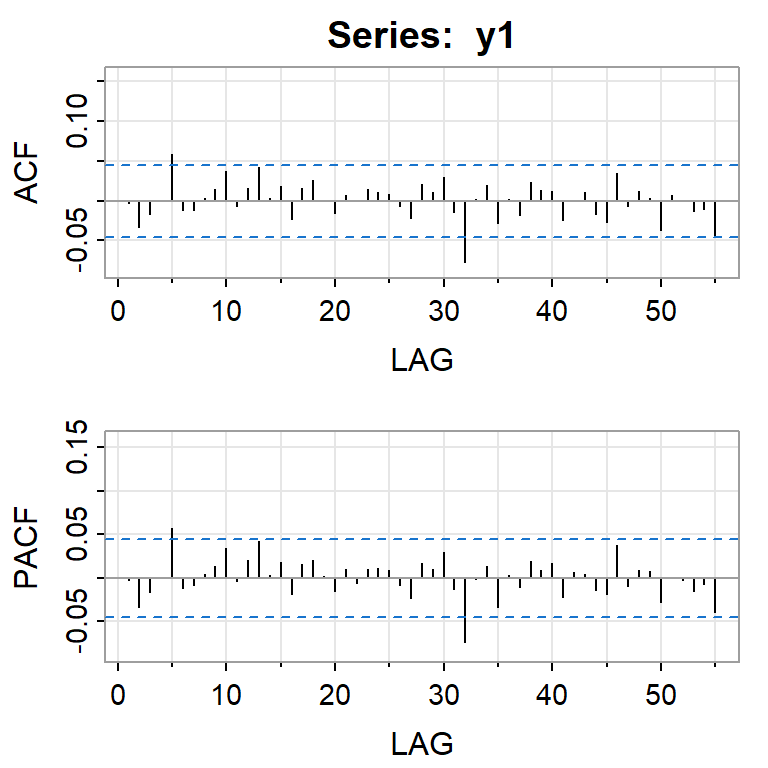
Si elevamos al cuadrado la serie simulada \(X_t\).
Ejemplo: promedio diario industrial Dow Jone
Series: r
ARIMA(1,0,1) with non-zero mean
Coefficients:
ar1 ma1 mean
-0.8613 0.9456 3e-04
s.e. 0.0418 0.0259 4e-04
sigma^2 = 7.121e-05: log likelihood = 1679.38
AIC=-3350.76 AICc=-3350.68 BIC=-3333.9
Training set error measures:
ME RMSE MAE MPE MAPE MASE
Training set 1.210921e-05 0.008413378 0.005502822 98.24685 154.1698 0.7121837
ACF1
Training set -0.03847749 Estimate Std. Error t value Pr(>|t|)
mu 1.500179e-03 6.579730e-04 2.280001 2.260763e-02
ar1 -5.868758e-01 5.305396e-01 -1.106187 2.686458e-01
ma1 5.889133e-01 5.449086e-01 1.080756 2.798056e-01
omega 1.737066e-06 7.635410e-07 2.275013 2.290513e-02
alpha1 1.598314e-01 4.003845e-02 3.991948 6.553261e-05
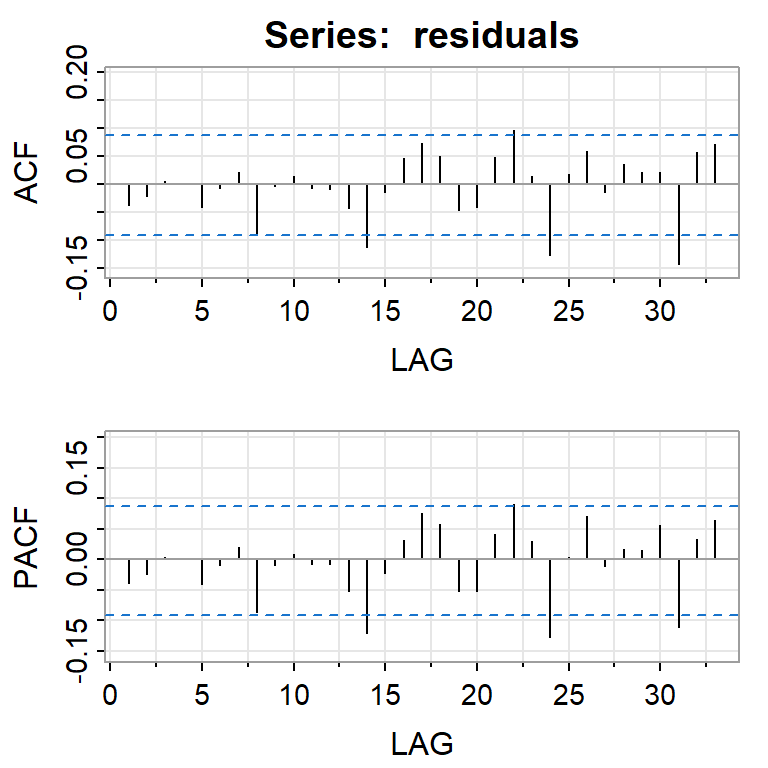
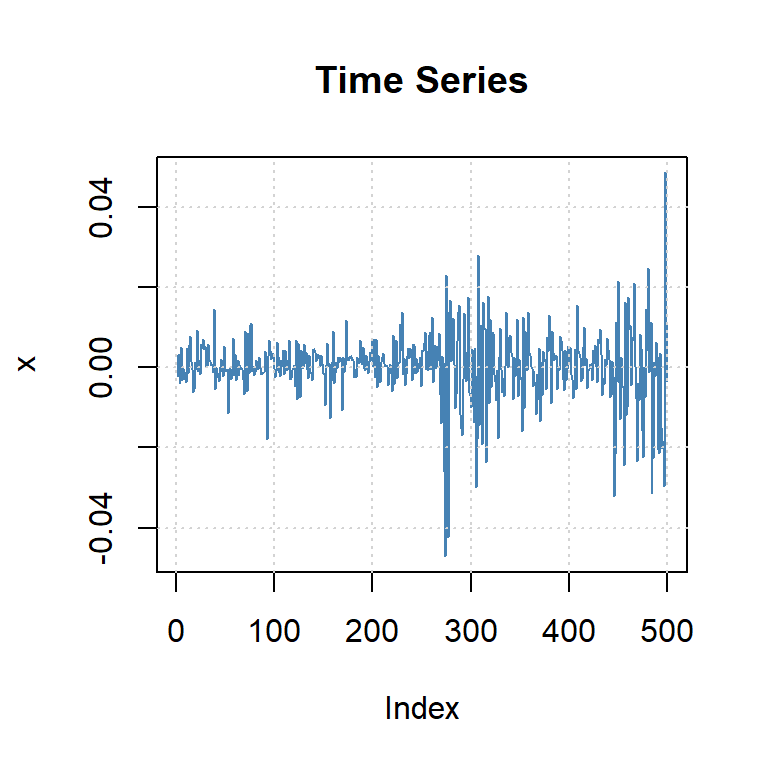
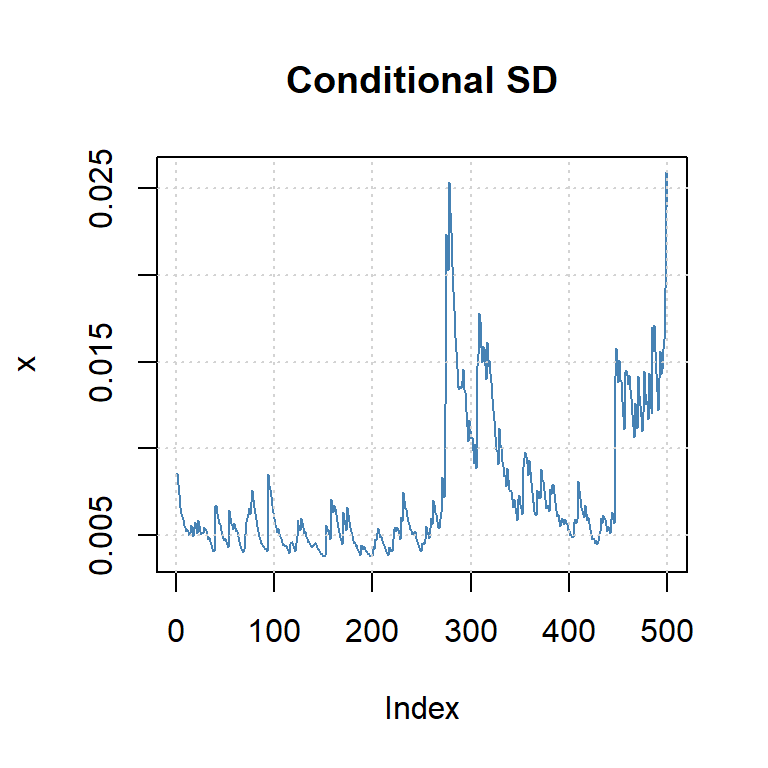
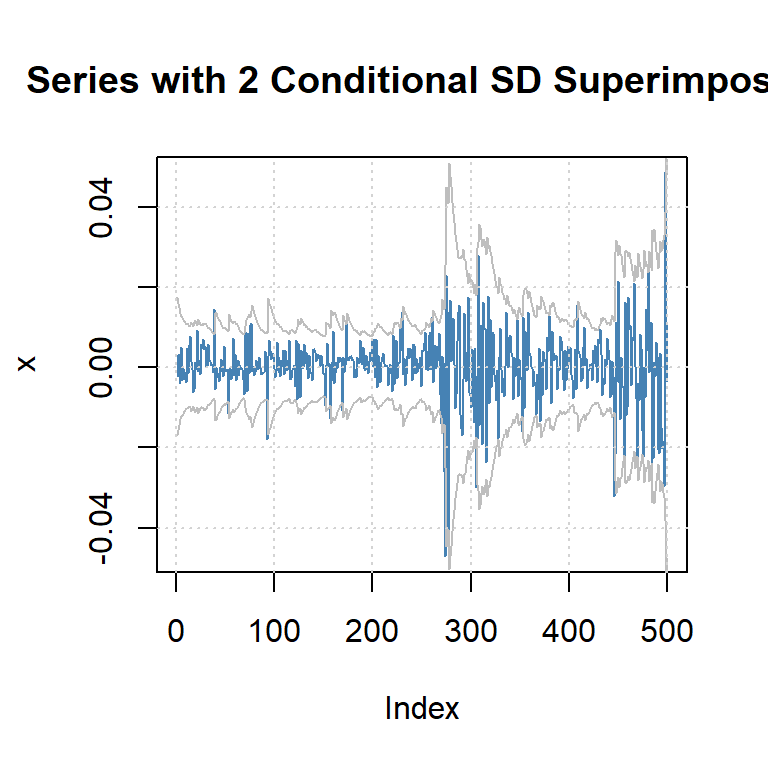
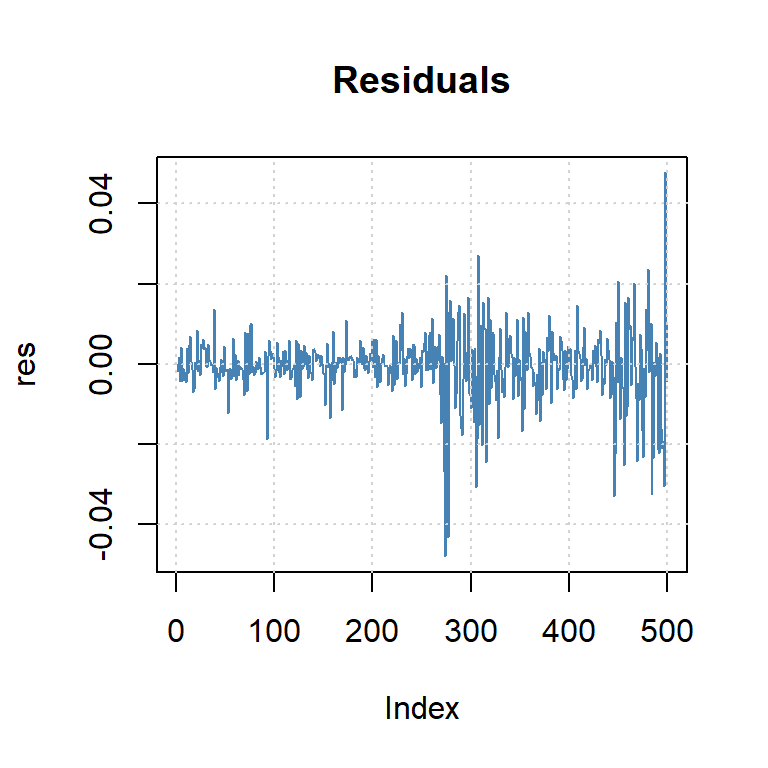
beta1 8.280899e-01 4.305972e-02 19.231194 0.000000e+00El Modelo ARMA(1,1)+GARCH(1,1):
\[r_t= 0.0015 -0.59 r_{t-1} + \varepsilon_t + 0.59 \varepsilon_{t-1}\] \[\varepsilon_t=\sqrt{h_t} \epsilon_t\] \[h_t= 0.0000017 + 0.16 \varepsilon_{t-1}^2 + 0.83 h_{t-1}\]
- Los coeficientes de la parte de ARMA no son significativos.
Estimate Std. Error t value Pr(>|t|)
mu 0.0015 0.0007 2.2800 0.0226
ar1 -0.5869 0.5305 -1.1062 0.2686
ma1 0.5889 0.5449 1.0808 0.2798
omega 0.0000 0.0000 2.2750 0.0229
alpha1 0.1598 0.0400 3.9919 0.0001
beta1 0.8281 0.0431 19.2312 0.0000- Lo ideal es eliminarlos del modelo.
Estimate Std. Error t value Pr(>|t|)
mu 0.0010 0.0003 3.6563 0.0003
omega 0.0000 0.0000 2.2971 0.0216
alpha1 0.1594 0.0397 4.0151 0.0001
beta1 0.8285 0.0426 19.4699 0.0000GARCH
El Modelo GARCH(r,s) es definido por:
\[X_t=\sqrt{h_t} \epsilon_t\] \[h_t= \alpha_0 + \sum_{i=1}^r \alpha_i X_{t-i}^2 + \sum_{j=1}^s \beta_j h_{t-j}\] \[= \alpha_0 +\alpha_1 X_{t-1}^2+\alpha_2 X_{t-2}^2+...+\alpha_r X_{t-r}^2\] \[+\beta_1 h_{t-1}+...+\beta_s h_{t-s}\] en donde \(\epsilon_t \sim i.i.d. N(0,1)\), \(\alpha_0 >0\), \(\alpha_i \geq 0\), \(\beta_j \geq 0\) y \(\sum\limits_{i=1}^q (\alpha_i+\beta_i) < 1, q=max(r,s)\).
Extensiones del modelo GARCH
- Exponential GAGRCH (EGARCH).
- Threshold GARCH (TGARCH).
- Integrated GARCH (IGARCH).
- …