Tema 9: Modelos lineales multivariados de series temporales
Paquetes de R
Para este tema, se necesita cargar estos paquetes:
Introducción
Contenido
Introducción
Medidas de dependencia (bivariada)
Medidas de dependencia (multivariada)
Estacionariedad
VAR(p)
Diagnósticos
ARMAX(p,q) vectorial
Introducción
En la práctica, es común enfrentar situaciones en donde se presentan varias series temporales.
Objetivos:
- Estudiar la relación dinámica de las variables de interés en el tiempo.
- Mejorar las predicciones.
Ejemplo 1: El Niño y la población de peces
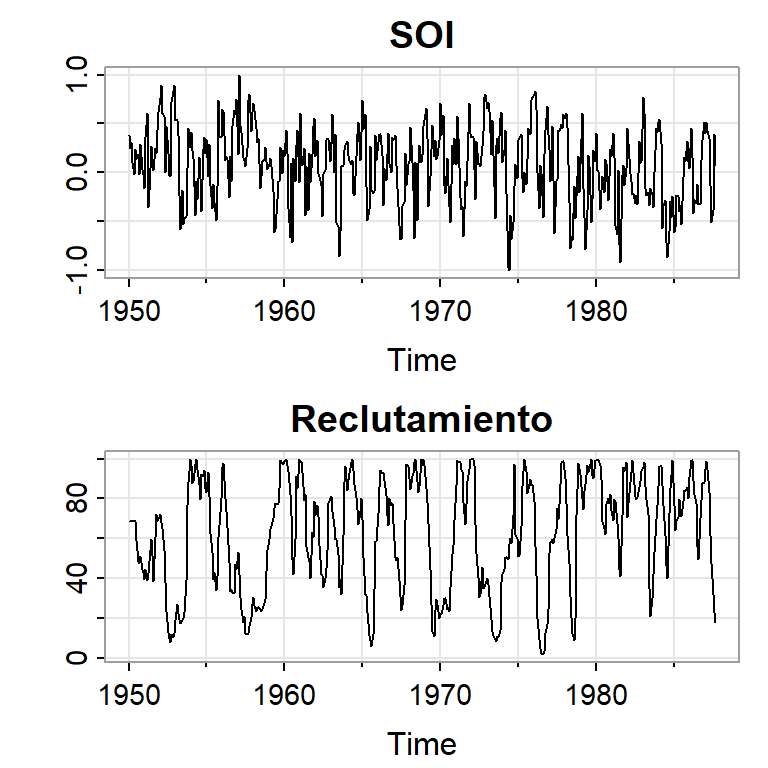
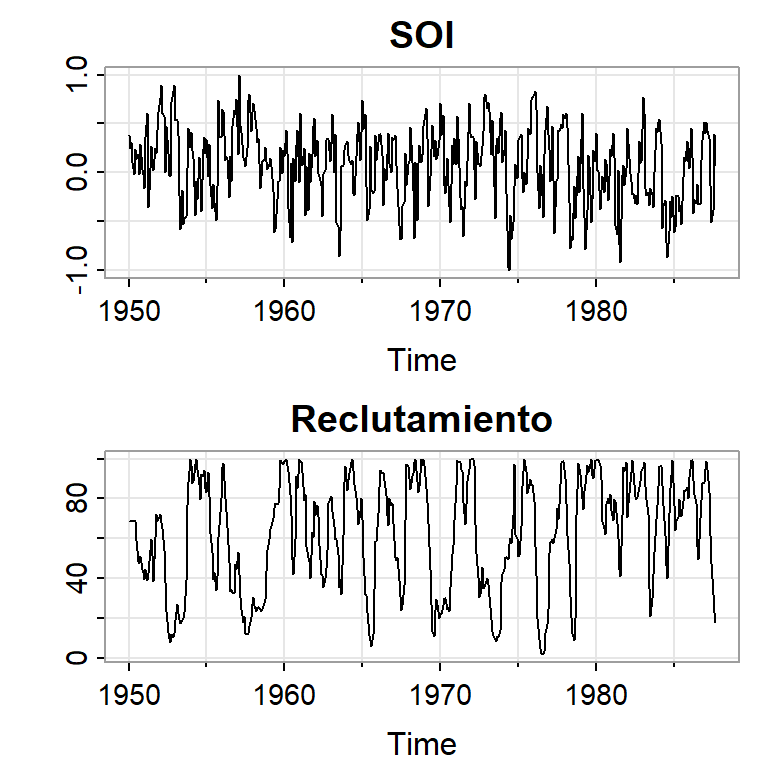
- Se tiene la serie ambiental de índice de oscilación del sur (SOI, Southern Oscillation Index), y la serie de número de peces nuevos (Reclutamiento) de 453 meses de 1950 a 1987.
- SOI mide cambios en presión relacionada a la temperatura del superficie del mar en el oceano pacífico central, el cual se calienta cada 3-7 años por el efecto El Niño.
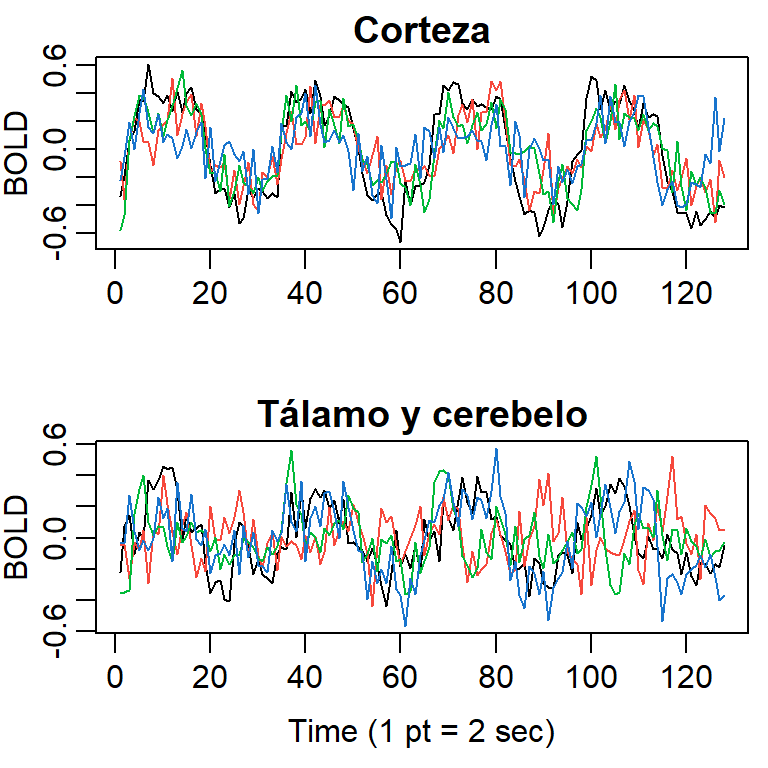
Ejemplo 2: Imagen por resonancia magnética
- Un estímulo fue aplicado a cinco personas en la mano por 32 segundos y luego paró el estímulo por otros 32 segundos, sucesivamente.
- Durante 256 segundos, cada 2 segundos se registró la intensidad del dependiente del nivel en la sangre (BOLD, blood oxygenation-level dependent signal intensity), la cual mide áreas de activación en el celebro \((T=128)\).
Medidas de dependencia (bivariada)
Contenido
Introducción
Medidas de dependencia (bivariada)
Medidas de dependencia (multivariada)
Estacionariedad
VAR(p)
Diagnósticos
ARMAX(p,q) vectorial
Medidas de dependencia (bivariada)
- Recuerde que la función de autocorrelación es definida por
\[\rho_X(t,s)=\frac{\gamma(t,s)}{\sqrt{\gamma(t,t)\gamma(s,s)}}\]
- Se puede generalizar estas medidas a dos series \(X_t\) y \(Y_t\). Defina la función de autocovariancia cruzada:
\[\gamma_{XY}(t,s)= Cov(X_t,Y_s) =E\left[ (X_t-\mu_{Xt})(Y_s-\mu_{Ys}) \right]\]
- la función de autocorrelación cruzada:
\[\rho_{XY}(t,s)= \frac{\gamma_{XY}(t,s)}{\sqrt{\gamma_{X}(t,t)\gamma_{Y}(s,s)}}\]
Definición 1 (Estacionariedad conjunta (bivariada)) Dos series temporales, \(X_t\) y \(Y_t\) se dicen que son conjuntamente estacionarias, si cada serie es estacionaria, y la función de covariancia cruzada
\[\gamma_{XY}(h)= Cov(X_{t+h},Y_t) =E\left[ (X_{t+h}-\mu_{X})(Y_t-\mu_{Y}) \right]\] es una función que solamente depende de \(h\).
De esta forma, podemos definir la función de correlación cruzada de dos series temporales conjuntamente estacionarias por \[\rho_{XY}(h)=\frac{\gamma_{XY}(h)}{\sqrt{\gamma_X(0),\gamma_Y(0)}}\]
Propiedades:
- \(-1 \leq \rho_{XY}(h) \leq 1\)
- \(\rho_{XY}(h) \neq \rho_{XY}(-h)\) pues \(Cov(X_2,Y_1)\) y \(Cov(X_1,Y_2)\) no siempre son iguales.
- \(\rho_{XY}(h) = \rho_{YX}(-h)\)
Estimación
- la función de autocovariancia cruzada muestral es definida por \[\hat{\gamma}_{XY}(h)=\frac{1}{T}\sum_{t=1}^{T-h} (X_{t+h}-\bar{X})(Y_{t}-\bar{Y}),\]
Note que \(\hat{\gamma}_{XY}(-h)=\hat{\gamma}_{YX}(h)\) para \(h=0,1,...,T-1\).
- La función de autocorrelación cruzada muestral es definida por \[\hat{\rho}_{XY}(h)=\frac{\hat{\gamma}_{XY}(h)}{\sqrt{\hat{\gamma}_X(0)\hat{\gamma}_Y(0)}}\] Propiedad: La distribución de \(\hat{\rho}_{XY}(h)\) para \(T\) grande es aproximadamente normal con media cero y \[\sigma_{\hat{\rho}_{XY}}=\frac{1}{\sqrt{T}}.\]
Ejemplo 1: El Niño y la población de peces
- Se tiene la serie ambiental de índice de oscilación del sur (SOI, Southern Oscillation Index), y la serie de número de peces nuevos (Reclutamiento) de 453 meses de 1950 a 1987.
- SOI mide cambios en presión relacionada a la temperatura del superficie del mar en el oceano pacífico central, el cual se calienta cada 3-7 años por el efecto El Niño.
[1] 0.60 0.37 0.21 0.05 -0.11 -0.19 -0.18 -0.10 0.05 0.22 0.36 0.41
[13] 0.31 0.10 -0.06 -0.17 -0.29 -0.37 -0.32 -0.19 -0.04 0.15 0.31 0.35
[25] 0.25 0.10 -0.03 -0.16 -0.28 -0.37 -0.32 -0.16 -0.02 0.17 0.33 0.39
[37] 0.30 0.16 0.00 -0.13 -0.24 -0.27 -0.25 -0.13 0.06 0.21 0.38 0.40 [1] 0.92 0.78 0.63 0.48 0.36 0.26 0.18 0.13 0.09 0.07 0.06 0.02
[13] -0.04 -0.12 -0.19 -0.24 -0.27 -0.27 -0.24 -0.19 -0.11 -0.03 0.03 0.06
[25] 0.06 0.02 -0.02 -0.06 -0.09 -0.12 -0.13 -0.11 -0.05 0.02 0.08 0.12
[37] 0.10 0.06 0.01 -0.02 -0.03 -0.03 -0.02 0.01 0.06 0.12 0.17 0.20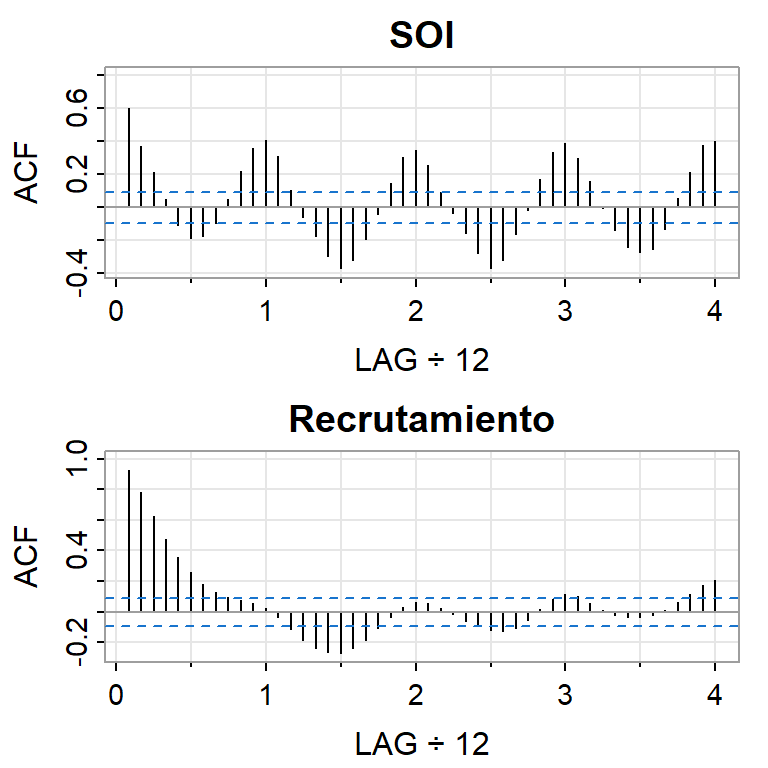
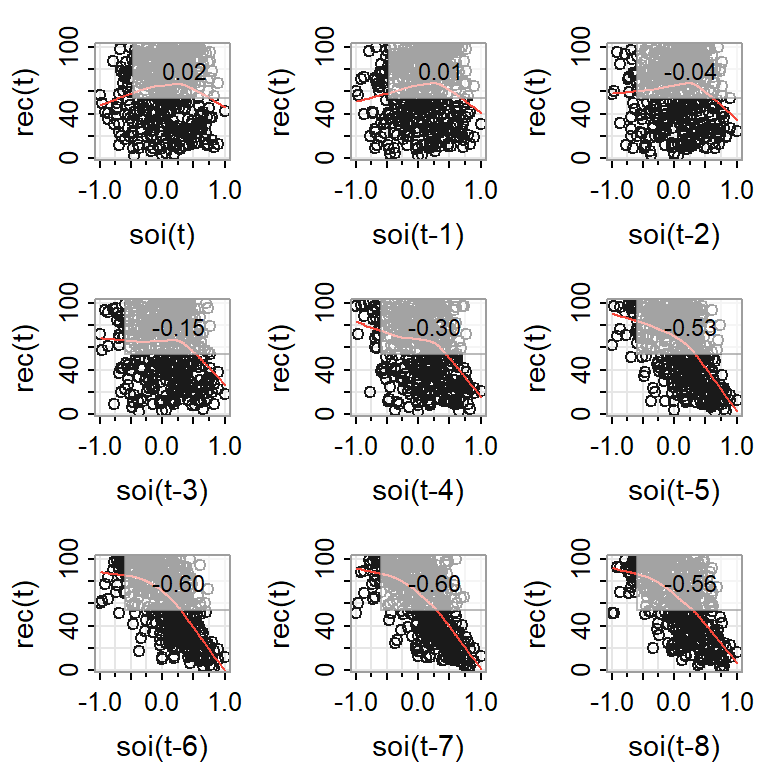
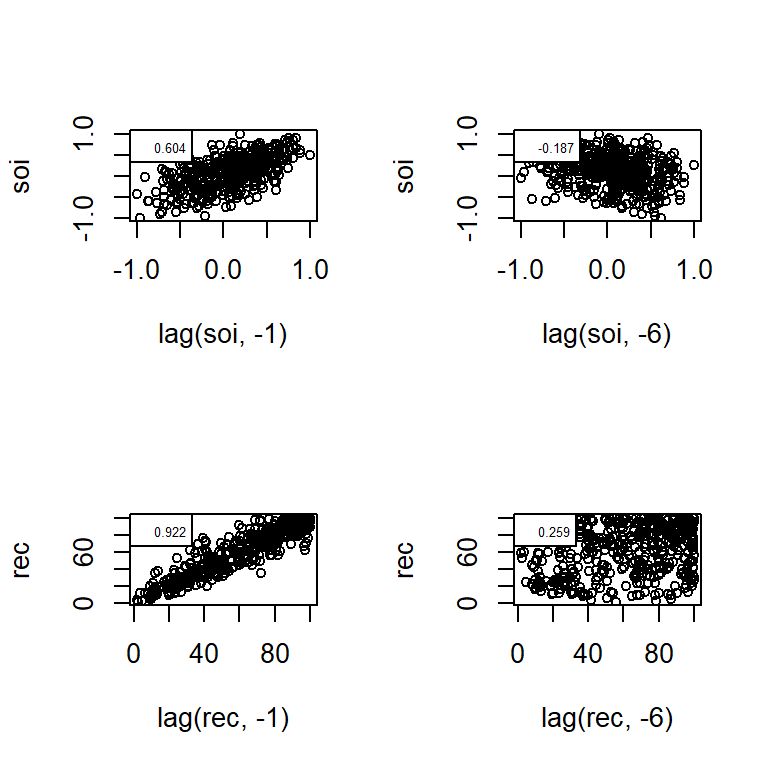
Gráfico de dispersión de REC contra SOI rezagadas
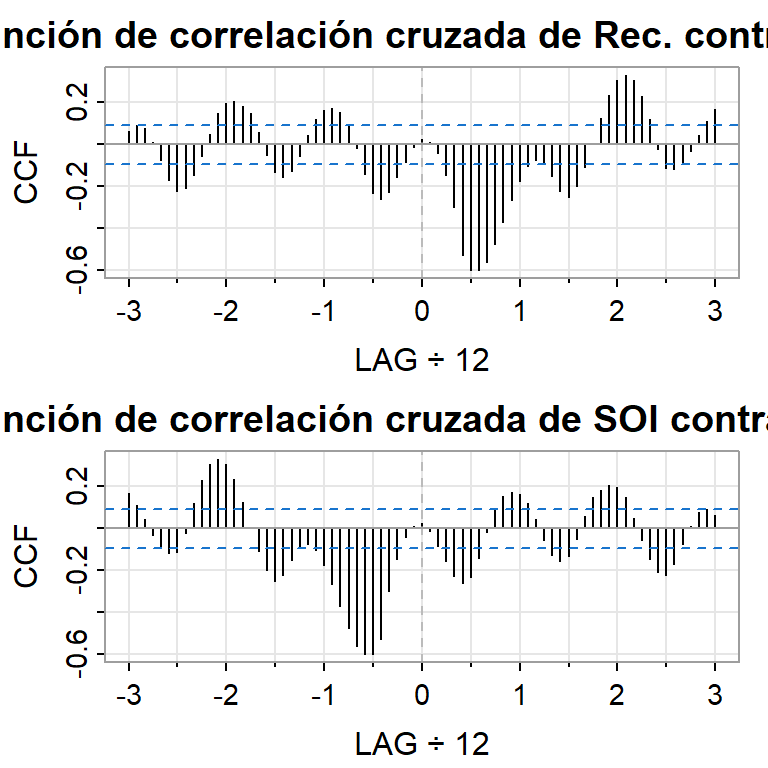
Autocorrelations of series 'X', by lag
-0.4167 -0.3333 -0.2500 -0.1667 -0.0833 0.0000 0.0833 0.1667 0.2500 0.3333
-0.259 -0.228 -0.154 -0.086 -0.013 0.025 0.011 -0.042 -0.146 -0.297
0.4167
-0.527
Autocorrelations of series 'X', by lag
-0.4167 -0.3333 -0.2500 -0.1667 -0.0833 0.0000 0.0833 0.1667 0.2500 0.3333
-0.527 -0.297 -0.146 -0.042 0.011 0.025 -0.013 -0.086 -0.154 -0.228
0.4167
-0.259 - Note que \(\hat{\rho}_{XY}(h) = \hat{\rho}_{YX}(-h)\).
Medidas de dependencia (multivariada)
Contenido
Introducción
Medidas de dependencia (bivariada)
Medidas de dependencia (multivariada)
Estacionariedad
VAR(p)
Diagnósticos
ARMAX(p,q) vectorial
Medidas de dependencia (multivariada)
La generalización a series temporales multivariadas con \(k\) componentes, \(X_{t1},...X_{tk}, t=1,...,T\), es intuitivo:
El vector de medias es función del tiempo \(t\): \[\mu_t=E(X_t)=\left(\begin{array}{c} \mu_{t1}\\ \vdots \\ \mu_{tk} \end{array}\right).\]
La función de autocovariancia cruzada:
\[\gamma_{ij}(t,s)= Cov(X_{ti},X_{sj}) =E\left[ (X_{ti}-\mu_{ti})(X_{sj}-\mu_{sj}) \right]\] para \(i,j=1,...,k.\)
- O bien, la matriz de autocovariancias: \[\Gamma(t,s)= E[(X_{t}-\mu_{t})(X_{s}-\mu_s)']=E\left[ \left( \begin{array}{c} X_{t1}-\mu_{t1}\\\vdots \\X_{tk}-\mu_{tk} \end{array} \right) \left( X_{s1}-\mu_{s1},\dots ,X_{sk}-\mu_{sk} \right) \right]\]
\[= E\left( \begin{array}{c} (X_{t1}-\mu_{t1})(X_{s1}-\mu_{s1}) & \dots & (X_{t1}-\mu_{t1})(X_{sk}-\mu_{sk})\\ \vdots & \ddots & \vdots \\(X_{tk}-\mu_{tk})(X_{s1}-\mu_{s1}) & \dots & (X_{tk}-\mu_{tk})(X_{sk}-\mu_{sk}) \end{array} \right).\]
Estacionariedad
Contenido
Introducción
Medidas de dependencia (bivariada)
Medidas de dependencia (multivariada)
Estacionariedad
VAR(p)
Diagnósticos
ARMAX(p,q) vectorial
Estacionariedad débil
Definición 2 (Estacionariedad débil) Sea \(X_t=(X_{t1},...,X_{tk})'\) un vector \(k \times 1\) de series temporales. Se dice que \(X_t\) es débilmente estacionario si:
El vector de medias es constante en el tiempo \[\mu=E(X_t)=\left(\begin{array}{c} \mu_1\\ \vdots \\ \mu_k \end{array}\right)\]
Y la matriz de autocovariancia depende únicamente del rezago \(h\), i.e. \[\Gamma(h)= E[(X_{t+h}-\mu)(X_{t}-\mu)']\] donde los elementos de la matriz son funciones de covariancia cruzada, \(\gamma_{ij}(h)= Cov(X_{t+h,i},X_{t,j}) =E\left[ (X_{t+h,i}-\mu_{i})(X_{tj}-\mu_{j}) \right]\) para \(i,j=1,...,k\).
- Note que como \(\gamma_{ij}(h)=\gamma_{ji}(-h)\), entonces
\[\Gamma(-h)=\Gamma'(h)\]
la matriz de autocorrelaciones también depende únicamente del rezago \(h\), i.e. \[\boldsymbol{\rho}(h)= D^{-1}\Gamma(h) D^{-1}=\left[ \rho_{h,ij} \right]\] donde \(D=diag\left\lbrace \sigma_1,...,\sigma_k \right\rbrace\) es la matriz diagonal de desviaciones estándares de los componentes de \(X_t\).
Al igual que \(\Gamma(h)\), se tiene que \[\boldsymbol{\rho}(-h)=\boldsymbol{\rho}'(h)\]
Estacionariedad estricta
Definición 3 (Estacionariedad estricta) Sea \(X_t=(X_{t1},...,X_{tk})'\) un vector \(k \times 1\) de series temporales. Se dice que \(X_t\) es estrictamente estacionario, si la distribución conjunta multivariada de una colección de m tiempos: \[\left\lbrace X_{t_1},...,X_{t_m} \right\rbrace\] es igual a \[\left\lbrace X_{t_1+h},...,X_{t_m+h} \right\rbrace\] donde \(m,j\) y \(t_1,...,t_m\) son enteros positivos arbitrarios.
Nota
- Una serie temporal estrictamente estacionaria es débilmente estacionaria, si sus primeros dos momentos existen.
Ruido blanco
Definición 4 (Ruido blanco)
Es una colección de vectores de variables aleatorias no correlacionadas, \(a_t\), con media \(0\) y matriz de covariancias \(\Sigma_a\).
Denotado por \(a_t \sim wn(0,\Sigma_a)\).
Si una secuencia de variables es i.i.d., i.e. \(a_t \sim iid(0,\Sigma_a)\), entonces \(a_t \sim wn(0,\Sigma_a)\).
Sin embargo, si un ruido blanco es Gaussiano, entonces \(a_t \overset{iid}{\sim} N(0,\Sigma_a)\).
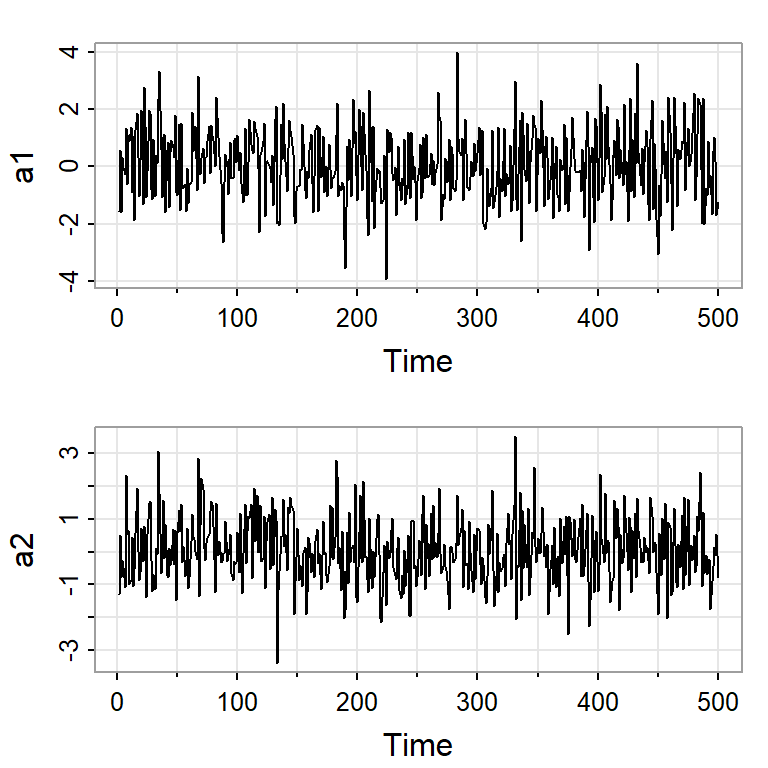
Considere un ruido blanco Gaussiano: \[a_t \sim N\left( \left( \begin{array}{c} 0\\ 0 \end{array}\right) , \begin{bmatrix}1.5 & 0.8 \\ 0.8 & 1 \end{bmatrix} \right).\]
Note que su función de autocovariancia es \[\Gamma(h)=\left\lbrace \begin{aligned} \begin{bmatrix}1.5 & 0.8 \\ 0.8 & 1 \end{bmatrix} & & h = 0, \\ 0, & & h \neq 0. \end{aligned} \right.\]
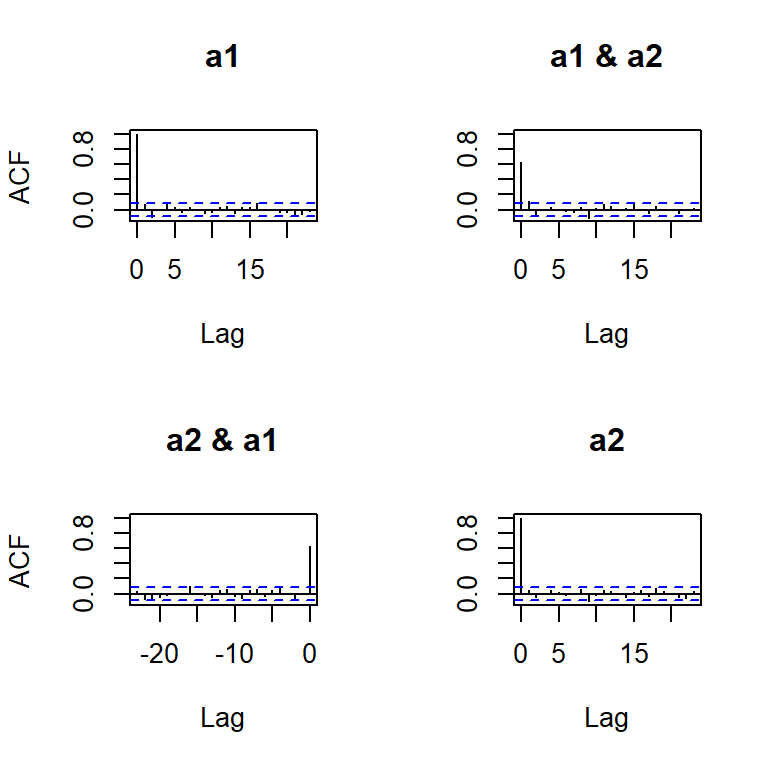
VAR(p)
Contenido
Introducción
Medidas de dependencia (bivariada)
Medidas de dependencia (multivariada)
Estacionariedad
VAR(p)
Diagnósticos
ARMAX(p,q) vectorial
VAR(p)
Es un caso particular de los modelos de series temporales multivariados que supone que la observación de cada variable depende linealmente de los rezagos pasados de ella misma y también de otras variables.
Comúnmente se les conoce como modelos autorregresivos multivariados o modelos autorregresivos vectoriales.
Empezamos con el modelo autorregresivo vectorial de orden 1, VAR(1), de dimensión 3 (3 series): \(X_{t,1},X_{t,2},X_{t,3}\).
El VAR(1) se define de la siguiente forma:
\[\begin{align*} X_{t,1} &= \alpha_1 + \Phi_{11} X_{t-1,1} + \Phi_{12} X_{t-1,2} + \Phi_{13} X_{t-1,3} + w_{t,1}, \\ X_{t,2} &= \alpha_2 + \Phi_{21} X_{t-1,1} + \Phi_{22} X_{t-1,2} + \Phi_{23} X_{t-1,3} + w_{t,2}, \\ X_{t,3} &= \alpha_3 + \Phi_{31} X_{t-1,1} + \Phi_{32} X_{t-1,2} + \Phi_{33} X_{t-1,3} + w_{t,3}. \end{align*}\]
- Note que cada ecuación establece un modelo autorregresivo de orden 1 más otras variables de un rezago.
VAR(1)
- En concreto, el modelo anterior se puede resumir en
\[\boldsymbol{X}_{t}=\boldsymbol{\alpha}+\boldsymbol{\Phi}\boldsymbol{X}_{t-1}+\boldsymbol{w}_{t}\] en donde
\[\boldsymbol{X}_{t}= \begin{bmatrix}x_{t,1}\\ x_{t,2}\\ x_{t,3} \end{bmatrix}~~~~~ \boldsymbol{\alpha}= \begin{bmatrix}\alpha_{1}\\ \alpha_{2}\\ \alpha_{3} \end{bmatrix}~~~~~ \boldsymbol{\Phi}=\begin{bmatrix}\Phi_{11} & \Phi_{12} & \Phi_{13} \\ \Phi_{21} & \Phi_{22} & \Phi_{23}\\ \Phi_{31} & \Phi_{32} & \Phi_{33} \end{bmatrix}~~~~~ \boldsymbol{w}_{t}= \begin{bmatrix}w_{t,1}\\ w_{t,2}\\ w_{t,3} \end{bmatrix}\]
VARX(1)
- También es posible extender el modelo anterior con intercepto y tendencia: \[\boldsymbol{X}_{t}=\boldsymbol{\Gamma} \boldsymbol{u}_t+\boldsymbol{\Phi}\boldsymbol{X}_{t-1}+\boldsymbol{w}_{t},\]
\[\text{donde}~~ \boldsymbol{\Gamma}=\begin{bmatrix}\alpha_{1} & \beta_{1} \\ \alpha_{2} & \beta_{2} \\ \alpha_{3} & \beta_{3} \end{bmatrix} ~~\text{y}~~ \boldsymbol{u}_t= \begin{bmatrix}1 \\ t \end{bmatrix}\]
Es decir, \[\begin{align*} X_{t,1} &= \alpha_1 + \beta_1 t + \Phi_{11} X_{t-1,1} + \Phi_{12} X_{t-1,2} + \Phi_{13} X_{t-1,3} + w_{t,1}, \\ X_{t,2} &= \alpha_2 + \beta_2 t + \Phi_{21} X_{t-1,1} + \Phi_{22} X_{t-1,2} + \Phi_{23} X_{t-1,3} + w_{t,2}, \\ X_{t,3} &= \alpha_3 + \beta_3 t + \Phi_{31} X_{t-1,1} + \Phi_{32} X_{t-1,2} + \Phi_{33} X_{t-1,3} + w_{t,3}. \end{align*}\]
Note que X en ARX se refiere al vector exógeno denotado por \(u_t\) y se puede extender fácilmente incluyendo variable exógenas.
VARX(p)
- De esta forma, se puede generalizar a series temporales \(K\)-dimensionales y \(p\) rezagos:
\[\boldsymbol{X}_{t}=\boldsymbol{\Gamma} \boldsymbol{u}_t+\boldsymbol{\Phi_1}\boldsymbol{X}_{t-1}+...+\boldsymbol{\Phi_p}\boldsymbol{X}_{t-p}+\boldsymbol{w}_{t}\] en donde \(u_t\) es un vector \(k \times 1\) de \(k\) variables exógenas y \(\boldsymbol{\Gamma}\) es una matriz \(r \times k\) de coeficientes asociados a las variables exógenas, y
\[\boldsymbol{X}_{t}= \begin{bmatrix}X_{t,1}\\ \vdots \\ X_{t,K} \end{bmatrix},~~~\boldsymbol{\Phi}_i=\begin{bmatrix}\Phi_{i,1,1} & \dots & \Phi_{i,1,K} \\ \vdots & \ddots & \vdots\\ \Phi_{i,K,1} & \dots & \Phi_{i,K,v} \end{bmatrix}~~~~~,i=1,...,p, ~~\text{y}~~~~~\] \[\boldsymbol{w}_{t}= \begin{bmatrix}w_{t,1}\\ \vdots\\ w_{t,K} \end{bmatrix}\]
ARX(p) multivariado o VARX(p)
- Considere el modelo en término del polinomio de rezagos:
\[A(B) \boldsymbol{X}_{t}=\boldsymbol{\Gamma} \boldsymbol{u}_t+\boldsymbol{w}_{t}\] donde \(A(B)=I-\boldsymbol{\Phi_1}B-...-\boldsymbol{\Phi_p}B^{p}\) es el polinomio autoregresivo
- El modelo VARX(p) es estacionario (estable) si
\[\det(I-\boldsymbol{\Phi_1}z-...-\boldsymbol{\Phi_p}z^{p}) \neq 0 ~~\text{para }|z|\leq 1.\]
- En la práctica, se utiliza el hecho de que cualquier VAR(p) se puede representar como un VAR(1) por medio de la matriz compañera A:
\[\boldsymbol{\xi}_{t}=A\boldsymbol{\xi}_{t-1}+\boldsymbol{v}_{t}\] donde \[\boldsymbol{\xi}_{t (Kp)}= \begin{bmatrix}X_{t}\\ \vdots \\ X_{t-p+1} \end{bmatrix},~~~A=\begin{bmatrix}\Phi_{1} & \Phi_2 & ... & \Phi_{p-1} & \Phi_{p} \\ I & 0 & ... & 0 & 0 \\ 0 & I & ... & 0 & 0\\ \vdots & \vdots & \ddots & \vdots & \vdots \\ 0 & 0 & ... & I & 0 \end{bmatrix}~,~ \boldsymbol{v}_{t}= \begin{bmatrix}w_{t}\\ 0 \\ \vdots\\ 0 \end{bmatrix}\] y \(\boldsymbol{\xi}_{t}\) y \(\boldsymbol{v}_{t}\) son vectores \(Kp \times 1\), y \(A\) es una matriz \(Kp \times Kp\).
- Luego, la condición anterior de estacionariedad es equivalente a que todos los eigenvalues de la matriz \(A\) tienen módulo menor a 1.
Criterio de información
Debido a la complejidad de selección del orden \(p\), en la práctica se usan los criterios de información:
- AIC: \[AIC(p)= \log \det(\tilde{Z}_u(p))+\frac{2}{T}pK^2\]
- HQ (Hannan-Quinn): \[HQ(p)= \log \det(\tilde{Z}_u(p))+\frac{2\log(\log(T))}{T}pK^2\] donde \(\tilde{Z}_u(p)=T^{-1}\sum_{t=1}^T \hat{w}_t \hat{w}'_t\),
\(p^*\) es el total de parámetros en cada ecuación y
\(p\) es el orden de rezago.
- BIC o criterio de información de Schwarz (SC): \[SC(p)= \log \det(\tilde{Z}_u(p))+\frac{\log(T)}{T}pK^2\]
- FPE (Final Predictor Error): \[FPE(p)=\left( \frac{T+p^*}{T-p^*}\right)^K \det(\tilde{Z}_u(p))\]
Diagnósticos
Contenido
Introducción
Medidas de dependencia (bivariada)
Medidas de dependencia (multivariada)
Estacionariedad
VAR(p)
Diagnósticos
ARMAX(p,q) vectorial
Diagnósticos
Pruebas de hipótesis para la correlación serial:
El estadístico de Portmanteau: \[Q_h=T \sum_{j=1}^h tr(\hat{C}'_j\hat{C}^{-1}_0\hat{C}_j\hat{C}^{-1}_0)\] donde \(\hat{C}_i=\frac{1}{T}\sum_{j=i+1}^T \hat{w}_t\hat{w}'_{t-i}\). Para \(T\) y \(h\) suficientemente grandes, el estadístico se aproxima a la distribución \(\chi^2(K^2(h-n^*))\), donde \(n^*\) es la cantidad de parámetros excluyendo los de términos determinísticos.
El estadístico de Portmanteau ajustado (muestras pequeñas): \[Q^*_h=T^2 \sum_{j=1}^h \frac{1}{T-j} tr(\hat{C}'_j\hat{C}^{-1}_0\hat{C}_j\hat{C}^{-1}_0)\]
Ejemplo
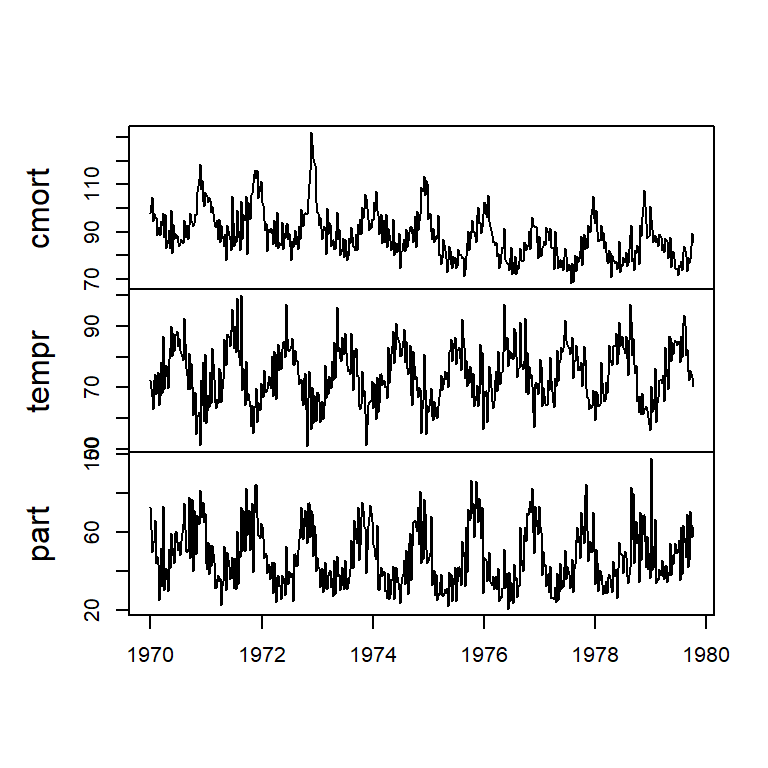
- 3 series semanales en la zona rural de Los Angeles, EU de 1970 a 1980 \((T=508)\).
- promedio semanal de mortalidad cardiovascular.
- temperatura (F)
- nivel de partícula (contaminación)
ARMAX(p,q) vectorial
Contenido
Introducción
Medidas de dependencia (bivariada)
Medidas de dependencia (multivariada)
Estacionariedad
VAR(p)
Diagnósticos
ARMAX(p,q) vectorial
ARMAX(p,q) vectorial
- El modelo ARMAX(p,q) \(r\)-dimensionales:
\[\boldsymbol{X}_{t}=\boldsymbol{\Gamma} \boldsymbol{u}_t+ \sum_{i=1}^p \boldsymbol{\Phi_i}\boldsymbol{X}_{t-i} - \sum_{j=1}^q \boldsymbol{\Theta_j}\boldsymbol{w}_{t-j} +\boldsymbol{w}_{t}\] con \(\boldsymbol{\Phi_p}, \boldsymbol{\Theta_q} \neq \boldsymbol{0}\) y \(\Sigma_\boldsymbol{w}\) definida positiva.
- Los coeficientes \(\boldsymbol{\Phi_i}:i=1,...,p\), \(\boldsymbol{\Theta_j}:j=1,...,q\) son matrices \(r \times r\)
VARMA(p,q)
Para el caso del VARMA(p,q), i.e. tiene media cero, el modelo se especifica de la forma
\[\boldsymbol{\Phi}(B) \boldsymbol{X}_{t}= \boldsymbol{\Theta}(B) \boldsymbol{w}_{t}\] en donde
\(\boldsymbol{\Phi}(B)=I- \boldsymbol{\Phi}_1 B-...- \boldsymbol{\Phi}_p B^p\) es el operador autorregresivo y
\(\boldsymbol{\Theta}(B)=I- \boldsymbol{\Theta}_1 B-...- \boldsymbol{\Theta}_q B^q\) es el operador de medias móviles.
- El modelo se dice que es causal (estacionario) si las raíces de \(|\boldsymbol{\Phi}(B)|\), están fuera del círculo unitario.
- El modelo se dice que es invertible si las raíces de \(|\boldsymbol{\Theta}(B)|\), están fuera del círculo unitario.
Temas adicionales
- ARFIMA o FARIMA o ARIMA fraccional.
- Series temporales con memoria larga.
- Otras extensiones de ARCH-GARCH.
- Procesos localmente estacionarios.
- Procesos cointegrados.
- Modelos de espacio de estados.
- Análisis espectral (dominio de frecuencia).
- y otros.