Tema 2: Descomposición de series temporales
Paquetes de R
Para este tema, se necesita cargar estos paquetes:
Componentes de las series temporales
Contenido
Componentes de las series temporales
Medias móviles
Descomposición aditiva
Descomposición multiplicativa
Otras técnicas de descomposición
Descomposición STL
Descomposición y pronóstico
Componentes de las series temporales
Existe varios componentes en el comportamiento de series temporales.
Tendencia: comportamiento creciente o decreciente en largo plazo. Ej: crecimiento de población, ingresos por ventas.
Estacionalidad: patrón o variaciones afectadas por repetición de una frecuencia dada (ej. semana, mes y año.). Consecuencia de cambios climáticos, comportamiento de la gente en el tiempo. Ej: venta de productos que dependen de la temporada, temperatura, pasajes de avión.
Ciclo: cuando los datos muestran subidas y bajadas de largo plazo, generalmente con frecuencia desconocida. Ej: ciclo económico, período de prosperidad alternando con período de recesión.
Movimiento irregular o error: variaciones en la serie que no siguen ningún patrón regular. Es el residuo que queda en una serie después de eliminar los componentes anteriores (tendencia-ciclo y estacionalidad).
Descomposición de series temporales
- Surgió al inicio del siglo XX.
- Los métodos más antiguos para describir y analizar series cronológicas.
- Los objetivos de esta metodología consisten en:
- Eliminar el componente de tendencia en una serie con el fin de estudiar la correlación serial entre las observaciones de la serie.
- Separar los componentes para describir los diferentes componentes.
- Generalmente combinamos el componente de tendencia con el de ciclo, llamado tendencia-ciclo (o simplemente tendencia).
- Veremos métodos que consisten en descomponer una serie en:
- tendencia-ciclo,
- estacionalidad y
- el componente irregular.
Descomposición Clásica
- Modelo aditivo
\[Z_{t} = T_{t} + S_{t} + I_t,\]
- Modelo multiplicativo
\[Z_{t} = T_{t} \times S_{t} \times I_t,\] donde:
\(Z_t\): el valor de la serie \(Z\) en el tiempo \(t\),
\(T_t\): componente tendencia-ciclo en el tiempo \(t\).
\(S_t\): componente estacional en el tiempo \(t\).
\(I_t\): componente irregular, aleatorio en el tiempo \(t\).
Nota
La descomposicion aditiva es la más apropiada si la magnitud de las fluctuaciones o la variación alrededor del tendencia-ciclo no varía con el nivel de la serie de tiempo.
La descomposición multiplicativa se usa cuando la variación en el patrón estacional o la variación alrededor de tendencia-ciclo, parece ser proporcional al nivel de la serie de tiempo. Es común ver esto en las series del ámbito económico.
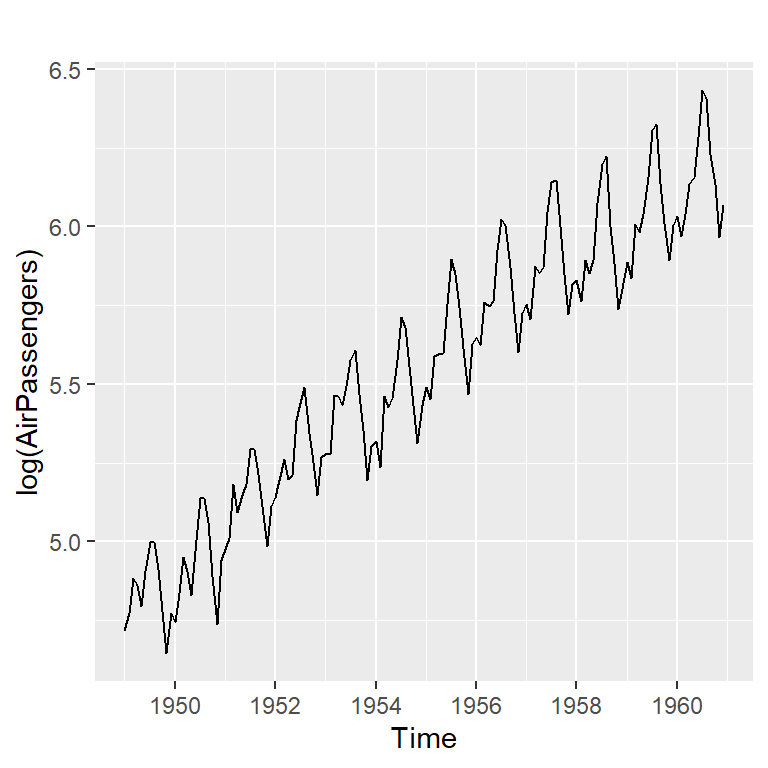
Utilizando la transformación logarítmica en una serie de datos, el modelo multiplicativo se convierte en un modelo aditivo. (Esto equivale a estabilizar la variabilidad a lo largo del tiempo) \[Z_t=T_t \times S_t \times I_t\] es equivalente a \[\log Z_t = \log T_t + \log S_t + \log I_t.\]
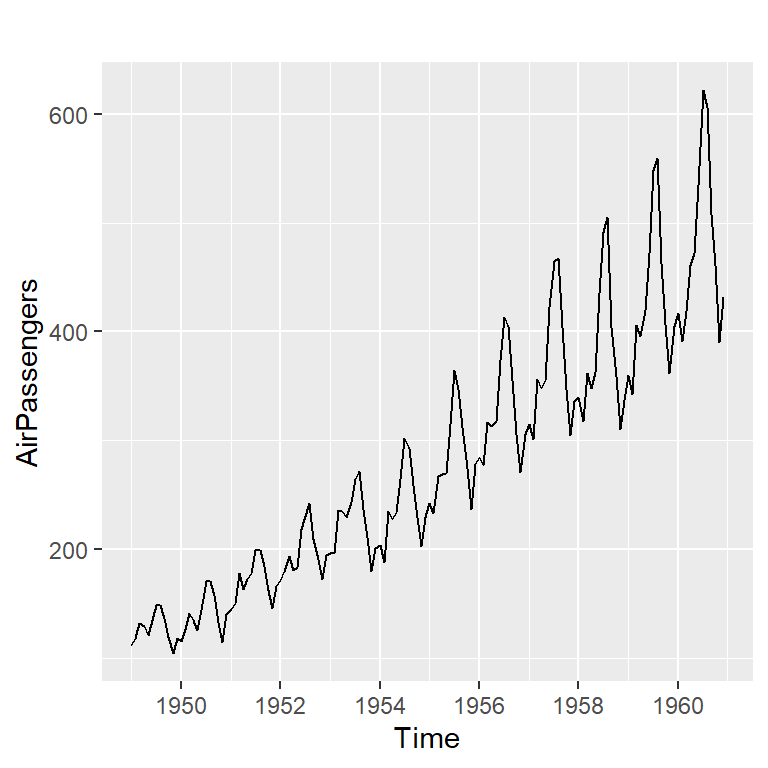
Ejemplo de los Pasajeros mensuales
- Recordemos del ejemplo de pasajeros mensuales.
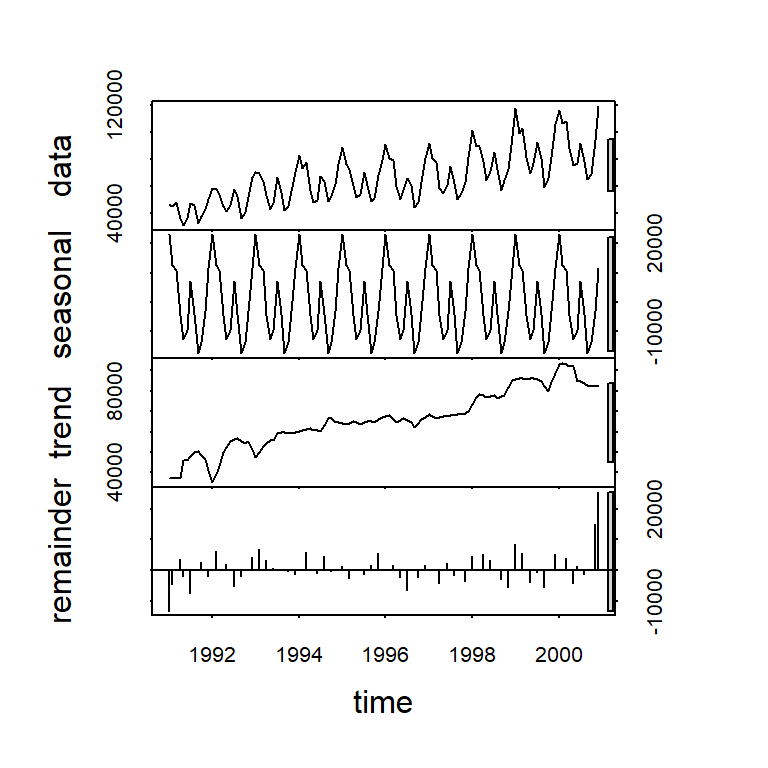
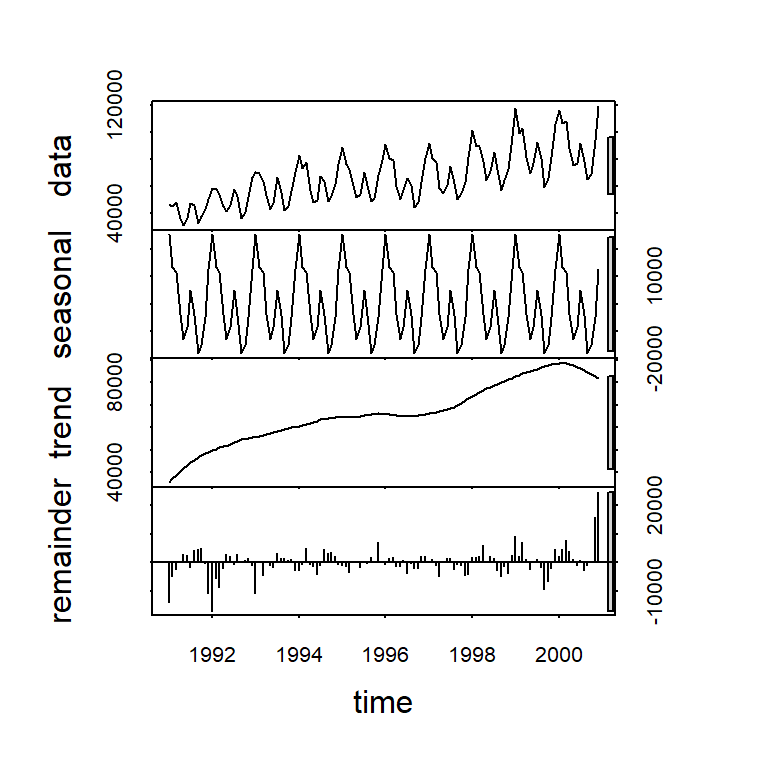
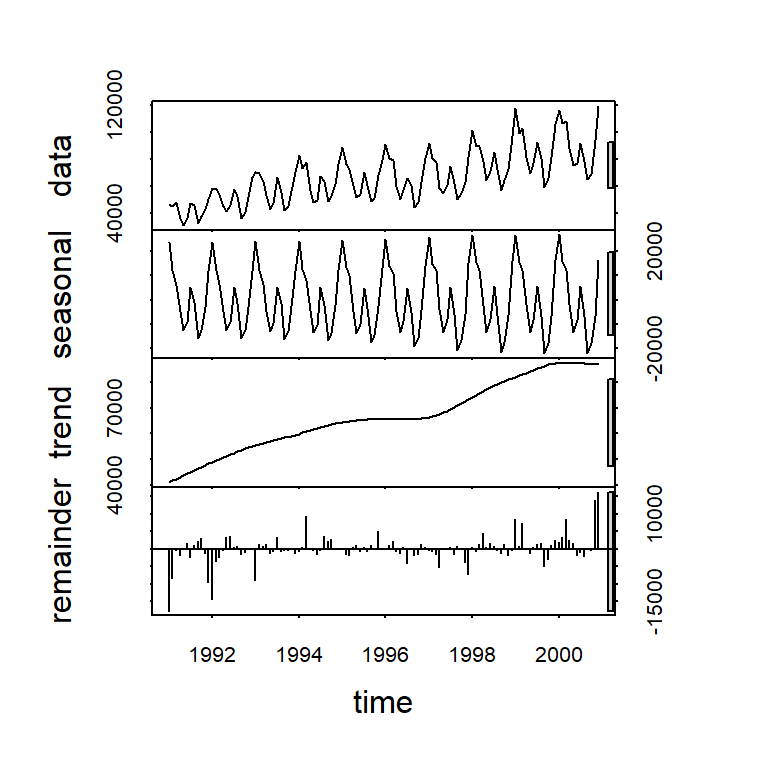
- La descomposición consiste en descomponer la serie en diferentes componentes.
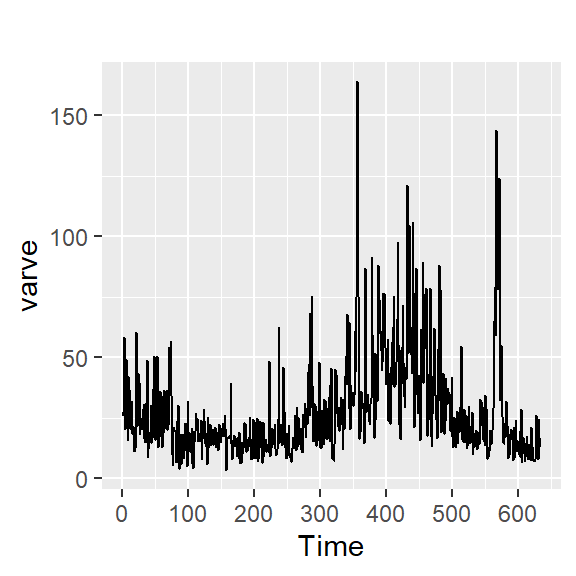
Ejemplo de serie anual de Varva glacial
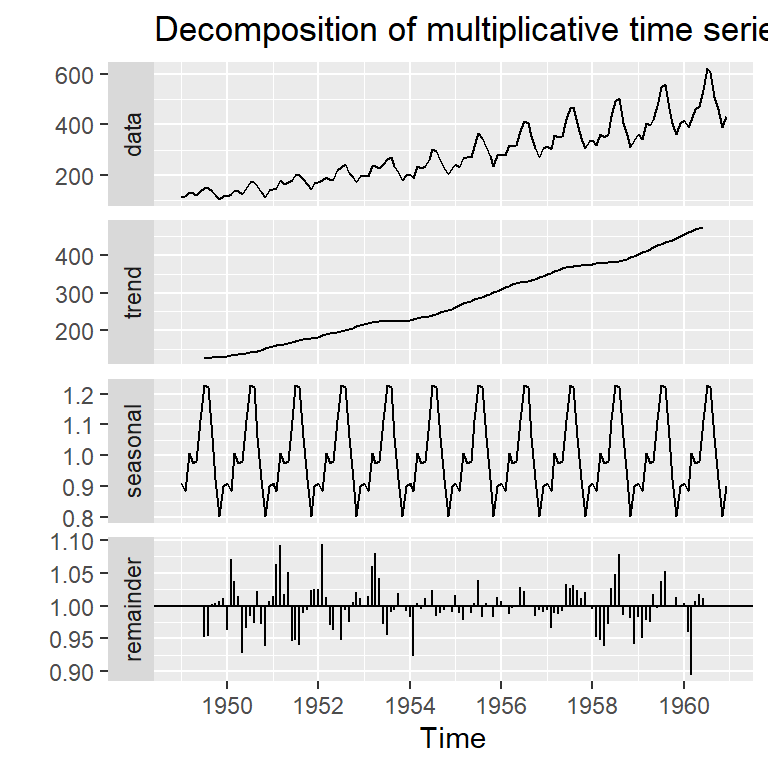
Los glaciares que se derriten depositan capas anuales de arena y limo durante las temporadas de derretimiento de primavera, que pueden reconstruirse anualmente durante un período que va desde el momento en que comenzó la desglaciación en Nueva Inglaterra (hace unos 12.600 años) hasta el momento en que terminó (hace unos 6000 años). Dichos depósitos sedimentarios, llamados varvas, pueden utilizarse como sustitutos de parámetros paleoclimáticos, como la temperatura, porque, en un año cálido, se depositan más arena y limo del glaciar en retroceso.
Note que la variabilidad es proporcional al nivel de la serie y no al tiempo.
Medias móviles
Contenido
Componentes de las series temporales
Medias móviles
Descomposición aditiva
Descomposición multiplicativa
Otras técnicas de descomposición
Descomposición STL
Descomposición y pronóstico
Medias móviles
El primer paso en una descomposición clásica es utilizar un método de media móvil para estimar el ciclo de tendencia.
Sea \(Z_t\) una serie de interés. Una media móvil de orden \(m\) se puede escribir como: \[\begin{equation} MA_{t} = \frac{1}{m} \sum_{j=-k}^k Z_{t+j}, \end{equation}\] donde \(m = 2k+1\) es impar1.
La estimación de tendencia-ciclo en el momento \(t\) se obtiene promediando los valores de la serie temporal dentro de \(k\) períodos de \(t\).
El promedio elimina parte de la aleatoriedad de los datos, dejando un componente tendencia-ciclo uniforme, es decir suaviza la serie original. A esto se le llama \(m\)-MA, que significa media móvil de orden \(m\).
AirPassengers ma(AirPassengers, 3) ma(AirPassengers, 5)
Jan 1949 112 NA NA
Feb 1949 118 120.6667 NA
Mar 1949 132 126.3333 122.4
Apr 1949 129 127.3333 127.0
May 1949 121 128.3333 133.0
Jun 1949 135 134.6667 136.2
Jul 1949 148 143.6667 137.6
Aug 1949 148 144.0000 137.2
Sep 1949 136 134.3333 131.0
Oct 1949 119 119.6667 125.0 AirPassengers ma(AirPassengers, 3) ma(AirPassengers, 5)
Mar 1960 419 423.6667 432.0
Apr 1960 461 450.6667 455.6
May 1960 472 489.3333 501.8
Jun 1960 535 543.0000 539.2
Jul 1960 622 587.6667 548.6
Aug 1960 606 578.6667 546.4
Sep 1960 508 525.0000 517.4
Oct 1960 461 453.0000 479.4
Nov 1960 390 427.6667 NA
Dec 1960 432 NA NA
Figura 5: Diferentes medias móviles aplicado a los datos de pasajeros
Descomposición aditiva
Contenido
Componentes de las series temporales
Medias móviles
Descomposición aditiva
Descomposición multiplicativa
Otras técnicas de descomposición
Descomposición STL
Descomposición y pronóstico
Descomposición aditiva
- Suponemos que el período estacional \(m\) es conocido. Ej: \(m=4\) para datos trimestrales, \(m=12\) para datos mensuales, \(m=7\) para datos diarios por semana, etc.
Paso I:
- Si \(m\) es impar, se calcula \(m\)-MA de la siguiente forma: \[MA_t=\frac{Z_{t-\frac{(m-1)}{2}}+...+Z_{t}+...+Z_{t+\frac{(m-1)}{2}}}{m}\]
- Si \(m\) es par, se debe calcular primero \(m\)-MA correspondiente al periodo \(t-\frac{1}{2}\): \[MA_{1t}=\frac{Z_{t-\frac{m}{2}}+...+Z_{t}+...+Z_{t+\frac{m}{2}-1}}{m}\]
Luego se calcula la \(m\)-MA correspondiente al periodo \(t+\frac{1}{2}\): \[MA_{2t}=\frac{Z_{t-\frac{m}{2}+1}+...+Z_{t}+...+Z_{t+\frac{m}{2}}}{m}\]
Se calcula una media móvil centrada de la siguiente forma: \[MA_t=\frac{MA_{1t}+PM_{2t}}{2}.\]
- \(MA_t\) es la estimación del componente tendencia-ciclo \(T_t\).
Paso II: Calcule \(R_t=Z_t -MA_t\) que es una estimación del componente estacional más el componente irregular, i.e. \(S_t+I_t\).
Paso III: Para estimar el componente estacional, agrupar los valores \(R_t\), correspondientes a cada estación \(m\) y calcular un promedio para cada estación. De esta forma, obtenemos los índices estacionales: \[S^*_j,~~~j=1,...m.\] Se debe ajustar estos índices para que sumen 0, y así se obtienen los índices estacionales normalizados. \[S_j=S^*_j-\bar{S^*}\] Se interpreta que la serie \(Z_t\) es \(S_j\) mayor (o menor) que la serie ajustada en el periodo \(j\).
Paso IV:
Se obtiene la serie ajustada estacionalmente, que son los valores desestacionalizados usando \(d_t=Z_t-S_j\).
Paso V:
Finalmente, se obtiene el residuo \(I_t=Z_t-T_t-S_j\).
Ejemplo 2.1 de Hernández (2011): Serie de número de contrayentes en los matrimonios celebrados en Costa Rica de 1978 a 1983.
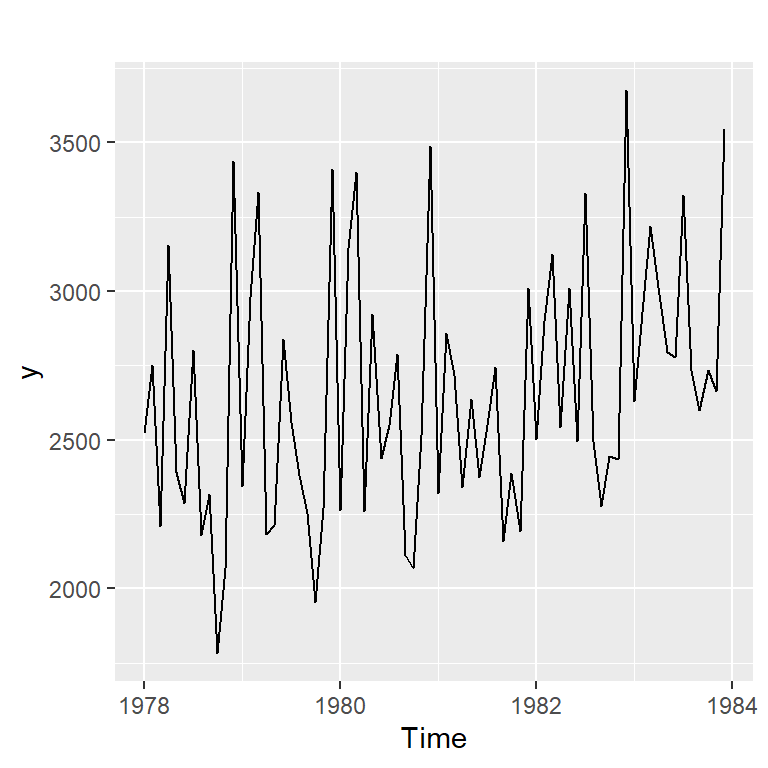
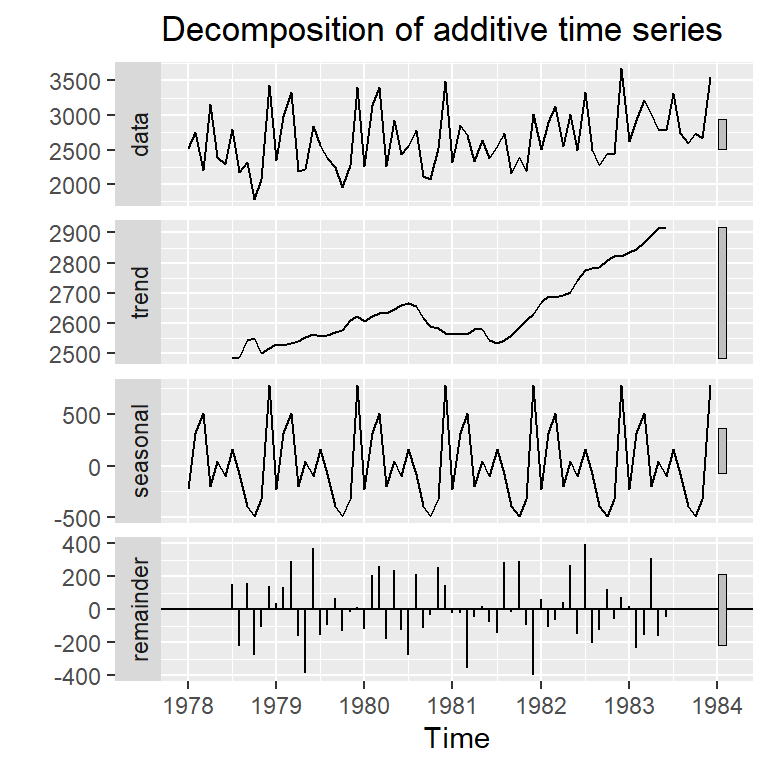
Descomposición multiplicativa
Contenido
Componentes de las series temporales
Medias móviles
Descomposición aditiva
Descomposición multiplicativa
Otras técnicas de descomposición
Descomposición STL
Descomposición y pronóstico
Descomposición multiplicativa
Para descomponer una serie con el modelo multiplicativo:
Paso I : Al igual que la descomposición aditiva, obtener \(MA_t\) que la estimación del componente tendencia-ciclo \(T_t\). Ver diapositiva 15
Paso II: Calcule el cociente \(C_t=\frac{Z_t}{PM_t}\) que es una estimación del producto del componente estacional y el componente irregular, i.e. \(S_t \times I_t\).
Paso III: Para estimar el componente estacional, agrupar los valores \(C_t\), correspondientes a cada estación \(m\) y calcular un promedio para cada estación. De esta forma, obtenemos los índices estacionales: \[S^*_j,~~~j=1,...m.\] Se debe ajustar estos índices para que su producto sea 1 (media geométrica), y así se obtienen los índices estacionales normalizados. \[S_j=\frac{S^*_j}{\bar{S^*_G}}.\]
Paso IV:
Se obtiene la serie ajustada estacionalmente, que son los valores desestacionalizados usando \(d_t=\frac{Z_t}{S_j}\).
Paso V:
Finalmente, se obtiene el residuo \(I_t=\frac{Z_t}{T_t S_j}\).
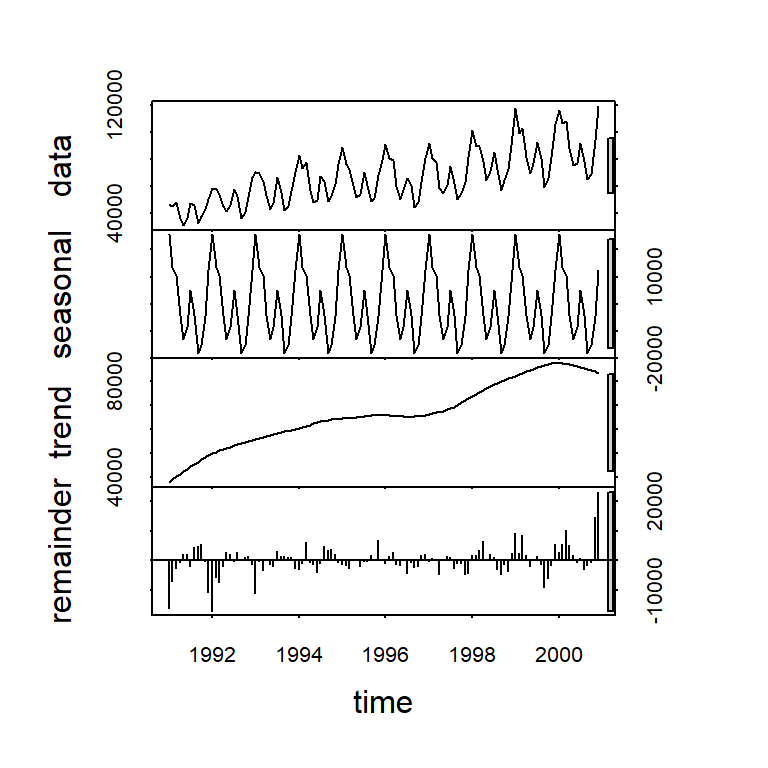
Ejemplo 2.3 de Hernández (2011): serie mensual del número de turistas que ingresaron a Costa Rica de 1991 a 2000.
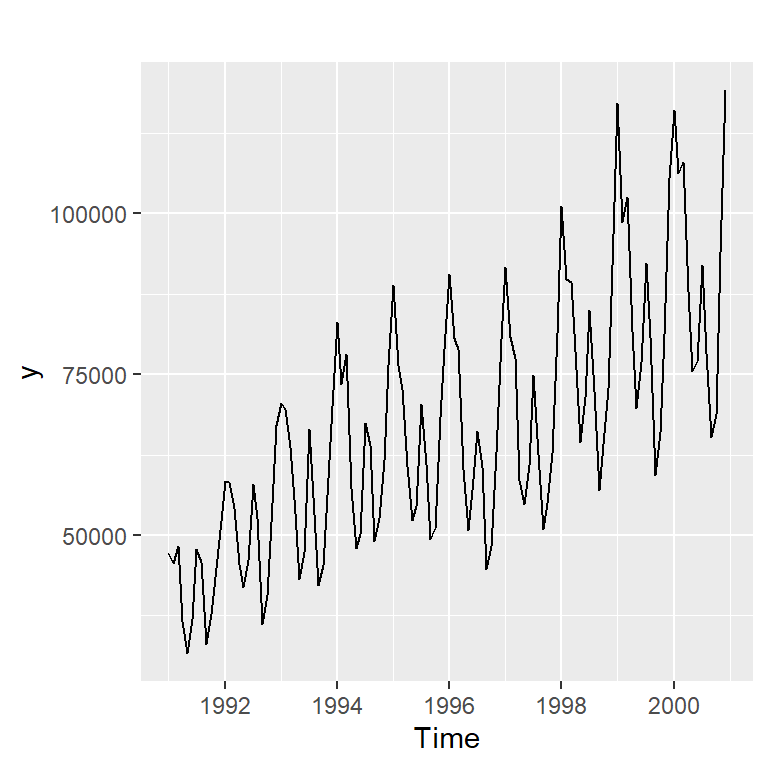
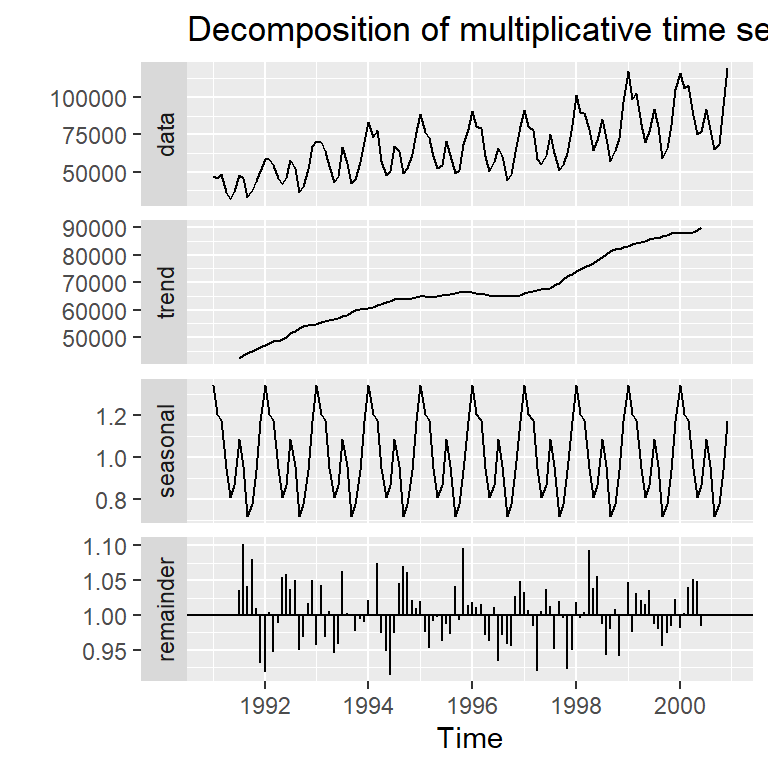
Descomposición Clásica
Nota
- La estimación de la tendencia no se puede realizar para las primeras y últimas observaciones.
- Supone que el componente estacional repite de forma constante (aditiva o multiplicativa) a lo largo del tiempo.
- Ej: la demanda eléctrica puede variar el comportamiento con las nuevas tecnologías como el aire acondicionado.
- La descomposición clásica no es apta para series que presentan variaciones a lo largo del periodo.
Otras técnicas de descomposición
Contenido
Componentes de las series temporales
Medias móviles
Descomposición aditiva
Descomposición multiplicativa
Otras técnicas de descomposición
Descomposición STL
Descomposición y pronóstico
Otras técnicas de descomposición
- Existe una gran variedad de técnicas modificando formas de estimar la tendencia y la estacionalidad. Ej: X11, X11-ARIMA, X12-ARIMA, etc.
- La mayoría de ellas son desarrolladas por las agencias oficiales del censo de EU para realizar descomposición de series oficiales.
- Al igual que la descomposición clásica, son útiles para analizar series mensuales o trimestrales. Sin embargo, para datos diarios u horarios no son útiles (se necesitan otras metodologías).
- Utilizan otros criterios como media móvil ponderada.
Descomposición STL
Contenido
Componentes de las series temporales
Medias móviles
Descomposición aditiva
Descomposición multiplicativa
Otras técnicas de descomposición
Descomposición STL
Descomposición y pronóstico
Descomposición STL
- Propuesto por Cleveland et al. (1990)
- Seasonal and trend descomposition using loess (en inglés).
- LOESS (locally weighted smoothing), también llamado LOWESS (Locally Weighted Scatterplot Smoothing), es una técnica de regresión no lineal.
- Localmente ajusta regresión lineal y crea una curva suave en el tiempo para estimar la tendencia.
- Ventajas:
- el componente estacional puede variar en el tiempo.
- permite el control del grado de suavizamiento.
- es robusto a los outliers.
Descomposición y pronóstico
Contenido
Componentes de las series temporales
Medias móviles
Descomposición aditiva
Descomposición multiplicativa
Otras técnicas de descomposición
Descomposición STL
Descomposición y pronóstico
Descomposición y pronóstico
- Proyectar al futuro con los componentes individuales de la serie.
- El componente tendencia-ciclo se estima con una función simple (línea recta, cuadrática, etc.).
- El componente estacional se estima con el componente estacional del último periodo de los datos.
- El componente irregular se puede proyectar como 0 (modelo aditivo) y como 1 (modelo multiplicativo), si no está correlacionado (ruido blanco).
Evaluación de los pronósticos de un modelo
Sean \(Z_1,...,Z_T\) las observaciones y \(\hat{Z}_1,...,\hat{Z}_T\) los valores ajustados de un modelo particular.
Defina el error de pronóstico \[e_t=Z_t- \hat{Z}_t\] Algunas consideraciones:
¿Son correlacionados?
¿Tienen media cero?
¿Variancia constante?
¿Tienen distribución normal?
Medidas de precisión
Suponga que se tiene una serie \(Z_t\) de \(T\) observaciones.
Dividir las observaciones en \(Z_1,...,Z_{T-1}\) y \(Z_{T}\).
Ajustar el modelo con \(Z_1,...,Z_{T-1}\) y pronosticar el valor de \(\hat{Z}_{T}\).
El error de pronóstico es definido por \[e_T=Z_T- \hat{Z}_T\]
\(\hat{Z}_{T}\) es llamado pronóstico un paso para adelante.
\(e_{T}\) es llamado error de pronóstico un paso para adelante.
En la práctica, se divide la serie \(Z_t\), \(t=1,...,T\) en dos conjuntos:
- Base de datos de entrenamiento \(Z_1,...,Z_{T'}\) (para ajustar el modelo)
- Base de datos de prueba \(Z_{T'+1},...,Z_{T'+h}\) (para validar el modelo)
donde \(1< T'< T\). Usualmente \(h/T \approx 0.2\) o \(0.1\).
- Ajustar el modelo con \(Z_1,...,Z_{T'}\) y pronosticar los valores de \(\hat{Z}_{T'+1},...,\hat{Z}_{T'+h}\) (pronóstico a \(h\) paso para adelante).
- Definan las siguientes medidas:
- Error absoluto medio (mean absolute error, MAE) \[\operatorname{MAE} = \frac{\sum\limits_{i=1}^h |e_{T+i}|}{h}\]
Error cuadrático medio (mean squared error, MSE) \[\operatorname{MSE} = \frac{\sum\limits_{i=1}^h (e_{T+i})^2}{h}\]
Error porcentual absoluto medio (mean absolute percentage error, MAPE) \[\operatorname{MAPE} = \frac{\sum\limits_{i=1}^h |EP_{T+i}|}{h}\] donde \(EP_{j}=100 \left[ \frac{Z_j-\hat{Z_j}}{Z_j} \right]\).