Introducción3
Propiedades de la media y variancia muestral
Sea \(X_{1}, \ldots, X_{n}\) una m.a. cuya distribución poblacional tiene media \(\mu\) y varianza \(\sigma^{2}\). Definan la media muestral y la Varianza muestral:
\[\bar{X}_{n}=\bar {X}=\sum_{i=1}^n \frac{X_i}{n}, ~~~\text{y}~~~ S^{2} = \frac{\sum_{i=1}^n{\left(X_{j}-\bar{X}\right)^2}}{n-1}.\]
Entonces,
- \(E\left(\overline{X}_{n}\right)=\mu\), y \(\operatorname{Var}\left(\bar{X}_{n}\right)=\frac{\sigma^{2}}{n}\)
- \(E\left(S^2\right)=\sigma^2\).
Propiedades de la media muestral
Ley de los grandes números
Suponga que \(X_{1}, \ldots, X_{n}\) es una muestra de una distribución con media \(\mu\) y varianza finita. Sea \(\bar{X}_{n}\) la media muestral. Entonces, \[\begin{equation*} \bar{X}_{n} \stackrel{p}{\longrightarrow} \mu \end{equation*}\]
Teorema del límite central
Si \(X_1,\ldots, X_n\) es una muestra aleatoria de tamaño \(n\), y la distribución tiene media \(\mu\) y varianza \(0<\sigma^2< \infty\). Entonces se cumple que
\[Z_{n} = \frac{\overline{X}_n-\mu}{\frac{\sigma}{\sqrt{n}}} \stackrel{d}{\longrightarrow} N\left(0,1\right) \quad si\quad n \rightarrow \infty\] o lo que es equivalente \[\overline{X}_n \xrightarrow{\text{d}} N\left(\mu, \frac{\sigma^2}{n}\right) \quad si\quad n \rightarrow \infty.\]
Propiedades de la media y variancia muestral (Caso Normal)
Teorema: Si \(\bar{X}_n\) es la media muestral de una muestra aleatoria de tamaño \(n\) de una distribución normal de media \(\mu\) y variancia \(\sigma^2\), entonces \(\bar{X}_n\) tiene una distribución normal con media \(\mu\) y variancia \(\sigma^2/n\), es decir, \(\bar{X}_n \thicksim N(\mu,\sigma^2/n)\)
Aplicación más común: valores de la tabla z (normal estándar).
Ejemplo:
Si \(X\) es una variable aleatoria con distribución normal con media 15 y variancia 16. Se toman muestras aleatorias de tamaño 9. Calcular \(P(12 < \bar{X}_n < 17)\).
\[ P(12 < \bar{X}_n < 17) = P\left(\frac{ 12-15 }{ 4/3 }<Z<\frac{ 17-15 }{ 4/3 }\right)\] \[ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ = P(-2.25 < Z <1.5) = 0.9210\]
Propiedades de la media y variancia muestral (Caso Normal)
Propiedades de la media y variancia muestral (Caso Normal)
Teorema: Si \(X_1, X_2, ..., X_n\) es una muestra aleatoria con distribución normal con media \(\mu\) y variancia \(\sigma^2\), entonces:
- \(\bar{X}\) y \(S^2\) son estocásticamente independientes.
- La variable \(U = \frac{(n-1)S^2}{\sigma^2}\) tiene distribución \(\chi^2\) con \(n-1\) grados de libertad.
- La densidad de \(S^2\) es la densidad gamma.
La prueba de este teorema está fuera de los contenidos de este curso.
Nota: Se puede usar para probar que \(Var(S^2) = \frac{2\sigma^4}{n-1}\) cuando asumimos que \(X_1, X_2, ..., X_n\) es una muestra aleatoria con distribución normal con media \(\mu\) y variancia \(\sigma^2\).
Propiedades de la media y variancia muestral (Caso Normal)
\[E \left ( \frac{(n-1)S^2}{\sigma^2} \right )=n-1\] \[\Rightarrow E \left ( S^2 \right )=\sigma^2.\]
\[Var \left ( \frac{(n-1)S^2}{\sigma^2} \right )= 2(n-1)\] \[\Rightarrow\frac{(n-1)^2}{\sigma^4} \cdot Var(S^2) = 2(n-1)\] \[\Rightarrow Var(S^2) = \frac{2\sigma^4(n-1)}{(n-1)^2}\] \[\Rightarrow Var(S^2) = \frac{2\sigma^4}{n-1}.\]
Propiedades de la media y variancia muestral (Caso Normal)
Teorema: Si \(X_1, X_2, ..., X_n\) es una muestra aleatoria con distribución normal con media \(\mu\) y variancia \(\sigma^2\), entonces la variable aleatoria: \(t = \frac{ (\bar{ X }-\mu) } { S/\sqrt{ n } }\) se distribuye como una \(t\) de Student con \(n-1\) grados de libertad.
Propiedades de la media y variancia muestral (Caso Normal)
Prueba:
Sabemos que \(\frac{\bar{X}-\mu}{\sigma/\sqrt{n}}\) se distribuye como una \(N(0,1)\). Por teorema anterior sabemos que \(U = \frac{(n-1)S^2}{\sigma^2}\sim \chi^2_{n-1}\). Del mismo teorema, sabemos que \(\bar{X}\) y \(S^2\) son independientes, y por los teorema (vistos en la clase de contínuos), sabemos que la definición de una variable \(t\) de Student es \(Y = \frac{N(0,1)}{\sqrt{\chi^2/k}}\).
Por todo lo anterior:
\[ \frac{ \frac{ \bar{X}-\mu } { \sigma/\sqrt{ n } } } { \sqrt{\frac{ \frac{ (n-1)S^2 } { \sigma^2 }}{(n-1)} } }=\frac{ \bar{ X }-\mu } { S/\sqrt{ n } } \]
es una \(t\) de Student con \(n-1\) grados de libertad.
Propiedades de la media y variancia muestral (Caso Normal)
Teorema: Si \(X_1, X_2, ..., X_m\) es una muestra aleatoria con distribución normal con media \(\mu_X\) y variancia \(\sigma^2_X\). Sea \(Y_1, Y_2, ..., Y_n\) es una muestra aleatoria con distribución normal con media \(\mu_Y\) y variancia \(\sigma^2_Y\). Si ambas poblaciones son independientes entonces: \(\frac{S^2_X/\sigma^2_X}{S^2_Y/\sigma^2_Y}\) tiene una distribución \(F_{m-1, n-1}\).
Prueba:
Por teorema sabemos que \(U = \frac{(n-1)S^2}{\sigma^2}\) tiene distribución \(\chi^2\) con \(n-1\) grados de libertad. Usando la definición de la distribución F podemos reescribir la división como la división de dos variables distribuidas como \(\chi^2\) con distintos grados de libertad:
\[ \frac{ \frac{ (m-1)S^2_X } { \sigma^2_X } /(m-1)} { \frac{ (n-1)S^2_Y } { \sigma^2_Y }/(n-1) } = \frac{ S^2_X/\sigma^2_X } { S^2_Y/\sigma^2_Y } \]
Propiedades de la media y variancia muestral (Caso Normal)
Teorema: Si \(X_1, X_2, ..., X_n\) es una muestra aleatoria con distribución normal con media \(\mu_X\) y variancia \(\sigma^2\). Sea \(Y_1, Y_2, ..., Y_m\) es una muestra aleatoria con distribución normal con media \(\mu_Y\) y variancia \(\sigma^2\). Si ambas poblaciones son independientes entonces:
\[ \frac{ (\bar{ X }-\bar{ Y })-(\mu_X-\mu_Y) } { S_p \sqrt{ \frac{1}{n}+\frac{1}{m} } }\]
se distribuye como una \(t\) de Student con \(n+m-2\) grados de libertad, donde
\[ S_p = \sqrt{ \frac{ (n-1)S^2_X+(m-1)S^2_Y } { n+m-2 } }.\]
Propiedades de la media y variancia muestral (Caso Normal)
Prueba:
Se sabe que:
\(\frac{(\bar{X}-\bar{Y})-(\mu_X-\mu_Y)}{\sigma \sqrt{\frac{1}{n}+\frac{1}{m}}} \sim N(0,1)\). Como \(\bar{X} \sim N(\mu_X,\sigma^2/n)\) y \(\bar{Y} \sim N(\mu_Y,\sigma^2/m)\) y por lo tanto, \((\bar{X}-\bar{Y}) \sim N(\mu_X-\mu_Y,\sigma^2/n+\sigma^2/m)\).
Además, \(\frac{(n-1)S^2_X}{\sigma^2}+\frac{(m-1)S^2_Y}{\sigma^2}\) es una \(\chi^2_{(n+m-2)}\) por teorema.
Por definición de una variable \(t\) de student, el cociente entre la \(N(0,1)\) de la parte a) y la raíz cuadrada de la parte b) dividida entre sus grados de libertad, es una \(t\) de student con \(n+m-2\) grados de libertad. Se se calcula el cociente y se simplifica, se obtiene la variable aleatoria del Teorema.
Propiedades de la media y variancia muestral (Caso Normal)
\[\begin{eqnarray*} \frac{\frac{(\bar{X}-\bar{Y})-(\mu_X-\mu_Y)}{\sigma\sqrt{\frac{1}{n}+\frac{1}{m}}}}{\sqrt{\frac{\frac{(n-1)S^2_X+(m-1)S^2_Y}{\sigma^2}}{n+m-2}}} &=& \frac{\frac{(\bar{X}-\bar{Y})-(\mu_X-\mu_Y)}{\sigma\sqrt{\frac{1}{n}+\frac{1}{m}}}}{\frac{1}{\sigma}\sqrt{\frac{(n-1)S^2_X+(m-1)S^2_Y}{n+m-2}}}\\ &=& \frac{(\bar{X}-\bar{Y})-(\mu_X-\mu_Y)}{\sqrt{\frac{(n-1)S^2_X+(m-1)S^2_Y}{n+m-2}}\cdot\sqrt{\frac{1}{n}+\frac{1}{m}}} \\ \\ &=& \frac{(\bar{X}-\bar{Y})-(\mu_X-\mu_Y)}{S_p\sqrt{\frac{1}{n}+\frac{1}{m}}} \end{eqnarray*}\]
Estadísticos de orden
Supongamos que se tiene una muestra aleatoria de tamaño \(n\) de una población infinita que tiene una función de densidad \(f(x)\) y función de distribución \(F(x)\).
Si los valores de estas variables aleatorias se ordenan de manera que al valor más bajo de las \(x\) se le asigna la variable \(X_{(1)}\), al siguiente valor de \(x\) se le asigna la variable \(X_{(2)}\) y de esta forma se continúa hasta que al mayor valor de \(x\) se le asigna la variable \(X_{(n)}\), esto genera un ordenamiento de la muestra aleatoria \(X_1, X_2, ..., X_n\) de manera que \(X_{(1)} < X_{(2)} < ... < X_{(n)}\).
Estas variables denotan los denominados estadísticos de orden. De este análisis surge la siguiente pregunta: ¿Cuál es la distribución del estadístico \(X_{(1)}\)?
Estadísticos de orden
Distribución del mínimo \(X_{(1)}\)
Sean las variables aleatorias \(X_{1},X_{2},...,X_{n}\) independientes e idénticamente distribuidas con función de distribución \(F_X(x)\) y función de densidad \(f_X(x)\). Sea también la variable \(X_{(1)}\) definida por: \(X_{(1)}=\min(X_{1},X_{2},...,X_{n})\), Entonces, la función de distribución del mínimo de la muestra está dada por: \[F_{X_{(1)}}(x)=1-[1-F_X(x)]^{n},\]
y su función de densidad: \[f_{X_{(1)}}(x)=n[1-F_X(x)]^{n-1}f_X(x).\]
Estadísticos de orden
Prueba:
\(F_{X_{(1)}}(x) = P(X_{(1)}\leq x)\)
\(\ \ \ \ \ \ \ \ =P(\min(X_{1},...,X_{n})\leq x)\)
\(\ \ \ \ \ \ \ \ =1-P(\min(X_{1},...,X_{n})>x)\) (Complemento)
\(\ \ \ \ \ \ \ \ =1-P(X_{1}>x,X_{2}>x,...,X_{n}>x)\)
\(\ \ \ \ \ \ \ \ =1-P(X_{1}>x)\cdot P(X_{2}>x) \cdots P(X_{n}>x)\) (Independencia)
\(\ \ \ \ \ \ \ \ =1-[P(X_{1}>x)]^{n}\) (Distribución idéntica)
\(\ \ \ \ \ \ \ \ =1-[1-F_X(x)]^{n}\)
Del mismo modo, la función de densidad de \(X_{(1)}\) sería:
\(f_{X_{(1)}}(x)=F_{X_{(1)}}(x)'=(1-[1-F_X(x)]^{n})'= n[1-F_X(x)]^{n-1}f_X(x)\)
Estadísticos de orden
Distribución del máximo \(X_{(n)}\)
Sean las variables aleatorias \(X_{1},X_{2},...,X_{n}\) independientes e idénticamente distribuidas con función de distribución \(F_X(x)\) y función de densidad \(f_X(x)\). Sea también la variable \(X_{(n)}\) definida por: \(X_{(n)}=\max(X_{1},X_{2},...,X_{n})\), Entonces, la función de distribución del máximo de la muestra está dada por: \[F_{X_{(n)}}(x)=[F_X(x)]^{n},\] y su función de densidad: \[f_{X_{(n)}}(x)=n[F_X(x)]^{n-1}f_X(x).\]
Estadísticos de orden
Distribución del máximo \(X_{(n)}\)
\(F_{X_{(n)}}(x) = P(X_{(n)}\leq x)\)
\(\ \ \ \ \ \ \ \ =P(\max(X_{1},...,X_{n})\leq x)\)
\(\ \ \ \ \ \ \ \ =P(X_{1}\leq x,X_{2}\leq x,...,X_{n}\leq x)\)
\(\ \ \ \ \ \ \ \ =P(X_{1}\leq x)\cdot P(X_{2}\leq x) \cdots P(X_{n}\leq x)\) (Independencia)
\(\ \ \ \ \ \ \ \ =[P(X_{1}\leq x)]^{n}\) (Distribución idéntica)
\(\ \ \ \ \ \ \ \ =[F_{X}(x)]^{n}\)
Del mismo modo, la función de densidad de \(X_{(n)}\) sería:
\(f_{X_{(n)}}(x)=F_{X_{(n)}}(x)'=([F_X(x)]^{n})'= n[F_X(x)]^{n-1}f_X(x)\)
Estadísticos de orden
Teorema: Sea \(X_1, X_2, ..., X_n\) una muestra aleatoria de una población infinita con función de densidad \(f_X(x)\) y función de distribución \(F_X(x)\). Si \(X_{(k)}\) representa el \(k\)-ésimo estadístico de orden, entonces la función de densidad viene dada por:
\[f_{X_{(k)}}(x)= \frac{ n! } { (k-1)!(n-k)! }[F_X(x)]^{ k-1 }[1-F_X(x)]^{ n-k }f_X(x)\]
Nota:
En particular se tiene que \(X_{(1)} = \min\{X_1, X_2, ..., X_n\}\) y \(X_{(n)} = \max\{X_1, X_2, ..., X_n\}\). Además si \(n = 2m + 1\), la mediana de la muestra corresponde al estadístico de orden \(X_{(m+1)}\). Si \(n=2m\), la mediana es \(\frac{1}{2}(X_{m}+X_{m+1})\).
Teorema: Para \(n\) grande, la distribución de muestreo de la mediana para muestras aleatorias de tamaño \(2n + 1\) es aproximadamente normal con media \(\mu\) (mediana poblacional) y variancia \(\frac{1}{8n[f(\mu)]^2}\).
Propiedades deseadas de un “buen” estimador
- ¿Cuáles son las propiedades deseadas de un buen estimador?
Básicamente se resume en la esperanza y la variancia del estimador.
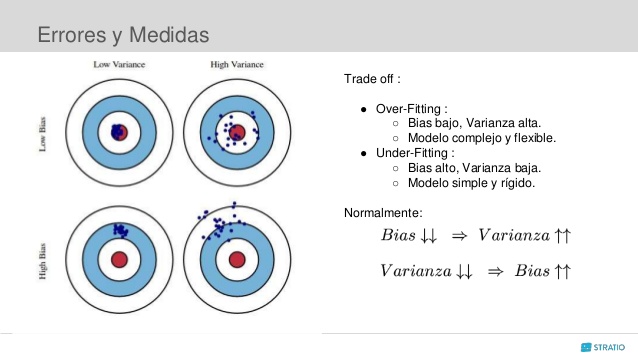
Figura 1. Sesgo y Variancia. Fuente: https://www.slideshare.net/Stratio/lunchlearn-combinacin-de-modelos
Lab01
Ejercicios
- Se desea estimar la media \(\mu\) de una variable aleatoria \(X\). Para ello se toman \(10\) datos y se calcula su media muestral \(\bar{X}\) y la varianza de dichos datos \(\sigma^2_X\). Comente si son verdaderas o falsas las siguientes afirmaciones:
- Por el teorema central del límite sabemos que \(\mu\) será una variable aleatoria normal.
- La media muestral con un conjunto de datos es un número y no una variable aleatoria.
- La media muestral \(\bar{X}\) tiene siempre una distribución muestral normal.
- Para disminuir la varianza de \(\bar{X}\) a la mitad habría que tomar al menos 100 datos.
- Como la media muestral es un estimador insesgado, tenemos asegurado que \(\bar{X} = \mu\)
Ejercicios
