set.seed(100)
gen_ar1 <- function(N = 150, phi1 = 0.8, sigma2 = 1) {
a <- rnorm(N,0,sqrt(sigma2))
y <- as.numeric(0)
y[1] <- a[1]
for(i in 2:N){
y[i] <- phi1*y[i-1]+a[i]
}
return(y)
}Lista de ejercicios 4
Un estudio de simulaciones del proceso AR(1)
El objetivo de esta práctica es entender los conceptos de estacionariedad de los modelos autorregresivos de orden \(1\), AR(1), mediante simulaciones, con el fin de complementar el aprendizaje de los conceptos teóricos vistos en la clase.
Considere el proceso AR(1) que está definido por el siguiente proceso estocástico lineal: \[Y_t=C+\phi_1 Y_{t-1}+a_t\] donde \(C\) y \(\phi_1\) son constantes desconocidas, y \(a_t \sim wn(0,\sigma_a^2)\). Además, recuerde que el proceso AR(1) es estacionario si \(|\phi_1|<1\).
Ejercicio 4.1 Defina primero una semilla y una función para generar un proceso AR(1) con \(C=0\) en donde \(a_t \sim N(0,\sigma_a^2)\), usando el siguiente código:
Discuta y explique en sus palabras el significado de cada línea de códigos.
Ejercicio 4.2 Genere \(10\) veces un proceso AR(1) con errores como ruido blanco guassiano de longitud \(150\) observaciones con \(\phi_1=0.8\) y \(\sigma_a^2=1\).
realizaciones1 <- replicate(n = 10 ,gen_ar1(N=150,phi1=0.8,sigma2=1), simplify = "array" )Ejercicio 4.3 Ahora en cada una de sus computadoras, grafique estas 10 realizaciones de un AR(1) usando:
ts.plot(realizaciones1,col=1:10)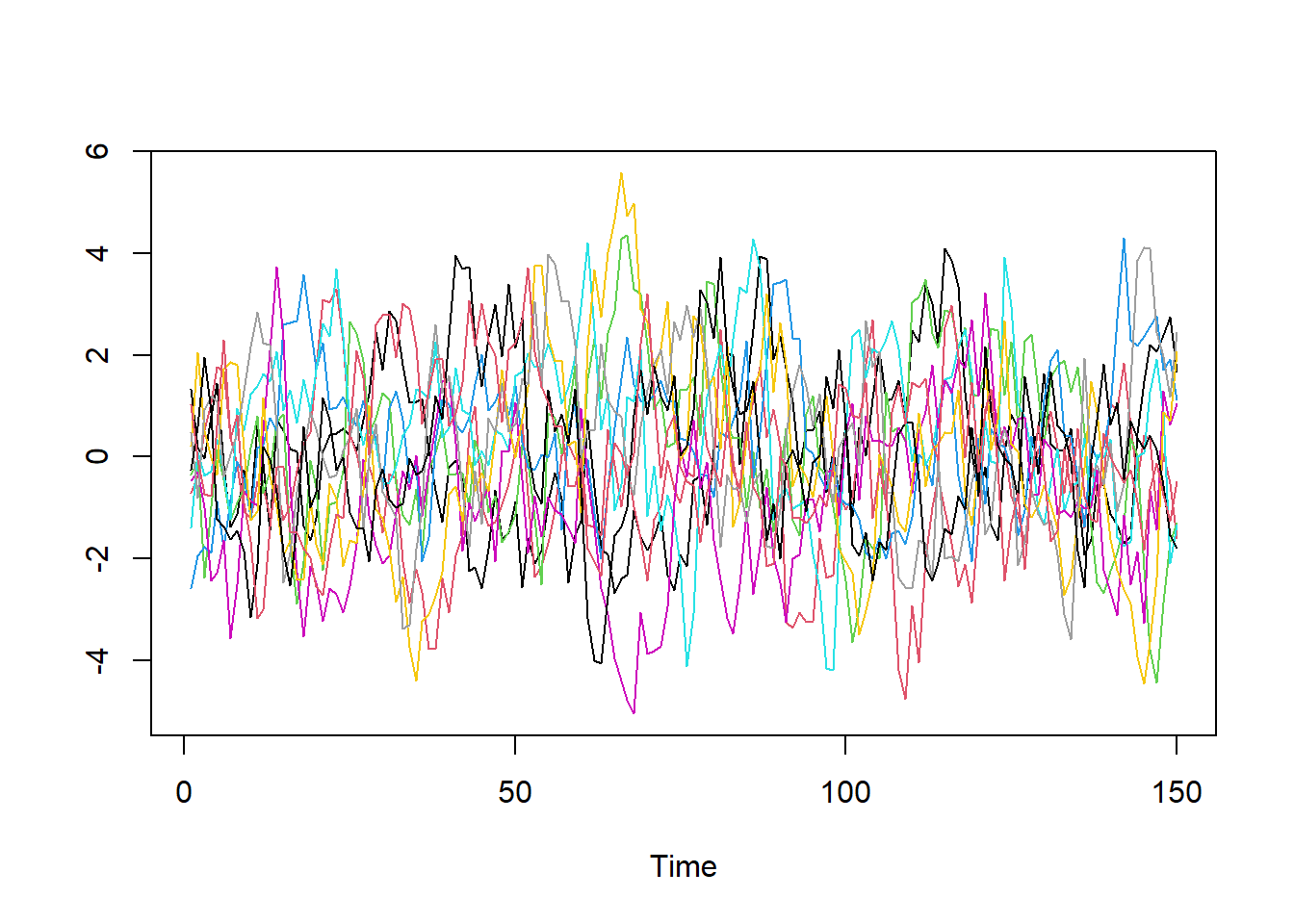
Comenten y discutan las características de estas realizaciones en el gráfico.
Ejercicio 4.4 En vez de \(10\) simulaciones, genere \(500\) veces el proceso AR(1) con errores como ruido blanco guassiano de longitud \(150\) observaciones con \(\phi_1=0.8\) y \(\sigma_a^2=1\).
realizaciones2 <- replicate(n = 500 ,gen_ar1(N=150,phi1=0.8,sigma2=1), simplify = "array" )Calcule la media y la variancia de las \(500\) realizaciones del proceso usando:
promedios <- apply(realizaciones2,MARGIN=2,mean)
variancias <- apply(realizaciones2,MARGIN=2,var)Recuerde que la media del proceso es \(E(Z_t)=C \left( \frac{1}{1-\phi_1}\right)=\mu\) y la variancia es \(Var(Y_t)=\left( \frac{1}{1-\phi_1^2} \right) \sigma_a^2\). Haga un análisis exploratorio con las 500 medias y variancias muestrales con medidas descriptivas e histogramas. Compárelos con la media y la variancia teórica del proceso y comente el resultado. ¿La estimación es buena?
Ejercicio 4.5 Extrae las primeras dos realizaciones de los datos generados y calcule la función de autocorrelación muestral y función de autocorrelación parcial muestral.
y1 <- realizaciones2[,1]
astsa::acf2(y1)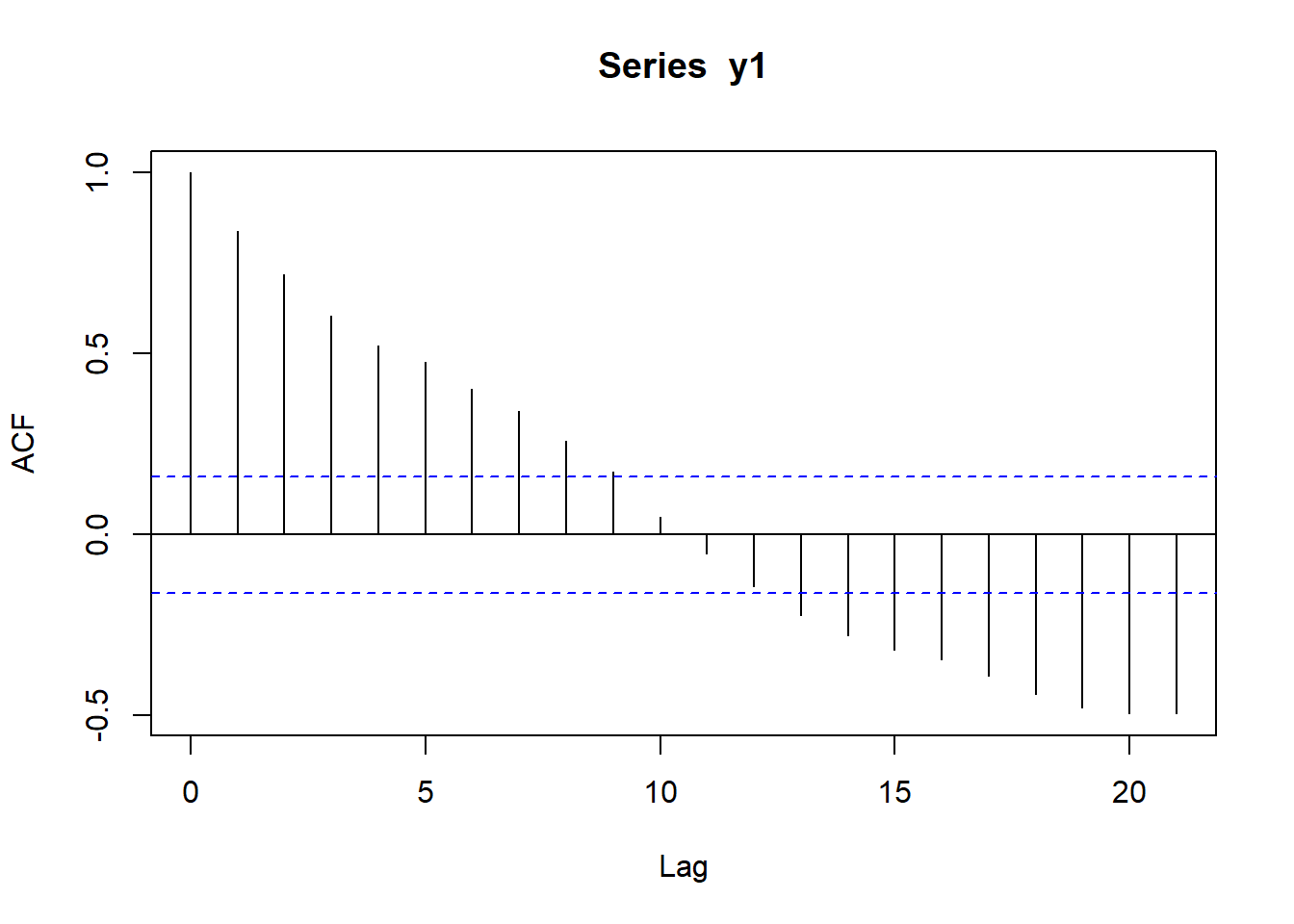
y2 <- realizaciones2[,2]
astsa::acf2(y2)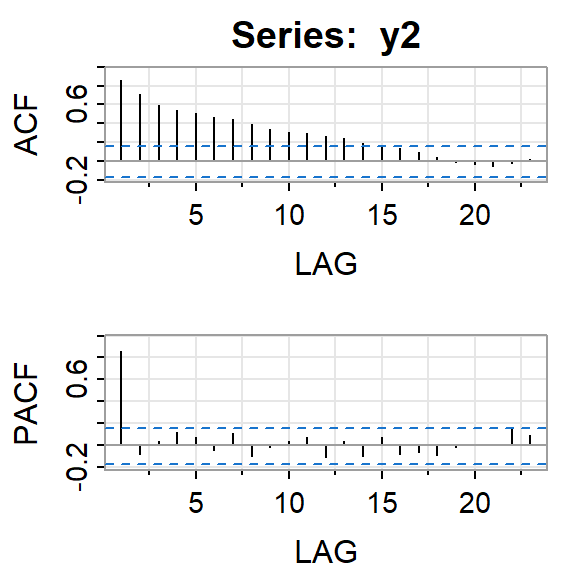
Comente los resultados y compárelos con la función de autocorrelación y autocorrelación parcial teóricas.
Ejercicio 4.6 Repita el Ejercicio 4.1 al Ejercicio 4.5 pero con \(\phi_1=1\), es decir, el proceso generado no cumple la condición de estacionariedad. Compare los resultados con los ejercicios anteriores.
Ejercicio 4.7 Utilice una serie generada en Ejercicio 4.6, llámese \(Y_t\), y obtenga la serie diferenciada de la serie \(Y_t\) definida como \[Z_t = \Delta Y_t=Y_t-Y_{t-1}.\] Analice el gráfico lineal de \(Z_t = \Delta Y_t\), así como la función de autocorrelación y la parcial muestrales.
Ejercicio 4.8 Repita el Ejercicio 4.6 y el Ejercicio 4.7 pero con \(\phi_1=1.3\). Comente los resultados.
Ejercicio 4.9 Note que la función gen_ar1 genera la primera observación de la serie, \(Y_t\) como \(Y_1 \sim N(0,\sigma^2)\). Esto implica que \(Y_1\) no es autorregresivo de orden 1. Proponga una forma de corregir este problema y repita el Ejercicio 4.1 al Ejercicio 4.5. ¿Qué diferencia nota?